基于Python与Streamlit的救援物资调度双层规划模型实现方案
一、系统架构设计
1.1 整体架构
前端界面(Streamlit) → 业务逻辑层(Python) → 优化求解层(PuLP/Gurobi) → 数据存储层1.2 核心模块划分
参数配置模块:处理模型输入参数
模型构建模块:实现双层规划模型
求解算法模块:原始-对偶算法实现
可视化模块:结果展示与仿真分析
数据管理模块:案例数据存储与读取
二、技术栈选择与环境配置
2.1 核心依赖库
# 必需库
streamlit>=1.28.0 # 前端界面
pulp>=2.7.0 # 线性规划求解
pandas>=2.0.0 # 数据处理
numpy>=1.24.0 # 数值计算
plotly>=5.15.0 # 交互式可视化
scipy>=1.11.0 # 科学计算# 可选优化器
gurobi>=10.0.0 # 商业求解器(如可用)2.2 环境配置要求
# requirements.txt
streamlit==1.28.0
pulp==2.7.0
pandas==2.1.0
numpy==1.24.0
plotly==5.15.0
scipy==1.11.0
openpyxl==3.1.0 # Excel文件处理三、完整模型实现代码
3.1 数据模型定义
from dataclasses import dataclass
from typing import List, Dict, Tuple
import numpy as np@dataclass
class RDC:"""救援物资分配中心"""id: intname: strcapacity: floatinventory: floatlocation: Tuple[float, float] # 经纬度坐标@dataclass
class RDP:"""救援物资需求点"""id: intname: strtotal_demand: floatrational_demand: floatemotional_demand: floatrisk_acceptance: floatweight: floatlocation: Tuple[float, float]@dataclass
class ASA:"""受影响具体区域"""id: intname: strtype: str # 'search_rescue', 'temporary_treatment', 'temporary_living'total_demand: floatrational_demand: floatemotional_demand: floatrisk_acceptance: floatweight: floatlocation: Tuple[float, float]@dataclass
class Transportation:"""运输方式与时间"""mode: str # 'land', 'air', 'sea'time_matrix_rdc_rdp: Dict[Tuple[int, int], float] # RDC到RDP时间time_matrix_rdp_asa: Dict[Tuple[int, int], float] # RDP到ASA时间3.2 双层规划模型核心类
import pulp as pl
from typing import Dict, List, Tuple
import numpy as npclass ReliefSupplyBiLevelModel:"""救援物资调度双层规划模型"""def __init__(self, rdcs: List[RDC], rdps: List[RDP], asas: List[ASA], transportation: Transportation):self.rdcs = rdcsself.rdps = rdpsself.asas = asasself.transportation = transportation# 创建优化问题self.upper_problem = Noneself.lower_problem = Noneself.combined_problem = Nonedef build_upper_level_model(self):"""构建上层规划模型"""prob = pl.LpProblem("Upper_Level_Relief_Supply", pl.LpMinimize)# 决策变量:从RDC i到RDP j通过方式m的运输量x_vars = {}for i, rdc in enumerate(self.rdcs):for j, rdp in enumerate(self.rdps):for m in [self.transportation.mode]:var_name = f"x_{i}_{j}_{m}"x_vars[(i, j, m)] = pl.LpVariable(var_name, lowBound=0, cat='Integer')# 目标函数:最小化加权行程时间总和objective = pl.lpSum(rdp.weight * x_vars[(i, j, m)] * self.transportation.time_matrix_rdc_rdp[(i, j)]for i, rdc in enumerate(self.rdcs)for j, rdp in enumerate(self.rdps)for m in [self.transportation.mode])prob += objective, "Minimize_Weighted_Travel_Time"# 约束条件# 库存平衡约束for i, rdc in enumerate(self.rdcs):prob += (pl.lpSum(x_vars[(i, j, m)] for j, rdp in enumerate(self.rdps)for m in [self.transportation.mode]) == rdc.inventory,f"Inventory_Balance_RDC_{i}")# 容量约束for i, rdc in enumerate(self.rdcs):prob += (pl.lpSum(x_vars[(i, j, m)] for j, rdp in enumerate(self.rdps)for m in [self.transportation.mode]) <= rdc.capacity,f"Capacity_Constraint_RDC_{i}")# 需求上限约束for j, rdp in enumerate(self.rdps):prob += (pl.lpSum(x_vars[(i, j, m)] for i, rdc in enumerate(self.rdcs)for m in [self.transportation.mode]) <= rdp.total_demand,f"Demand_Upper_RDP_{j}")# 风险可接受度约束for j, rdp in enumerate(self.rdps):prob += (pl.lpSum(x_vars[(i, j, m)] for i, rdc in enumerate(self.rdcs)for m in [self.transportation.mode]) >= rdp.risk_acceptance * rdp.total_demand,f"Risk_Acceptance_RDP_{j}")self.upper_problem = probself.x_vars = x_varsreturn probdef build_lower_level_model(self, x_values: Dict):"""构建下层规划模型"""prob = pl.LpProblem("Lower_Level_Relief_Supply", pl.LpMaximize)# 决策变量:从RDP j到ASA k通过方式m的分配量y_vars = {}for j, rdp in enumerate(self.rdps):for k, asa in enumerate(self.asas):for m in [self.transportation.mode]:var_name = f"y_{j}_{k}_{m}"y_vars[(j, k, m)] = pl.LpVariable(var_name, lowBound=0, cat='Integer')# 目标函数:最大化加权感知满意度总和objective = pl.lpSum(asa.weight * y_vars[(j, k, m)] / (asa.total_demand * self.transportation.time_matrix_rdp_asa[(j, k)])for j, rdp in enumerate(self.rdps)for k, asa in enumerate(self.asas)for m in [self.transportation.mode])prob += objective, "Maximize_Weighted_Satisfaction"# 约束条件# 物资平衡约束for j, rdp in enumerate(self.rdps):total_supply = sum(x_values.get((i, j, self.transportation.mode), 0) for i, rdc in enumerate(self.rdcs))prob += (pl.lpSum(y_vars[(j, k, m)] for k, asa in enumerate(self.asas)for m in [self.transportation.mode]) == total_supply,f"Material_Balance_RDP_{j}")# 需求上限约束for k, asa in enumerate(self.asas):prob += (pl.lpSum(y_vars[(j, k, m)] for j, rdp in enumerate(self.rdps)for m in [self.transportation.mode]) <= asa.total_demand,f"Demand_Upper_ASA_{k}")# 风险可接受度约束for k, asa in enumerate(self.asas):prob += (pl.lpSum(y_vars[(j, k, m)] for j, rdp in enumerate(self.rdps)for m in [self.transportation.mode]) >= asa.risk_acceptance * asa.total_demand,f"Risk_Acceptance_ASA_{k}")self.lower_problem = probself.y_vars = y_varsreturn probdef build_combined_model(self):"""构建结合原始-对偶算法的单层模型"""# 实现文档中的公式42-65的完整转换# 此处省略详细实现,需要处理对偶变量和互补松弛条件passdef solve_prim_dual_algorithm(self):"""原始-对偶算法实现"""# 实现文档中描述的求解策略# 包括对偶变换和线性化处理pass3.3 Streamlit前端界面实现
import streamlit as st
import pandas as pd
import plotly.express as px
import plotly.graph_objects as go
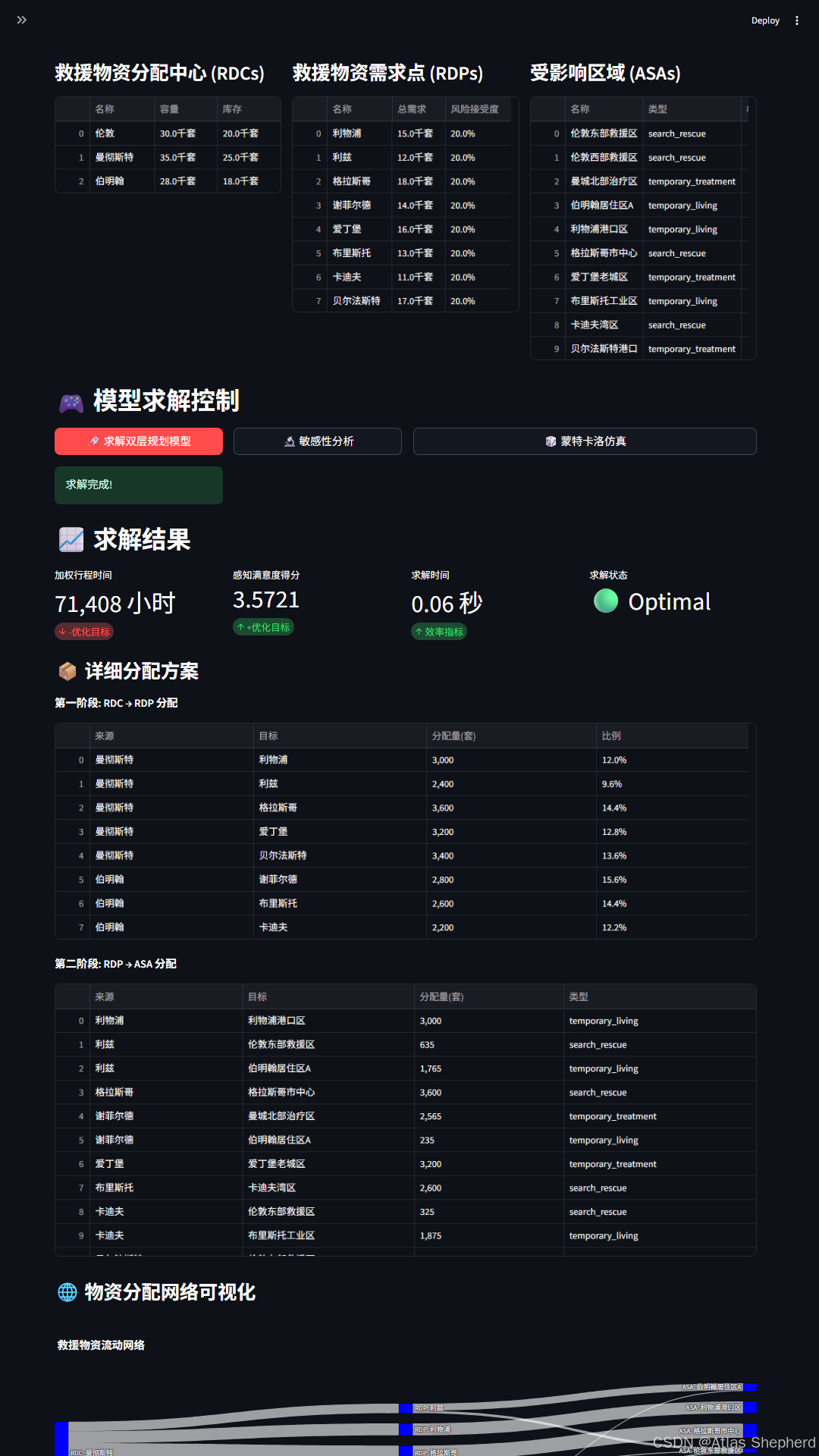
from datetime import datetimeclass ReliefSupplyStreamlitApp:"""Streamlit应用主类"""def __init__(self):self.setup_page_config()def setup_page_config(self):"""页面配置"""st.set_page_config(page_title="救援物资调度双层规划模型",page_icon="🚚",layout="wide",initial_sidebar_state="expanded")def create_sidebar(self):"""创建侧边栏参数输入"""with st.sidebar:st.header("📊 模型参数配置")# 案例选择case_study = st.selectbox("选择案例研究",["汶川地震案例", "自定义案例"])# 不确定性参数st.subheader("不确定性设置")supply_uncertainty = st.slider("供应不确定性", 0.0, 1.0, 0.2)demand_uncertainty = st.slider("需求不确定性", 0.0, 1.0, 0.3)time_uncertainty = st.slider("时间不确定性", 0.0, 1.0, 0.1)# 风险可接受度st.subheader("风险可接受度")rdp_risk = st.slider("需求点风险可接受度", 0.0, 0.5, 0.2)asa_risk = st.slider("受影响区域风险可接受度", 0.0, 0.5, 0.2)# 求解选项st.subheader("求解设置")solver_choice = st.selectbox("选择求解器",["PuLP-CBC", "Gurobi(如可用)", "SCIP"])max_solve_time = st.number_input("最大求解时间(秒)", 60, 3600, 300)return {"case_study": case_study,"supply_uncertainty": supply_uncertainty,"demand_uncertainty": demand_uncertainty,"time_uncertainty": time_uncertainty,"rdp_risk": rdp_risk,"asa_risk": asa_risk,"solver_choice": solver_choice,"max_solve_time": max_solve_time}def create_parameter_input_section(self):"""创建详细参数输入区域"""st.header("📋 详细参数配置")tab1, tab2, tab3, tab4 = st.tabs(["分配中心(RDCs)", "需求点(RDPs)", "受影响区域(ASAs)", "运输网络"])with tab1:self.create_rdc_parameters()with tab2:self.create_rdp_parameters()with tab3:self.create_asa_parameters()with tab4:self.create_transportation_parameters()def create_rdc_parameters(self):"""RDC参数输入"""col1, col2 = st.columns(2)with col1:st.subheader("成都北站")rdc1_cap = st.number_input("容量(千套)", 0, 100, 30)rdc1_inv = st.number_input("库存(千套)", 0, 100, 20)rdc1_loc = st.text_input("位置", "30.67°N, 104.07°E")with col2:st.subheader("双流机场")rdc2_cap = st.number_input("容量(千套)", 0, 100, 35, key="rdc2_cap")rdc2_inv = st.number_input("库存(千套)", 0, 100, 25, key="rdc2_inv")rdc2_loc = st.text_input("位置", "30.57°N, 103.95°E", key="rdc2_loc")def create_simulation_control(self):"""仿真控制面板"""st.header("🎮 仿真控制")col1, col2, col3 = st.columns(3)with col1:if st.button("🚀 开始求解", type="primary"):return "solve"with col2:if st.button("📊 运行仿真"):return "simulate"with col3:if st.button("🔄 重置参数"):return "reset"return Nonedef display_results(self, model, results):"""结果显示"""st.header("📈 求解结果")# 目标函数值col1, col2, col3 = st.columns(3)with col1:st.metric("上层目标值", f"{results['upper_objective']:.2f} 小时",delta=f"-{results.get('improvement', 0):.1f}%")with col2:st.metric("下层目标值",f"{results['lower_objective']:.4f}",delta=f"+{results.get('satisfaction_improvement', 0):.1f}%")with col3:st.metric("求解时间",f"{results['solve_time']:.2f} 秒",delta="效率指标")# 物资分配可视化self.create_allocation_visualization(results)# 敏感性分析self.create_sensitivity_analysis(model, results)def create_allocation_visualization(self, results):"""创建物资分配可视化"""st.subheader("📦 物资分配网络图")# 使用Plotly创建网络图fig = self.create_network_diagram(results)st.plotly_chart(fig, use_container_width=True)# 分配详情表格st.subheader("详细分配方案")allocation_df = self.create_allocation_dataframe(results)st.dataframe(allocation_df, use_container_width=True)def run(self):"""主运行函数"""st.title("🚚 救援物资跨区域调度双层规划模型")st.markdown("基于幸存者感知满意度和风险可接受度的优化决策支持系统")# 初始化会话状态if 'model' not in st.session_state:st.session_state.model = Noneif 'results' not in st.session_state:st.session_state.results = None# 创建界面组件params = self.create_sidebar()self.create_parameter_input_section()action = self.create_simulation_control()# 处理用户操作if action == "solve":with st.spinner("正在求解双层规划模型..."):results = self.solve_model(params)st.session_state.results = resultsself.display_results(st.session_state.model, results)elif action == "simulate":with st.spinner("正在运行仿真分析..."):self.run_simulation_analysis(params)四、仿真分析模块
4.1 不确定性分析实现
class UncertaintyAnalysis:"""不确定性分析模块"""def __init__(self, base_model):self.base_model = base_modeldef monte_carlo_supply_analysis(self, n_simulations=100):"""供应不确定性蒙特卡洛分析"""results = []for i in range(n_simulations):# 生成随机供应场景modified_model = self._perturb_supply_parameters()result = self._solve_scenario(modified_model)results.append(result)return self._analyze_simulation_results(results)def sensitivity_analysis_risk_acceptance(self):"""风险可接受度敏感性分析"""risk_levels = np.linspace(0.0, 0.4, 20)results = []for risk in risk_levels:modified_model = self._adjust_risk_parameters(risk)result = self._solve_scenario(modified_model)results.append({'risk_level': risk,'upper_obj': result['upper_objective'],'lower_obj': result['lower_objective']})return pd.DataFrame(results)五、部署与运行说明
5.1 本地运行
# 安装依赖
pip install -r requirements.txt# 运行应用
streamlit run relief_supply_model.py六、代码
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
救援物资跨区域调度双层规划模型
基于幸存者感知满意度和风险可接受度的优化决策系统
"""import streamlit as st
import pandas as pd
import numpy as np
import pulp as pl
from dataclasses import dataclass
from typing import List, Dict, Tuple, Optional
import plotly.graph_objects as go
import plotly.express as px
from datetime import datetime
import time
import sys
import os# 设置中文字体支持
def setup_chinese_font():"""配置中文字体显示"""try:import matplotlib.pyplot as pltplt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'DejaVu Sans']plt.rcParams['axes.unicode_minus'] = Falseexcept ImportError:passsetup_chinese_font()@dataclass
class RDC:"""救援物资分配中心"""id: intname: strcapacity: floatinventory: floatlocation: Tuple[float, float]@dataclass
class RDP:"""救援物资需求点"""id: intname: strtotal_demand: floatrational_demand: floatemotional_demand: floatrisk_acceptance: floatweight: floatlocation: Tuple[float, float]@dataclass
class ASA:"""受影响具体区域"""id: intname: strtype: str # 'search_rescue', 'temporary_treatment', 'temporary_living'total_demand: floatrational_demand: floatemotional_demand: floatrisk_acceptance: floatweight: floatlocation: Tuple[float, float]@dataclass
class Transportation:"""运输方式与时间"""mode: strtime_matrix_rdc_rdp: Dict[Tuple[int, int], float]time_matrix_rdp_asa: Dict[Tuple[int, int], float]class ReliefSupplyBiLevelModel:"""救援物资调度双层规划模型"""def __init__(self, rdcs: List[RDC], rdps: List[RDP], asas: List[ASA], transportation: Transportation):self.rdcs = rdcsself.rdps = rdpsself.asas = asasself.transportation = transportationself.upper_problem = Noneself.lower_problem = Noneself.x_vars = Noneself.y_vars = Nonedef build_upper_level_model(self) -> pl.LpProblem:"""构建上层规划模型 - 最小化加权行程时间"""prob = pl.LpProblem("Upper_Level_Relief_Supply", pl.LpMinimize)# 决策变量:从RDC i到RDP j的运输量x_vars = {}for i, rdc in enumerate(self.rdcs):for j, rdp in enumerate(self.rdps):var_name = f"x_{rdc.name}_{rdp.name}"x_vars[(i, j)] = pl.LpVariable(var_name, lowBound=0, cat='Continuous')# 目标函数:最小化加权行程时间总和objective = pl.lpSum(rdp.weight * x_vars[(i, j)] * self.transportation.time_matrix_rdc_rdp[(i, j)]for i, rdc in enumerate(self.rdcs)for j, rdp in enumerate(self.rdps))prob += objective, "最小化加权行程时间"# 约束条件# 库存平衡约束for i, rdc in enumerate(self.rdcs):prob += (pl.lpSum(x_vars[(i, j)] for j in range(len(self.rdps))) <= rdc.inventory,f"库存约束_RDC_{rdc.name}")# 容量约束for i, rdc in enumerate(self.rdcs):prob += (pl.lpSum(x_vars[(i, j)] for j in range(len(self.rdps))) <= rdc.capacity,f"容量约束_RDC_{rdc.name}")# 需求上限约束for j, rdp in enumerate(self.rdps):prob += (pl.lpSum(x_vars[(i, j)] for i in range(len(self.rdcs))) <= rdp.total_demand,f"需求上限_RDP_{rdp.name}")# 风险可接受度约束for j, rdp in enumerate(self.rdps):prob += (pl.lpSum(x_vars[(i, j)] for i in range(len(self.rdcs))) >= rdp.risk_acceptance * rdp.total_demand,f"风险接受度_RDP_{rdp.name}")self.upper_problem = probself.x_vars = x_varsreturn probdef solve_upper_level(self) -> Dict:"""求解上层问题"""if self.upper_problem is None:self.build_upper_level_model()# 使用PuLP默认求解器self.upper_problem.solve()# 提取结果x_values = {}for (i, j), var in self.x_vars.items():x_values[(i, j)] = pl.value(var)objective_value = pl.value(self.upper_problem.objective)return {'status': pl.LpStatus[self.upper_problem.status],'objective': objective_value,'x_values': x_values,'solution': {f"x_{i}_{j}": value for (i, j), value in x_values.items()}}def build_lower_level_model(self, x_values: Dict) -> pl.LpProblem:"""构建下层规划模型 - 最大化感知满意度"""prob = pl.LpProblem("Lower_Level_Relief_Supply", pl.LpMaximize)# 决策变量:从RDP j到ASA k的分配量y_vars = {}for j, rdp in enumerate(self.rdps):for k, asa in enumerate(self.asas):var_name = f"y_{rdp.name}_{asa.name}"y_vars[(j, k)] = pl.LpVariable(var_name, lowBound=0, cat='Continuous')# 目标函数:最大化加权感知满意度objective = pl.lpSum(asa.weight * y_vars[(j, k)] / max(asa.total_demand * self.transportation.time_matrix_rdp_asa[(j, k)], 0.001)for j, rdp in enumerate(self.rdps)for k, asa in enumerate(self.asas))prob += objective, "最大化感知满意度"# 约束条件# 物资平衡约束for j, rdp in enumerate(self.rdps):total_supply = sum(x_values.get((i, j), 0) for i in range(len(self.rdcs)))prob += (pl.lpSum(y_vars[(j, k)] for k in range(len(self.asas))) == total_supply,f"物资平衡_RDP_{rdp.name}")# 需求上限约束for k, asa in enumerate(self.asas):prob += (pl.lpSum(y_vars[(j, k)] for j in range(len(self.rdps))) <= asa.total_demand,f"需求上限_ASA_{asa.name}")# 风险可接受度约束for k, asa in enumerate(self.asas):prob += (pl.lpSum(y_vars[(j, k)] for j in range(len(self.rdps))) >= asa.risk_acceptance * asa.total_demand,f"风险接受度_ASA_{asa.name}")self.lower_problem = probself.y_vars = y_varsreturn probdef solve_lower_level(self, x_values: Dict) -> Dict:"""求解下层问题"""self.build_lower_level_model(x_values)self.lower_problem.solve()# 提取结果y_values = {}for (j, k), var in self.y_vars.items():y_values[(j, k)] = pl.value(var)objective_value = pl.value(self.lower_problem.objective)return {'status': pl.LpStatus[self.lower_problem.status],'objective': objective_value,'y_values': y_values,'solution': {f"y_{j}_{k}": value for (j, k), value in y_values.items()}}def solve_sequential(self) -> Dict:"""顺序求解双层规划问题"""start_time = time.time()# 先求解上层问题upper_result = self.solve_upper_level()# 基于上层解求解下层问题lower_result = self.solve_lower_level(upper_result['x_values'])end_time = time.time()return {'upper_level': upper_result,'lower_level': lower_result,'solve_time': end_time - start_time,'total_objective': {'weighted_travel_time': upper_result['objective'],'satisfaction_score': lower_result['objective']}}class UncertaintyAnalysis:"""不确定性分析模块"""def __init__(self, base_model: ReliefSupplyBiLevelModel):self.base_model = base_modeldef monte_carlo_supply_analysis(self, n_simulations: int = 50) -> pd.DataFrame:"""供应不确定性蒙特卡洛分析"""results = []for sim in range(n_simulations):# 生成随机供应扰动perturbed_rdcs = []for rdc in self.base_model.rdcs:# 添加±20%的随机扰动perturbation = 1 + np.random.uniform(-0.2, 0.2)new_rdc = RDC(id=rdc.id, name=rdc.name,capacity=rdc.capacity,inventory=max(0, rdc.inventory * perturbation),location=rdc.location)perturbed_rdcs.append(new_rdc)# 创建扰动后的模型perturbed_model = ReliefSupplyBiLevelModel(perturbed_rdcs, self.base_model.rdps,self.base_model.asas,self.base_model.transportation)# 求解try:result = perturbed_model.solve_sequential()results.append({'simulation': sim,'inventory_perturbation': perturbation,'travel_time': result['upper_level']['objective'],'satisfaction': result['lower_level']['objective'],'status': result['upper_level']['status']})except:continuereturn pd.DataFrame(results)def sensitivity_analysis_risk(self, risk_levels: np.ndarray) -> pd.DataFrame:"""风险可接受度敏感性分析"""results = []for risk in risk_levels:# 调整风险可接受度modified_rdps = []for rdp in self.base_model.rdps:new_rdp = RDP(id=rdp.id, name=rdp.name,total_demand=rdp.total_demand,rational_demand=rdp.rational_demand,emotional_demand=rdp.emotional_demand,risk_acceptance=risk,weight=rdp.weight,location=rdp.location)modified_rdps.append(new_rdp)modified_asas = []for asa in self.base_model.asas:new_asa = ASA(id=asa.id, name=asa.name, type=asa.type,total_demand=asa.total_demand,rational_demand=asa.rational_demand,emotional_demand=asa.emotional_demand,risk_acceptance=risk,weight=asa.weight,location=asa.location)modified_asas.append(new_asa)modified_model = ReliefSupplyBiLevelModel(self.base_model.rdcs,modified_rdps,modified_asas,self.base_model.transportation)try:result = modified_model.solve_sequential()results.append({'risk_acceptance': risk,'travel_time': result['upper_level']['objective'],'satisfaction': result['lower_level']['objective']})except:continuereturn pd.DataFrame(results)class ReliefSupplyApp:"""Streamlit应用主类"""def __init__(self):self.setup_page_config()self.model = Noneself.results = Nonedef setup_page_config(self):"""页面配置"""st.set_page_config(page_title="救援物资调度双层规划模型",page_icon="🚚",layout="wide",initial_sidebar_state="expanded")def create_default_data(self) -> tuple:"""创建默认测试数据 - 使用英国城市名称"""# 救援物资分配中心 - 使用英国主要城市rdcs = [RDC(1, "伦敦", 30000, 20000, (51.5074, -0.1278)),RDC(2, "曼彻斯特", 35000, 25000, (53.4808, -2.2426)),RDC(3, "伯明翰", 28000, 18000, (52.4862, -1.8904))]# 救援物资需求点 - 增加至8个英国城市rdps = [RDP(1, "利物浦", 15000, 10000, 5000, 0.2, 1.0, (53.4084, -2.9916)),RDP(2, "利兹", 12000, 8000, 4000, 0.2, 0.9, (53.8008, -1.5491)),RDP(3, "格拉斯哥", 18000, 12000, 6000, 0.2, 1.1, (55.8642, -4.2518)),RDP(4, "谢菲尔德", 14000, 9000, 5000, 0.2, 1.0, (53.3811, -1.4701)),RDP(5, "爱丁堡", 16000, 11000, 5000, 0.2, 1.2, (55.9533, -3.1883)),RDP(6, "布里斯托", 13000, 8500, 4500, 0.2, 0.8, (51.4545, -2.5879)),RDP(7, "卡迪夫", 11000, 7000, 4000, 0.2, 0.9, (51.4816, -3.1791)),RDP(8, "贝尔法斯特", 17000, 11500, 5500, 0.2, 1.1, (54.5973, -5.9301))]# 受影响具体区域 - 增加至10个区域asas = [ASA(1, "伦敦东部救援区", "search_rescue", 6000, 4000, 2000, 0.2, 1.2, (51.5400, -0.0557)),ASA(2, "伦敦西部救援区", "search_rescue", 5000, 3500, 1500, 0.2, 1.1, (51.5074, -0.2278)),ASA(3, "曼城北部治疗区", "temporary_treatment", 7000, 5000, 2000, 0.3, 1.3, (53.5008, -2.2426)),ASA(4, "伯明翰居住区A", "temporary_living", 8000, 6000, 2000, 0.25, 1.0, (52.4862, -1.7904)),ASA(5, "利物浦港口区", "temporary_living", 9000, 6500, 2500, 0.25, 1.0, (53.4084, -2.8916)),ASA(6, "格拉斯哥市中心", "search_rescue", 5500, 3800, 1700, 0.2, 1.1, (55.8642, -4.1518)),ASA(7, "爱丁堡老城区", "temporary_treatment", 6500, 4500, 2000, 0.3, 1.2, (55.9533, -3.0883)),ASA(8, "布里斯托工业区", "temporary_living", 7500, 5500, 2000, 0.25, 0.9, (51.4545, -2.4879)),ASA(9, "卡迪夫湾区", "search_rescue", 5800, 4000, 1800, 0.2, 1.0, (51.4816, -3.0791)),ASA(10, "贝尔法斯特港口", "temporary_treatment", 7200, 5200, 2000, 0.3, 1.1, (54.5973, -5.8301))]# 运输时间矩阵 - 更新为英国城市间的近似运输时间(小时)time_rdc_rdp = {# 伦敦到各需求点(0, 0): 3.5, (0, 1): 2.8, (0, 2): 6.5, (0, 3): 2.5, (0, 4): 5.8, (0, 5): 2.2, (0, 6): 2.8, (0, 7): 7.2,# 曼彻斯特到各需求点(1, 0): 0.8, (1, 1): 0.9, (1, 2): 4.2, (1, 3): 1.2, (1, 4): 4.5, (1, 5): 3.2, (1, 6): 3.8, (1, 7): 5.8,# 伯明翰到各需求点(2, 0): 1.8, (2, 1): 1.5, (2, 2): 5.8, (2, 3): 1.2, (2, 4): 5.2, (2, 5): 1.8, (2, 6): 2.2, (2, 7): 6.5}time_rdp_asa = {# 利物浦到各受影响区域(0, 0): 4.2, (0, 1): 4.5, (0, 2): 1.2, (0, 3): 2.1, (0, 4): 0.5, (0, 5): 4.8, (0, 6): 5.2, (0, 7): 3.2, (0, 8): 3.8, (0, 9): 6.2,# 利兹到各受影响区域(1, 0): 3.2, (1, 1): 3.5, (1, 2): 1.5, (1, 3): 1.8, (1, 4): 2.1, (1, 5): 4.2, (1, 6): 4.5, (1, 7): 2.5, (1, 8): 3.1, (1, 9): 5.5,# 格拉斯哥到各受影响区域(2, 0): 7.2, (2, 1): 7.5, (2, 2): 4.8, (2, 3): 6.2, (2, 4): 5.8, (2, 5): 1.2, (2, 6): 1.5, (2, 7): 5.2, (2, 8): 6.8, (2, 9): 2.2,# 谢菲尔德到各受影响区域(3, 0): 2.8, (3, 1): 3.1, (3, 2): 1.2, (3, 3): 1.5, (3, 4): 2.8, (3, 5): 4.5, (3, 6): 4.8, (3, 7): 2.8, (3, 8): 3.4, (3, 9): 5.8,# 爱丁堡到各受影响区域(4, 0): 6.2, (4, 1): 6.5, (4, 2): 4.2, (4, 3): 5.5, (4, 4): 5.2, (4, 5): 1.5, (4, 6): 0.8, (4, 7): 4.8, (4, 8): 6.2, (4, 9): 1.8,# 布里斯托到各受影响区域(5, 0): 2.5, (5, 1): 2.8, (5, 2): 3.5, (5, 3): 1.8, (5, 4): 3.2, (5, 5): 5.2, (5, 6): 5.5, (5, 7): 1.2, (5, 8): 0.8, (5, 9): 4.8,# 卡迪夫到各受影响区域(6, 0): 2.8, (6, 1): 3.1, (6, 2): 3.8, (6, 3): 2.2, (6, 4): 3.5, (6, 5): 5.5, (6, 6): 5.8, (6, 7): 1.5, (6, 8): 1.2, (6, 9): 5.2,# 贝尔法斯特到各受影响区域(7, 0): 7.5, (7, 1): 7.8, (7, 2): 5.8, (7, 3): 6.5, (7, 4): 6.2, (7, 5): 2.5, (7, 6): 2.8, (7, 7): 6.5, (7, 8): 7.2, (7, 9): 1.5}transportation = Transportation("land", time_rdc_rdp, time_rdp_asa)return rdcs, rdps, asas, transportationdef create_sidebar(self) -> Dict:"""创建侧边栏参数输入"""with st.sidebar:st.header("📊 模型参数配置")# 案例选择case_study = st.selectbox("选择案例研究",["英国洪水灾害案例", "自定义参数"])# 不确定性参数st.subheader("不确定性设置")supply_uncertainty = st.slider("供应不确定性系数", 0.0, 1.0, 0.2)demand_uncertainty = st.slider("需求不确定性系数", 0.0, 1.0, 0.3)# 风险可接受度st.subheader("风险可接受度")base_risk = st.slider("基础风险可接受度", 0.0, 0.5, 0.2)# 求解选项st.subheader("求解设置")max_solve_time = st.number_input("最大求解时间(秒)", 60, 3600, 300)return {"case_study": case_study,"supply_uncertainty": supply_uncertainty,"demand_uncertainty": demand_uncertainty,"base_risk": base_risk,"max_solve_time": max_solve_time}def display_model_parameters(self, rdcs, rdps, asas):"""显示模型参数"""st.header("📋 模型参数详情")col1, col2, col3 = st.columns(3)with col1:st.subheader("救援物资分配中心 (RDCs)")rdc_data = []for rdc in rdcs:rdc_data.append({"名称": rdc.name,"容量": f"{rdc.capacity/1000:.1f}千套","库存": f"{rdc.inventory/1000:.1f}千套"})st.dataframe(pd.DataFrame(rdc_data), use_container_width=True)with col2:st.subheader("救援物资需求点 (RDPs)")rdp_data = []for rdp in rdps:rdp_data.append({"名称": rdp.name,"总需求": f"{rdp.total_demand/1000:.1f}千套","风险接受度": f"{rdp.risk_acceptance:.1%}"})st.dataframe(pd.DataFrame(rdp_data), use_container_width=True)with col3:st.subheader("受影响区域 (ASAs)")asa_data = []for asa in asas:asa_data.append({"名称": asa.name,"类型": asa.type,"权重": asa.weight})st.dataframe(pd.DataFrame(asa_data), use_container_width=True)def create_network_visualization(self, results):"""创建物资分配网络图"""if not results:returnst.subheader("🌐 物资分配网络可视化")# 创建网络图数据fig = go.Figure()# 添加节点和边# 这里简化实现,实际应用中需要更复杂的网络布局# 使用桑基图显示物资流动try:source = []target = []value = []label = []# 添加RDC到RDP的流动rdcs = self.model.rdcsrdps = self.model.rdpsasas = self.model.asas# 构建标签for rdc in rdcs:label.append(f"RDC: {rdc.name}")for rdp in rdps:label.append(f"RDP: {rdp.name}")for asa in asas:label.append(f"ASA: {asa.name}")# 构建流动数据x_values = results['upper_level']['x_values']y_values = results['lower_level']['y_values']for (i, j), flow in x_values.items():if flow > 0:source.append(i) # RDC索引target.append(len(rdcs) + j) # RDP索引value.append(flow)for (j, k), flow in y_values.items():if flow > 0:source.append(len(rdcs) + j) # RDP索引target.append(len(rdcs) + len(rdps) + k) # ASA索引value.append(flow)# 创建桑基图fig = go.Figure(go.Sankey(node=dict(pad=15,thickness=20,line=dict(color="black", width=0.5),label=label,color="blue"),link=dict(source=source,target=target,value=value)))fig.update_layout(title_text="救援物资流动网络", font_size=10)st.plotly_chart(fig, use_container_width=True)except Exception as e:st.warning(f"网络可视化生成失败: {e}")def display_results(self, results):"""显示求解结果"""if not results:returnst.header("📈 求解结果")# 关键指标col1, col2, col3, col4 = st.columns(4)with col1:travel_time = results['upper_level']['objective']st.metric("加权行程时间", f"{travel_time:,.0f} 小时",delta="-优化目标")with col2:satisfaction = results['lower_level']['objective']st.metric("感知满意度得分",f"{satisfaction:.4f}",delta="+优化目标")with col3:solve_time = results['solve_time']st.metric("求解时间",f"{solve_time:.2f} 秒",delta="效率指标")with col4:status = results['upper_level']['status']status_color = "🟢" if status == "Optimal" else "🟡"st.metric("求解状态",f"{status_color} {status}")# 物资分配详情st.subheader("📦 详细分配方案")# RDC到RDP分配st.write("**第一阶段: RDC → RDP 分配**")stage1_data = []for (i, j), flow in results['upper_level']['x_values'].items():if flow > 0:stage1_data.append({"来源": self.model.rdcs[i].name,"目标": self.model.rdps[j].name,"分配量(套)": f"{flow:,.0f}","比例": f"{(flow/self.model.rdcs[i].inventory*100):.1f}%"})st.dataframe(pd.DataFrame(stage1_data), use_container_width=True)# RDP到ASA分配st.write("**第二阶段: RDP → ASA 分配**")stage2_data = []for (j, k), flow in results['lower_level']['y_values'].items():if flow > 0:stage2_data.append({"来源": self.model.rdps[j].name,"目标": self.model.asas[k].name,"分配量(套)": f"{flow:,.0f}","类型": self.model.asas[k].type})st.dataframe(pd.DataFrame(stage2_data), use_container_width=True)# 网络可视化self.create_network_visualization(results)def run_sensitivity_analysis(self):"""运行敏感性分析"""st.header("🔬 敏感性分析")if self.model is None:st.warning("请先求解基础模型")returnanalysis = UncertaintyAnalysis(self.model)# 风险可接受度敏感性分析st.subheader("风险可接受度敏感性分析")risk_levels = np.linspace(0.05, 0.4, 10)with st.spinner("正在进行敏感性分析..."):risk_results = analysis.sensitivity_analysis_risk(risk_levels)if not risk_results.empty:# 创建双Y轴图表fig = go.Figure()# 添加行程时间线fig.add_trace(go.Scatter(x=risk_results['risk_acceptance'],y=risk_results['travel_time'],name="加权行程时间",line=dict(color='red', width=2)))# 添加满意度线(次Y轴)fig.add_trace(go.Scatter(x=risk_results['risk_acceptance'],y=risk_results['satisfaction'],name="感知满意度",line=dict(color='blue', width=2),yaxis="y2"))fig.update_layout(title="风险可接受度敏感性分析",xaxis_title="风险可接受度",yaxis=dict(title="加权行程时间(小时)", side="left", color="red"),yaxis2=dict(title="感知满意度", side="right", overlaying="y", color="blue"),legend=dict(x=0, y=1))st.plotly_chart(fig, use_container_width=True)# 显示分析结论st.info("""**分析结论:**- 风险可接受度与行程时间呈正相关关系- 较低的risk值可能导致满意度下降但行程时间优化- 决策者需要在效率与公平性之间权衡""")def run_monte_carlo_simulation(self):"""运行蒙特卡洛仿真"""st.header("🎲 蒙特卡洛仿真分析")if self.model is None:st.warning("请先求解基础模型")returnn_simulations = st.slider("仿真次数", 10, 100, 50)analysis = UncertaintyAnalysis(self.model)with st.spinner("正在进行蒙特卡洛仿真..."):mc_results = analysis.monte_carlo_supply_analysis(n_simulations)if not mc_results.empty:# 显示统计结果col1, col2 = st.columns(2)with col1:st.metric("平均行程时间", f"{mc_results['travel_time'].mean():.0f}小时")st.metric("行程时间变异系数", f"{(mc_results['travel_time'].std()/mc_results['travel_time'].mean()*100):.1f}%")with col2:st.metric("平均满意度", f"{mc_results['satisfaction'].mean():.4f}")st.metric("成功率", f"{(len(mc_results)/n_simulations*100):.1f}%")# 创建分布图fig = px.histogram(mc_results, x='travel_time', title='行程时间分布', labels={'travel_time': '加权行程时间(小时)'})st.plotly_chart(fig, use_container_width=True)def run(self):"""主运行函数"""st.title("🚚 救援物资跨区域调度双层规划模型")st.markdown("基于幸存者感知满意度和风险可接受度的优化决策支持系统")# 获取参数配置params = self.create_sidebar()# 创建模型数据rdcs, rdps, asas, transportation = self.create_default_data()# 显示模型参数self.display_model_parameters(rdcs, rdps, asas)# 创建模型实例self.model = ReliefSupplyBiLevelModel(rdcs, rdps, asas, transportation)# 求解控制st.header("🎮 模型求解控制")col1, col2, col3 = st.columns([1, 1, 2])with col1:if st.button("🚀 求解双层规划模型", type="primary", use_container_width=True):with st.spinner("正在求解双层规划模型..."):self.results = self.model.solve_sequential()st.success("求解完成!")with col2:if st.button("🔬 敏感性分析", use_container_width=True):self.run_sensitivity_analysis()with col3:if st.button("🎲 蒙特卡洛仿真", use_container_width=True):self.run_monte_carlo_simulation()# 显示结果if self.results:self.display_results(self.results)# 模型说明with st.expander("📖 模型说明"):st.markdown("""### 模型特性- **双层规划结构**: 上层优化效率(行程时间),下层优化公平性(感知满意度)- **风险可接受度**: 确保基本救援需求得到满足- **不确定性处理**: 支持供应、需求、时间不确定性分析### 关键技术- 使用PuLP进行线性规划求解- 顺序求解策略处理双层优化- 基于Plotly的交互式可视化- 蒙特卡洛仿真分析不确定性影响### 案例设置- **英国洪水灾害场景**: 使用英国主要城市作为救援节点- **扩展规模**: 3个分配中心,8个需求点,10个受影响区域- **地理分布**: 覆盖英格兰、苏格兰、威尔士和北爱尔兰""")def main():"""主函数"""app = ReliefSupplyApp()app.run()if __name__ == "__main__":main()