PPO算法：从深度学习视角入门强化学习

1. 强化学习：不只是“监督学习”

• 在深度学习中，我们习惯于监督学习的范式：给模型一堆 (输入, 正确标签) 对，模型通过最小化预测与标签之间的差距来学习。比如，给一张猫的图片，标签是“猫”。但强化学习完全不同。想象一下你在教一只小狗“坐下”：
  • 你不会直接告诉它“你的神经元权重应该这样调整”。
  • 你只会给它一个指令（比如“坐下”），然后观察它的动作。
  • 如果它做对了，你就给它一个零食（奖励）；如果做错了，你可能什么也不给，或者说“不”（负奖励）。
  • 经过多次尝试，小狗会自己学会哪些动作（在什么状态下）能获得最多的零食。

这就是强化学习的核心思想。我们来定义几个基本术语：

• 智能体：就是你的小狗，或者我们代码里的模型。它负责做决策。
• 环境：小狗所处的世界，包括你和它自己。环境会根据智能体的动作，给出新的状态和奖励。
• 状态：对当前环境的描述。比如，“你站着，小狗也站着”。
• 动作：智能体可以执行的操作。比如，“小狗坐下”。
• 奖励：环境对智能体动作的即时反馈。比如，“+1（一个零食）”或“0（没有零食）”。

RL的目标：训练一个智能体，让它学会一个策略，这个策略能在任何状态下，选择能最大化长期累积奖励的动作。

与深度学习的连接：在深度学习中，我们用神经网络来拟合一个从输入到标签的函数 f(x) -> y。在强化学习中，我们同样用神经网络，但目标是拟合一个策略函数 π(a|s)，它输入一个状态 s，输出一个概率分布，表示在当前状态下执行每个动作 a 的概率。

2. PPO的“学前班”：必备基础概念

在深入PPO之前，我们需要先理解几个它赖以构建的基石。

2.1 马尔可夫决策过程

• 这个名字听起来吓人，但思想很简单：“未来只取决于现在，与过去无关”。
  就像下棋，你下一步该怎么走，只取决于当前棋盘的局面（当前状态），而与你之前是怎么走到这个局面的（历史动作序列）无关。MDP就是对这个“无记忆”过程的数学描述。它确保了我们只需要关注当前状态 S_t 来做决策，大大简化了问题。

2.2 折扣因子

• 我们希望最大化“长期累积奖励”，但这个“长期”是多久？而且，未来的奖励不如眼前的奖励“值钱”。今天的100块比明天的100块更有吸引力。

• 折扣因子 γ (gamma) 就是用来衡量这个概念的。它是一个介于0和1之间的数。我们计算的不是所有未来奖励的简单相加，而是折扣累积奖励：
  $G_t=R_t+\gamma \ast R_{t+1}+{\gamma }^2\ast R_{t+2}+...$

  • 如果 γ 接近0，智能体会非常“短视”，只关心眼前的奖励。
  • 如果 γ 接近1，智能体会非常有“远见”，愿意为了长远的巨大回报而牺牲眼前的利益。

2.3 价值函数

如何评估一个状态或一个动作的“好坏”？价值函数就是答案。

• 状态价值函数 V(s)：从状态 s 出发，遵循某个策略，未来能获得的期望折扣累积奖励。它回答了：“当前这个局面有多好？”
• 动作价值函数 Q(s, a)：在状态 s 下，执行动作 a，然后遵循某个策略，未来能获得的期望折扣累积奖励。它回答了：“在当前局面下，这么做有多好？”

与深度学习的连接：V(s) 和 Q(s, a) 都可以用神经网络来拟合。想象一下，你训练一个网络，输入一张游戏截图（状态s），输出一个分数（V(s)），这个分数预测了你最终能得多少分。这就是价值网络。

2.4 策略梯度

• 这是连接深度学习和强化学习的关键桥梁。我们有一个策略网络 π_θ（θ是网络参数），我们想调整 θ 来让智能体表现更好。但问题来了：我们没有“正确动作”的标签，怎么计算梯度呢？

• 策略梯度的思想非常巧妙：如果一个动作带来了比预期更好的结果，我们就应该增加它在未来被选择的概率；反之，则降低其概率。 其核心梯度公式可以简化理解为：${\nabla }_{\theta }J(\theta )\approx E[(Q(s,a)-V(s))\ast {\nabla }_{\theta }log{\pi }_{\theta }(a|s)]$

  • Q(s, a) - V(s) 被称为优势函数 A(s, a)。它表示动作 a 比在状态 s 下的“平均表现”好多少或差多少。
  • 如果 A(s, a) > 0（动作比平均好），梯度方向就和 ∇_θ log π_θ(a|s) 一致，增加这个动作的概率。
  • 如果 A(s, a) < 0（动作比平均差），梯度方向就和 ∇_θ log π_θ(a|s) 相反，降低这个动作的概率。

• 这样，我们就有了更新策略网络的“方向”！

3. PPO的核心：稳定与高效的“艺术”

• 传统的策略梯度方法有一个大问题：数据利用率低。每次更新策略后，旧策略产生的数据就不能再用了，必须用新策略重新收集数据。这太浪费了！
• PPO就是为了解决这个问题而生的，它的全称是Proximal Policy Optimization（近端策略优化），核心思想是：用旧策略的数据来更新新策略，但要小心，别让新策略“走得太远”。

3.1 Actor-Critic 架构

PPO通常采用Actor-Critic架构，这就像一个剧组：

• Actor（演员）：就是我们的策略网络 ${\pi }_{\theta }$。它负责在给定状态下“表演”，即选择一个动作。
• Critic（评论家）：就是我们的价值网络 $V_{\phi }$。它负责观看Actor的表演，并给出评价，即计算状态价值 $V(s)$ 或优势 A(s, a)。

Actor根据Critic的评价来调整自己的“演技”（更新策略参数），而Critic也在不断学习如何更准确地评价（更新价值参数）。两者相互促进，共同进步。

3.2 重要性采样

• n这是PPO能够“复用数据”的魔法。我们想用旧策略 ${\pi }_{{\theta }_{old}}$ 收集的数据 $(s,a,r)$ 来更新新策略 ${\pi }_{\theta }$。
• 直接用旧数据计算新策略的梯度会有偏差，因为数据分布不同。重要性采样提供了一个修正系数：$$\text{重要性权重}=\frac{{\pi }_{\theta }(a|s)}{{\pi }_{{\theta }_{\text{old}}}(a|s)}$$
  这个权重衡量了新旧策略在同一个状态 s 下，选择同一个动作 a 的概率变化。通过这个权重，我们就可以“校正”旧数据，使其适用于新策略的更新。

3.3 裁剪功能：PPO的“安全带”

• 重要性采样虽然强大，但有一个致命风险：如果新旧策略差异太大，这个权重会变得极不稳定，可能导致训练崩溃。
• PPO的精髓就在于裁剪。它给重要性权重加了一个“限制器”，确保新策略不会偏离旧策略太远。
• PPO的目标函数（简化版）如下：
  $$L^{\text{CLIP}}(\theta )={\mathbb{E}}_t\left[\min \left(r_t(\theta )A_t,\text{clip}\left(r_t(\theta ),1-ϵ,1+ϵ\right)A_t\right)\right]$$
  • r_t(θ) 就是重要性权重 π_θ(a|s) / π_θ_old(a|s)，ε 是一个很小的超参数（如0.2），A_t 是优势函数。

这个公式看起来复杂，但思想很直观：

1. 当优势 $A_t>0$（好动作）：
   • 我们希望增加这个动作的概率，即希望 r_t(θ) 变大。
   • 但 min 函数限制了它。如果 r_t(θ) 超过了 1+ε，clip 函数会把它“裁剪”到 1+ε。此时，min 会选择被裁剪后的值，这意味着目标函数不会再增加了，梯度也消失了。
   • 效果：对于好动作，我们允许其概率增加，但最多只能增加到旧策略的 1+ε 倍，防止步子迈得太大。
2. 当优势 $A_t<0$（坏动作）：
   • 我们希望降低这个动作的概率，即希望 r_t(θ) 变小。
   • min 函数同样会限制它。如果 r_t(θ) 小于 1-ε，clip 会把它裁剪到 1-ε。此时，min 会选择未被裁剪的、更小的 r_t(θ) * A_t（因为A_t是负数，乘以更小的r_t会得到更大的值，即更小的损失）。
   • 效果：对于坏动作，我们允许其概率降低，但最多只能降低到旧策略的 1-ε 倍。

这个小小的 min 和 clip 组合，就像一个安全带，让策略更新既有效又稳定，是PPO算法成功的核心。

3.4 KL散度

• KL散度是衡量两个概率分布“差异”的指标。在PPO的一些变体中，它被用作另一种“安全带”。比如，可以设定一个目标，让新旧策略的KL散度不能超过某个阈值。如果超过了，就停止更新或施加惩罚。裁剪目标函数实际上是一种隐式地约束KL散度的方法。

4. PPO核心公式一览

现在，我们把所有部分拼起来。PPO的最终损失函数通常是三部分的加权和：
$$L(\theta )=E[L_{CLIP}(\theta )-c1\ast L_{VF}(\theta )+c2\ast S[{\pi }_{\theta }](s)]$$

• $L_{CLIP}(\theta )$：就是我们上面详细讲的裁剪策略目标，用于更新Actor。
• $L_{VF}(\theta )$：价值函数损失。通常是均方误差 MSE(V_φ(s), G_t)，用于更新Critic，让它对价值的估计更准。G_t是实际的折扣累积回报。
• $S[{\pi }_{\theta }](s)$：熵奖励。熵衡量了策略的“随机性”。鼓励熵可以防止策略过早地收敛到一个确定性策略（比如在某个状态下永远只选一个动作），从而保持探索能力。这在训练初期尤其重要。

c1 和 c2 是平衡这三项的超参数。

5. PPO代码实现思路

• 纸上得来终觉浅，绝知此事要躬行。在理解了PPO的理论之后，让我们通过一个经典的案例——CartPole（倒立摆）——来亲手实现PPO算法。这个案例将把前面所有的抽象概念都具体化。

5.1 案例目标

我们的目标是训练一个智能体，让它学会控制一个小车上的杆子，使其保持竖直平衡。

• 环境：CartPole-v1，一个由OpenAI Gymnasium提供的标准测试环境。
• 状态：智能体能观察到4个维度的信息：
  1. 小车的位置
  2. 小车的速度
  3. 杆子的角度
  4. 杆子的角速度
• 动作：智能体可以执行2个离散动作：
  1. 向左施力
  2. 向右施力
• 奖励：每成功保持杆子平衡一步，智能体获得+1的奖励。如果杆子倒下或小车移出边界，则回合结束。
• 成功标准：杆子在连续500步内不倒下，即认为任务解决。

5.2 案例内容

我们将使用PyTorch构建两个核心神经网络：

1. Actor（策略网络）：输入当前状态（4个维度），输出执行每个动作的概率（2个概率值之和为1）。它负责做决策。
2. Critic（价值网络）：输入当前状态（4个维度），输出一个标量，表示对该状态未来能获得总奖励的估计。它负责评估Actor决策的好坏。

训练过程将遵循我们之前讨论的PPO流程：与环境交互收集数据 -> 计算优势函数 -> 使用裁剪的目标函数更新Actor和Critic网络。

5.3 代码实现思路

代码分为以下几个部分：

1. 网络定义：创建Actor和Critic两个PyTorch模型类。
2. PPO算法类：创建一个PPO类，封装所有核心逻辑，包括：
   • 初始化网络和优化器。
   • update方法：接收一个回合的数据，执行PPO的核心更新逻辑（计算裁剪损失、价值损失、熵奖励，并更新网络）。
   • train方法：主训练循环，负责与环境交互、收集数据，并定期调用update方法。
3. 主程序：实例化环境和PPO智能体，并启动训练。

下面是带有详细注释的完整代码实现。

# 导入所需的库
import gymnasium as gym
import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
from IPython.display import clear_output
# 注意：某些版本的gymnasium可能与新版numpy不兼容，如遇问题可尝试固定numpy版本
# pip uninstall numpy
# pip install numpy==1.24.3
# --- 1. 网络定义 ---
# 策略网络：用于决定在给定状态下采取什么动作
class Actor(nn.Module):def __init__(self, state_dim, action_dim):super(Actor, self).__init__()# 构建一个简单的三层全连接神经网络self.network = nn.Sequential(nn.Linear(state_dim, 64),  # 输入层 -> 隐藏层1nn.Tanh(),                 # 激活函数，增加非线性nn.Linear(64, 64),         # 隐藏层1 -> 隐藏层2nn.Tanh(),                 # 激活函数nn.Linear(64, action_dim), # 隐藏层2 -> 输出层nn.Softmax(dim=-1)         # 将输出转换为概率分布，确保所有动作概率和为1)def forward(self, state):return self.network(state)  # 前向传播，输出动作概率分布# 价值网络：用于评估状态的价值
class Critic(nn.Module):def __init__(self, state_dim):super(Critic, self).__init__()# 构建一个简单的三层全连接神经网络self.network = nn.Sequential(nn.Linear(state_dim, 64),  # 输入层 -> 隐藏层1nn.Tanh(),                 # 激活函数nn.Linear(64, 64),         # 隐藏层1 -> 隐藏层2nn.Tanh(),                 # 激活函数nn.Linear(64, 1)           # 隐藏层2 -> 输出层（输出一个标量，即状态价值V(s)）)def forward(self, state):return self.network(state)  # 前向传播，输出状态价值# --- 2. PPO算法实现 ---
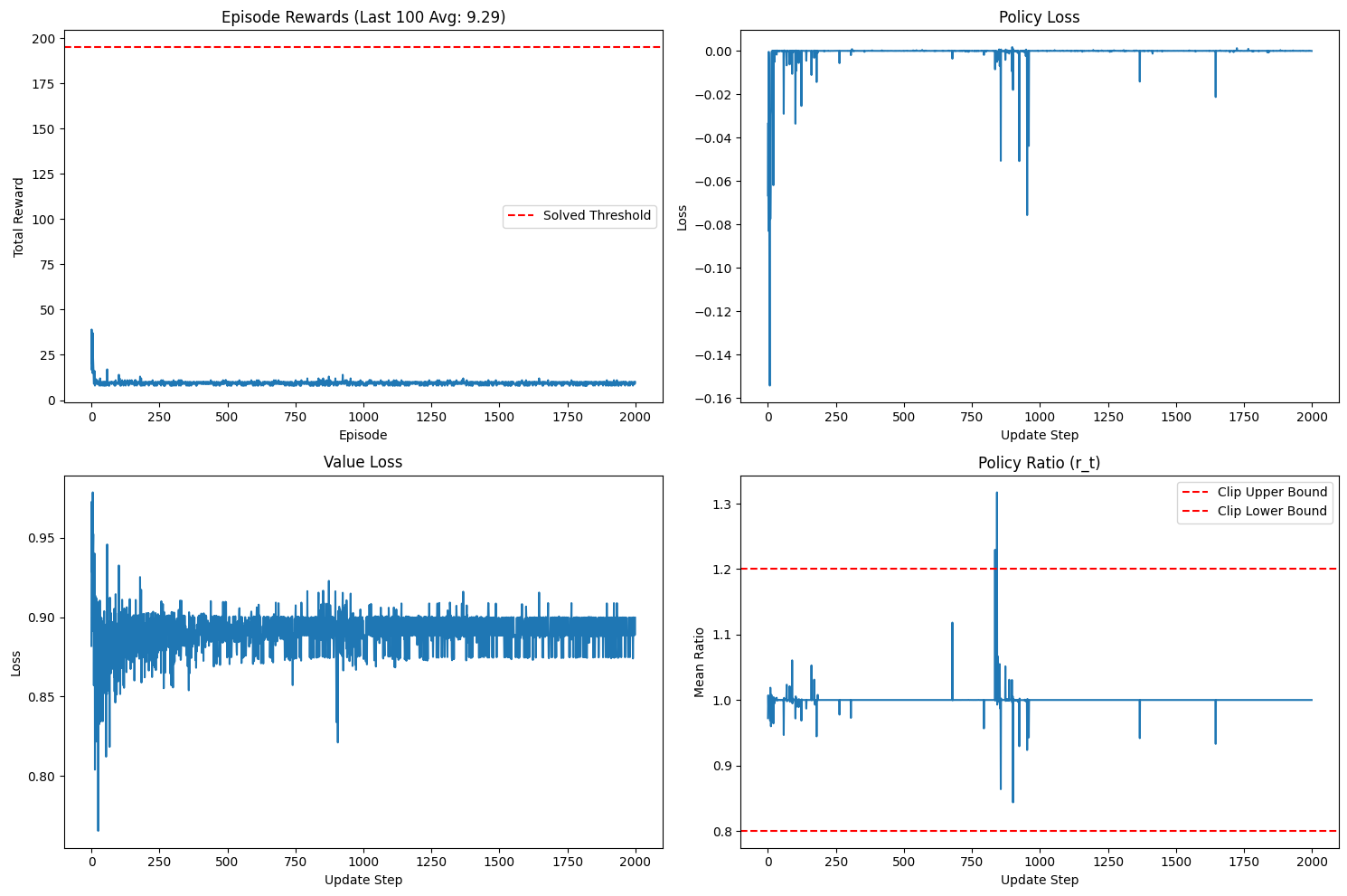
class PPO:def __init__(self, state_dim, action_dim, lr=0.0003, gamma=0.99, epsilon=0.2, c1=0.5, c2=0.01):"""初始化PPO智能体Args:state_dim (int): 状态空间的维度 (CartPole中为4)action_dim (int): 动作空间的维度 (CartPole中为2)lr (float): 学习率gamma (float): 折扣因子，用于计算未来奖励epsilon (float): PPO裁剪范围，限制策略更新的幅度c1 (float): 价值函数损失的权重系数c2 (float): 熵奖励的权重系数"""# 初始化策略网络和价值网络self.actor = Actor(state_dim, action_dim)self.critic = Critic(state_dim)# 为Actor和Critic分别创建Adam优化器self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=lr)self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=lr)# 设置PPO算法的超参数self.gamma = gamma      # 折扣因子self.epsilon = epsilon  # 裁剪参数self.c1 = c1            # 价值损失系数self.c2 = c2            # 熵奖励系数# 用于存储一个回合中收集到的数据self.memory = {'states': [], # 存储所有经历的状态'actions': [], # 存储所有执行的动作'old_log_probs': [], # 存储动作的原始概率'rewards': [], # 存储获得的奖励'dones': [] # 存储是否结束的标志}# 记录训练过程中的指标，用于可视化self.rewards_history = [] # 记录每个episode的总奖励self.policy_losses = [] # 记录策略网络的损失self.value_losses = [] # 记录价值网络的损失self.ratios = [] # 记录策略更新的比率def store_transition(self, state, action, reward, done, old_log_prob):"""将一步的交互数据存入内存"""self.memory['states'].append(state)self.memory['actions'].append(action)self.memory['old_log_probs'].append(old_log_prob)self.memory['rewards'].append(reward)self.memory['dones'].append(done)def compute_advantages(self, rewards, dones, values, next_values):"""计算GAE (Generalized Advantage Estimation) 或 简单的优势函数这里使用简化的TD-Error作为优势函数A(s,a) = R + γ * V(s') - V(s)"""advantages = rewards + self.gamma * next_values * (1 - dones) - values# 标准化优势函数，有助于训练稳定return (advantages - advantages.mean()) / (advantages.std() + 1e-8)def update(self):"""使用收集到的数据更新策略网络和价值网络"""# 将内存中的列表转换为PyTorch张量states = torch.stack(self.memory['states'])actions = torch.stack(self.memory['actions'])old_log_probs = torch.stack(self.memory['old_log_probs'])rewards = torch.FloatTensor(self.memory['rewards'])dones = torch.FloatTensor(self.memory['dones'])# --- 计算优势函数 ---with torch.no_grad(): # 在此块中不计算梯度values = self.critic(states).squeeze()# 使用价值网络(critic)评估每个状态的价值# 例如：states中有100个状态，每个状态得到一个价值估计# 获取下一个状态的价值# values[1:] 取除了第一个状态之外的所有状态的价值# torch.tensor([[0.0]]) 在最后补一个0（因为最后一个状态没有下一个状态）next_values = torch.cat([values[1:], torch.tensor([0.0])])# 计算优势函数：Q(s,a) - V(s)advantages = self.compute_advantages(rewards, dones, values, next_values)returns = advantages + values # 计算回报 G_t = A_t + V(s)# 清空内存，为下一个回合的数据收集做准备for key in self.memory:self.memory[key].clear()# --- PPO核心更新循环 ---# 对同一批数据进行多次更新，提高数据利用率for _ in range(10): # 重新计算当前策略下的动作概率current_probs = self.actor(states)dist = torch.distributions.Categorical(current_probs)current_log_probs = dist.log_prob(actions)# 1. 计算重要性采样比率 r_t(θ)ratios = torch.exp(current_log_probs - old_log_probs)# 2. 计算裁剪的策略目标 L_CLIPsurr1 = ratios * advantagessurr2 = torch.clamp(ratios, 1 - self.epsilon, 1 + self.epsilon) * advantagespolicy_loss = -torch.min(surr1, surr2).mean()# 3. 计算价值函数损失 L_VFvalue_pred = self.critic(states).squeeze()value_loss = nn.functional.mse_loss(value_pred, returns)# 4. 计算熵奖励 S[π_θ](s)entropy = dist.entropy().mean()# 5. 计算总损失# L(θ) = L_CLIP - c1 * L_VF + c2 * S# 注意：我们是最小化损失，所以价值损失是加，熵奖励是减（因为我们要最大化熵）total_loss = policy_loss + self.c1 * value_loss - self.c2 * entropy# --- 更新网络 ---# 更新Actorself.actor_optimizer.zero_grad()policy_loss.backward(retain_graph=True) # 保留计算图，因为Critic还要用self.actor_optimizer.step()# 更新Criticself.critic_optimizer.zero_grad()value_loss.backward()self.critic_optimizer.step()# 记录本轮更新的指标self.ratios.append(ratios.mean().item())self.policy_losses.append(policy_loss.item())self.value_losses.append(value_loss.item())def plot_training_data(self, episode):"""可视化训练过程中的各项指标"""clear_output(wait=True)fig, axs = plt.subplots(2, 2, figsize=(15, 10))# 绘制每个回合的总奖励axs[0, 0].plot(self.rewards_history)axs[0, 0].set_title(f'Episode Rewards (Last 100 Avg: {np.mean(self.rewards_history[-100:]):.2f})')axs[0, 0].set_xlabel('Episode')axs[0, 0].set_ylabel('Total Reward')axs[0, 0].axhline(y=195, color='r', linestyle='--', label='Solved Threshold')axs[0, 0].legend()# 绘制策略损失axs[0, 1].plot(self.policy_losses)axs[0, 1].set_title('Policy Loss')axs[0, 1].set_xlabel('Update Step')axs[0, 1].set_ylabel('Loss')# 绘制价值损失axs[1, 0].plot(self.value_losses)axs[1, 0].set_title('Value Loss')axs[1, 0].set_xlabel('Update Step')axs[1, 0].set_ylabel('Loss')# 绘制策略比率axs[1, 1].plot(self.ratios)axs[1, 1].set_title('Policy Ratio (r_t)')axs[1, 1].set_xlabel('Update Step')axs[1, 1].set_ylabel('Mean Ratio')axs[1, 1].axhline(y=1+self.epsilon, color='r', linestyle='--', label='Clip Upper Bound')axs[1, 1].axhline(y=1-self.epsilon, color='r', linestyle='--', label='Clip Lower Bound')axs[1, 1].legend()plt.tight_layout()plt.show()def train(self, env, episodes=1000):"""主训练循环"""for episode in range(episodes):state, _ = env.reset()done = Falseepisode_reward = 0while not done:# 将状态转换为张量state_tensor = torch.FloatTensor(state)# Actor选择动作with torch.no_grad():probs = self.actor(state_tensor)dist = torch.distributions.Categorical(probs)action = dist.sample()log_prob = dist.log_prob(action)# 与环境交互next_state, reward, terminated, truncated, _ = env.step(action.item())done = terminated or truncated# 存储这一步的轨迹self.store_transition(state_tensor, action, reward, done, log_prob)state = next_stateepisode_reward += reward# 一个回合结束，使用收集到的数据更新网络self.update()self.rewards_history.append(episode_reward)# 定期打印和绘图if (episode + 1) % 100 == 0:avg_reward = np.mean(self.rewards_history[-100:])print(f"Episode {episode + 1}, Average Reward (last 100): {avg_reward:.2f}")self.plot_training_data(episode)# 检查是否已解决if avg_reward >= 195.0:print(f"Environment solved in {episode + 1} episodes!")break
# --- 3. 主程序 ---
if __name__ == "__main__":# 创建CartPole环境，render_mode="human"可以可视化，但会拖慢训练速度# 训练时可以设为 None 或 "rgb_array"env = gym.make('CartPole-v1', render_mode=None) # 获取状态和动作空间的维度state_dim = env.observation_space.shape[0]action_dim = env.action_space.n# 创建PPO智能体实例ppo_agent = PPO(state_dim, action_dim)# 开始训练ppo_agent.train(env, episodes=2000)# 关闭环境env.close()