《数据结构风云》递归算法：二叉树遍历的精髓实现

🔥@晨非辰Tong： 个人主页
👀专栏：《C语言》、《数据结构与算法入门指南》
💪学习阶段：C语言、数据结构与算法初学者
⏳“人理解迭代，神理解递归。”

---

---

引言

  代码修行路上，你是否曾为盘根错节的二叉树所困？今日，我便传你一门无上法门——递归分神之术。
  此法看似玄奥，实则暗合天道。面对复杂树结构，只需一剑化三清：本尊镇守当前，分神各巡左右。如此层层分化，直至洞悉所有脉络。
  修得此术，任他树中有树、套中有套，你自能一眼洞穿虚实。三式法诀，助你练就火眼金睛，识破万千子树真伪。

》–获取源码–点我《

---

一、单值二叉树

–965. 单值二叉树

1.目标特征描述：什么单值二叉树

2.目标实现示例：

3.算法思路：

先对简单二叉树进行算法推理，再推广到整体。

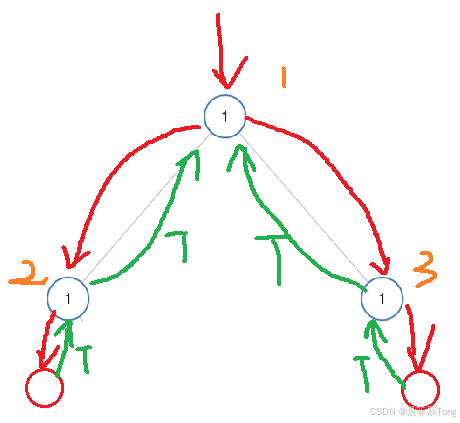
  递归规则：先递进再返回。
  递进：首先从根节点root开始，左子树如果存在先对左子树匹配判断：若二者数值不相等，就返回false，反之继续对右子树进行判断：二者数值不相等，返回false。当然，根节点为空返回true。推广到整体，就遍历左右子树判断。
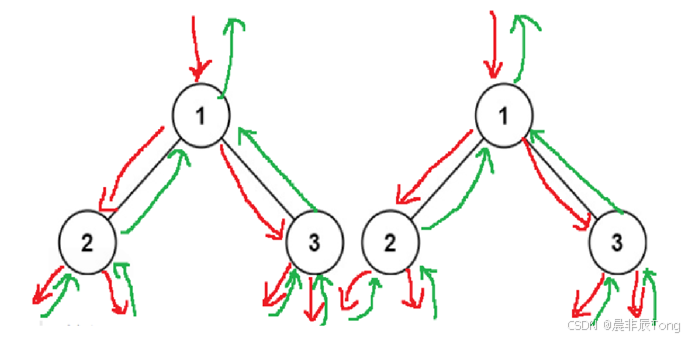
  返回：整个二叉树已经递进判断完毕，要对函数从最后开始返回：看图示，第2节点的左右子节点（&&的和关系）为空，那么都返回true，代表这个子树是单值的。右子树第3节点也是单值的。那么根节点的两个子树就都返回true（&&的和关系），代表整体是单值二叉树。

3.1 具体代码实现

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*/
bool isUnivalTree(struct TreeNode* root) 
{//首先判断树是否为空if(root == NULL){return true;}//存在左子树再匹配if(root->left && root->val != root->left->val){return false;}if(root->right && root->val != root->right->val){return false;}return isUnivalTree(root->left) && isUnivalTree(root->right);
}

• 时间复杂度: O(N)；
• 空间复杂度: O(N)；

---

二、相同的树

–100. 相同的树

1.目标特征描述：什么是相同的树

2.目标实现示例

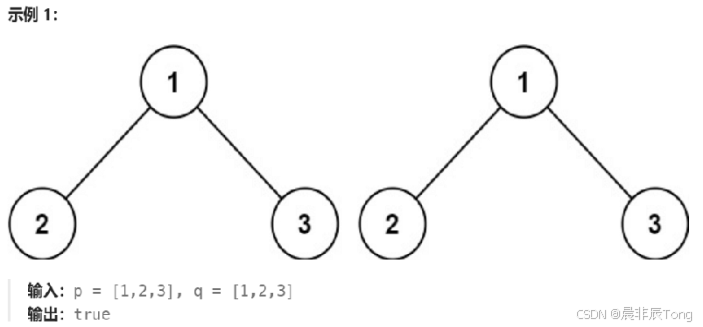
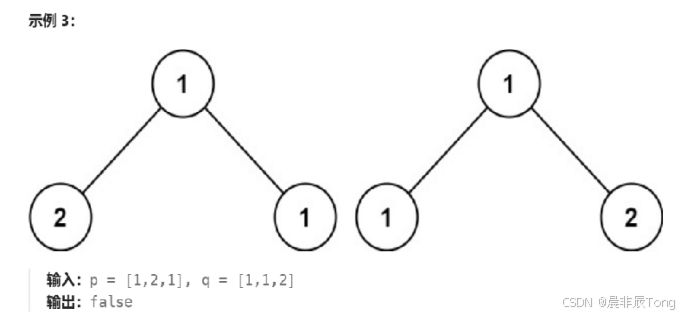
3.算法思路

情况分类	两根节点情况	结果
1	两个根节点都为空	是相同的树
2	一个根节点为空，另一个不为空	不是相同的树
3	两个根节点都不为空	比较节点数值进一步判断

  --根据函数递归规则：
  递进：从两个树根节点进行对比，第1种情况两个根节点都为空（代表没有子节点）就返回true；第2种情况一个根节点为空，另一个根节点不为空，两个树的结构不同，就返回false；第3种情况两个根节点都不为空，那么就要判断两个节点的数值，不相等就返回false。最后开始调用函数对比二者的左右子树。
  返回：从函数的最后开始返回。看图示，从二者的第2个节点的左右子树开始对比，左右节点都为空返回true（&&的和关系），代表两个二叉树的第2节点为根节点子树为相同的树。同理，二者的以第3个节点为根节点的子树也是相同的树。以此类推，根节点的左右子树都是相同的树（&&的关系），代表两个二叉树为相同的二叉树。

3.1 具体代码实现

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*/
bool isSameTree(struct TreeNode* p, struct TreeNode* q) 
{//两个根节点都为空-->结构相同if(p == NULL && q == NULL){return true;} //只有一个根节点为空-->结构不同if(p == NULL || q == NULL){return false;}   //两个根节点都不为空，但值不相等if(p->val != q->val){return false;}//否则继续遍历判断子树return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

---

三、另一棵树的子树

–572. 另一棵树的子树

1.目标特征描述

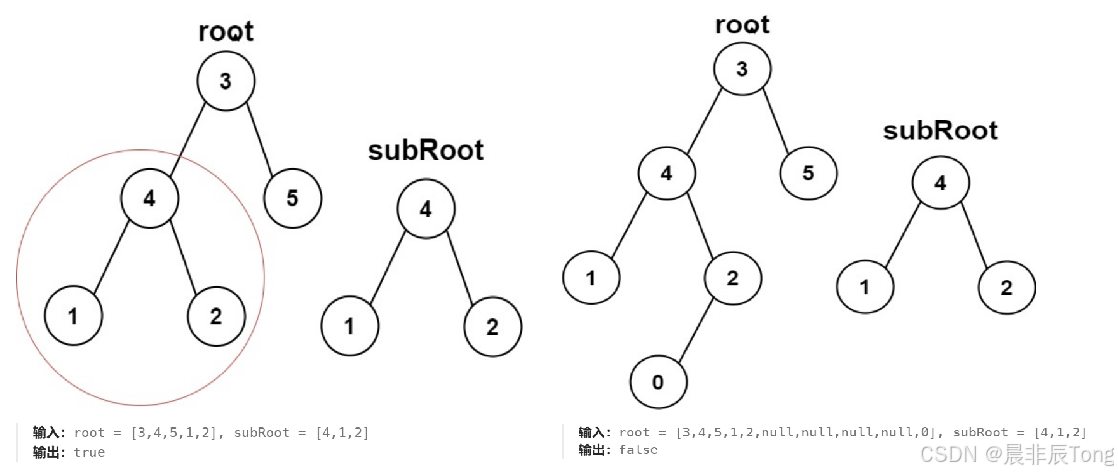
2.目标实现示例

3.算法思路

  基本算法：首先，如果根节点为空，就不需要与目标树再进行对比。不为空，就利用前面实现的判断是否是相同的树接口进行判断。不匹配，就调用函数遍历子树（注意：当左子树匹配成功，就不需要再对右子树进行判断 ）。

3.1 具体代码实现

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*/typedef struct TreeNode TreeNode;
bool isSametree(TreeNode* p, TreeNode* q)
{//第1种情况，两个书都为空if(p == NULL && q == NULL){return true;}//第2种情况，其中1个根节点为空if(p == NULL || q == NULL){return false;}//第3种情况，2个根节点存在，但是数值不相同if(p->val != q->val){return false;}//数值相同，向下进行调用函数判断子树return isSametree(p->left, q->left) && isSametree(p->right, q->right);
}bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) 
{if(root == NULL){return false;}//调用判断最开始时根节点是否匹配if(isSametree(root, subRoot)){return true;}    //根节点不匹配，向下递归调用return isSubtree(root->left, subRoot) || isSubtree(root->right,subRoot);
}

---

四、对称二叉树

–101. 对称二叉树

1.目标特征描述

2.目标实现示例

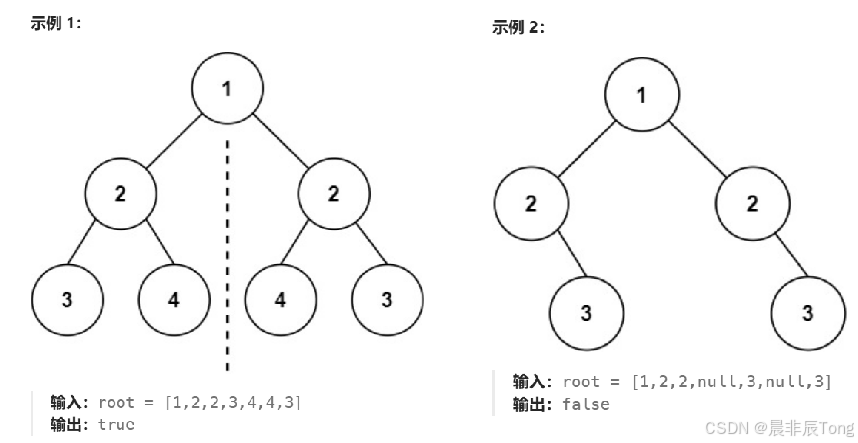
3.算法思路

  首先根节点为空，代表树为空，一定是对称的。不为空，将根节点的左右子树判断结构是否对称——>改变一下前面实现相同的树的接口：return isSametree(p->left, q->right) && isSametree(p->right, q->left);，因为让左右对应进行对比。
  如果函数判断后，返回的false，那么就直接返回false。

3.1 具体代码实现

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*/typedef struct TreeNode TreeNode;
bool isSametree(TreeNode* p, TreeNode*q)
{//根节点都为空if(p == NULL && q == NULL){return true;}//一个根节点为空if(p == NULL || q == NULL){return false;}//不为空，但是数值不同if(p->val != q->val){return false;}//以上均不满足，代表这两个节点相同，遍历子树继续判断return isSametree(p->left, q->right) && isSametree(p->right, q->left);
}bool isSymmetric(struct TreeNode* root)
{//树为空if(root == NULL){return true;}//树不为空,将左右子树进行对比，看结构是否对称if(isSametree(root->left, root->right)){return true;}return false;
}

总结

道阻且长，行则将至
  四大递归心法已传授完毕，但这只是算法修真的起点。递归分神的精髓，将在后续的图论、动态规划等秘境中继续发挥威力。
  保持这份求道之心，我们下期「回溯秘境」再会！
  愿每一位码农修行者，都能在算法之道上突破自我。