全连接层的第二层是怎么减少神经节点数
在卷积神经网络中,拉平(Flatten)后的全连接层(FC 层)之所以能减少神经节点数(即维度压缩),核心是通过权重矩阵的维度设计和特征的加权组合实现的,本质是对高维特征进行 “筛选与压缩”,保留关键信息的同时降低维度。以下结合具体案例详细说明:
一、前提:拉平后的特征向量是高维的
卷积层输出的特征图通常是多维的(如7×7×256,表示 7×7 的空间尺寸,256 个通道),拉平(Flatten)后会转换为一维向量,维度为 7×7×256 = 12544(即 12544 个特征值)。这个高维向量会作为第一层全连接层的输入。
二、全连接层减少节点数的核心:权重矩阵的 “降维映射”
全连接层的相邻两层之间通过权重矩阵连接,下一层的节点数由权重矩阵的维度直接决定。假设拉平后的向量为X(维度为n,是只有一行,n列,别搞混,有的说是n行1列式错误的),下一层的节点数为m(m < n),则权重矩阵W的维度为n×m,通过矩阵乘法实现从n维到m维的降维:
(下一层节点输出 = X* W + 偏置)
三、具体过程:以 “狗、猫、鸟分类” 为例
假设网络结构为:
卷积层→拉平→全连接层1(1024节点)→全连接层2(512节点)→输出层(3节点)
1. 拉平后→全连接层 1(从 12544 节点→1024 节点)
- 拉平后的输入向量X维度为 12544(即 12544 个特征值,来自卷积层的高阶特征);
- 全连接层 1 的权重矩阵W1维度为12544×1024(12544 行,1024 列);
- 计算过程:
全连接层 1 的每个节点(共 1024 个)的输出,是X与W1中对应列的权重进行 “加权求和” 后加偏置,再通过激活函数(如 ReLU)的结果:
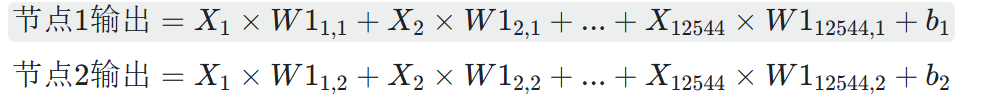
...(共 1024 个节点)
- 效果:通过 12544×1024 的权重矩阵,将 12544 维特征压缩为 1024 维,每个新节点都是原始特征的 “加权组合”(保留重要特征,丢弃冗余信息)。
2. 全连接层 1→全连接层 2(从 1024 节点→512 节点)
- 全连接层 1 的输出是 1024 维向量(1024 个特征值);
- 全连接层 2 的权重矩阵W2维度为1024×512;
- 计算过程:
全连接层 2 的每个节点(512 个)的输出,是全连接层 1 的 1024 个节点与W2对应列的权重进行 “加权求和” 后加偏置的结果:
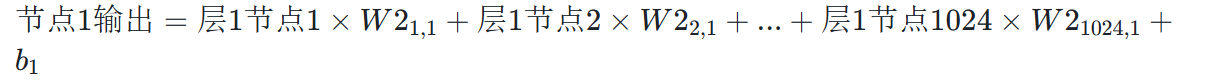
- 效果:进一步将 1024 维特征压缩为 512 维,通过权重矩阵筛选更核心的特征(如狗的 “圆润耳朵 + 4 条腿”、鸟的 “翅膀 + 2 条腿” 等关键组合)。
四、为什么要减少节点数?
- 降低计算量:全连接层的参数数量是上一层节点数×下一层节点数,12544×1024(约 1280 万参数)比 12544×512(约 640 万参数)计算量少一半,避免模型过于庞大。
- 防止过拟合:高维特征容易包含噪声(如狗图像的背景干扰),减少节点数相当于 “特征提纯”,让模型更关注通用规律(如狗的本质特征),而非训练数据的细节。
五、关键:节点数减少是 “人为设计 + 训练优化” 的结果
- 节点数减少的比例(如 12544→1024→512)是人为根据任务复杂度设定的(简单任务可减少更多,复杂任务保留更多);
- 权重矩阵W1、W2的具体值是通过训练学习的:网络会自动调整权重,让下一层节点优先 “放大” 对分类有用的特征(如狗的耳朵特征),“抑制” 无关特征(如背景噪声),从而在降维的同时不丢失关键信息。
总结
拉平后的全连接层通过权重矩阵的维度设计(上一层节点数 × 下一层节点数,下一层节点数更少)实现节点数减少。每个下一层节点都是上一层所有节点的 “加权组合”,通过训练优化权重,在压缩维度的同时保留关键特征(如狗、猫、鸟的核心识别特征),最终实现高效且鲁棒的分类。
