part1~2 神经网络基础

深度学习的优缺点

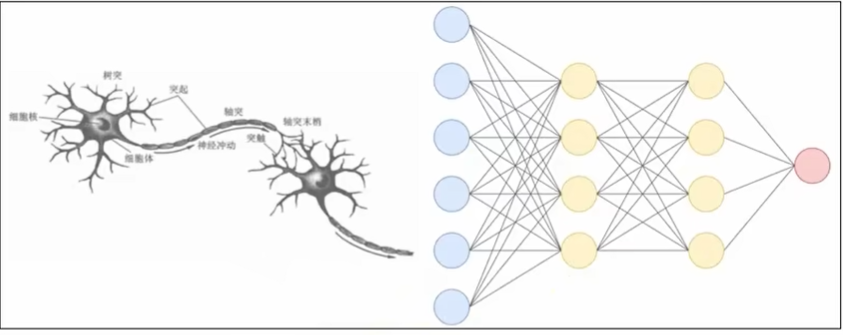
1.在深度学习中，特征工程很少提到了，使用多层神经网络，能够自动提取数据的多层次特征(特征选择，特征降维等)

2.适合处理非结构化数据，如图像，音频，文本等

3.依赖大量数据和计算资源，训练时间长

4.模型复杂，通常视为“黑盒”，可解释性差

神经网络构成

基本概念和结构

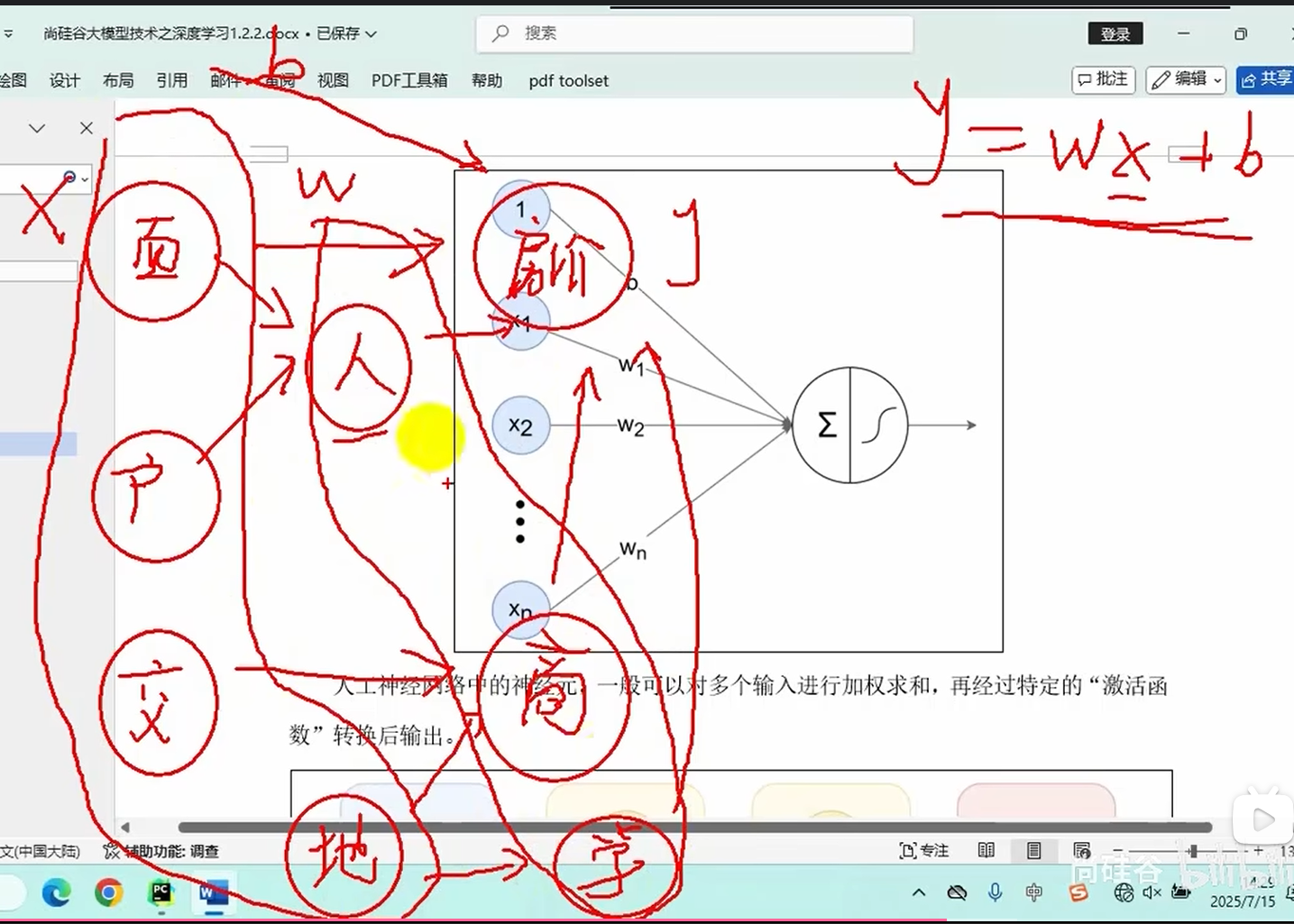
基本概念：就是线性回归的高级化（加了个激活函数），上述预测房价案例每个因素会影响房价也可能相互影响，导致构建起来繁琐，因此可以将所有因素进行分层处理

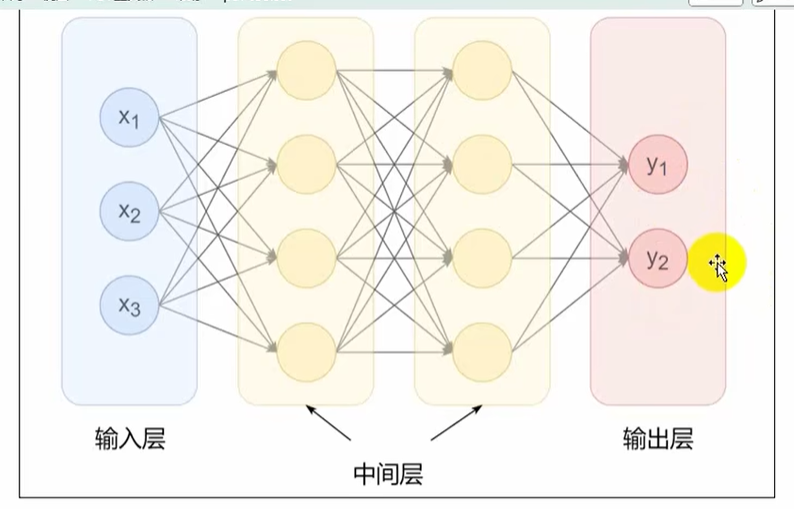
输入层：一个样例的n个特征(经过处理后的)

中间层(隐藏层)：就相当于特征处理

输出层：就是labels

相邻层的神经元相互连接，每个连接都会有一个权重

神经元中的信息逐层传递(一般称为前向传播forward),上一层神经元的输出作为下一层神经元的输入，

复习感知机和激活函数

感知机(Perceptron)是二分类模型，接收多个信号，输出一个信号（取值0 or 1）

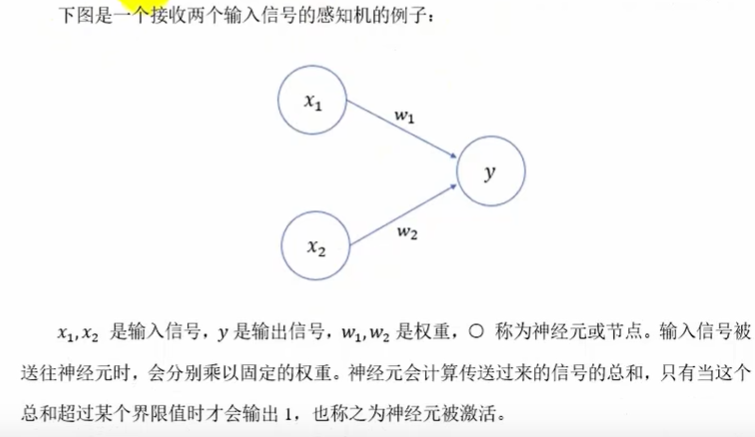
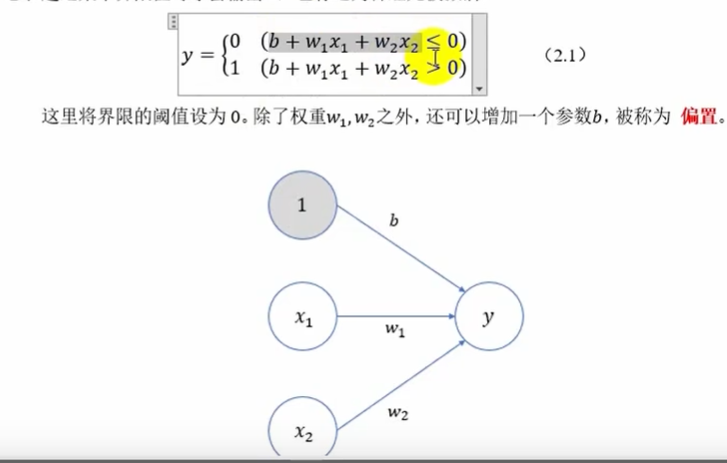
偏置值可以控制神经元被激活的难易程度

上例的阈值就是0，＞0输出1，＜0输出0

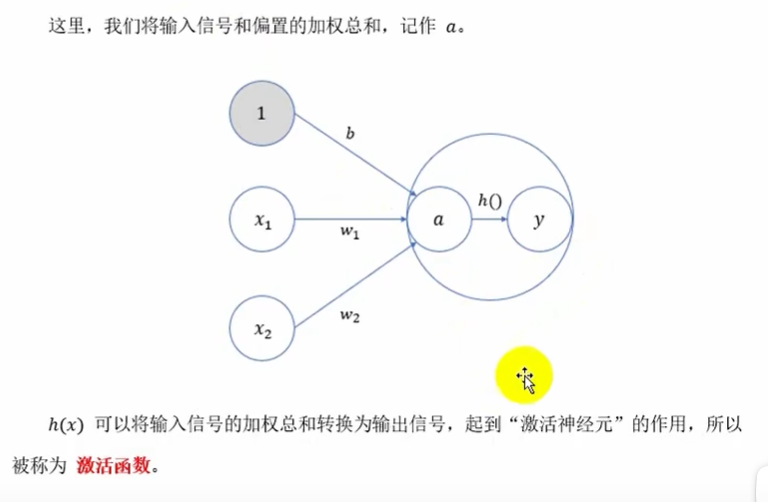
激活函数

激活函数的作用

激活函数就是连接感知机和神经网络的桥梁，激活函数是非线性的，如果没有激活函数，整个神经网络就等价于单层线性变换，

阶跃(binary step)函数

用途与创建

• ‌python软件包‌：用于代码复用和模块化（如数据分析库），通过pip install安装或手动创建含__init__.py的目录。‌‌
• ‌目录‌：用于非代码文件管理（如data/存放CSV文件），创建无需特殊文件。‌‌

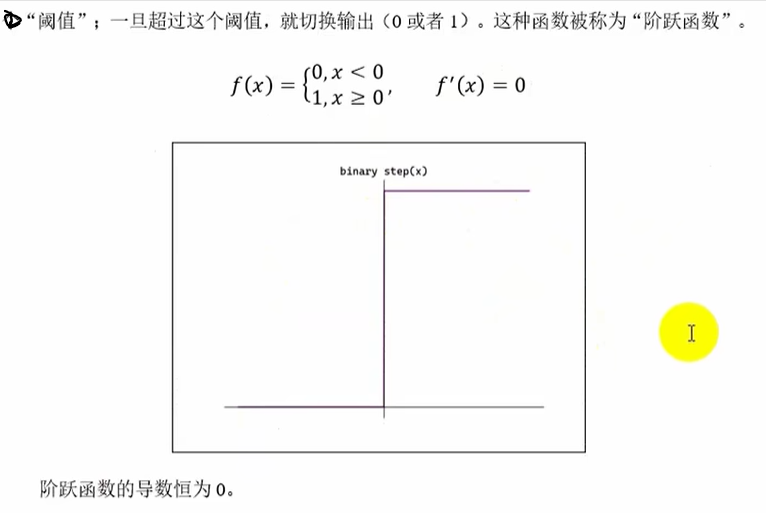
# 阶跃函数
def step_function0(x): # x就是输入的神经元加权和偏置的求和if x>0:return 1else:return 0
import numpy as np
def step_function(x):"""x>0:进行判断x中元素是否大于0，返回的是布尔值(True/False)并存入ndarray数组中dtype=int:将ndarray数组中的bool值转为int，True-->1 , False-->0"""return np.array(x>0,dtype=int)
"""
__name__ :是Python的内置变量，表示当前模块的名称
当一个Python文件直接运行时，__name__ 的值会被设置为 '__main__'
当一个Python文件被导入到其他模块时，__name__ 的值会是该文件的文件名（不含.py扩展名）
"""
if __name__=='__main__':x=np.array([0,1,2,3,4,5,-1,-2,-3,-4,-5])print(step_function(x)) # or print(step_function0(x))

运行结果：

Sigmoid函数(多用于分类输出层)

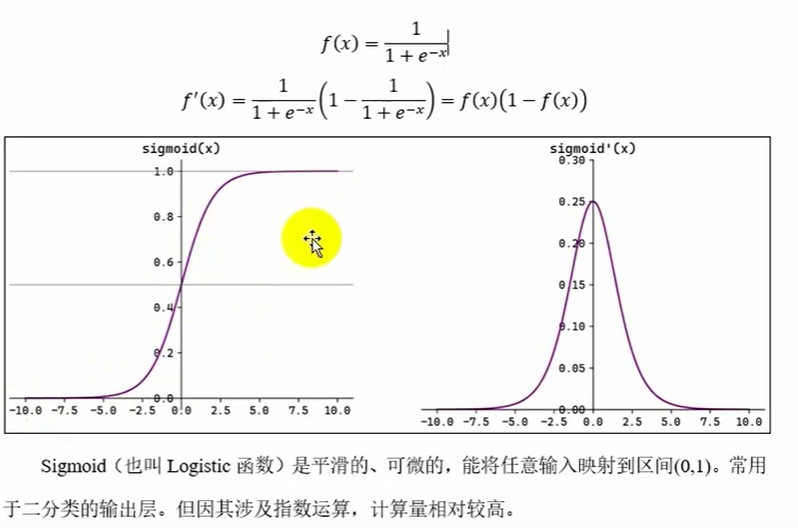
sigmoid函数关于(0,0.5)对称，一般用于输出层，若用于隐藏层，随着不断层数增大的不断使用，会出现梯度消失的情况(就是变成类似于线性变换且y'=0)

# Sigmoid函数：
def sigmoid(x):return 1/(1+np.exp(-x))
if __name__=='__main__':x=np.array([0,1,2,3,4,5,-1,-2,-3,-4,-5])print(sigmoid(x))

运行结果：

Tanh双曲正切函数(啥也不是，只适合浅层隐藏层)

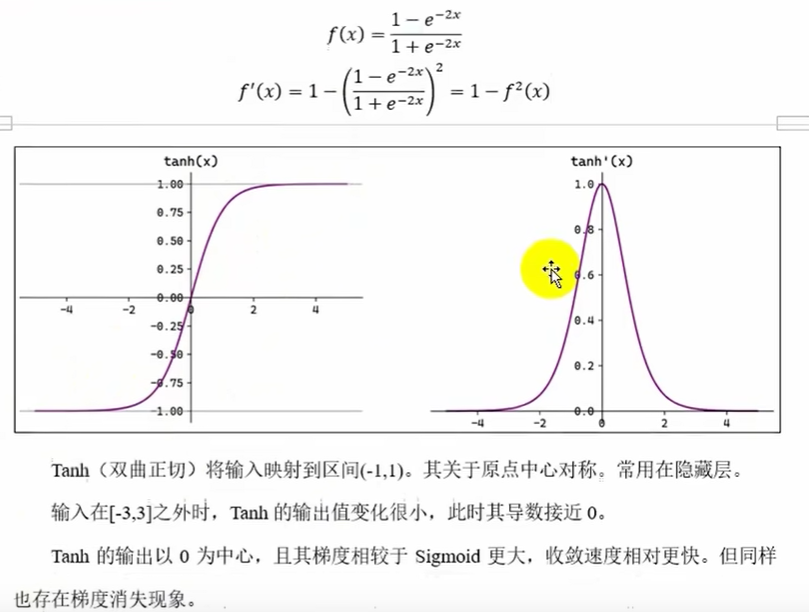
f(x)=2sigmoid(2x)-1 :sigmoid函数关于(0,0.5)对称，所以tanh函数关于(0,2*0.5-1)---(0,0)对称

由于是2x，所以相对于sigmoid函数，tanh梯度下降更快，但也会出现梯度消失，虽然一般用于隐藏层，但也不适合用于隐藏层，所以这个函数不好

# Tanh函数：就是2*Sigmoid(2x)-1
if __name__=='__main__':x=np.array([0,1,2,3,4,5,-1,-2,-3,-4,-5])print(np.tanh(x))print((2*sigmoid(2*x)-1))

运行结果:

ReLU函数(多用于隐藏层，不会梯度消失)

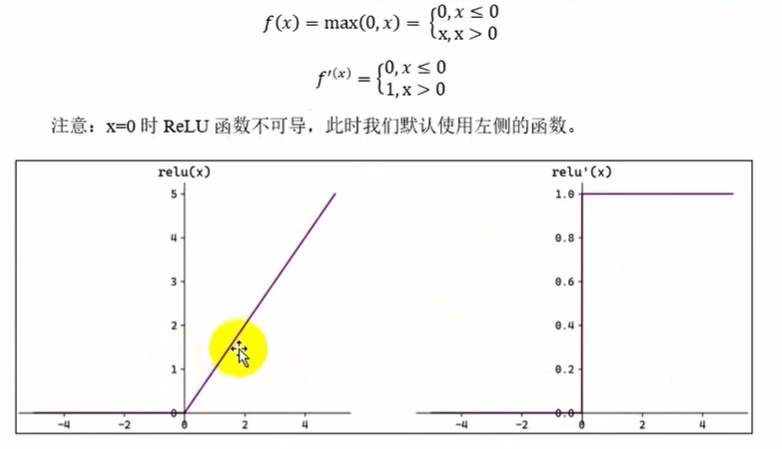
# ReLu函数
def ReLU(x):return np.maximum(0,x)
if __name__=='__main__':x=np.array([0,1,2,3,4,5,-1,-2,-3,-4,-5])print(ReLU(x))

运行结果：

Softmax函数(多用于分类输出层)

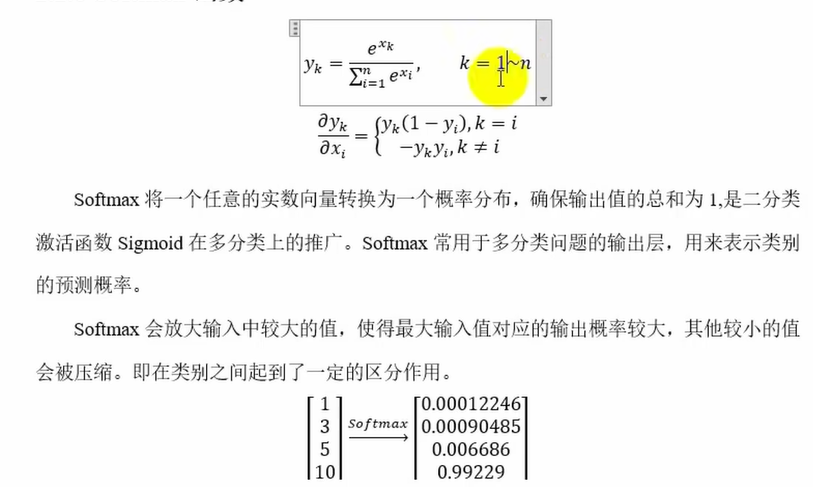
因为e^x相对于x在(0,1)导数小于1，(1,正无穷)随着x增大而增大，所以将x--->e^x可以使在整体中占的比例大的数再放大，小的数再缩小，在分类问题中起到了区分作用

二分类激活函数Sigmoid在多分类问题上的推广，适合多分类问题

# Softmax函数
def softmax0(x): # 只处理一条数据return np.exp(x)/np.sum(np.exp(x))
# 考虑输入可能是矩阵情况
def softmax(x):# 如果是二维矩阵if x.ndim==2:# 二维溢出处理x=x.T # x变成(3,4)x=x-np.max(x,axis=0) # np.max(x,axis=0)变成了(,4) 然后通过广播机制将(,4)-->(1,4)-->(3,4),最后进行溢出处理相减y=np.exp(x)/np.sum(np.exp(x),axis=0)return y.T# 一维溢出处理策略x=x-np.max(x)return np.exp(x)/np.sum(np.exp(x))
if __name__=='__main__':x=np.array([[0,1,2],[3,4,5],[6,7,8],[-1,-2,-3]])print(softmax(x))

运行结果：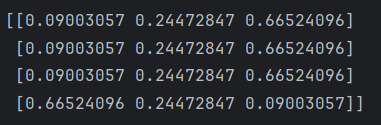

可以看成一个三分类，有四个样本，每一行是一个样本，每一行的三个数代表是那种东西的概率，合计为1

当 x 是一个二维数组时（例如形状为 (m, n)），np.sum(np.exp(x), axis=1) 会对每一行（共m行）的n个元素分别求和，得到一个形状为 (m,) 的一维数组

在除法运算时，NumPy的广播机制会发挥作用。指数化后的数组 np.exp(x) 形状仍为 (m, n)，而求和结果形状为 (m,)。为了进行逐元素除法，求和结果会被"广播"（即虚拟地扩展）成形状 (m, 1)---在列方向复制n次变成(m,n)，然后与 (m, n) 的数组相除，最终结果形状仍为 (m, n)

其他常见激活函数

identity(多用于回归输出层)

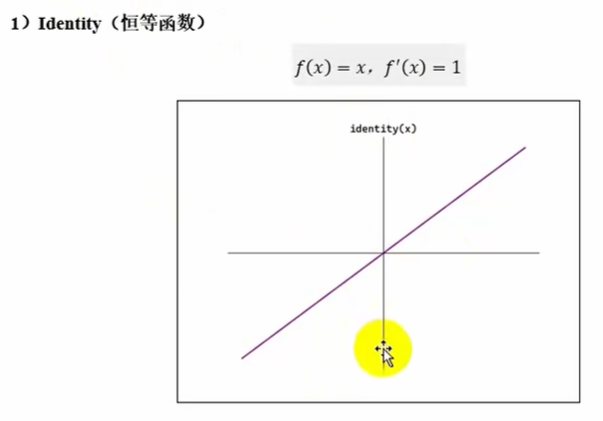
没有非线性，隐藏层不会用，可能在输出层用

Leaky ReLU(多用于输出层)

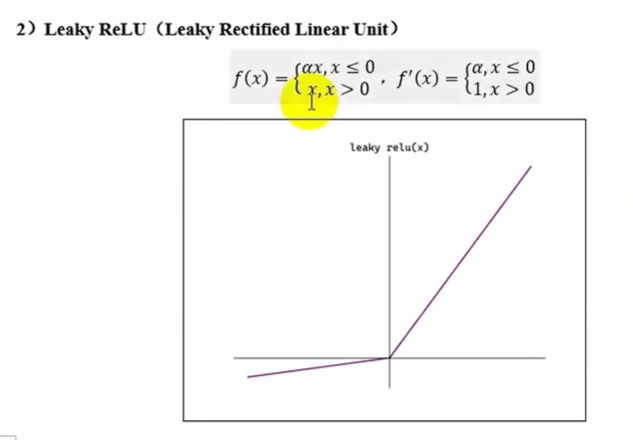
PReLU

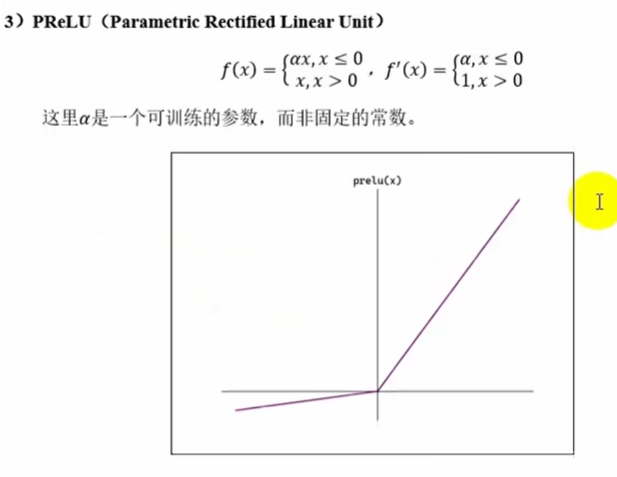
RReLU

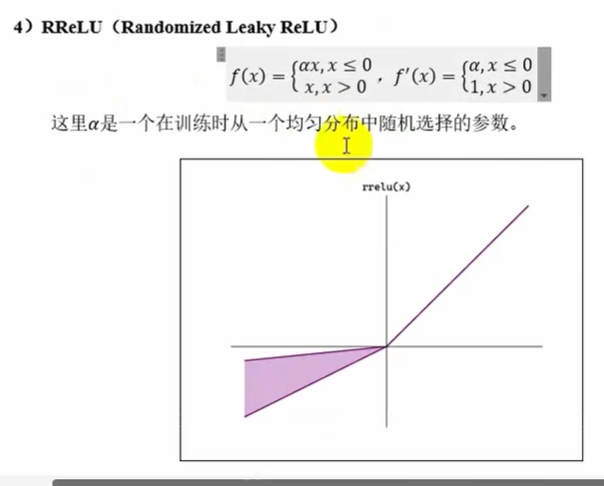
ELU

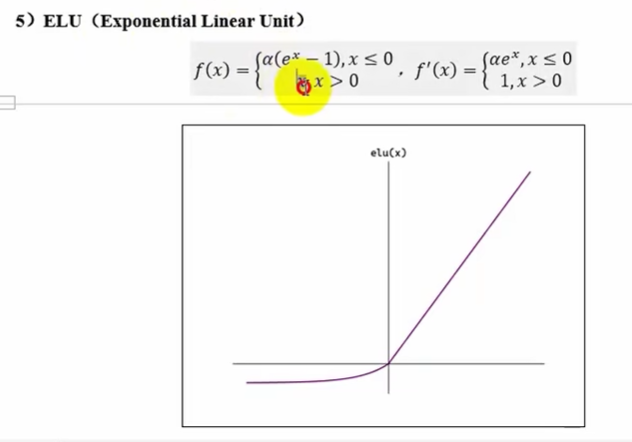
Swish

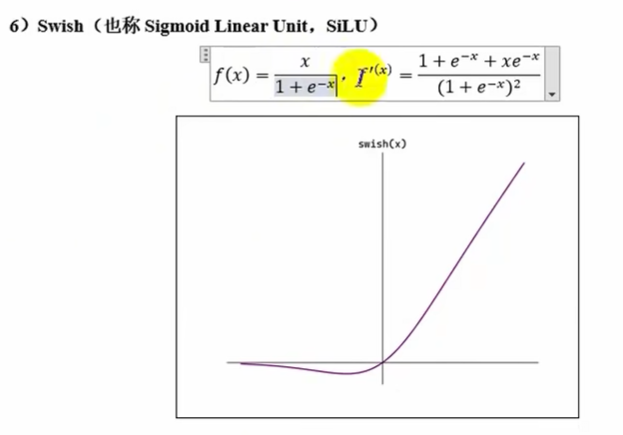
Softplus

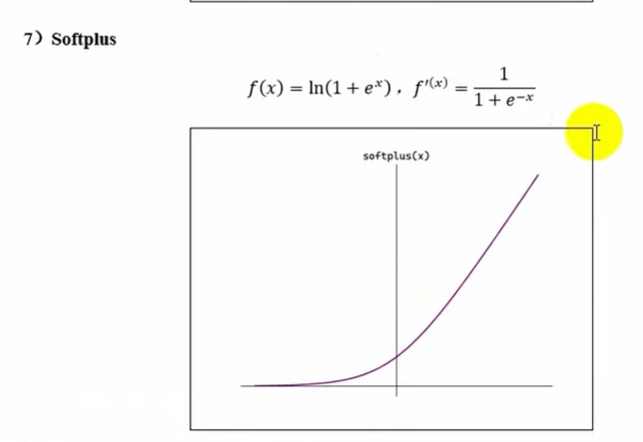
如何选择激活函数

神经网络的简单实现

深度神经网络由多个层(layer)组成，通常称为模型(model),每个模型接收原始输入(特征)，生成输出(预测)，并包含一些参数

三层神经网络

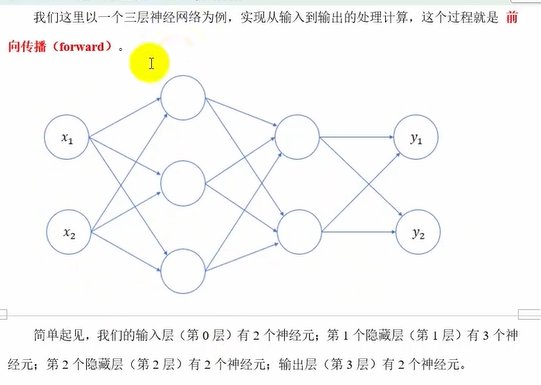
第0层(输入层)-->第1层

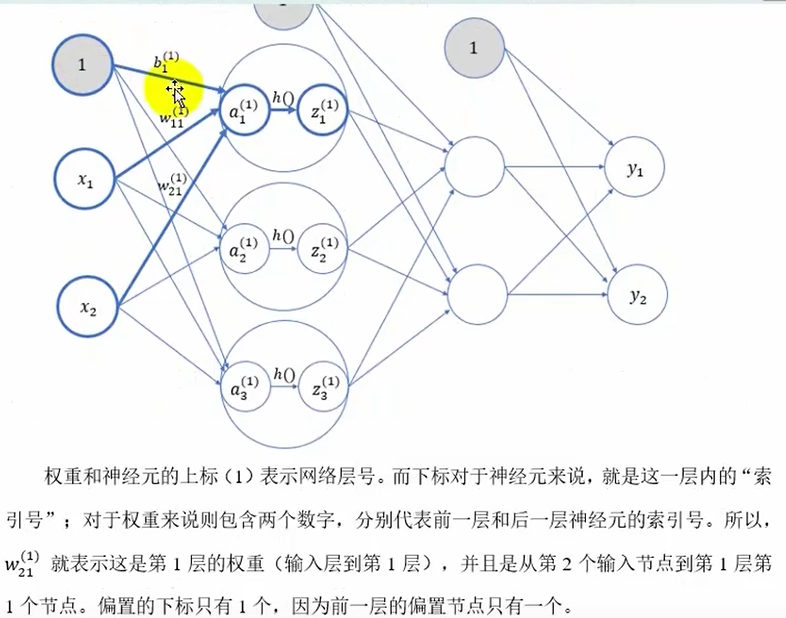
上标(1)表示网络层号，下标表示这一层内的索引号，如权重下标两个数字分别代表前一层和后一层神经元的索引号，偏置一个下标表示后一层的索引号

将输入写成行向量比较好--->A=XW+B

注意权重矩阵----一行代表从一个xi出发指向不同的下一层的xi

第1层-->第2层

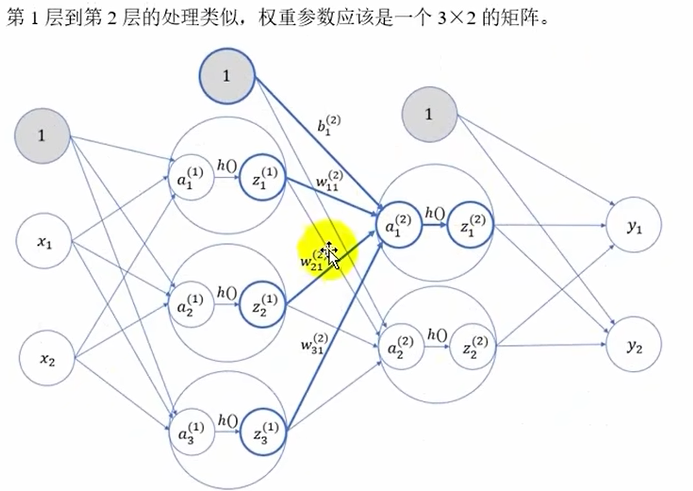
第2层-->第3层(输出层)

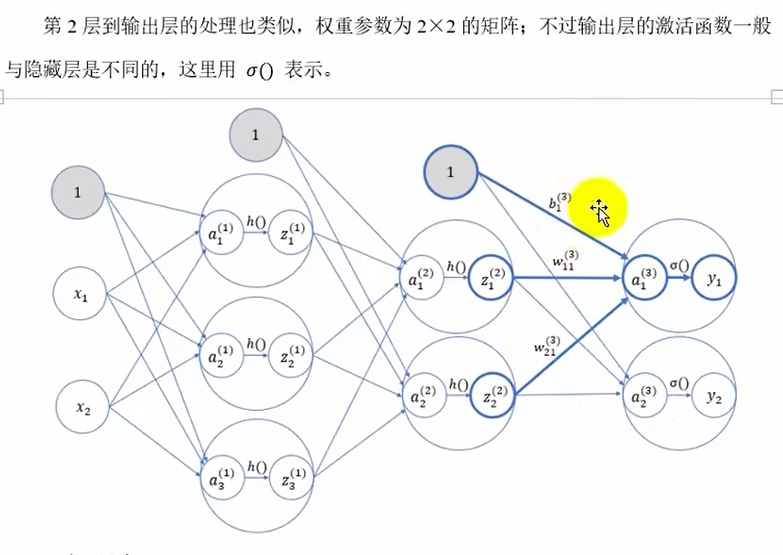
三层网络代码实现

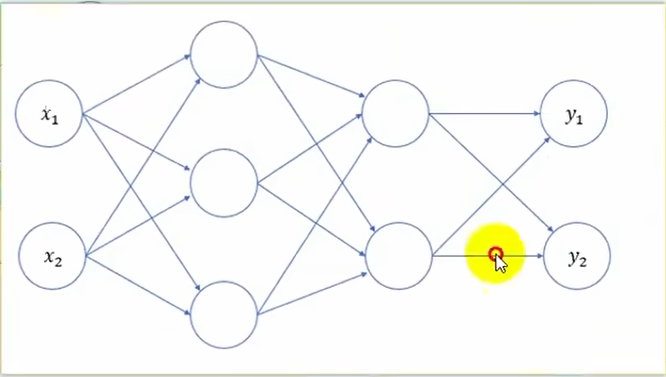
import numpy as np
from common.functions import sigmoid,identity
# 初始化网络(定义一个空的网络)
def init_network():network=dict() # 一个网络就是字典,权重的value是二维矩阵，偏置的value是一维数组# 第一层参数（value都是ndarray）network['W1']=np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]]) network['b1']=np.array([0.1,0.2,0.3])      # 其中W1是W(1),b1是b(1)---指从第0层到第一层# 第二层参数network['W2'] = np.array([[0.1,0.4], [0.2,0.5],[0.3,0.6]])network['b2'] = np.array([0.1, 0.2])# 第三层参数network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])network['b3'] = np.array([0.1, 0.2])return network
# 前向传播
def forward(network,x):w1,w2,w3=network['W1'],network['W2'],network['W3']b1,b2,b3=network['b1'],network['b2'],network['b3']# 逐层进行计算传递a1=np.dot(x,w1)+b1z1=sigmoid(a1)a2=np.dot(z1,w2)+b2z2=sigmoid(a2)a3=np.dot(z2,w3)+b3z3=identity(a3) # z3 is yreturn z3
# 测试主流程
network=init_network()
# 定义数据
x=np.array([1.0,0.5])
x=x.reshape(1,-1) # 将x的维度重塑为(1,所有数据的列)
# 前向传播(预测)
y=forward(network,x)
print(y)

运行结果：

注意：其中W1是W(1),b1是b(1)---指从第0层到第一层

案例：手写数字识别

https://www.kaggle.com/competitions/digit-recognizer

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
from common.functions import  sigmoid,softmax # 激活函数
import joblib
# 读取数据
def get_data():# 1.从文件内加载数据集dataframedata=pd.read_csv("../data/train.csv")# 2.划分数据集x=data.drop("label",axis=1) # axis=1是跨列y=data["label"]x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3,random_state=42)# 3.特征工程：归一化scaler=MinMaxScaler()x_train=scaler.fit_transform(x_train)x_test=scaler.fit_transform(x_test)return x_test,y_test # 不用返回x_train,y_train，本例子默认训练好了
# 初始化神经网络
def init_network():# 直接从文件中加载字典对象network=joblib.load("../data/nn_sample")return network
# 前向传播
def forward(network,x):w1,w2,w3=network['W1'],network['W2'],network['W3'] # ndarray数组b1,b2,b3=network['b1'],network['b2'],network['b3']# 逐层进行计算传递a1=np.dot(x,w1)+b1z1=sigmoid(a1)a2=np.dot(z1,w2)+b2z2=sigmoid(a2)a3=np.dot(z2,w3)+b3z3=softmax(a3) # z3 is yreturn z3
# 主流程
# 1.获取测试数据
x,y=get_data()
print(x.shape) # (12600, 784)
print(y.shape) # (12600,)
# 2.创建模型（加载参数）
network=init_network()
# 3.前向传播(测试)
y_proba=forward(network,x)
print(y_proba.shape) # (12600, 10) 12600条数据，每个数据有十个预测概率
# 4.将分类概率转换为分类标签
y_pred=np.argmax(y_proba,axis=1) # (12600,)
print(y_pred.shape)
# 5.计算准确率
accuracy_cnt=np.sum(y_pred==y)
n=x.shape[0]
print("当前准确率accuracy_cnt:",accuracy_cnt/n)

运行结果：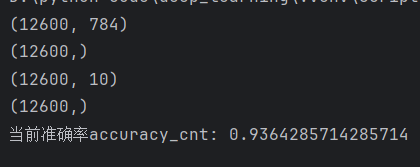

若数据量太大，计算处理不了，将数据分小批次处理并计算：

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
from common.functions import  sigmoid,softmax # 激活函数
import joblib
# 读取数据
def get_data():# 1.从文件内加载数据集dataframedata=pd.read_csv("../data/train.csv")# 2.划分数据集x=data.drop("label",axis=1) # axis=1是跨列y=data["label"]x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3,random_state=42)# 3.特征工程：归一化scaler=MinMaxScaler()x_train=scaler.fit_transform(x_train)x_test=scaler.fit_transform(x_test)return x_test,y_test # 不用返回x_train,y_train，本例子默认训练好了
# 初始化神经网络
def init_network():# 直接从文件中加载字典对象network=joblib.load("../data/nn_sample")return network
# 前向传播
def forward(network,x):w1,w2,w3=network['W1'],network['W2'],network['W3'] # ndarray数组b1,b2,b3=network['b1'],network['b2'],network['b3']# 逐层进行计算传递a1=np.dot(x,w1)+b1z1=sigmoid(a1)a2=np.dot(z1,w2)+b2z2=sigmoid(a2)a3=np.dot(z2,w3)+b3z3=softmax(a3) # z3 is yreturn z3
# 主流程
# 1.获取测试数据
x,y=get_data()
print(x.shape) # (12600, 784)
print(y.shape) # (12600,)
# 2.创建模型（加载参数）
network=init_network()
# 定义变量
batch_size=100
accuracy_cnt=0
n=x.shape[0] # 总数据量
# 3.循环迭代：分批次测试，前向传播，并累积预测准确个数
for i in range(0,n,batch_size):# 3.1取出当前批次数据x_batch=x[i:i+batch_size] # 左闭右开# 3.2前向传播y_batch_proba=forward(network,x_batch) # (100,10)# 3.3将输出分类概率转换为分类标签y_pred=np.argmax(y_batch_proba,axis=1)# 3.4累加准确个数accuracy_cnt += np.sum(y_pred==y[i:i+batch_size])
# 4.计算准确率
print("当前准确率accuracy_cnt:",accuracy_cnt/n)

运行结果：