各种各样的Self-attention学习下(第二十一周周报)
摘要
本文系统性地阐述了优化自注意力机制计算效率的核心思路与方法。文章首先指出标准自注意力N×N矩阵存在低秩冗余,并介绍了Linformer等模型通过线性投影压缩键/值序列来利用这一特性。接着,文章探讨了通过筛选或聚合来减少键或查询的数量,从而直接缩小注意力矩阵规模的方法。
文章的重点在于揭示自注意力计算的数学本质,并展示如何通过改变计算顺序来优化。通过公式推导,文章阐明可以将昂贵的“逐个交互再求和”过程,转变为“先总和再交互”的策略。即预先将序列中所有键和值的信息聚合为一个全局的“上下文概要”,此后每个查询只需与该概要进行一次交互即可得到输出。这种计算复用的策略避免了重复计算,是实现线性复杂度的关键。最后,文章通过示意图直观对比了这种高效计算范式与标准计算的差异。
Abstract
This article systematically explains the core concepts and methods for optimizing the computational efficiency of the self-attention mechanism. It begins by highlighting the low-rank redundancy inherent in the standard N×N self-attention matrix and introduces models like Linformer that leverage this property through linear projection to compress the key/value sequences. The article then explores methods to directly reduce the scale of the attention matrix by reducing the number of keys or queries via selection or aggregation.
A central focus is the mathematical underpinning of self-attention and how optimization can be achieved by changing the order of computation. Through formulaic derivation, the article demonstrates how the costly process of "interacting with each element and then summing" can be transformed into a strategy of "aggregate first, then interact." This involves pre-computing a global "context summary" by aggregating information from all keys and values in the sequence. Subsequently, each query only needs to interact with this summary once to produce its output. This strategy of computational reuse avoids redundant calculations and is key to achieving linear complexity. Finally, schematic diagrams are used to visually contrast this efficient computational paradigm with the standard approach.
目录
1 N×N是否冗余
2 Self attention运作,解释是否冗余
3 总结
1 N×N是否冗余
标准的多头自注意力矩阵虽然是 N×N 的大小,但本质上是低秩(Low Rank) 的,这意味着它包含大量冗余信息,可以被有效地压缩。
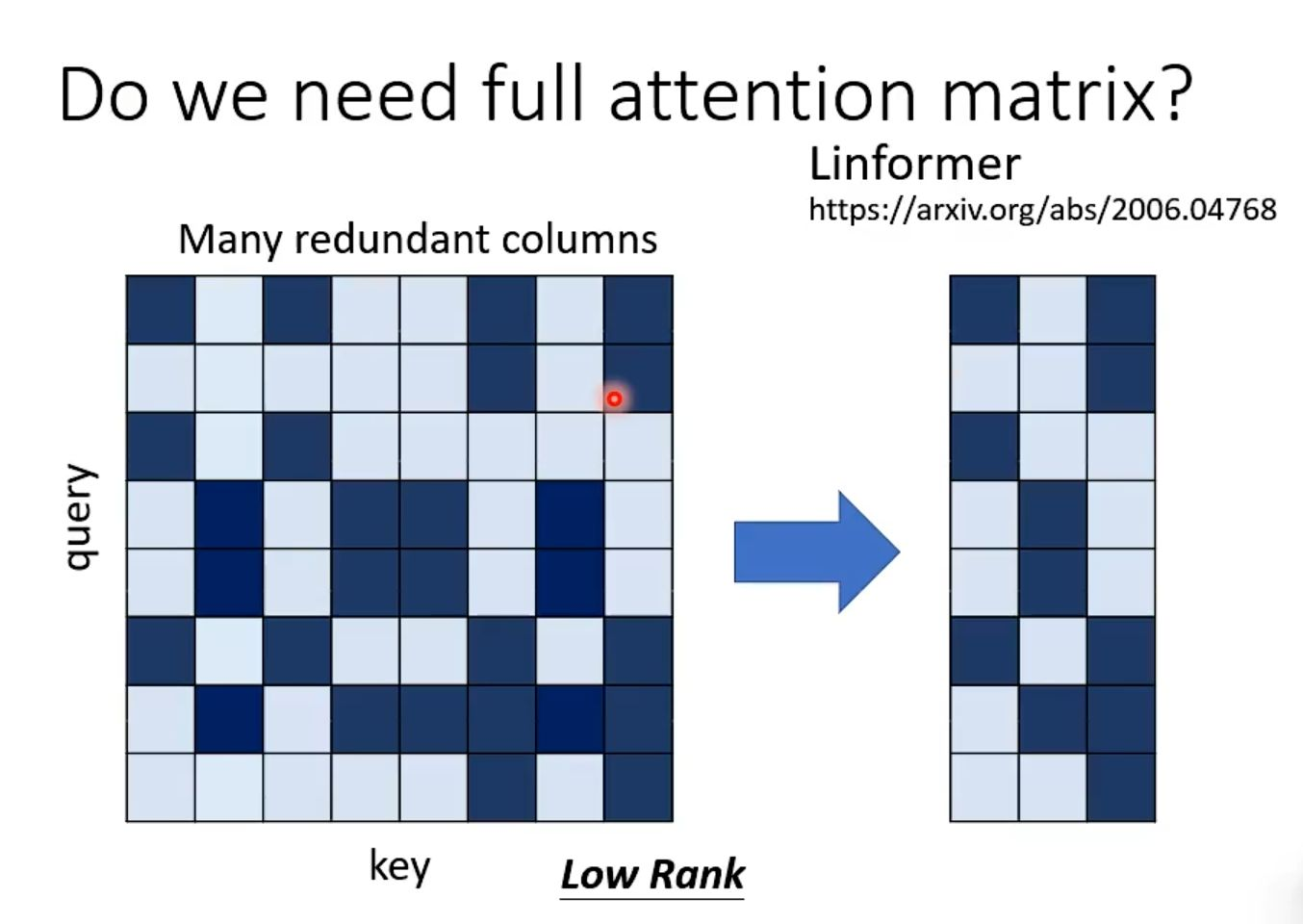
Linformer 的创新在于,它不再直接计算和存储庞大的 N×N 矩阵,而是通过对键(Key)和值(Value)序列进行线性投影,将它们从长度 N 映射到一个低维空间(例如长度 k,k << N)。这样,注意力计算的核心就变成了在一个 k 维空间中进行,从而将计算复杂度从序列长度 N 的平方量级成功地降低到了线性量级。简而言之,该图论证了我们并不需要完整的、稠密的注意力矩阵,利用其内在的低秩特性进行压缩是提升效率的有效途径。
减少查询成功是case by case的。减少查询数量来优化自注意力计算效率的核心思想。其关键在于改变输出序列的长度,从而大幅降低计算复杂度。
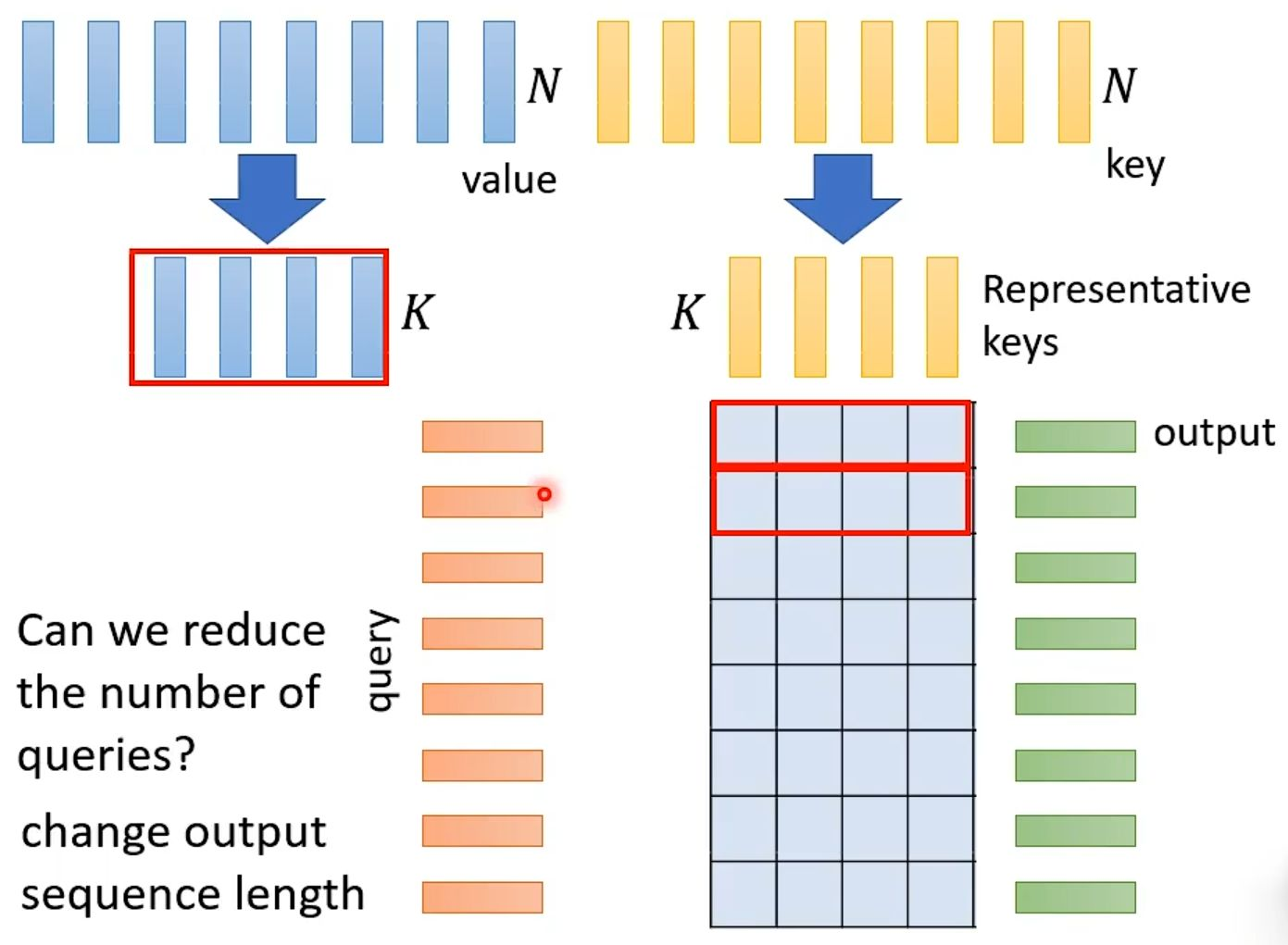
具体而言,该方法首先对原始序列中数量为N的键进行筛选或聚合,得到K个具有代表性的关键键。与此同时,查询的数量也不再与输入序列长度N强绑定,而是对应地减少到K个。这样,原本需要在N个查询和N个键之间计算的、规模为N×N的注意力矩阵,就被简化为在K个查询和K个代表性键之间进行计算。
减少要选出代表性的KEY。优化自注意力计算效率的核心方法如下所示。
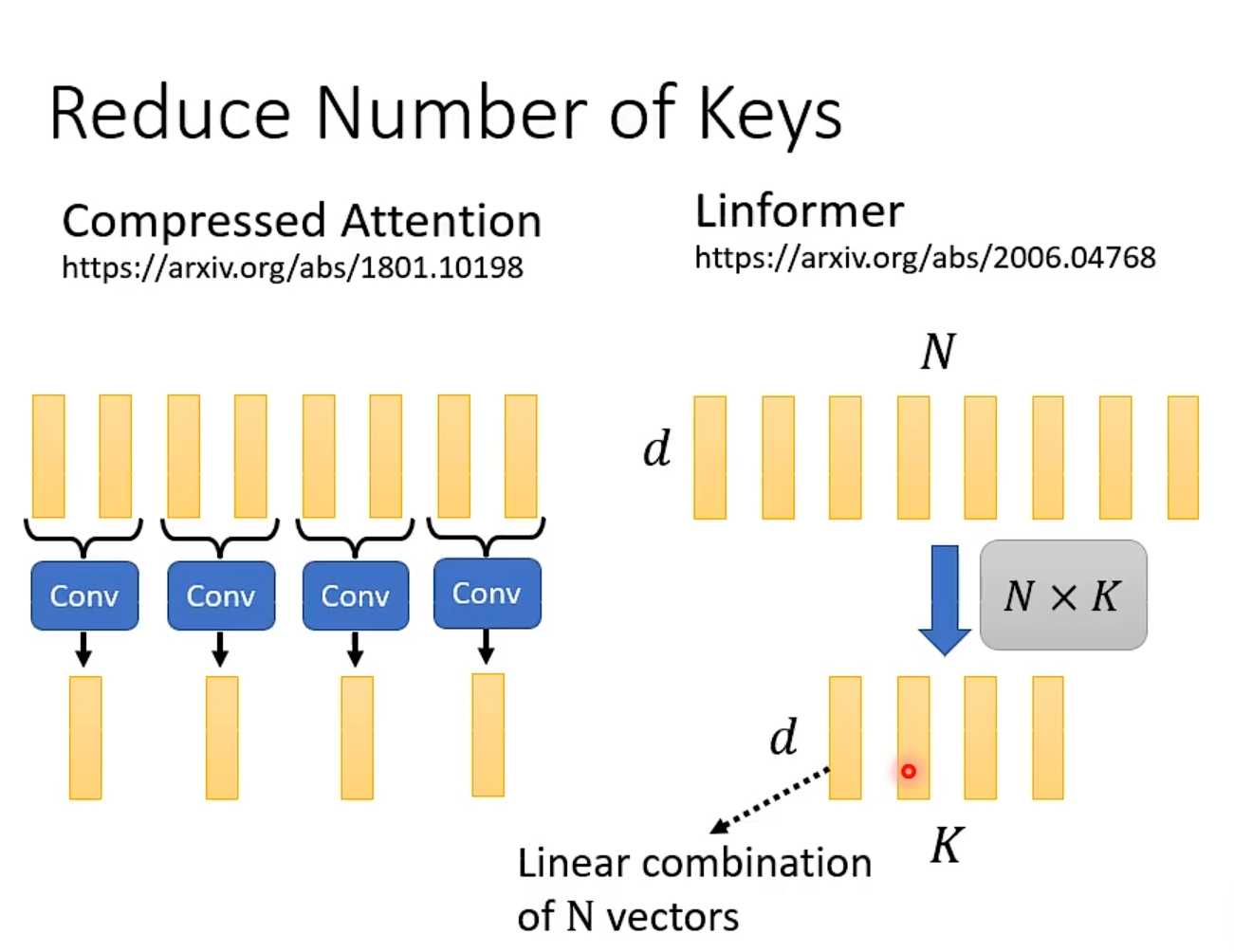
图左侧是 Compressed Attention 的方法,它通过对原始的 N 个键(Key)向量进行卷积(Conv)等操作,将它们压缩或聚合为数量更少的一组代表性键。图右侧是 Linformer 模型采用的核心技术,它通过一个线性投影(图中 “Linear combination of N vectors” 和 “N×K” 的矩阵表示),将长度为 N 的序列直接映射到一个长度为 K(K << N)的低维表示。
2 Self attention运作,解释是否冗余
计算注意力权重(图中以 α 表示)。具体来说,一个位置的查询向量(如 q¹)会分别与所有位置的键向量(如 k¹, k², ...)进行点积运算,并通过 Softmax 函数进行归一化,从而得到一系列权重分数(如 α‘₁,₁)。这些权重分数代表了在计算当前节点的输出时,应该“关注”或“分配”多少重要性给序列中的其他每个节点。
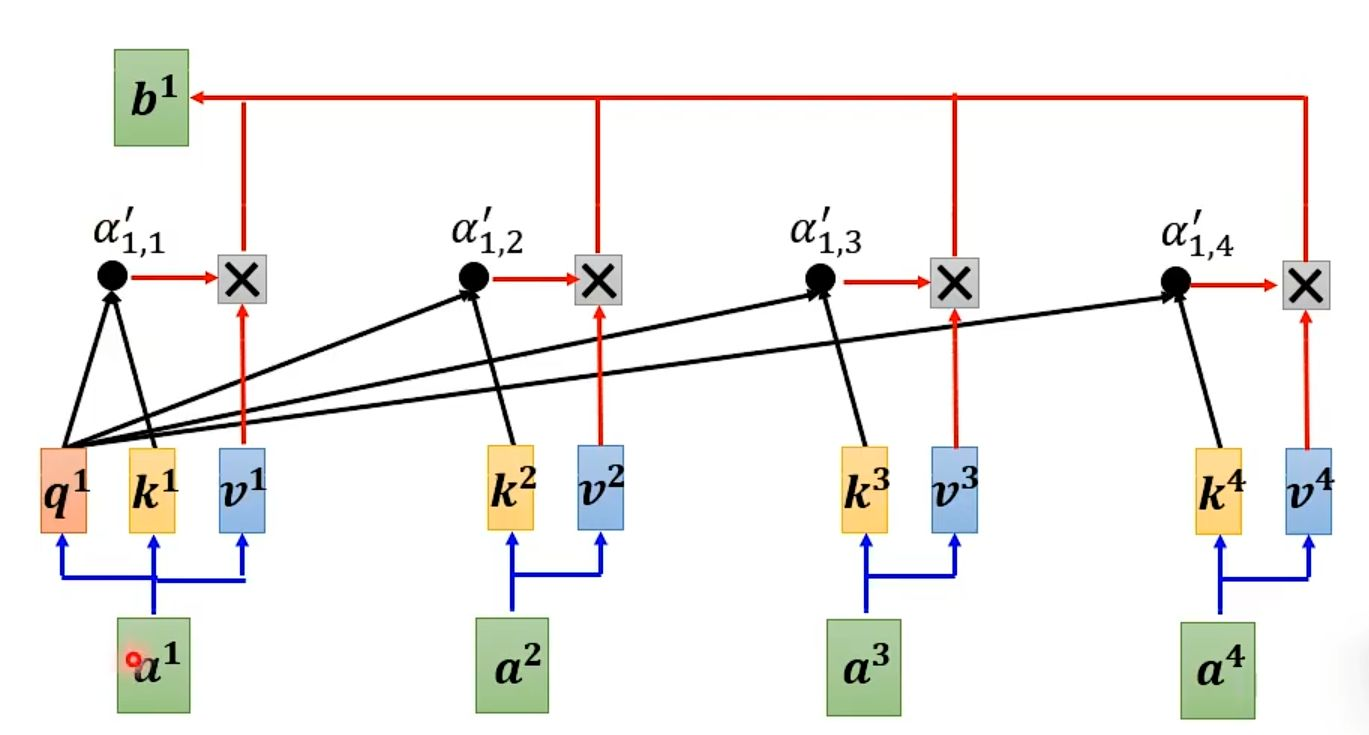
由公式如下图所示。可以看到比较麻烦,但是我们可以拆解一下。

化简之后,单独拎出来b1可以得到。

我们先观察比较简单的分母。

可以发现左半部分可以是两个矩阵相乘。我们再观察分子。
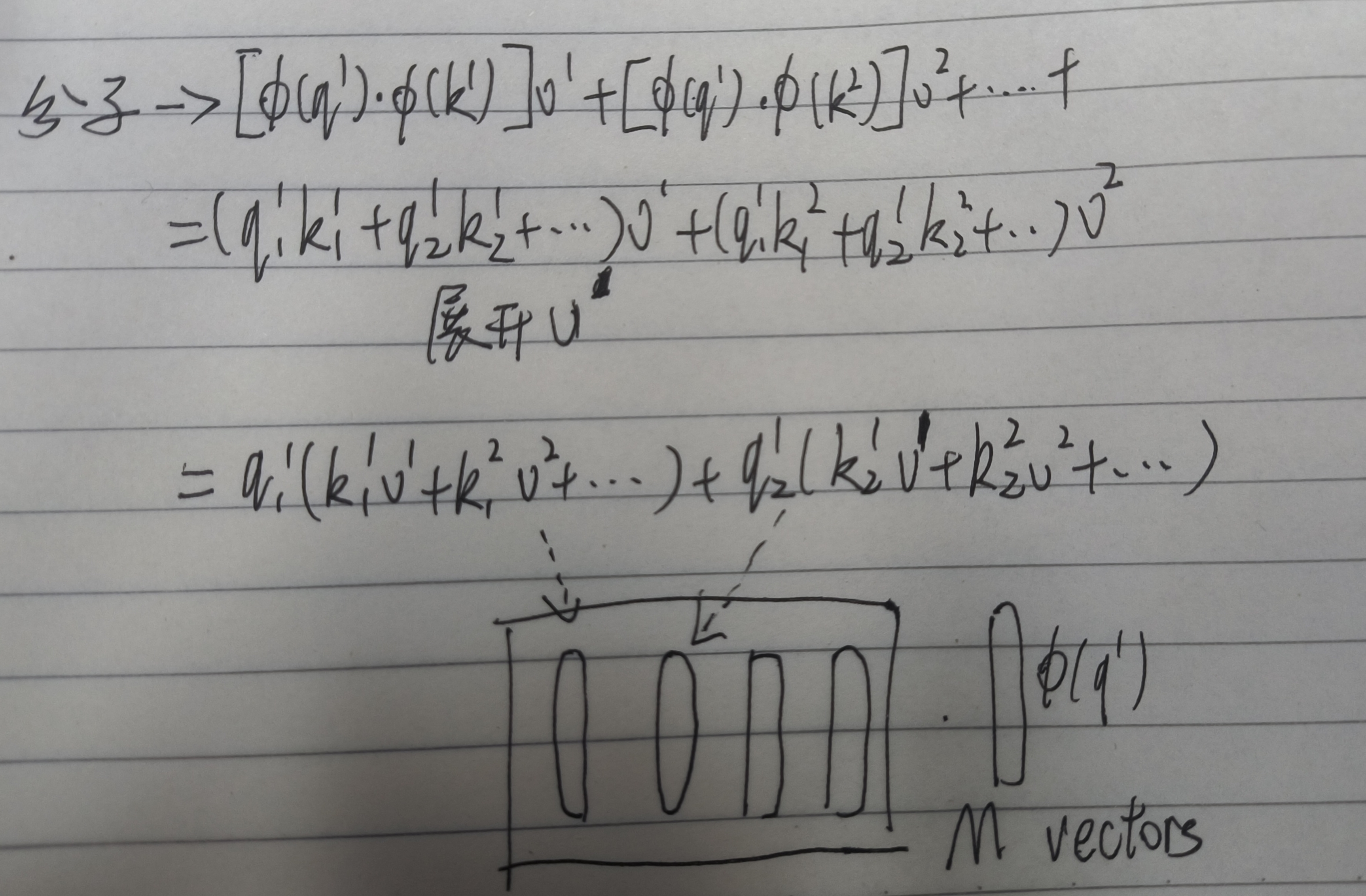
将昂贵的“查询-键”交互与“值”的加权求和这两个步骤分离开。通过先聚合所有键值信息,再让查询与该聚合结果交互,避免了序列长度的平方次计算,从而实现了线性复杂度。
用形象的图可以得知,左侧无需再次进行计算。
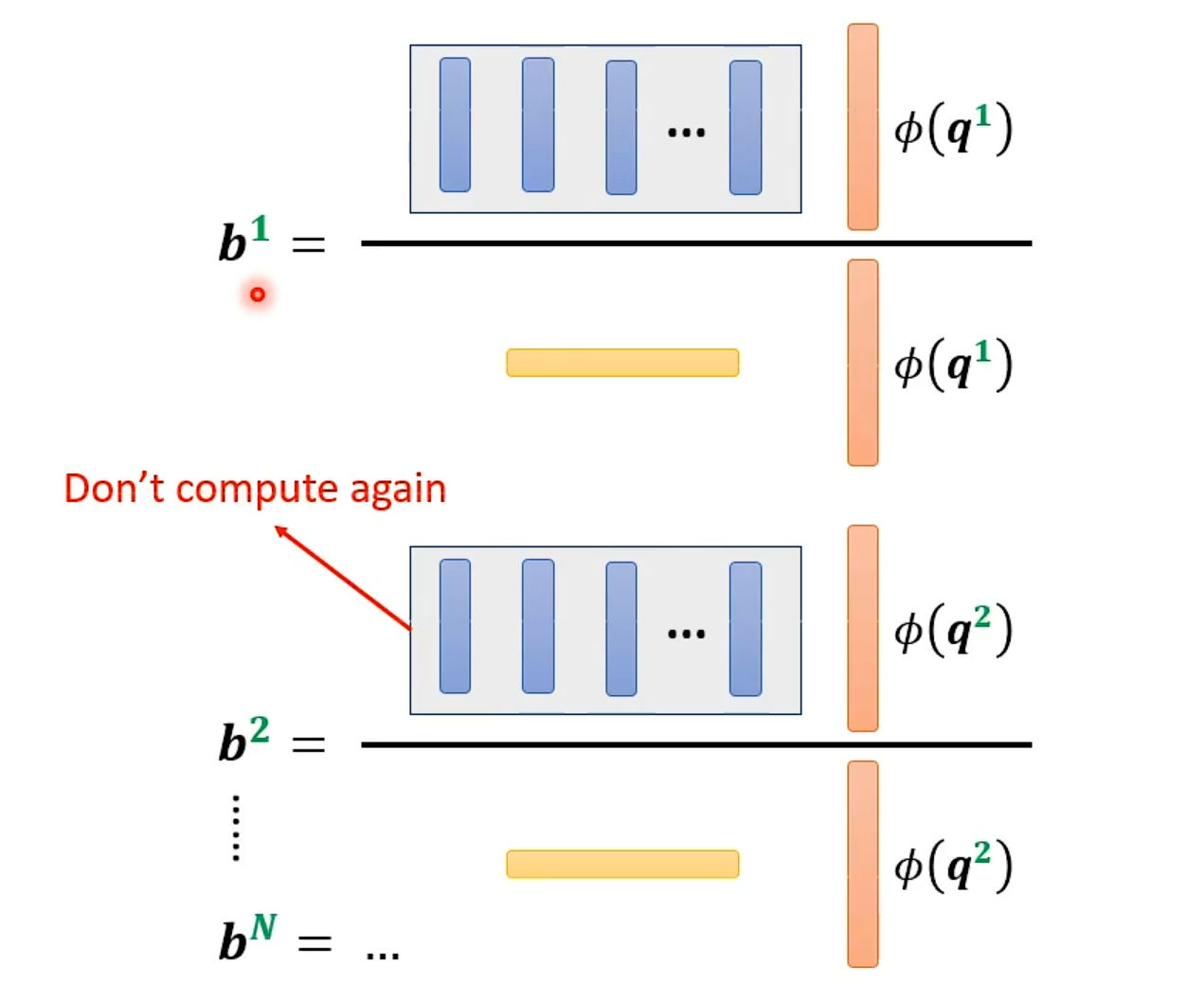
我们不需要为每个查询(如 φ(q¹) 和 φ(q²))都独立地、重复地计算这个公共模块。相反,这个复杂的中间结果只需要被计算一次,然后就可以被缓存起来,供序列中所有位置的查询计算时复用。
我们再来看老师的,更加简便的计算方式。
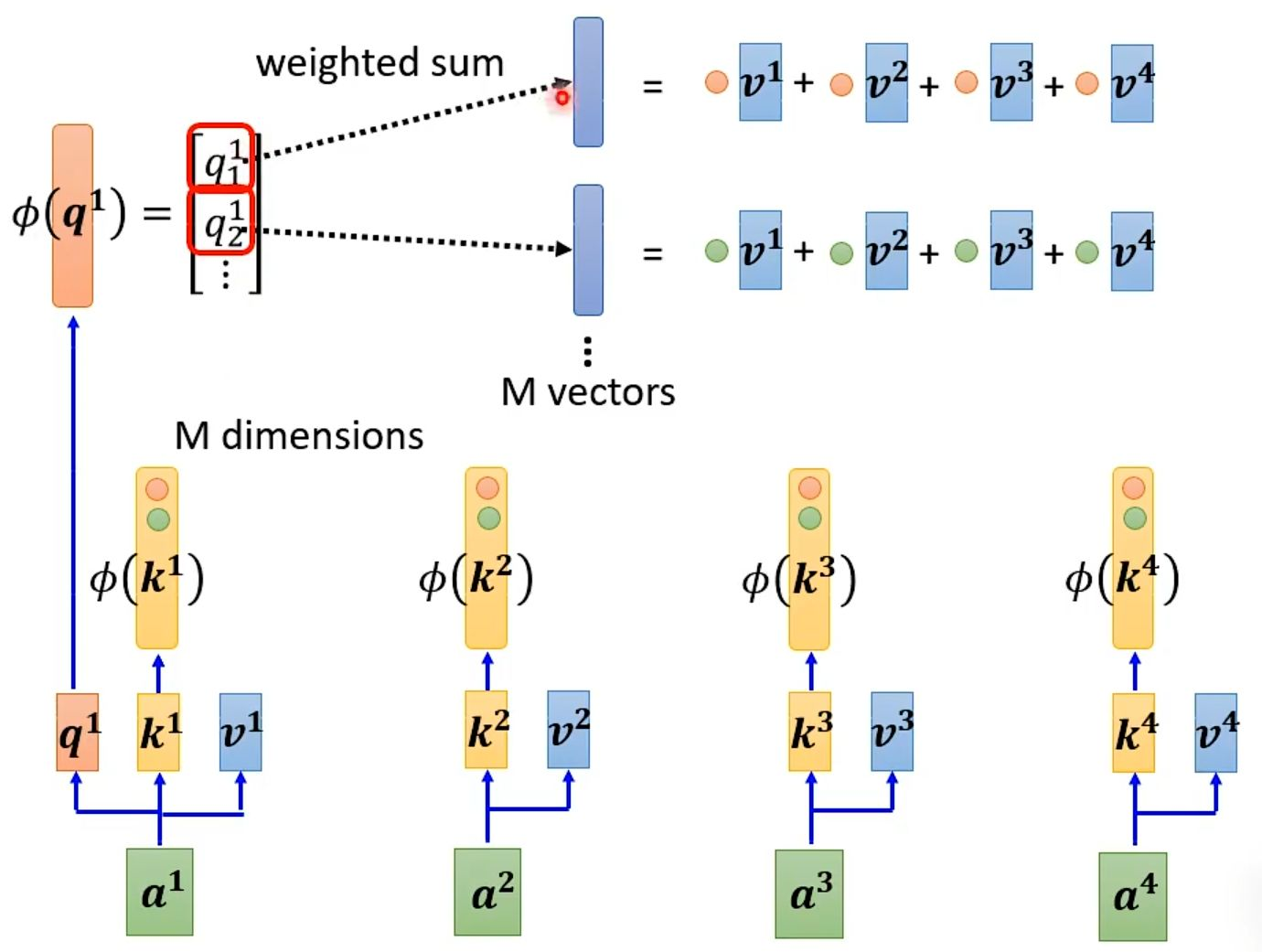
一个查询向量 q¹ 通过函数 φ 进行映射,然后将映射后的结果 φ(q¹) 与一组已经预先计算好的“键-值”聚合向量进行简单的点积操作,从而直接得到输出。这个聚合向量是图中的关键,它由下方的 M 个向量(代表序列中所有位置的信息)汇总而成。
具体来说,这个高效过程分为两步:
预先聚合:模型会先将序列中所有位置的键向量 φ(kⁱ) 和对应的值向量 vⁱ 进行加权组合,形成一个全局的“上下文概要”或“记忆库”。这一步只需要对整个序列做一次。
快速查询:当需要计算某个位置(例如 q¹ 对应的位置)的输出时,只需将映射后的查询 φ(q¹) 与这个预先聚合好的“上下文概要”进行一次性交互即可,而无需再与序列中的每一个键逐个比较。
这种将“逐个交互再求和”转变为“先总和再交互”的策略,避免了昂贵的 N×N 注意力矩阵计算,使得模型即使处理极长序列也能保持高效。图中下方的 M 个向量及其连接线,正形象地表示了所有输入信息被压缩到这个高效的聚合结构中。
q2也是如此。
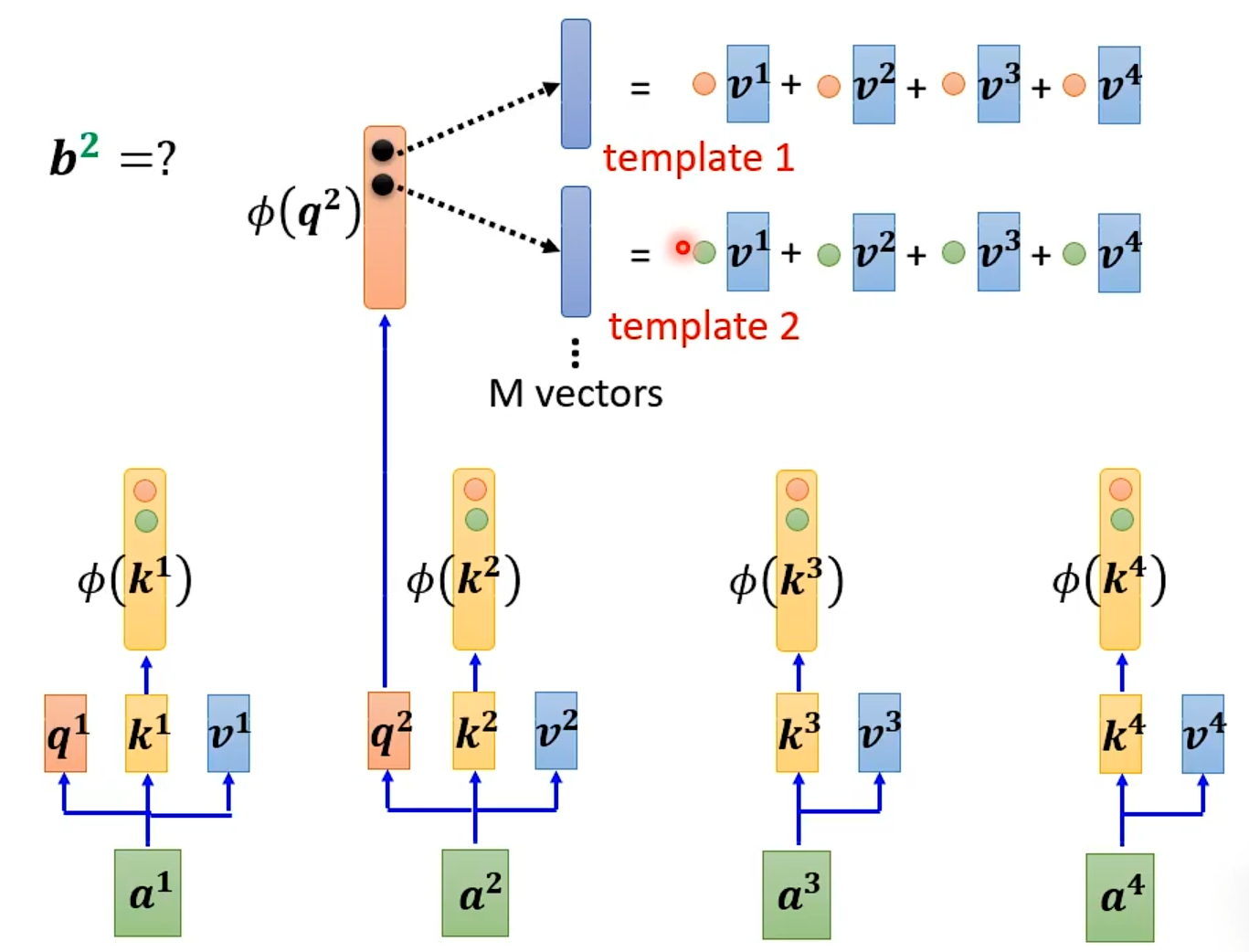
3 总结
高效自注意力的实现主要依赖于两大策略:规模缩减:通过低秩近似或筛选/聚合,直接减少参与计算的键或查询的数量,从源头上缩小问题规模。计算优化:利用数学恒等式改变计算顺序,将核心计算步骤转化为可被所有查询复用的公共操作,通过“预先聚合,一次性查询”避免重复的逐点计算。本质上是将计算复杂度从O(N²)降至O(N)的不同技术路径。
