【C++】位运算算法习题

🎆个人主页：夜晚中的人海

今日语录：梦想不是空口无凭的大话，而是在寂静的奋斗里努力生长的果实！

⭐一、判断字符是否唯一

题目链接：判断字符是否唯一

题目描述：

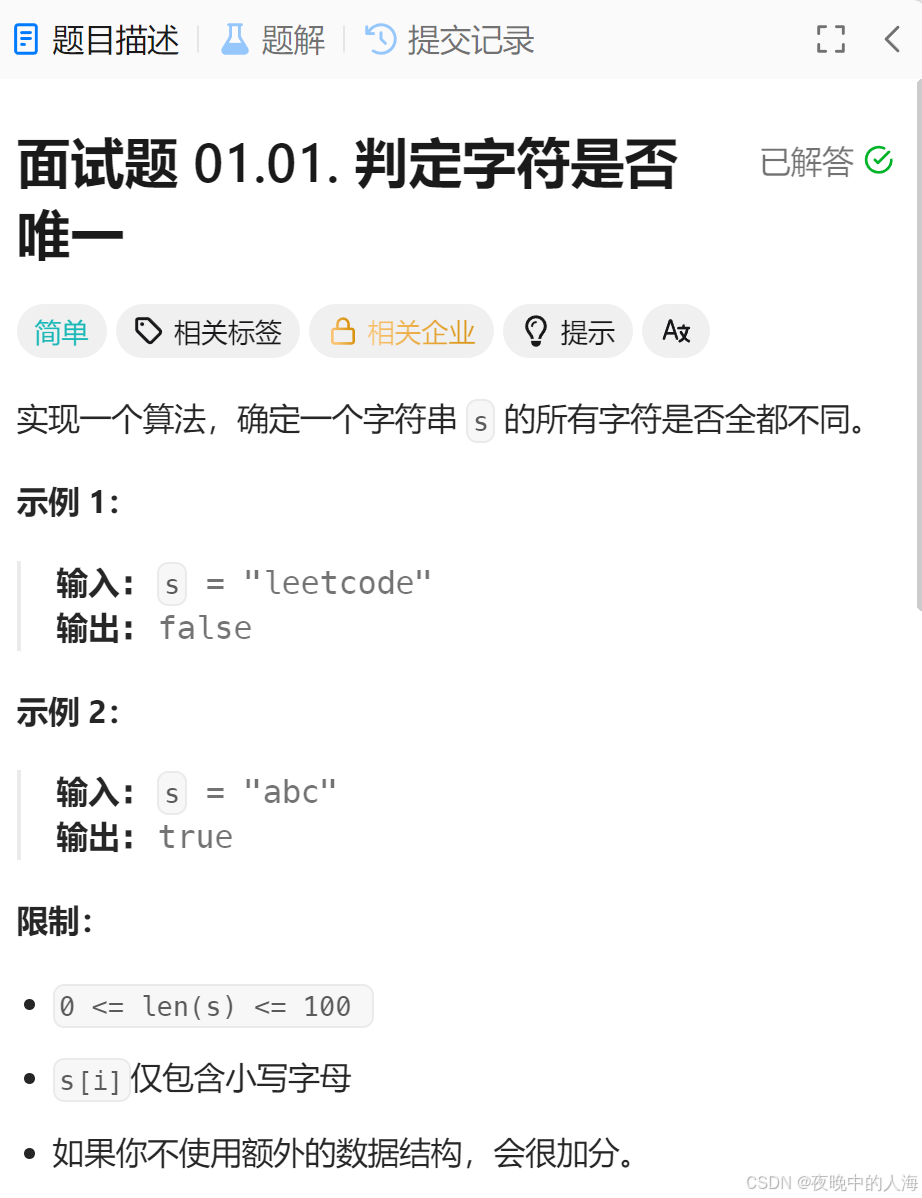
解题思路：
1.解法一：我们可以使用哈希表，记录当前字符出现的个数，如果大于1，则返回false，否则返回true

2.解法二：利用位图的思想，每一个比特位代表一个字符和一个int类型大小的字节表示所有的小写字母，比特位里面如果都为0，代表第一次出现该字符，为1，则表示该字符已经出现过

代码实现：

class Solution {
public:bool isUnique(string astr) {if(astr.size() > 26)return false;int bitmap = 0;for(auto ch : astr){int i = ch - 'a';//说明之前已经出现过了if(((bitmap >> i) & 1) == 1)return false;//把当前字符加入到位图中bitmap |= 1 << i;}return true;}
};

🏖️二、丢失的数字

题目链接：丢失的数字

题目描述：

解题思路：
1.我们设数组的大小为n，那么缺失的数据范围就在[0,n]之间

2.我们将数组中所有的数以及[0，n]之间所有的数都异或起来，根据异或运算消消乐的规则（相同的数字会被干掉），我们就可以求出那唯一一个消失的数字

代码实现：

class Solution {
public:int missingNumber(vector<int>& nums) {int n = nums.size();int ret = 0;for(auto num : nums){ret ^= num;}for(int i = 0;i <= n;i++){   ret ^= i;}return ret;}
};

🏝️三、两整数之和

题目链接：两整数之和

题目描述：

解题思路：
1.我们可以使用异或运算（本质：无进位加法）

2.使用按位与&操作得到进位

3.不断重复上述操作直至进位为0

代码实现：

class Solution {
public:int getSum(int a, int b) {while(b){int x = a ^ b;int j = (a & b) << 1;a = x;b = j;}return a;}
};

🚀四、只出现一次的数字II

题目链接：只出现一次的数字II

题目描述：

解题思路：
1.解法一：可以使用哈希表，记录数字出现的个数，返回数字出现的次数恰好为一次的数字

2.解法二：使用比特位计数的思想，根据某一个比特位的值总和 % 3的结果，快速定位到该比特位的值是0还是1，然后通过每一个比特位上的值将数字进行还原

代码实现：

class Solution {
public:int singleNumber(vector<int>& nums) {int ret = 0;for(int i = 0;i < 32;i++){int sum = 0;for(int x : nums){if(((x >> i) & 1) == 1)sum++;}sum %= 3;if(sum == 1)ret |= 1 << i;}return ret;}
};

🎄五、消失的两个数字

题目链接：消失的两个数字

题目描述：

解题思路：
1.由题我们可知：假设数组大小为n，则数据范围在[1，n + 2]之间

2.将所有的数都异或在一起，得到两个数

3.找出两个数比特位不同的那一位进行区分

4.因此将数字划分为两类进行异或，最终得到结果

代码实现：

class Solution {
public:vector<int> missingTwo(vector<int>& nums) {int n = nums.size() + 2;int tmp = 0;for(auto x :nums){tmp ^= x;}for(int i = 1;i <= n;i++){tmp ^= i;}int diff = 0;//区分最后一位是1还是0while(1){if(((tmp >> diff) & 1) == 1)break;elsediff++;}int x1 = 0,x2 = 0;for(auto x : nums){if(((x >> diff) & 1) == 1){x1 ^= x;}else{x2 ^= x;}}for(int i = 1;i <= n;i++){if(((i >> diff) & 1) == 1){x1 ^= i;}else{x2 ^= i;}}return {x1,x2};}
};