当前位置：首页 > news >正文

【MATLAB例程】基于梯度检测自适应的互补滤波 vs 标准互补滤波，附MATLAB代码下载链接，可直接运行，方便学习和修改成自己想要的程序

news 2025/10/31 8:22:51

在这里插入图片描述

基于加速度梯度检测和平滑误差反馈的自适应互补滤波（Gradient-based Adaptive Complementary Filter, GACF），MATLAB例程，与滤波前、标准互补滤波进行对比

文章目录

程序简介
- 算法原理
- 程序功能模块
运行结果
MATLAB源代码

程序简介

程序实现：基于加速度梯度检测和平滑误差反馈的自适应互补滤波（Gradient-based Adaptive Complementary Filter, GACF），并与标准互补滤波器进行性能对比。
算法用于融合加速度计与陀螺仪数据，以估计目标角度，重点在于在存在外部加速度干扰和陀螺仪漂移的情况下，提升姿态估计的稳健性与动态响应性能。

算法原理

传统互补滤波采用固定权重系数 ( \alpha )：
$θest(t)=α[θest(t−Δt)+ωgΔt]+(1−α)θa\theta_{est}(t) = \alpha [\theta_{est}(t-\Delta t) + \omega_g \Delta t] + (1-\alpha)\theta_a$
其中陀螺仪积分部分响应快但易漂移，加速度计部分长期稳定但易受外加线加速度影响。固定权重无法同时兼顾两者特性。

改进的 GACF 引入信号梯度检测与误差反馈调节机制，动态调整滤波权重：
$αt=α0+k1∣Δθa∣+k2∣θa−θest∣\alpha_t = \alpha_0 + k_1|\Delta \theta_a| + k_2|\theta_a - \theta_{est}|$
$α(t)=α(t−1)+β[αt−α(t−1)]\alpha(t) = \alpha(t-1) + \beta [\alpha_t - \alpha(t-1)]$
其中：

$∣Δθa∣|\Delta \theta_a|$ ：加速度角度的变化率（检测外加加速度强度）；
$∣θa−θest∣|\theta_a - \theta_{est}|$ ：融合误差；
$k_1, k_2$ ：敏感系数；
$β\beta$ ：平滑更新速率。

当系统处于平稳状态时， $Δθa\Delta \theta_a$ 较小，算法自动降低陀螺权重以减小漂移；
当检测到剧烈运动或外加干扰时， $Δθa\Delta \theta_a$ 变大，算法会增大陀螺权重，增强动态跟踪能力。

程序功能模块

仿真信号生成
生成包含漂移、噪声及外部加速度干扰的陀螺仪与加速度计数据。
标准互补滤波实现
采用固定权重 α=0.98 的传统互补滤波，作为基准。
改进的梯度检测自适应滤波
实时检测加速度变化率并结合误差反馈，平滑更新 α，实现动态权重调整。
结果可视化与误差分析
输出角度估计曲线、误差曲线及 RMSE 对比，直观展示改进效果。

运行结果

各方法得到的角度曲线对比：
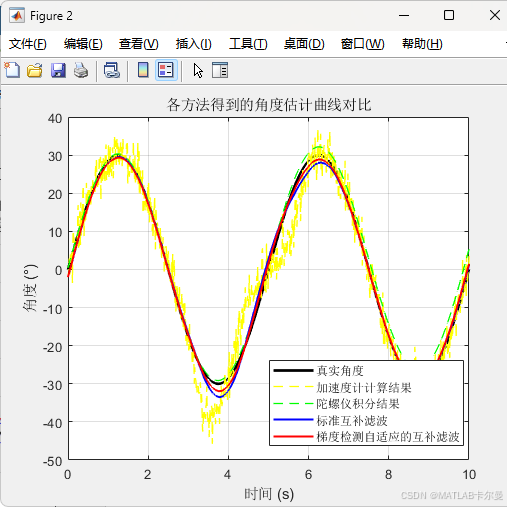
在这里插入图片描述

各方法得到的角度误差曲线对比：
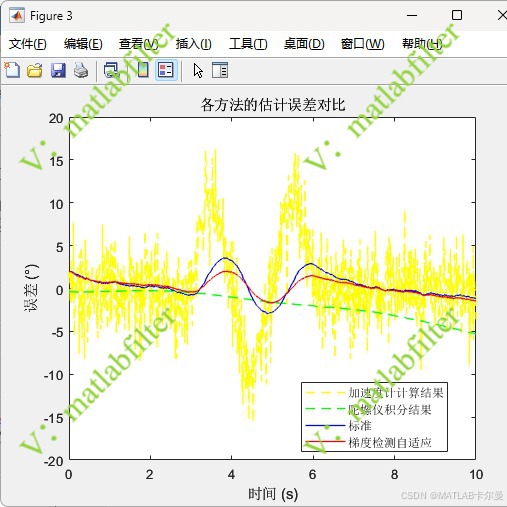
在这里插入图片描述

误差特性输出：
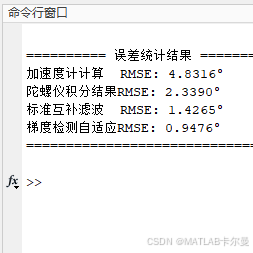
在这里插入图片描述

程序结构：
在这里插入图片描述

MATLAB源代码

完整代码如下：

%% 基于梯度检测自适应的互补滤波器方法与标准互补滤波对比
% 作者：matlabfilter
% 2025-10-26/Ver1clear; close all; clc;
rng(0);
%% 生成仿真数据
dt = 0.01; % 采样时间
t = 0:dt:10; % 时间向量
N = length(t);% 真实角度 (正弦运动)
true_angle = 30*sin(2*pi*0.2*t);
true_angular_vel = 30*2*pi*0.2*cos(2*pi*0.2*t);
...