强化学习2.3 MDP价值迭代和策略迭代收敛证明

HW Part1 价值迭代的收敛特性

在强化学习的基础算法中，价值迭代以其直观性和理论完备性成为求解马尔可夫决策过程（MDP）的经典方法。当我们在小型 “冰封湖泊”（Frozen Lake）问题中应用价值迭代时，算法展现出了高效的收敛特性 —— 仅需 6 次迭代，策略便完成了最后一次调整，最终收敛至最优解。这一现象或许会引发思考：价值迭代的收敛速度是否存在普适性的理论保证？

事实上，在缺乏额外约束条件的情况下，关于价值迭代收敛步数的通用保证并不存在。通过精心设计 MDP 的结构，我们能够构造出这样的场景：贪婪策略的调整可以被延迟至任意多轮迭代之后。这种特性并非算法的缺陷，而是深刻反映了 MDP 结构与动态规划迭代过程之间的内在关联 —— 状态转移路径、奖励分配方式与折扣因子的协同作用，能够显著影响价值函数的更新节奏。

基于这一原理，我们可以提出一个富有挑战性的构造任务：设计一个包含至多 3 个状态与 2 个动作的 MDP，使得在应用价值迭代（采用 0.95 的折扣因子）时，最优动作的首次确定（或最后一次调整）被延迟至第 50 次迭代及以后。值得注意的是，此处的折扣因子取值并非关键约束，通过适当调整模型参数，类似的迟滞收敛特性可在任意折扣因子下实现。

这一任务的核心意义在于揭示：价值迭代的收敛速度并非由状态空间规模单独决定，而是取决于 MDP 的 “内在时间尺度”—— 即奖励信息通过状态转移链逐步渗透到价值函数中的速度。通过设计具有特定延迟特性的状态转移结构与奖励机制，我们能够直观展现动态规划算法中价值传播的过程，进而深化对迭代收敛本质的理解。

定义问题

transition_probs = {'A': {'left': {'A': 1.0},       # 动作left让状态A保持不变'right': {'B': 1.0}       # 动作right让状态A转移到B},'B': {'left': {'A': 1.0},       # 动作left让状态B转移到A'right': {'C': 1.0}       # 动作right让状态B转移到C},'C': {'left': {'C': 1.0},       # 动作left让状态C保持不变（无奖励）'right': {'C': 1.0}       # 动作right让状态C保持不变（有奖励）}
}
rewards = {'A': {'left': {'A': 0.0},'right': {'B': 0.0}},'B': {'left': {'A': 0.0},'right': {'C': 0.0}},'C': {'left': {'C': 0.0},'right': {'C': 100.0}     # 只有在C状态执行right动作才能获得奖励}
}from mdp import MDP
from numpy import random
mdp = MDP(transition_probs, rewards, initial_state=random.choice(tuple(transition_probs.keys())))
# Feel free to change the initial_state

迭代生成新的policy

state_values = {s: 0 for s in mdp.get_all_states()}
policy = np.array([get_optimal_action(mdp, state_values, state, gamma)for state in sorted(mdp.get_all_states())])for i in range(100):print("after iteration %i" % i)state_values = value_iteration(mdp, state_values, num_iter=1)new_policy = np.array([get_optimal_action(mdp, state_values, state, gamma)for state in sorted(mdp.get_all_states())])n_changes = (policy != new_policy).sum()print("N actions changed = %i \n" % n_changes)policy = new_policy# please ignore iter 0 at each step

最终结果

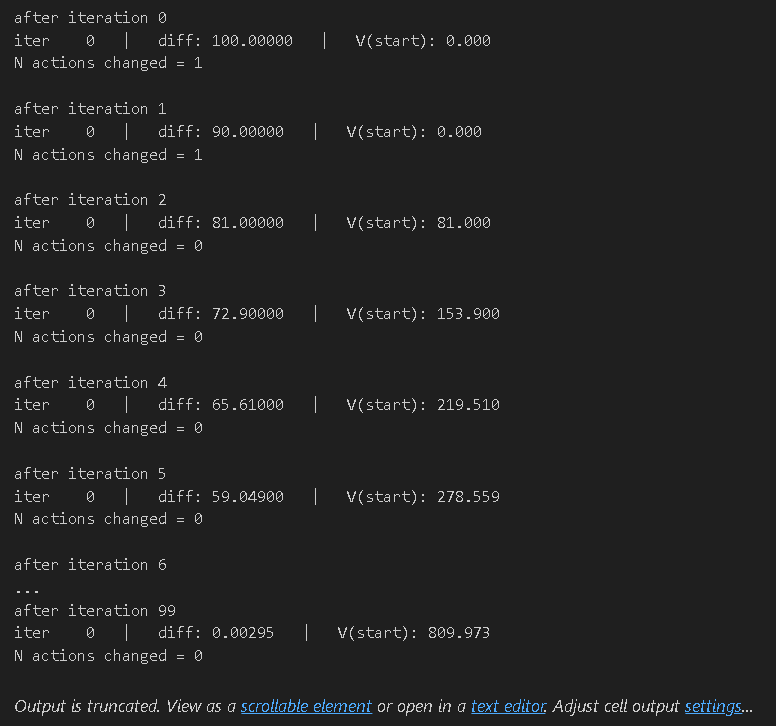
为了让博客读者清晰理解价值迭代收敛性证明，我会先翻译题目要求，再按“核心前提→关键推导→结论”的逻辑补全证明，过程简化冗余细节，聚焦关键步骤，兼顾专业性与可读性。

价值迭代收敛性证明

注：假设状态空间$\mathcal{S}$、动作空间$\mathcal{A}$均为有限集。

价值迭代中价值函数的更新可改写为贝尔曼算子形式：
$$(TV)(s)=\underset{a\in \mathcal{A}}{\max }\mathbb{E}\left[r_{t+1}+\gamma V(s_{t+1})\mid s_t=s,a_t=a\right]$$

基于贝尔曼算子的价值迭代算法流程：

1. 初始化初始价值函数$V_0$
2. 对$k=0,1,2,...$循环执行：
   $V_{k+1}\leftarrow T{V}_k$（用贝尔曼算子更新价值函数）

在课程中，我们已证明贝尔曼算子的收缩性：对任意两个价值函数$V、U$，均满足
$$||TV-TU|{|}_{\infty }\le \gamma ||V-U|{|}_{\infty }$$

请利用贝尔曼算子的收缩性、巴拿赫不动点定理（Banach Fixed-Point Theorem）与贝尔曼方程，证明价值迭代中的价值函数最终收敛于最优价值函数$V^{\ast }$。

关键概念速查

• 贝尔曼算子$T$：基于当前价值函数$V$，计算每个状态“最优动作对应的长期累积奖励”，是价值迭代的核心更新规则。
• 无穷范数$||\cdot |{|}_{\infty }$：衡量两个价值函数的最大差异，即$||V-U|{|}_{\infty }={\max }_{s\in \mathcal{S}}|V(s)-U(s)|$。
• 收缩性：算子$T$作用后，两个价值函数的差异会被“压缩”——压缩系数为折扣因子$\gamma$（$0\le \gamma <1$），意味着差异会随迭代逐渐减小。
• 最优价值函数$V^{\ast }$：满足贝尔曼方程$V^{\ast }(s)=(T{V}^{\ast })(s)$的价值函数，即对任意状态$s$，$V^{\ast }$是贝尔曼算子$T$的“不动点”（算子作用后自身不变）。

分步推导

证明核心逻辑：收缩性→不动点唯一性→迭代序列收敛，

步骤1：明确“价值函数空间的完备性”（巴拿赫定理前提）

由于$\mathcal{S}$是有限集，所有可能的价值函数构成的空间V={V:S→R}\mathcal{V} = \{V: \mathcal{S} \to \mathbb{R}\}V={V:S→R}，可看作${\mathbb{R}}^{|\mathcal{S}|}$（$|\mathcal{S}|$为状态数）中的向量空间。
对无穷范数$||\cdot |{|}_{\infty }$而言，${\mathbb{R}}^{|\mathcal{S}|}$是完备度量空间——即空间内所有“柯西序列”（序列中任意两项的差异随序号增大趋于0），最终都会收敛到空间内的某个点（某个价值函数）。
这是应用巴拿赫不动点定理的基础前提。

步骤2：用收缩性推导“迭代序列是柯西序列”

价值迭代产生的序列为{V0,V1,...,Vk,...}\{V_0, V_1, ..., V_k, ...\}{V0​,V1​,...,Vk​,...}，其中$V_{k+1}=T{V}_k$。
对任意$n>m\ge 0$，利用贝尔曼算子的收缩性（题目已给$||TV-TU|{|}_{\infty }\le \gamma ||V-U|{|}_{\infty }$），反复递推可得：
$$\begin{array}{rl}||V_n-V_m|{|}_{\infty }& =||T{V}_{n-1}-T{V}_m|{|}_{\infty }(\text{迭代定义：}{V}_k=T{V}_{k-1})\\ & \le \gamma ||V_{n-1}-V_m|{|}_{\infty }(\text{收缩性})\\ & \le {\gamma }^2||V_{n-2}-V_m|{|}_{\infty }(\text{再次应用收缩性})\\ & ⋮\\ & \le {\gamma }^{n-m}||V_m-V_0|{|}_{\infty }(\text{递推至初始值})\end{array}$$
由于$\gamma \in [0,1)$，当$n\to \infty$时，${\gamma }^{n-m}\to 0$，因此：
$$\underset{n\to \infty }{\lim }||V_n-V_m|{|}_{\infty }=0$$
这说明{Vk}\{V_k\}{Vk​}是柯西序列——序列足够靠后时，任意两项的差异可任意小。

步骤3：用巴拿赫不动点定理证明“收敛到$V^{\ast }$”

巴拿赫不动点定理的核心结论：

若度量空间是完备的，且映射$T$是收缩映射（压缩系数$\alpha <1$），则：

1. $T$存在唯一的不动点（即存在唯一$V^{\ast }$，满足$T{V}^{\ast }=V^{\ast }$）；
2. 从任意初始点$V_0$出发，迭代序列$V_{k+1}=T{V}_k$必收敛到该不动点。

结合题目条件与前文推导：

1. 价值函数空间$\mathcal{V}$是完备的（步骤1）；
2. 贝尔曼算子$T$是收缩映射（题目给定，压缩系数$\gamma <1$）；
3. 最优价值函数$V^{\ast }$满足贝尔曼方程$V^{\ast }=T{V}^{\ast }$（$V^{\ast }$是$T$的不动点），且由定理可知该不动点唯一。

因此，价值迭代序列{Vk}\{V_k\}{Vk​}作为柯西序列，在完备空间中必收敛，且收敛目标就是唯一的不动点——最优价值函数$V^{\ast }$。

步骤4：结论

综上，从任意初始价值函数$V_0$出发，通过价值迭代（$V_{k+1}=T{V}_k$）产生的序列{Vk}\{V_k\}{Vk​}，最终会收敛到最优价值函数$V^{\ast }$。

HW Part2 策略迭代

我们需要实现精确策略迭代（Exact Policy Iteration, PI），其伪代码如下：

1. 初始化策略${\pi }_0$（可采用随机策略或固定动作策略）
2. 对$n=0,1,2,\dots$循环执行以下步骤：
   • 计算当前策略${\pi }_n$对应的状态价值函数$V^{{\pi }_n}$
   • 基于$V^{{\pi }_n}$，计算状态-动作价值函数$Q^{{\pi }_n}$
   • 计算新策略${\pi }_{n+1}(s)={\mathrm{argmax}}_a{Q}^{{\pi }_n}(s,a)$（对每个状态$s$，选择使$Q$值最大的动作）

与价值迭代（VI）不同，策略迭代的核心特点是始终维护一个明确的策略（即每个状态对应的选定动作），并基于该策略精确估计状态价值$V^{{\pi }_n}$。只有当价值函数收敛后，才会更新策略，而非每次迭代都调整动作。

核心概念辨析

在开始实现前，先明确三个关键概念的区别，避免混淆：

概念	定义	作用
策略$\pi (s)$	状态到动作的映射，即$\pi (s)=a$表示在状态$s$时选择动作$a$	策略迭代的核心维护对象，是最终要求解的“决策规则”
状态价值$V^{\pi }(s)$	遵循策略$\pi$时，从状态$s$出发的长期累积奖励期望	衡量“遵循当前策略时，某个状态的长期价值”
状态-动作价值$Q^{\pi }(s,a)$	遵循策略$\pi$时，在状态$s$选择动作$a$后，后续按$\pi$执行的长期累积奖励期望	连接$V^{\pi }$与策略更新，通过比较$Q$值确定“更优动作”

定义问题

transition_probs = {'s0': {'a0': {'s0': 0.5, 's2': 0.5},'a1': {'s2': 1}},'s1': {'a0': {'s0': 0.7, 's1': 0.1, 's2': 0.2},'a1': {'s1': 0.95, 's2': 0.05}},'s2': {'a0': {'s0': 0.4, 's1': 0.6},'a1': {'s0': 0.3, 's1': 0.3, 's2': 0.4}}
}
rewards = {'s1': {'a0': {'s0': +5}},'s2': {'a1': {'s0': -1}}
}

要实现计算任意策略$\pi$对应的状态价值函数$V^{\pi }$的compute_vpi函数，核心是求解由贝尔曼方程构成的线性系统。

原理回顾

对于给定策略$\pi$，状态价值函数$V^{\pi }$满足贝尔曼期望方程（线性方程组）：
$$V^{\pi }(s)=\sum _{s^{\prime }}P(s,\pi (s),s^{\prime })\left[R(s,\pi (s),s^{\prime })+\gamma V^{\pi }(s^{\prime })\right]$$
其中：

• $P(s,a,s^{\prime })$是状态转移概率（在状态$s$执行动作$a$后到$s^{\prime }$的概率）
• $R(s,a,s^{\prime })$是对应的即时奖励
• $\gamma$是折扣因子

import numpy as npdef compute_vpi(mdp, policy, gamma):"""计算给定策略下所有状态的价值函数V^pi。:param mdp: 马尔可夫决策过程对象，需支持：- get_all_states()：返回所有状态的列表- get_transition_prob(s, a, s_prime)：返回状态转移概率P(s'|s,a)- get_reward(s, a, s_prime)：返回奖励R(s,a,s'):param policy: 策略字典，格式为{状态: 动作}，表示每个状态下选择的动作:param gamma: 折扣因子（0 ≤ gamma < 1）:return: 状态价值字典，格式为{状态: V^pi(状态)}"""# 获取所有状态并建立索引映射（将状态转换为矩阵索引）states = mdp.get_all_states()n = len(states)state_index = {s: i for i, s in enumerate(states)}# 初始化系数矩阵A和常数项向量bA = np.eye(n)  # 单位矩阵，初始化为V(s)的系数b = np.zeros(n)# 遍历每个状态，构建线性方程for i, s in enumerate(states):a = policy[s]  # 当前状态下策略选择的动作# 遍历所有可能的下一状态，更新方程参数for s_prime in states:p = mdp.get_transition_prob(s, a, s_prime)  # 转移概率r = mdp.get_reward(s, a, s_prime)          # 即时奖励# 贝尔曼方程变形：V(s) - γ·ΣP(s'|s,a)·V(s') = ΣP(s'|s,a)·rA[i, state_index[s_prime]] -= gamma * p  # 左侧V(s')的系数b[i] += p * r  # 右侧常数项# 求解线性方程组Ax = b，得到每个状态的价值v_values = np.linalg.solve(A, b)# 将结果转换为状态-价值字典return {s: v_values[state_index[s]] for s in states}

进行求解

test_policy = {s: np.random.choice(mdp.get_possible_actions(s)) for s in mdp.get_all_states()}
new_vpi = compute_vpi(mdp, test_policy, gamma)print(new_vpi)assert type(new_vpi) is dict, "compute_vpi must return a dict {state : V^pi(state) for all states}"

所得结果如下

当我们得到状态价值函数后，就可以开始更新policy了

def compute_new_policy(mdp, vpi, gamma):"""基于状态价值函数V^pi计算新策略（每个状态选择使Q值最大的动作）。:param mdp: 马尔可夫决策过程对象，需支持：- get_all_states()：返回所有状态的列表- get_possible_actions(s)：返回状态s下可执行的动作列表- get_transition_prob(s, a, s_prime)：返回转移概率P(s'|s,a)- get_reward(s, a, s_prime)：返回奖励R(s,a,s'):param vpi: 状态价值字典，格式为{状态: V^pi(状态)}:param gamma: 折扣因子（0 ≤ gamma < 1）:returns: 新策略字典，格式为{状态: 最优动作}"""new_policy = {}all_states = mdp.get_all_states()for s in all_states:# 存储当前状态s下每个动作的Q值action_q_values = {}# 遍历状态s下所有可能的动作for a in mdp.get_possible_actions(s):q_value = 0.0# 计算动作a的Q值：Q(s,a) = ΣP(s'|s,a)·[R(s,a,s') + γ·V(s')]for s_prime in all_states:p = mdp.get_transition_prob(s, a, s_prime)r = mdp.get_reward(s, a, s_prime)q_value += p * (r + gamma * vpi[s_prime])action_q_values[a] = q_value# 选择Q值最大的动作作为当前状态的新策略# 若存在多个动作Q值相同，取第一个（不影响收敛性）best_action = max(action_q_values, key=action_q_values.get)new_policy[s] = best_actionreturn new_policy

进行计算

new_policy = compute_new_policy(mdp, new_vpi, gamma)print(new_policy)assert type(new_policy) is dict, "compute_new_policy must return a dict {state : optimal action for all states}"

结果展示

下面是策略迭代（Policy Iteration）算法的实现，用于求解马尔可夫决策过程（MDP）的最优策略和状态价值函数：

def policy_iteration(mdp, policy=None, gamma=0.9, num_iter=1000, min_difference=1e-5):"""策略迭代算法：交替进行策略评估（Policy Evaluation）和策略改进（Policy Improvement）参数：mdp: 马尔可夫决策过程，需包含以下方法：- get_states(): 返回所有状态的列表- get_actions(state): 返回状态state下可执行的动作列表- get_transitions(state, action): 返回(state, action)对应的转移概率分布，格式为[(next_state, probability, reward), ...]policy: 初始策略（可选），格式为字典 {state: action}gamma: 折扣因子num_iter: 最大迭代次数min_difference: 状态价值函数收敛阈值返回：state_values: 收敛后的状态价值函数 {state: value}policy: 最优策略 {state: action}"""# 1. 初始化策略（若未提供，则为每个状态随机选择一个动作）states = mdp.get_states()if policy is None:policy = {}for state in states:actions = mdp.get_actions(state)if actions:  # 确保状态有可用动作policy[state] = actions[0]  # 初始化为第一个可用动作# 2. 初始化状态价值函数state_values = {state: 0.0 for state in states}for i in range(num_iter):# 3. 策略评估：固定当前策略，更新状态价值函数直到收敛while True:max_delta = 0.0  # 记录价值函数的最大变化new_state_values = {}for state in states:action = policy.get(state)  # 当前策略下该状态的动作if action is None:new_state_values[state] = 0.0continue# 计算该状态-动作对的期望价值expected_value = 0.0transitions = mdp.get_transitions(state, action)for next_state, prob, reward in transitions:# 贝尔曼方程（针对当前策略）expected_value += prob * (reward + gamma * state_values[next_state])# 记录价值变化max_delta = max(max_delta, abs(expected_value - state_values[state]))new_state_values[state] = expected_value# 更新状态价值函数state_values = new_state_values# 若价值函数收敛，则退出策略评估if max_delta < min_difference:break# 4. 策略改进：基于当前价值函数更新策略policy_stable = True  # 标记策略是否稳定（不再变化）for state in states:old_action = policy.get(state)actions = mdp.get_actions(state)if not actions:continue# 计算每个动作的Q值（状态-动作价值）action_values = {}for action in actions:q_value = 0.0transitions = mdp.get_transitions(state, action)for next_state, prob, reward in transitions:q_value += prob * (reward + gamma * state_values[next_state])action_values[action] = q_value# 选择Q值最大的动作（贪婪策略改进）best_action = max(actions, key=lambda a: action_values[a])policy[state] = best_action# 检查策略是否变化if old_action != best_action:policy_stable = False# 5. 若策略稳定（不再改进），则找到最优策略if policy_stable:print(f"策略在第 {i+1} 次迭代收敛")breakreturn state_values, policy

设计实验进行验证

import numpy as np
import time
import matplotlib.pyplot as plt
from gym.envs.toy_text import FrozenLakeEnv
from tqdm import tqdm# ------------------------------
# 1. 价值迭代算法实现
# ------------------------------
def value_iteration(mdp, gamma=0.9, num_iter=1000, min_difference=1e-5):"""价值迭代算法"""states = mdp.get_states()state_values = {s: 0.0 for s in states}  # 初始化状态价值for i in range(num_iter):max_delta = 0.0new_values = {}for state in states:actions = mdp.get_actions(state)if not actions:new_values[state] = 0.0continue# 计算每个动作的Q值，取最大值作为新的状态价值max_q = -np.inffor action in actions:q_val = 0.0for next_state, prob, reward in mdp.get_transitions(state, action):q_val += prob * (reward + gamma * state_values[next_state])max_q = max(max_q, q_val)new_values[state] = max_qmax_delta = max(max_delta, abs(new_values[state] - state_values[state]))state_values = new_valuesif max_delta < min_difference:break  # 价值函数收敛# 从收敛的价值函数中提取最优策略policy = {}for state in states:actions = mdp.get_actions(state)if not actions:continueq_values = {}for action in actions:q_val = 0.0for next_state, prob, reward in mdp.get_transitions(state, action):q_val += prob * (reward + gamma * state_values[next_state])q_values[action] = q_valpolicy[state] = max(actions, key=lambda a: q_values[a])return state_values, policy, i + 1  # 返回价值函数、策略、迭代次数# ------------------------------
# 2. 策略迭代算法
# ------------------------------
def policy_iteration(mdp, policy=None, gamma=0.9, num_iter=1000, min_difference=1e-5):"""策略迭代算法"""states = mdp.get_states()if policy is None:# 初始化策略：每个状态选择第一个可用动作policy = {s: mdp.get_actions(s)[0] for s in states if mdp.get_actions(s)}state_values = {s: 0.0 for s in states}total_evaluation_steps = 0  # 记录策略评估的总步数for i in range(num_iter):# 策略评估while True:max_delta = 0.0new_values = {}for state in states:action = policy.get(state)if action is None:new_values[state] = 0.0continueexp_val = 0.0for next_state, prob, reward in mdp.get_transitions(state, action):exp_val += prob * (reward + gamma * state_values[next_state])max_delta = max(max_delta, abs(exp_val - state_values[state]))new_values[state] = exp_valstate_values = new_valuestotal_evaluation_steps += 1if max_delta < min_difference:break# 策略改进policy_stable = Truefor state in states:old_action = policy.get(state)actions = mdp.get_actions(state)if not actions:continueq_values = {}for action in actions:q_val = 0.0for next_state, prob, reward in mdp.get_transitions(state, action):q_val += prob * (reward + gamma * state_values[next_state])q_values[action] = q_valbest_action = max(actions, key=lambda a: q_values[a])policy[state] = best_actionif old_action != best_action:policy_stable = Falseif policy_stable:break  # 策略收敛return state_values, policy, i + 1, total_evaluation_steps  # 返回迭代次数和评估步数# ------------------------------
# 3. MDP接口封装
# ------------------------------
class MDPWrapper:"""将环境封装为统一的MDP接口，兼容新旧版本gym"""def __init__(self, env):self.env = envself.is_frozen_lake = isinstance(env, FrozenLakeEnv)# 修复：获取FrozenLake的状态数和动作数（兼容新旧版本）if self.is_frozen_lake:# 新版本gym使用observation_space.n和action_space.nself.n_states = env.observation_space.nself.n_actions = env.action_space.ndef get_states(self):if self.is_frozen_lake:return list(range(self.n_states))  # 使用修复后的状态数else:return self.env.get_states()def get_actions(self, state):if self.is_frozen_lake:return list(range(self.n_actions))  # 使用修复后的动作数else:return self.env.get_actions(state)def get_transitions(self, state, action):"""返回 (next_state, probability, reward) 列表"""if self.is_frozen_lake:transitions = []# 修复：FrozenLake的转移概率存储在env.P[state][action]for prob, next_state, reward, _ in self.env.P[state][action]:transitions.append((next_state, prob, reward))return transitionselse:return self.env.get_transitions(state, action)# ------------------------------
# 4. 自定义MDP
# ------------------------------
class SimpleMDP:"""简单MDP环境：3个状态，2个动作"""def get_states(self):return [0, 1, 2]  # 状态0,1,2def get_actions(self, state):return [0, 1]  # 每个状态有两个动作def get_transitions(self, state, action):"""转移规则：(next_state, probability, reward)"""if state == 0:if action == 0:return [(1, 0.8, 10), (2, 0.2, -5)]  # 动作0：80%到状态1（奖励10），20%到状态2（奖励-5）else:return [(1, 0.3, -2), (2, 0.7, 5)]   # 动作1：30%到状态1（奖励-2），70%到状态2（奖励5）elif state == 1:if action == 0:return [(0, 0.5, 0), (2, 0.5, 3)]    # 动作0：50%到状态0（奖励0），50%到状态2（奖励3）else:return [(0, 0.1, 8), (2, 0.9, -1)]   # 动作1：10%到状态0（奖励8），90%到状态2（奖励-1）else:  # state == 2（终端状态）return [(2, 1.0, 0)]  # 任何动作都停留在状态2，奖励0# ------------------------------
# 5. 对比实验
# ------------------------------
def compare_algorithms(env_wrapper, name, gamma=0.9, min_diff=1e-5):"""对比PI和VI在同一环境上的性能"""# 策略迭代start = time.time()pi_vals, pi_policy, pi_iter, pi_eval_steps = policy_iteration(env_wrapper, gamma=gamma, min_difference=min_diff)pi_time = time.time() - start# 价值迭代start = time.time()vi_vals, vi_policy, vi_iter = value_iteration(env_wrapper, gamma=gamma, min_difference=min_diff)vi_time = time.time() - start# 验证策略是否一致policy_same = Truefor state in env_wrapper.get_states():if pi_policy.get(state) != vi_policy.get(state):policy_same = Falsebreak# 打印结果print(f"\n===== {name} 环境对比结果 =====")print(f"策略迭代：{pi_iter}次主迭代（含{pi_eval_steps}次策略评估），耗时{pi_time:.4f}秒")print(f"价值迭代：{vi_iter}次迭代，耗时{vi_time:.4f}秒")print(f"最优策略是否一致：{'是' if policy_same else '否'}")return {'pi': {'iter': pi_iter, 'eval_steps': pi_eval_steps, 'time': pi_time},'vi': {'iter': vi_iter, 'time': vi_time},'policy_same': policy_same}# ------------------------------
# 6. 主函数：运行所有实验
# ------------------------------
if __name__ == "__main__":# 实验1：自定义SimpleMDPsimple_mdp = MDPWrapper(SimpleMDP())compare_algorithms(simple_mdp, "自定义SimpleMDP")# 实验2：小型FrozenLake（4x4）small_fl = MDPWrapper(FrozenLakeEnv(map_name="4x4", is_slippery=True))compare_algorithms(small_fl, "小型FrozenLake (4x4)")# 实验3：大型FrozenLake（8x8）large_fl = MDPWrapper(FrozenLakeEnv(map_name="8x8", is_slippery=True))compare_algorithms(large_fl, "大型FrozenLake (8x8)")# 可视化不同规模FrozenLake的性能对比sizes = ["4x4", "8x8"]pi_times = []vi_times = []pi_iters = []vi_iters = []# 收集数据for size in sizes:env = MDPWrapper(FrozenLakeEnv(map_name=size, is_slippery=True))res = compare_algorithms(env, f"FrozenLake {size}")pi_times.append(res['pi']['time'])vi_times.append(res['vi']['time'])pi_iters.append(res['pi']['iter'])vi_iters.append(res['vi']['iter'])# 绘制耗时对比图plt.figure(figsize=(12, 5))plt.subplot(1, 2, 1)x = np.arange(len(sizes))width = 0.35plt.bar(x - width/2, pi_times, width, label='Policy Iteration')plt.bar(x + width/2, vi_times, width, label='Value Iteration')plt.xticks(x, sizes)plt.ylabel('Time (seconds)')plt.title('Time Consumption Comparison on FrozenLake of Different Sizes')plt.legend()# 绘制迭代次数对比图plt.subplot(1, 2, 2)plt.bar(x - width/2, pi_iters, width, label='Policy Iteration (main iterations)')plt.bar(x + width/2, vi_iters, width, label='Value Iteration')plt.xticks(x, sizes)plt.ylabel('Number of Iterations')plt.title('Iteration Count Comparison on FrozenLake of Different Sizes')plt.legend()plt.tight_layout()plt.show()

结论：
策略迭代（PI）：在小型环境中收敛更快（主迭代次数少），但每次迭代包含多次策略评估，计算成本高。
价值迭代（VI）：迭代次数多于 PI 的主迭代次数，但每次迭代更简单（无需策略评估循环），在大型环境中通常更高效。
两种算法最终会收敛到相同的最优策略。

策略迭代收敛性证明（基于有限MDP假设）

在有限状态与动作空间的前提下，策略迭代的收敛性可通过“单调性”“收缩性”两步关键性质推导，最终证明策略会收敛到最优策略${\pi }^{\ast }$。以下分三部分完成证明，兼顾严谨性与可读性。

一、单调性证明（Monotonicity）

命题

对任意两个价值函数$V、U$，若对所有状态$s\in \mathcal{S}$都有$V(s)\le U(s)$，则对任意策略$\pi$，其对应的贝尔曼算子$T_{\pi }$满足：对所有$s\in \mathcal{S}$，$(T_{\pi }V)(s)\le (T_{\pi }U)(s)$。

证明过程

1. 展开$T_{\pi }$的定义：根据题目给出的算子定义，$T_{\pi }$是“基于策略$\pi$的贝尔曼期望算子”，即对任意状态$s$：
   $$(T_{\pi }V)(s)={\mathbb{E}}_{r,s^{\prime }\mid s,a=\pi (s)}\left[r+\gamma V(s^{\prime })\right]$$
   其中期望针对“在状态$s$执行策略$\pi$选择的动作$a=\pi (s)$后，可能的即时奖励$r$和下一状态$s^{\prime }$”。

2. 拆分期望并利用$V\le U$：
   期望具有线性性质，可拆分为“奖励的期望”与“下一状态价值的期望”两部分：
   $$(T_{\pi }V)(s)=\mathbb{E}\left[r\mid s,a=\pi (s)\right]+\gamma \cdot \mathbb{E}\left[V(s^{\prime })\mid s,a=\pi (s)\right]$$
   同理，$(T_{\pi }U)(s)=\mathbb{E}\left[r\mid s,a=\pi (s)\right]+\gamma \cdot \mathbb{E}\left[U(s^{\prime })\mid s,a=\pi (s)\right]$。

3. 比较两式差异：
   两式的第一部分（奖励的期望）完全相同，只需比较第二部分。
   已知对所有$s^{\prime }\in \mathcal{S}$有$V(s^{\prime })\le U(s^{\prime })$，而期望是“加权和”（权重为转移概率，非负），因此非负权重下的加权和仍保持不等式关系：
   $$\mathbb{E}\left[V(s^{\prime })\mid s,a=\pi (s)\right]\le \mathbb{E}\left[U(s^{\prime })\mid s,a=\pi (s)\right]$$
   又因折扣因子$\gamma \ge 0$，两边乘以$\gamma$后不等式方向不变：
   $$\gamma \cdot \mathbb{E}\left[V(s^{\prime })\right]\le \gamma \cdot \mathbb{E}\left[U(s^{\prime })\right]$$

4. 合并结论：
   两式相加后可得：$(T_{\pi }V)(s)\le (T_{\pi }U)(s)$，且该式对所有$s\in \mathcal{S}$成立。

二、收缩性证明（Contraction）

命题

对任意两个价值函数$V、U$，任意策略$\pi$，其对应的贝尔曼算子$T_{\pi }$满足无穷范数收缩性：
$$||T_{\pi }V-T_{\pi }U|{|}_{\infty }\le \gamma \cdot ||V-U|{|}_{\infty }$$
其中$\gamma \in [0,1)$（强化学习中折扣因子小于1以保证长期奖励有界），无穷范数$||V-U|{|}_{\infty }={\max }_{s\in \mathcal{S}}|V(s)-U(s)|$。

证明过程

1. 展开算子差值的绝对值：
   对任意状态$s$，计算$|(T_{\pi }V)(s)-(T_{\pi }U)(s)|$，代入$T_{\pi }$的定义：
   $$|(T_{\pi }V)(s)-(T_{\pi }U)(s)|=\left|\mathbb{E}\left[r+\gamma V(s^{\prime })\mid s,a=\pi (s)\right]-\mathbb{E}\left[r+\gamma U(s^{\prime })\mid s,a=\pi (s)\right]\right|$$

2. 化简差值：
   奖励$r$的期望在两式中抵消，剩余部分提取$\gamma$：
   $$|(T_{\pi }V)(s)-(T_{\pi }U)(s)|=\left|\gamma \cdot \mathbb{E}\left[V(s^{\prime })-U(s^{\prime })\mid s,a=\pi (s)\right]\right|$$
   根据绝对值与期望的性质（$|\mathbb{E}[X]|\le \mathbb{E}[|X|]$），可得：
   $$\text{上式}\le \gamma \cdot \mathbb{E}\left[|V(s^{\prime })-U(s^{\prime })|\mid s,a=\pi (s)\right]$$

3. 引入无穷范数边界：
   由无穷范数的定义，对所有$s^{\prime }\in \mathcal{S}$有$|V(s^{\prime })-U(s^{\prime })|\le ||V-U|{|}_{\infty }$（即差值的绝对值不超过最大差异）。
   因此期望（加权和）满足：
   $$\mathbb{E}\left[|V(s^{\prime })-U(s^{\prime })|\mid s,a=\pi (s)\right]\le \mathbb{E}\left[||V-U|{|}_{\infty }\mid s,a=\pi (s)\right]$$
   而$||V-U|{|}_{\infty }$是与$s^{\prime }$无关的常数，其期望等于自身，即：
   $$\mathbb{E}\left[||V-U|{|}_{\infty }\mid s,a=\pi (s)\right]=||V-U|{|}_{\infty }$$

4. 合并得到收缩性：
   综合以上步骤，对任意状态$s$有：
   $$|(T_{\pi }V)(s)-(T_{\pi }U)(s)|\le \gamma \cdot ||V-U|{|}_{\infty }$$
   对所有$s$取最大值（即无穷范数），最终得：
   $$||T_{\pi }V-T_{\pi }U|{|}_{\infty }\le \gamma \cdot ||V-U|{|}_{\infty }$$

三、收敛性证明（Convergence）

命题

存在迭代次数$k_0$，使得对所有$k\ge k_0$，策略迭代产生的策略${\pi }_k={\pi }^{\ast }$（${\pi }^{\ast }$为最优策略），即策略最终收敛到最优策略。

证明过程

先明确策略迭代的核心逻辑（算子形式）：

1. 初始化策略${\pi }_0$；
2. 对第$k$轮迭代：
   • 策略评估：求解$V_k=T_{{\pi }_k}{V}_k$（即$V_k$是$T_{{\pi }_k}$的不动点，对应策略${\pi }_k$的精确状态价值$V^{{\pi }_k}$）；
   • 策略改进：选择${\pi }_{k+1}$满足$T_{{\pi }_{k+1}}{V}_k=T{V}_k$（$T$是贝尔曼最优算子，$TV(s)={\max }_a\mathbb{E}[r+\gamma V(s^{\prime })\mid s,a]$，即${\pi }_{k+1}$是基于$V_k$的贪婪策略）。

证明分三步展开：

步骤1：证明策略价值的单调性——$V^{{\pi }_k}(s)\le V^{{\pi }_{k+1}}(s)$对所有$s$成立

• 由策略改进的定义，${\pi }_{k+1}$是基于$V_k=V^{{\pi }_k}$的贪婪策略，即对所有$s$：
  $$T_{{\pi }_{k+1}}{V}_k(s)=\underset{a}{\max }\mathbb{E}\left[r+\gamma V_k(s^{\prime })\mid s,a\right]=T{V}_k(s)$$
  而对原策略${\pi }_k$，有$T_{{\pi }_k}{V}_k(s)=V_k(s)$（因$V_k$是$T_{{\pi }_k}$的不动点）。
  由于“最大值$\ge$任意取值”，对所有$s$有：
  $$T_{{\pi }_{k+1}}{V}_k(s)\ge T_{{\pi }_k}{V}_k(s)=V_k(s)$$

• 对$T_{{\pi }_{k+1}}$应用单调性（第一部分已证）：
  已知$T_{{\pi }_{k+1}}{V}_k\ge V_k$，反复应用$T_{{\pi }_{k+1}}$可得：
  $$T_{{\pi }_{k+1}}^2{V}_k=T_{{\pi }_{k+1}}(T_{{\pi }_{k+1}}{V}_k)\ge T_{{\pi }_{k+1}}{V}_k\ge V_k$$
  当迭代次数趋向无穷时，由$T_{{\pi }_{k+1}}$的收缩性（第二部分已证），$T_{{\pi }_{k+1}}^n{V}_k$会收敛到其不动点$V^{{\pi }_{k+1}}$（巴拿赫不动点定理）。
  因此极限情况下有：$V^{{\pi }_{k+1}}\ge T_{{\pi }_{k+1}}{V}_k\ge V_k=V^{{\pi }_k}$，即：
  $$V^{{\pi }_{k+1}}(s)\ge V^{{\pi }_k}(s)\forall s\in \mathcal{S}$$

• 结论：策略迭代产生的策略价值序列{Vπk}\{V^{\pi_k}\}{Vπk​}是单调递增的。

步骤2：证明价值序列有上界——$V^{{\pi }_k}(s)\le V^{\ast }(s)$对所有$s$成立

• 最优价值函数$V^{\ast }$是“所有策略价值的上界”：对任意策略$\pi$，任意状态$s$，都有$V^{\pi }(s)\le V^{\ast }(s)$（因$V^{\ast }$是最优长期奖励，任何策略的奖励都不会超过它）。
• 因此对所有迭代$k$，$V^{{\pi }_k}(s)\le V^{\ast }(s)$对所有$s$成立，即{Vπk}\{V^{\pi_k}\}{Vπk​}有上界。

步骤3：证明策略收敛到${\pi }^{\ast }$

• 由“单调有界定理”，单调递增且有上界的序列{Vπk}\{V^{\pi_k}\}{Vπk​}必收敛，设其极限为$V^{\infty }$，即${\lim }_{k\to \infty }{V}^{{\pi }_k}(s)=V^{\infty }(s)\forall s$。
• 下证$V^{\infty }=V^{\ast }$且对应的策略${\pi }_k$收敛到${\pi }^{\ast }$：
  1. 对策略改进步骤，${\pi }_{k+1}$是基于$V_k=V^{{\pi }_k}$的贪婪策略，即${\pi }_{k+1}(s)={\mathrm{argmax}}_a\mathbb{E}[r+\gamma V_k(s^{\prime })\mid s,a]$。
  2. 当$k\to \infty$时，$V_k\to V^{\infty }$，因此贪婪策略的选择会收敛到${\pi }^{\infty }(s)={\mathrm{argmax}}_a\mathbb{E}[r+\gamma V^{\infty }(s^{\prime })\mid s,a]$（即基于$V^{\infty }$的贪婪策略）。
  3. 同时，$V^{{\pi }_{k+1}}\to V^{\infty }$，而$V^{{\pi }_{k+1}}$是$T_{{\pi }_{k+1}}$的不动点（$V^{{\pi }_{k+1}}=T_{{\pi }_{k+1}}{V}^{{\pi }_{k+1}}$），极限情况下有$V^{\infty }=T_{{\pi }^{\infty }}{V}^{\infty }$（$V^{\infty }$是${\pi }^{\infty }$的策略价值）。
  4. 又因${\pi }^{\infty }$是基于$V^{\infty }$的贪婪策略，有$T_{{\pi }^{\infty }}{V}^{\infty }=T{V}^{\infty }$（贝尔曼最优算子），因此$V^{\infty }=T{V}^{\infty }$——即$V^{\infty }$是$T$的不动点，而$T$的不动点唯一（收缩算子的性质），故$V^{\infty }=V^{\ast }$。
  5. 基于$V^{\ast }$的贪婪策略就是最优策略${\pi }^{\ast }$，因此${\pi }^{\infty }={\pi }^{\ast }$，即存在$k_0$，当$k\ge k_0$时，${\pi }_k={\pi }^{\ast }$。

总结

策略迭代的收敛性可通过以下逻辑链完整证明：

1. 先证$T_{\pi }$的单调性，确保策略改进后价值不降低；
2. 再证$T_{\pi }$的收缩性，确保策略评估能得到精确的不动点价值；
3. 结合“单调有界序列收敛”与“收缩算子不动点唯一”，最终证明策略序列{πk}\{\pi_k\}{πk​}会收敛到最优策略${\pi }^{\ast }$。