基于线性预测算法的PON系统动态资源调度matlab仿真
目录
1.程序功能描述
2.测试软件版本以及运行结果展示
3.部分程序
4.算法理论概述
4.1 线性预测算法
4.2 更新权重系数
5.完整程序
1.程序功能描述
在无源光网络(PON)系统中,高效的资源调度是保障网络带宽利用率与业务服务质量(QoS)的核心环节。传统静态资源调度方式因无法适配终端用户(ONU)流量的动态变化,易导致带宽浪费或业务延迟。基于线性预测算法的动态资源调度技术,通过对ONU上行流量的精准预测,实现资源的按需分配,成为解决这一问题的关键方案。
2.测试软件版本以及运行结果展示
MATLAB2022A/MATLAB2024B版本运行
预测算法和真实值对比:
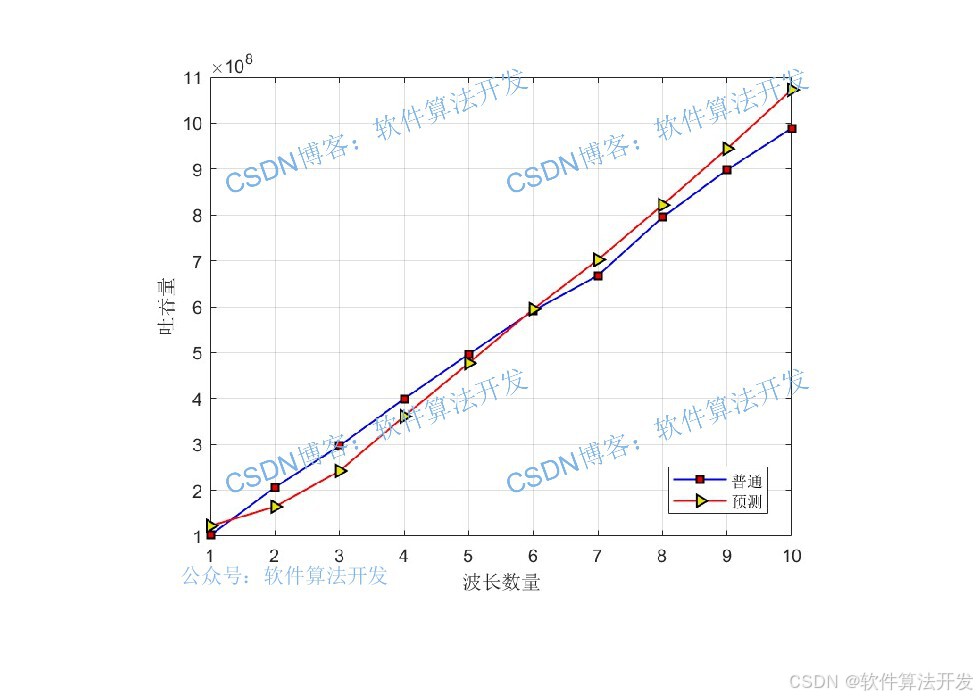
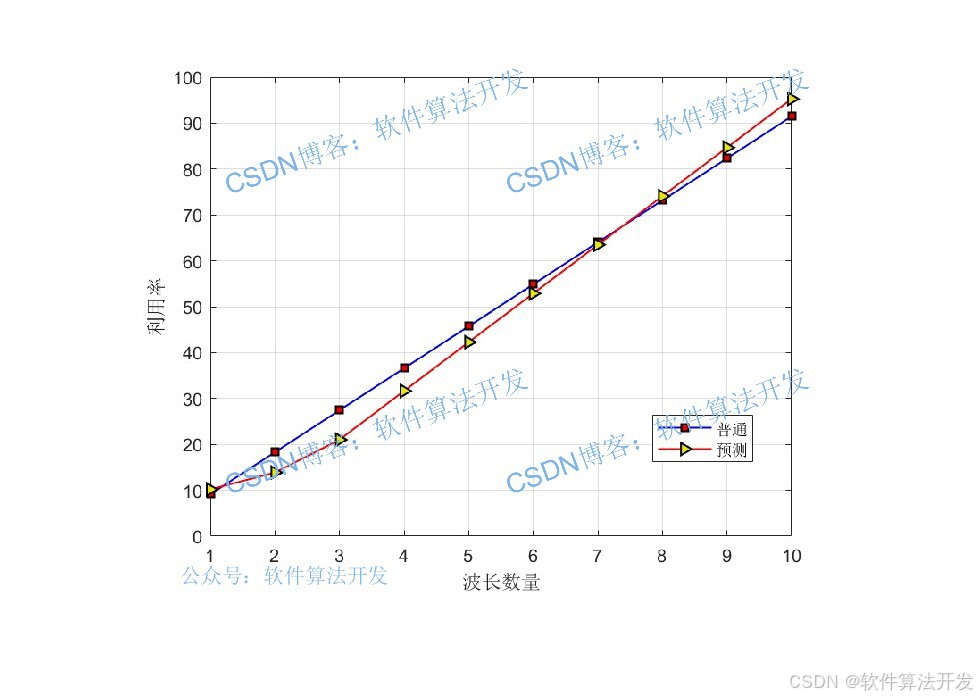
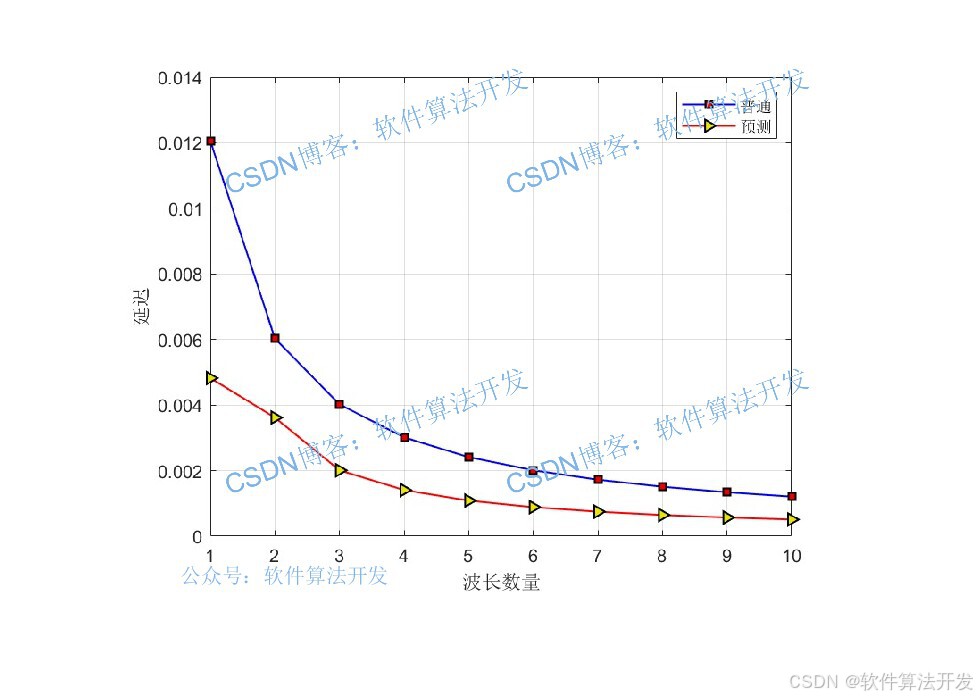
采用预测算法进行调度之后,系统的延迟改善:
3.部分程序
figure;
plot(mean(ttl1,2),'-bs',...'LineWidth',1,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.0,0.0]);%画图吐吞量
hold on
plot(ttl2,'-r>',...'LineWidth',1,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.9,0.0]);xlabel('波长数量');
ylabel('吐吞量');
grid on
legend('普通','预测');figure;
plot(mean(delay1,2),'-bs',...'LineWidth',1,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.0,0.0]);%画图延迟
hold on
plot(delay2/1e8,'-r>',...'LineWidth',1,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.9,0.0]);xlabel('波长数量');
ylabel('延迟');
grid on
legend('普通','预测');figure;
plot(mean(LYL1,2),'-bs',...'LineWidth',1,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.0,0.0]);%画图利用率
hold on
plot(LYL2,'-r>',...'LineWidth',1,...'MarkerSize',6,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.9,0.9,0.0]);xlabel('波长数量');
ylabel('利用率');
grid on
legend('普通','预测');%普通
X1 = [Lemda_num',mean(ttl1,2),mean(delay1,2),mean(LYL1,2)]%利用率提升
X2 = [Lemda_num',ttl2',delay2'/1e8,LYL2']
12_0684.算法理论概述
PON系统由光线路终端(OLT)、光分配网络(ODN)和光网络单元(ONU)三部分组成,上行方向(ONU 到 OLT)采用 “时分多址(TDMA)” 技术实现多用户共享带宽。在传统调度模式中,OLT通常根据ONU历史上报的缓存数据量分配带宽,但该方式存在明显滞后性 —— 当ONU 突发大量数据时,已分配的带宽无法满足需求,导致数据缓存堆积;而当ONU流量骤减时,已分配的带宽又会闲置,降低整体网络利用率。
基于线性预测算法的动态资源调度,核心是在“历史流量数据”与“未来流量需求”之间建立数学关联模型。通过分析ONU过往上报的缓存数据(反映实际流量),利用线性预测模型推算出未来一个或多个周期内的流量规模,再结合ONU当前实际缓存数据量,综合确定带宽分配额度。这种 “预测+实时缓存”的双重考量,既避免了滞后性导致的资源错配,又能提前预留带宽以应对突发流量,实现资源调度的动态性与精准性。
4.1 线性预测算法
线性预测算法的本质是“利用过去N个时刻的观测值,通过线性组合的方式预测未来时刻的数值”。在PON系统资源调度场景中,“观测值” 即ONU在不同轮询周期内上报的缓存数据量(记为:

根据线性预测模型,下一个时刻(n+1)的预测流量x^(n+1),是过去L个时刻观测值与对应权重系数的线性叠加,其数学公式如式所示:
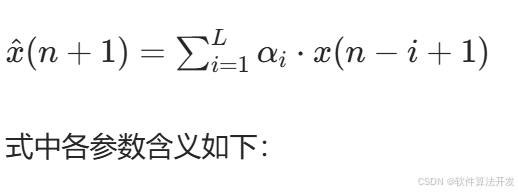

4.2 更新权重系数
为使预测模型持续适配流量变化,OLT需通过LMS算法动态调整权重系数αi,调整目标是 “最小化预测误差的均方值”(即E[e2(n)]→min,E[⋅]表示数学期望)。
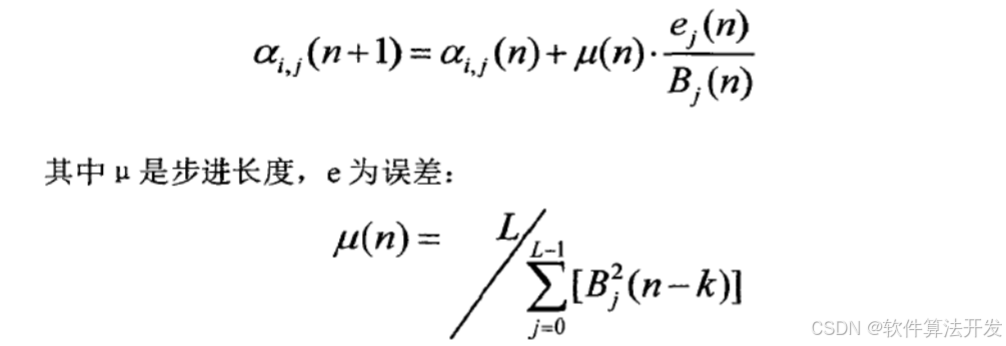
式中各参数含义如下:

5.完整程序
VVV
关注后手机上输入程序码:121
