【强化学习核心解析】特点、分类与DQN算法及嵌入式低功耗应用

引言

若对您有帮助的话，请点赞收藏加关注哦，您的关注是我持续创作的动力！有问题请私信或联系邮箱：[e-mail]

强化学习（Reinforcement Learning, RL）是机器学习三大范式（监督学习、无监督学习、强化学习）中最接近人类“试错学习”逻辑的分支——它通过智能体（Agent）与环境（Environment）的动态交互，以“延迟奖励”为反馈信号优化决策策略，最终实现目标最大化。随着嵌入式设备（如可穿戴设备、IoT节点）向“智能化+低功耗”方向发展，传统复杂RL算法因算力、内存、功耗需求高难以部署，而DQN（Deep Q-Network）作为“深度学习+强化学习”的经典融合算法，通过改进后可适配嵌入式低功耗场景，成为边缘智能决策的重要技术支撑。本文将从强化学习基础出发，聚焦DQN核心技术与嵌入式应用落地，为开发者提供从理论到实践的完整视角。

一、强化学习的核心特点：区别于传统机器学习的关键

强化学习的本质是“智能体在环境中通过试错积累经验，学习最优决策策略”，其核心特点与监督/无监督学习存在显著差异，具体可概括为4点：

1.1 试错学习（Trial-and-Error Learning）

• 核心逻辑：智能体无需预先获取“正确答案”（如监督学习的标签），而是通过主动执行动作（Action）、观察环境反馈（Reward），不断调整策略——“做得好就强化，做得差就修正”。
• 典型场景：机器人学习行走时，摔倒（负奖励）后调整关节角度，平稳行走（正奖励）后保留动作模式，最终掌握平衡策略。
• 与监督学习的差异：监督学习依赖“输入-标签”的即时反馈，强化学习依赖“动作序列-延迟奖励”的累积反馈，更贴近人类从实践中学习的过程。

1.2 延迟奖励（Delayed Reward）

• 核心逻辑：强化学习的奖励并非即时获取，而是在执行一系列动作后才能得到（即“长期奖励”），智能体需判断“当前动作对最终目标的贡献”。
• 示例：围棋AI（如AlphaGo）落子后，需等到棋局结束（赢/输）才能获得最终奖励，中间每一步落子的“价值”需通过后续局势间接评估。
• 关键挑战：如何将“延迟奖励”合理分配到每一步动作中，是强化学习的核心问题（如Q-learning通过“折扣奖励”解决该问题）。

1.3 智能体与环境的动态交互

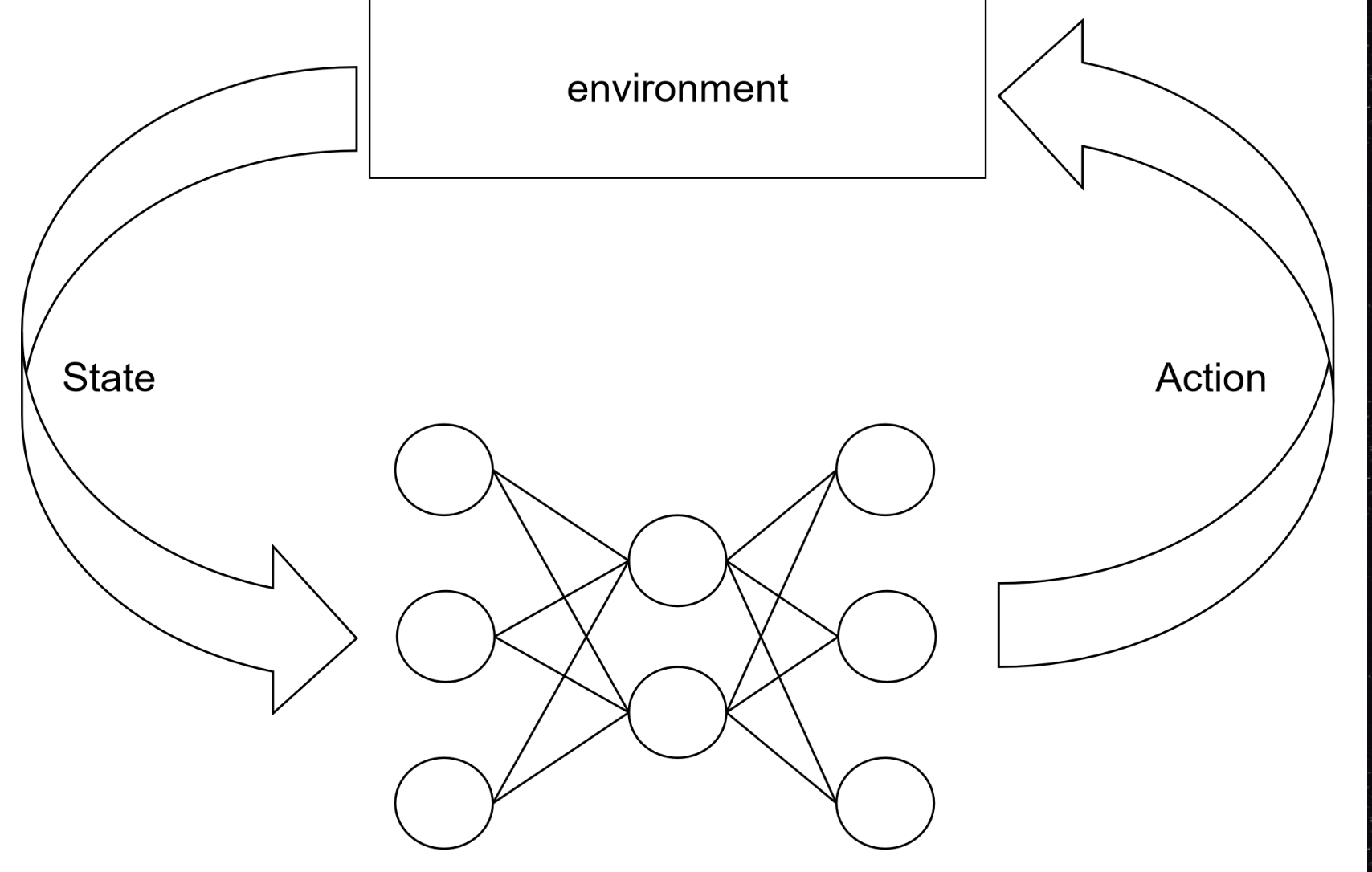
• 核心逻辑：强化学习的核心框架是“智能体→动作→环境→状态/奖励→智能体”的闭环交互，环境状态（State）会因智能体的动作动态变化，智能体的策略也会随环境反馈迭代优化。
• 数学描述：该交互过程通过马尔可夫决策过程（MDP） 建模，MDP包含5个核心要素：
  • 状态空间 ( S )：环境所有可能状态的集合（如机器人的位置、速度）；
  • 动作空间 ( A )：智能体可执行的所有动作的集合（如机器人的“前进”“转向”）；
  • 奖励函数 ( R(s,a) )：在状态 ( s ) 执行动作 ( a ) 后获得的即时奖励；
  • 状态转移概率 ( P(s’|s,a) )：在状态 ( s ) 执行动作 ( a ) 后转移到状态 ( s’ ) 的概率；
  • 折扣因子 ( \gamma )（0≤γ≤1）：衡量未来奖励的权重（γ=0仅关注即时奖励，γ=1同等重视未来奖励）。

1.4 策略优化为核心目标

• 核心逻辑：强化学习的最终目标是学习一个最优策略 ( \pi^*(a|s) )——即在任意状态 ( s ) 下，选择能最大化“长期累积奖励”的动作 ( a )。
• 策略表示：策略分为“确定性策略”（( a = \pi(s) )，每个状态对应唯一动作）和“随机性策略”（( \pi(a|s) = P(a|s) )，每个状态对应动作的概率分布），DQN等价值优化算法通过间接优化价值函数实现策略优化。

二、强化学习的分类对比：多维度拆解技术体系

强化学习可按“是否依赖环境模型”“学习目标”“动作空间类型”等维度分类，不同类别算法的适用场景、复杂度差异显著，通过表格对比可清晰区分：

2.1 按“是否基于环境模型”分类（核心分类维度）

分类	核心思想	优缺点	代表算法	适用场景
基于模型（Model-Based RL）	先学习环境模型（状态转移概率 ( P ) + 奖励函数 ( R )），再基于模型优化策略	优点：可通过模型模拟环境，减少与真实环境交互次数（降低试错成本）； 缺点：模型建模难度高，模型误差会导致策略失效	Dyna-Q、蒙特卡洛树搜索（MCTS，如AlphaGo核心）	环境交互成本高的场景（如工业机器人试错易损坏设备）
无模型（Model-Free RL）	不建模环境，直接通过与环境交互学习策略/价值函数	优点：无需建模，适用于复杂未知环境； 缺点：需大量与环境交互，试错成本高	Q-learning、DQN、策略梯度（PG）、PPO	环境简单/交互成本低的场景（如游戏、嵌入式轻量决策）

2.2 按“学习目标”分类（策略优化 vs 价值优化）

分类	核心思想	优缺点	代表算法	动作空间适配
价值优化（Value-Based RL）	学习“状态/状态-动作的价值”（如Q值），通过价值函数间接推导策略（如选择价值最大的动作）	优点：决策稳定，易实现； 缺点：仅适用于离散动作空间，难以处理连续动作	Q-learning、DQN、Double DQN	离散动作（如游戏“上下左右”、嵌入式设备“开/关/调节档位”）
策略优化（Policy-Based RL）	直接参数化策略（如用神经网络表示策略），通过梯度上升最大化累积奖励	优点：适用于连续动作空间，策略输出更直接； 缺点：训练不稳定（奖励波动大），易陷入局部最优	策略梯度（PG）、近端策略优化（PPO）、DDPG	连续动作（如机器人关节角度控制、无人机飞行姿态调节）
演员-评论家（Actor-Critic RL）	结合价值优化（Critic评估价值）和策略优化（Actor执行策略），用价值函数减少策略梯度方差	优点：兼顾连续动作适配性和训练稳定性； 缺点：模型复杂度高，需同步训练两个网络	DDPG、TD3、SAC	连续动作场景（如工业控制、自动驾驶）

2.3 按“探索与利用策略”分类（平衡试错与收益的关键）

分类	核心思想	优缺点	适用场景
ε-贪婪策略（ε-greedy）	以概率 ( 1-\varepsilon ) 选择当前价值最大的动作（利用），以概率 ( \varepsilon ) 随机选择动作（探索），( \varepsilon ) 随训练迭代减小	优点：实现简单，易调节探索强度； 缺点：后期仍有随机探索，可能选择差动作	多数Model-Free算法（如DQN、Q-learning）
上限置信区间（UCB）	选择“价值估计值 + 不确定性惩罚项”最大的动作，不确定性随尝试次数增加而降低	优点：主动探索高潜力但尝试少的动作，探索更高效； 缺点：计算复杂度高，依赖价值估计的不确定性量化	多臂老虎机问题、MCTS
玻尔兹曼探索（Boltzmann Exploration）	按动作价值的softmax概率选择动作，温度参数 ( T ) 控制探索强度（( T ) 大则探索强，( T ) 小则利用强）	优点：探索强度平滑变化，避免极端随机； 缺点：温度参数调优复杂	价值优化算法（如Q-learning）的进阶探索策略

2.4 按“动作空间类型”分类（场景适配的关键）

分类	核心特点	代表算法	典型应用场景
离散动作RL	动作空间有限且离散（如“0/1”“上下左右”），价值函数易建模	Q-learning、DQN、Double DQN	游戏（Atari）、嵌入式设备档位控制（如灯光亮度3档调节）
连续动作RL	动作空间无限且连续（如“01之间的电压值”“-ππ的角度”），需参数化策略	DDPG、PPO、SAC	机器人控制（关节角度）、无人机飞行控制、工业设备参数调节

三、DQN算法：深度强化学习的“入门标杆”与核心技术

DQN（Deep Q-Network）由DeepMind于2013年提出，首次将深度学习（神经网络） 与Q-learning（传统价值优化算法） 结合，解决了传统Q-learning在“高维状态空间”（如游戏像素画面）中无法建模的问题，开启了深度强化学习的新时代。

3.1 DQN的核心背景：为什么需要DQN？

传统Q-learning的局限性：

• 传统Q-learning用“Q表格”存储所有“状态-动作对”的Q值（( Q(s,a) ) 表示在状态 ( s ) 执行动作 ( a ) 的长期累积奖励）；
• 当状态空间高维（如Atari游戏的210×160×3像素画面，状态数达 ( 256^{210×160×3} )）时，Q表格无法存储（维度灾难）；
• DQN的解决方案：用深度神经网络（CNN/MLP）近似Q函数，即 ( Q(s,a;\theta) )，其中 ( \theta ) 是网络参数，通过训练网络拟合真实Q值。

3.2 DQN的核心原理：从Q-learning到深度近似

3.2.1 基础：Q-learning的更新规则

Q-learning的核心是通过“时序差分（TD）误差”更新Q值，目标是让当前Q值逼近“即时奖励+未来最优Q值”，更新公式如下：
[ Q(s_t,a_t) \leftarrow Q(s_t,a_t) + \alpha \cdot \left[ r_t + \gamma \cdot \max_{a’} Q(s_{t+1},a’) - Q(s_t,a_t) \right] ]
其中：

• ( \alpha )（0<α<1）：学习率，控制每次更新的幅度；
• ( r_t )：在状态 ( s_t ) 执行动作 ( a_t ) 获得的即时奖励；
• ( \max_{a’} Q(s_{t+1},a’) )：状态 ( s_{t+1} ) 下所有动作的最大Q值（即未来最优价值）。

3.2.2 DQN的改进：用神经网络近似Q函数

DQN将Q-learning的“Q表格”替换为“Q网络”，网络输入为环境状态 ( s_t )（如游戏像素），输出为每个动作 ( a ) 对应的Q值 ( Q(s_t,a;\theta) )，此时更新规则变为“最小化TD误差的平方损失”：
[ \mathcal{L}(\theta) = \mathbb{E}_{(s,a,r,s’) \sim \mathcal{D}} \left[ \left( y_t - Q(s,a;\theta) \right)^2 \right] ]
其中：

• ( \mathcal{D} ) 是经验回放池（Replay Buffer），存储智能体与环境交互的“经验样本”( (s,a,r,s’) )；
• ( y_t = r + \gamma \cdot \max_{a’} Q’(s’,a’;\theta^-) ) 是“目标Q值”，( Q’ ) 是目标Q网络，参数 ( \theta^- ) 固定一段时间后从当前Q网络同步（非实时更新）。

3.3 DQN的两大关键技术：解决训练稳定性问题

DQN的成功依赖“经验回放”和“目标Q网络”两大创新，这两项技术直接解决了传统深度强化学习的训练不稳定问题：

3.3.1 经验回放（Experience Replay）

• 核心问题：智能体与环境交互的样本具有“时间相关性”（如连续帧的游戏画面高度相似），直接用连续样本训练会导致网络参数震荡（梯度更新方向不稳定）。
• 解决方案：
  1. 智能体与环境交互时，将每次的经验样本 ( (s,a,r,s’) ) 存储到容量固定的经验回放池 ( \mathcal{D} )；
  2. 训练时从 ( \mathcal{D} ) 中随机抽样一批样本（如32个）更新Q网络；
• 优势：
  • 打破样本时间相关性，使样本满足独立同分布（IID）假设，符合深度学习训练要求；
  • 同一经验样本可被多次复用，提高数据利用效率（尤其适用于嵌入式场景，减少数据采集量）。

3.3.2 目标Q网络（Target Q-Network）

• 核心问题：若直接用当前Q网络计算目标Q值 ( y_t = r + \gamma \cdot \max_{a’} Q(s’,a’;\theta) )，则目标Q值与待更新的网络参数 ( \theta ) 强相关，导致“目标移动”（目标Q值随 ( \theta ) 变化），训练易发散。
• 解决方案：
  1. 维护两个结构完全相同但参数独立的Q网络：当前Q网络（( Q(s,a;\theta) )） 和 目标Q网络（( Q’(s,a;\theta^-) )）；
  2. 训练时，目标Q网络的参数 ( \theta^- ) 不实时更新，而是每隔 ( C ) 步（如1000步）从当前Q网络同步一次（( \theta^- \leftarrow \theta )）；
• 优势：固定目标Q值的计算基准，减少训练波动，提升网络收敛稳定性。

3.4 DQN的训练流程：Step-by-Step拆解

DQN的训练过程可分为“交互采样”和“网络更新”两大阶段，具体步骤如下：

1. 初始化：

   • 初始化当前Q网络 ( Q(\theta) ) 和目标Q网络 ( Q’(\theta^-) )，令 ( \theta^- = \theta )；
   • 初始化经验回放池 ( \mathcal{D} )（容量如1e5~1e6）；
   • 初始化环境状态 ( s_0 )（如游戏第一帧画面）。

2. 交互采样（探索阶段）：

   • 对当前状态 ( s_t )，用 ( \varepsilon )-greedy策略选择动作 ( a_t )：
     • 以概率 ( 1-\varepsilon ) 选择 ( a_t = \arg\max_a Q(s_t,a;\theta) )（利用）；
     • 以概率 ( \varepsilon ) 随机选择动作 ( a_t )（探索）；
   • 执行动作 ( a_t )，观察环境反馈的即时奖励 ( r_t ) 和下一状态 ( s_{t+1} )；
   • 将经验样本 ( (s_t,a_t,r_t,s_{t+1}) ) 存入经验回放池 ( \mathcal{D} )；
   • 令 ( s_t = s_{t+1} )，若 ( s_{t+1} ) 是终止状态，则重新初始化 ( s_t )。

3. 网络更新（学习阶段）：

   • 当经验回放池容量达到阈值（如1000样本）后，开始训练：
     • 从 ( \mathcal{D} ) 中随机抽样一批样本 ( {(s_i,a_i,r_i,s’i)}{i=1}^B )（( B ) 为批次大小，如32）；
     • 计算每个样本的目标Q值 ( y_i )：
       • 若 ( s’_i ) 是终止状态，( y_i = r_i )（无未来奖励）；
       • 否则，( y_i = r_i + \gamma \cdot \max_{a’} Q’(s’_i,a’;\theta^-) )；
     • 计算当前Q值 ( Q(s_i,a_i;\theta) )（仅选择动作 ( a_i ) 对应的输出）；
     • 用梯度下降法最小化损失 ( \mathcal{L}(\theta) = \frac{1}{B} \sum_{i=1}^B (y_i - Q(s_i,a_i;\theta))^2 )，更新当前Q网络参数 ( \theta )；
   • 每隔 ( C ) 步，同步目标Q网络参数：( \theta^- \leftarrow \theta )。

4. 迭代终止：

   • 重复步骤2~3，直到累积奖励达到预设阈值（如游戏通关）或训练步数达到上限。

3.5 DQN的改进算法：解决原DQN的局限性

原DQN存在“Q值过估计”（目标Q值偏高）、“未区分状态价值与动作优势”等问题，后续改进算法进一步提升性能，核心改进方向如下：

改进算法	核心改进点	解决的问题	性能提升效果
Double DQN	用当前Q网络选择最优动作，目标Q网络计算Q值（( y = r + \gamma \cdot Q’(s’,\arg\max_a Q(s’,a;\theta);\theta^-) )）	原DQN的“max”操作导致Q值过估计（高估动作实际价值）	降低过估计幅度，提升策略稳定性
Dueling DQN	将Q网络拆分为“状态价值网络 ( V(s) )”和“动作优势网络 ( A(s,a) )”，Q值=V(s)+(A(s,a)-mean(A(s,a)))	原DQN需评估所有动作Q值，Dueling DQN可直接学习状态价值，适合状态相似但动作影响小的场景	减少动作评估开销，提升高维状态下的学习效率
Prioritized Experience Replay（PER）	按TD误差大小给经验样本分配优先级，误差大的样本被抽样概率更高	原DQN随机抽样，重要样本（误差大）利用率低	加速训练收敛，减少训练步数
Rainbow DQN	融合Double DQN、Dueling DQN、PER、多步TD学习、分布式Q值等6种改进	综合解决过估计、样本利用率低、单步奖励偏差等问题	Atari游戏平均得分超原DQN 100%+

四、DQN在嵌入式低功耗场景的应用：挑战与优化策略

嵌入式低功耗设备（如可穿戴设备、IoT传感器节点）的核心约束是“算力有限（CPU主频低、无独立GPU）、内存/存储小、电池供电（功耗敏感）”，直接部署原始DQN会面临严重瓶颈，需从“算法优化”“模型压缩”“硬件适配”三方面突破。

4.1 嵌入式低功耗设备的核心约束

约束类型	具体表现	对DQN的影响
算力约束	CPU主频多为几百MHz（如ARM Cortex-M系列），无GPU/TPU加速，浮点运算能力弱	DQN的神经网络前向推理耗时久（如复杂CNN需数百毫秒），无法满足实时决策需求（如可穿戴设备的100ms内响应）
内存/存储约束	内存（RAM）多为几十KB几MB，存储（Flash）多为几百KB几十MB	原始DQN的网络参数（如CNN的百万级参数）无法存入内存，经验回放池需大量存储样本，超出Flash容量
功耗约束	电池容量小（如可穿戴设备的100~500mAh），需低功耗运行（如μA级电流）	DQN的频繁神经网络计算会导致功耗骤升（如推理时电流达mA级），电池续航从几天缩短至几小时
实时性约束	嵌入式场景多需即时决策（如工业传感器的异常响应、可穿戴设备的动作识别）	DQN训练阶段需大量交互，嵌入式设备无法在线训练；推理阶段若耗时超阈值，会导致决策滞后

4.2 DQN在嵌入式低功耗场景的典型应用

尽管存在约束，但DQN通过优化后可在“轻量级决策场景”落地，典型应用如下：

4.2.1 智能家居低功耗设备控制

• 场景需求：智能家居传感器（如人体存在传感器、光照传感器）需根据环境变化和用户习惯，优化设备运行模式（如灯光亮度、空调温度），同时降低功耗。
• DQN的作用：
  • 状态 ( s )：传感器采集的“光照强度、人体存在状态、当前能耗”；
  • 动作 ( a )：“灯光亮度1_{3档、空调温度24}26℃”（离散动作）；
  • 奖励 ( r )：“用户舒适度评分（正奖励）- 能耗值（负奖励）”；
• 优势：DQN学习用户习惯后，可在“舒适度”和“低功耗”间找到最优平衡，如无人时自动调低亮度，降低能耗30%+。

4.2.2 可穿戴设备的健康监测与功耗调节

• 场景需求：可穿戴设备（如智能手环）需实时监测用户行为（如步行、跑步、睡眠），并根据监测结果调节传感器采样频率（如睡眠时降低心率采样频率以省电）。
• DQN的作用：
  • 状态 ( s )：“心率值、运动加速度、当前采样频率、剩余电量”；
  • 动作 ( a )：“采样频率1Hz/5Hz/10Hz”（离散动作）；
  • 奖励 ( r )：“监测准确率（正奖励）- 采样功耗（负奖励）”；
• 优势：传统固定采样频率易导致“高功耗”或“低准确率”，DQN可动态调节采样频率，在保证90%+监测准确率的同时，降低设备功耗40%+。

4.2.3 工业物联网（IIoT）低功耗节点控制

• 场景需求：工业场景的低功耗传感器节点（如设备温度传感器、振动传感器）需根据设备运行状态，优化数据传输频率（如异常时高频传输，正常时低频传输），减少无线传输功耗（无线传输是IIoT节点的主要功耗来源）。
• DQN的作用：
  • 状态 ( s )：“设备温度、振动幅度、传输链路质量、剩余电量”；
  • 动作 ( a )：“传输频率1次/分钟、1次/5分钟、1次/10分钟”；
  • 奖励 ( r )：“异常检测成功率（正奖励）- 传输功耗（负奖励）”；
• 优势：DQN可学习设备故障模式，在故障高发期提高传输频率（保证检测率），正常期降低频率（节省功耗），延长节点续航从1年至2年+。

4.3 DQN的嵌入式低功耗优化策略

针对嵌入式设备的约束，需从“算法简化”“模型压缩”“硬件适配”三方面对DQN进行优化，具体策略如下：

4.3.1 算法简化：降低计算与存储开销

• 离线预训练+在线微调：

  • 核心逻辑：在服务器端（高算力）完成DQN的主要训练（利用大量样本优化网络参数），嵌入式设备仅加载预训练模型，通过“在线微调”适配具体场景（如用户习惯差异），避免嵌入式端的大量交互采样与训练计算；
  • 优势：嵌入式端仅需少量参数更新（如微调最后一层），计算量减少90%+，无需存储经验回放池（仅存储少量微调样本）。

• 简化经验回放机制：

  • 若需嵌入式端在线训练，采用“小型经验池”（如容量100~1000，而非原DQN的1e5），并使用“先进先出（FIFO）”替换PER（优先级经验回放计算复杂）；
  • 优势：存储开销从几百MB降至几KB，抽样计算量减少80%+。

• 降低动作空间维度：

  • 将连续动作离散化（如温度控制从20~30℃离散为24/26/28℃三档），或减少动作数量（如仅保留核心动作）；
  • 优势：Q网络输出维度降低（如从10维降至3维），推理计算量减少60%+。

4.3.2 模型压缩：减小网络体积与推理功耗

• 量化（Quantization）：

  • 核心逻辑：将32位浮点数（FP32）参数/激活值转换为16位（FP16）、8位（INT8）甚至4位（INT4）整数，降低内存占用和计算功耗；
  • 实践方案：采用TensorFlow Lite或PyTorch Mobile的量化工具，如INT8量化可使模型体积减少75%，推理功耗降低50%+（嵌入式设备整数运算比浮点运算更高效）；
  • 注意：需进行“量化感知训练（QAT）”，避免量化导致的精度损失（如DQN决策准确率下降不超过5%）。

• 剪枝（Pruning）：

  • 核心逻辑：移除神经网络中冗余的权重（如接近0的权重）和神经元，保留核心结构；
  • 实践方案：采用“结构化剪枝”（如剪枝整个卷积核或通道，而非单个权重），避免非结构化剪枝的不规则计算（嵌入式设备不支持稀疏计算）；
  • 优势：剪枝后模型参数减少50%~70%，推理速度提升40%+，且精度损失可控（如Atari游戏得分下降<10%）。

• 轻量化网络结构设计：

  • 用轻量级神经网络替换原DQN的复杂CNN/MLP，如：
    • 卷积层采用MobileNet的“深度可分离卷积”（将标准卷积拆分为深度卷积和点卷积，计算量减少8~9倍）；
    • 全连接层用“瓶颈层”（如减少神经元数量，从1024降至256）；
    • 避免使用池化层（计算简单但易丢失细节），改用步长卷积；
  • 示例：原DQN用VGG16作为Q网络（参数138M），替换为MobileNetV2（参数3.5M），模型体积减少97%，推理耗时从500ms降至50ms（ARM Cortex-M7平台）。

4.3.3 硬件适配：利用嵌入式专用硬件加速

• 选择低功耗AI加速芯片：

  • 嵌入式设备搭载专用AI加速模块，如：
    • ARM Cortex-M系列的“CMSIS-NN”（专为神经网络优化的软件库，加速INT8推理）；
    • 低功耗NPU（神经网络处理单元），如瑞萨的DA1470x（集成NPU，INT8推理功耗仅5μA/MHz）、意法半导体的STM32H7（支持硬件浮点运算，加速FP16推理）；
  • 优势：AI加速硬件可使DQN推理速度提升3~10倍，功耗降低60%+（如Cortex-M7+CMSIS-NN的INT8推理比纯CPU快5倍）。

• 功耗感知的推理调度：

  • 根据嵌入式设备的剩余电量动态调整推理频率，如：
    • 电量>50%：正常推理（如10次/秒）；
    • 电量20%~50%：降低推理频率（如5次/秒）；
    • 电量<20%：仅保留核心决策（如1次/秒）；
  • 优势：在保证基本功能的前提下，最大化电池续航。

五、总结

强化学习以“试错学习”“延迟奖励”“动态交互”为核心特点，通过MDP框架建模智能体与环境的决策过程，按“是否基于模型”“动作空间类型”等维度可分为多类算法，其中DQN作为深度强化学习的经典算法，通过“经验回放”和“目标Q网络”解决了高维状态空间的决策问题。

在嵌入式低功耗场景中，DQN需突破“算力、内存、功耗”三大约束，通过“离线预训练+在线微调”简化算法、“量化/剪枝/轻量网络”压缩模型、“AI加速硬件+功耗调度”适配硬件，最终在智能家居、可穿戴设备、工业IoT等场景实现“智能化决策+低功耗运行”的平衡。