《考研408数据结构》第六章(5.1+5.2+5.3树、二叉树、线索二叉树)复习笔记
一、树
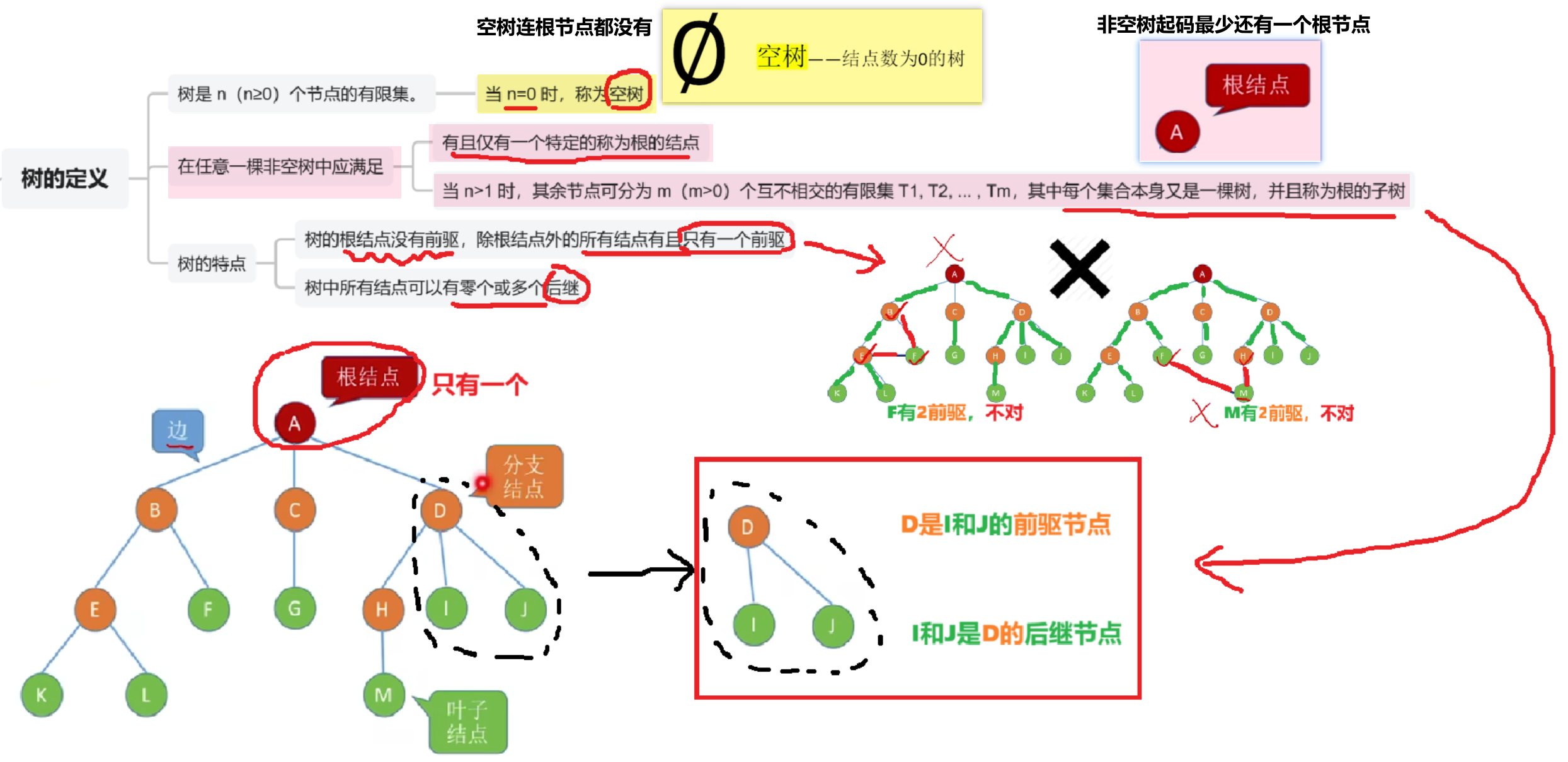
1、树的定义
计算机专业的应该都学过,只需要略微回顾一下这些名词就行;跨考的看一下这个思维导图应该也能理解
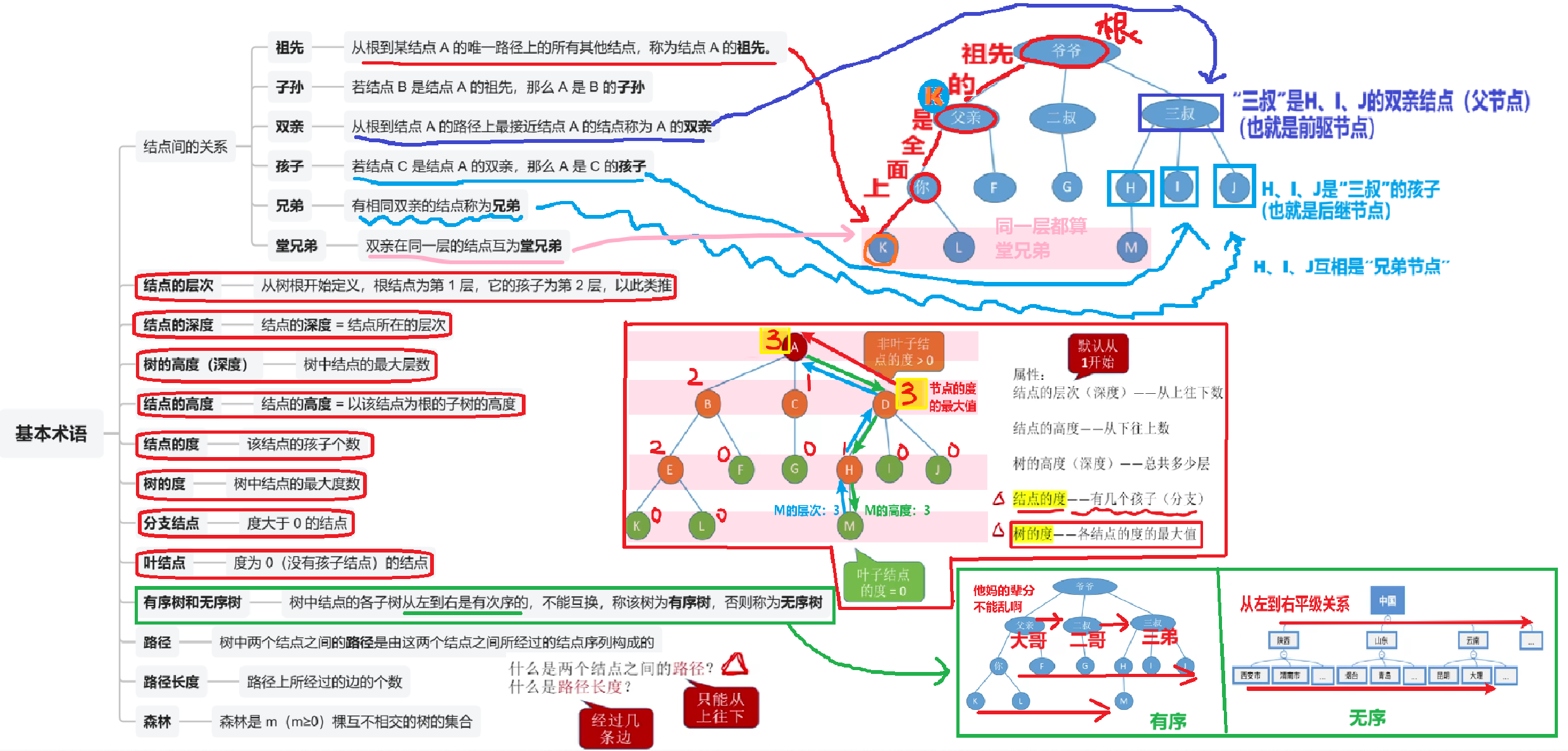
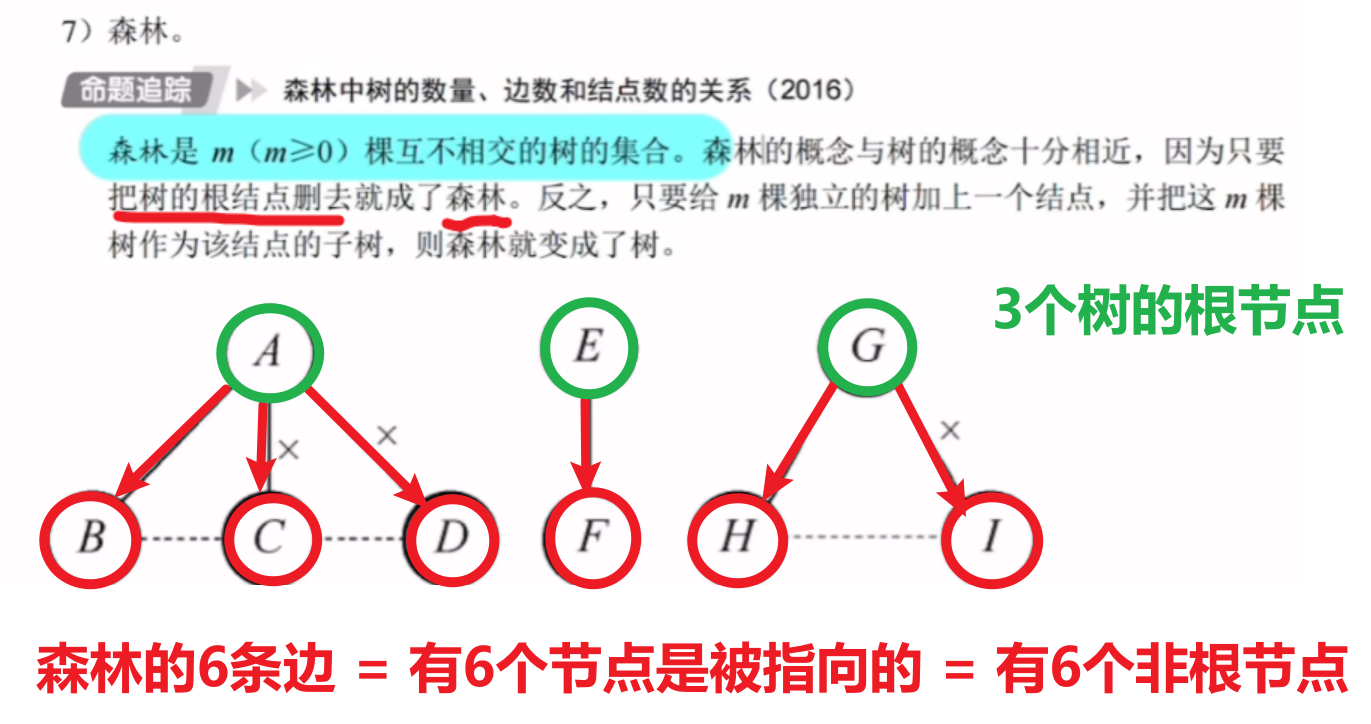
2、其他基本术语
放大来看,过一遍就行,都是很基础的概念
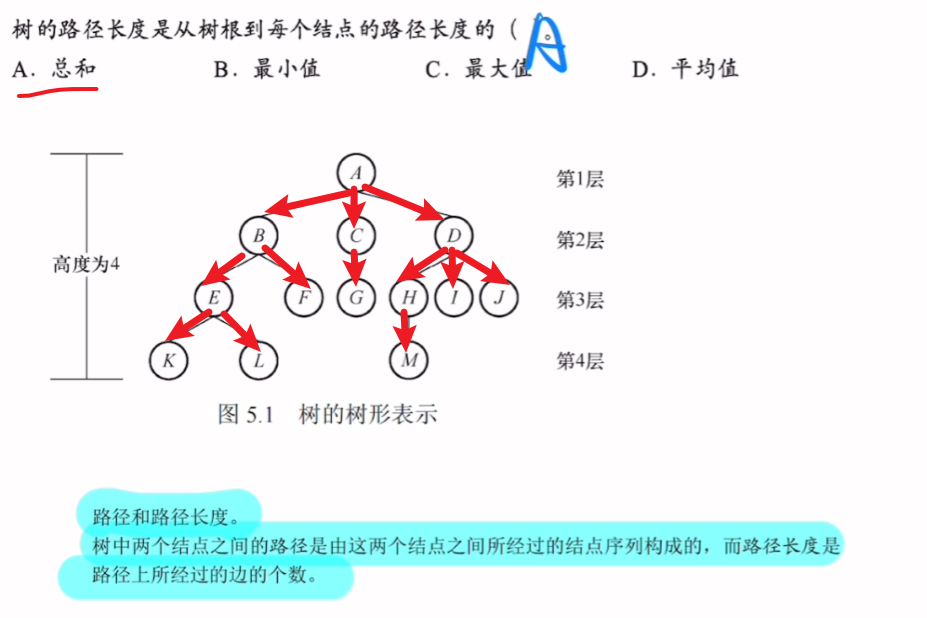
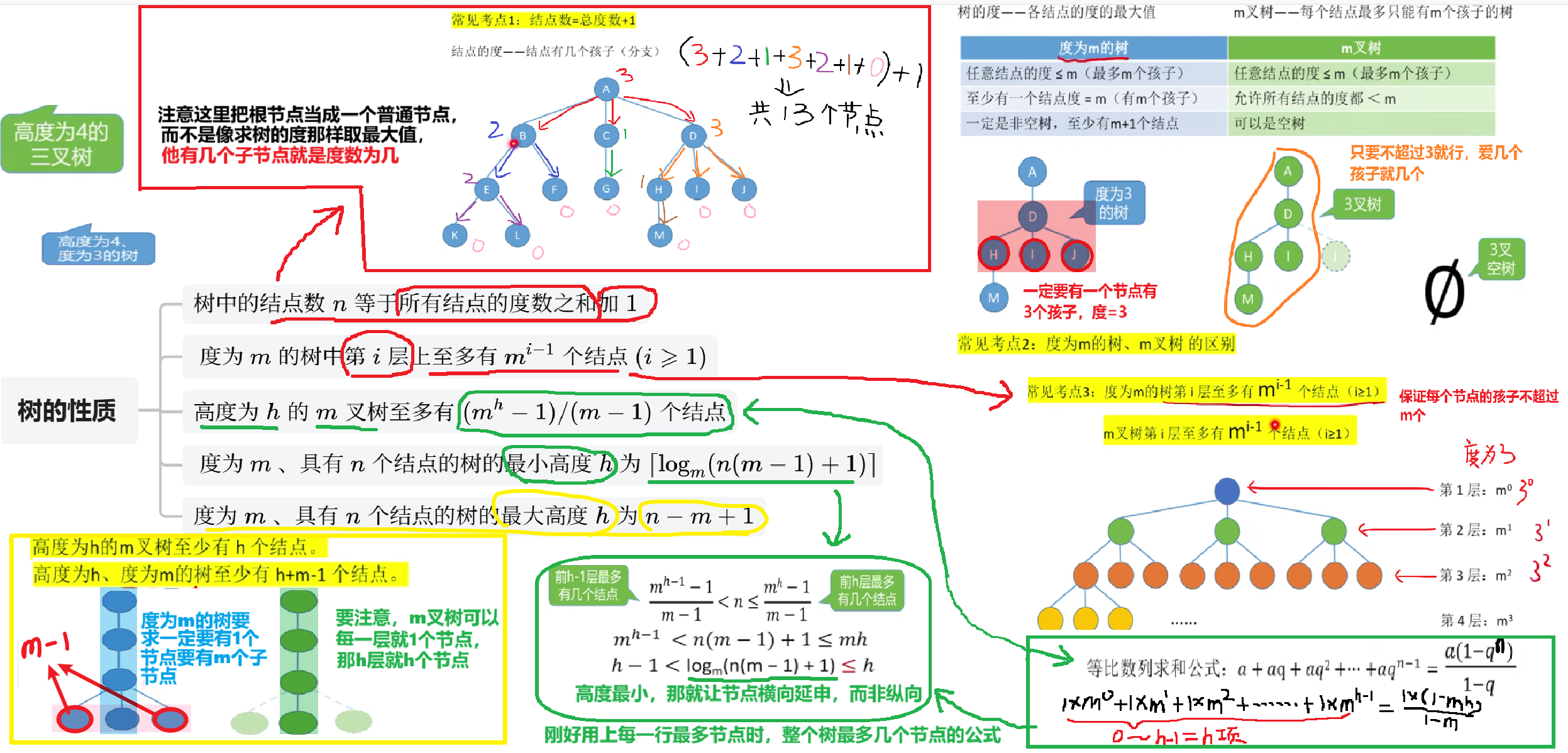
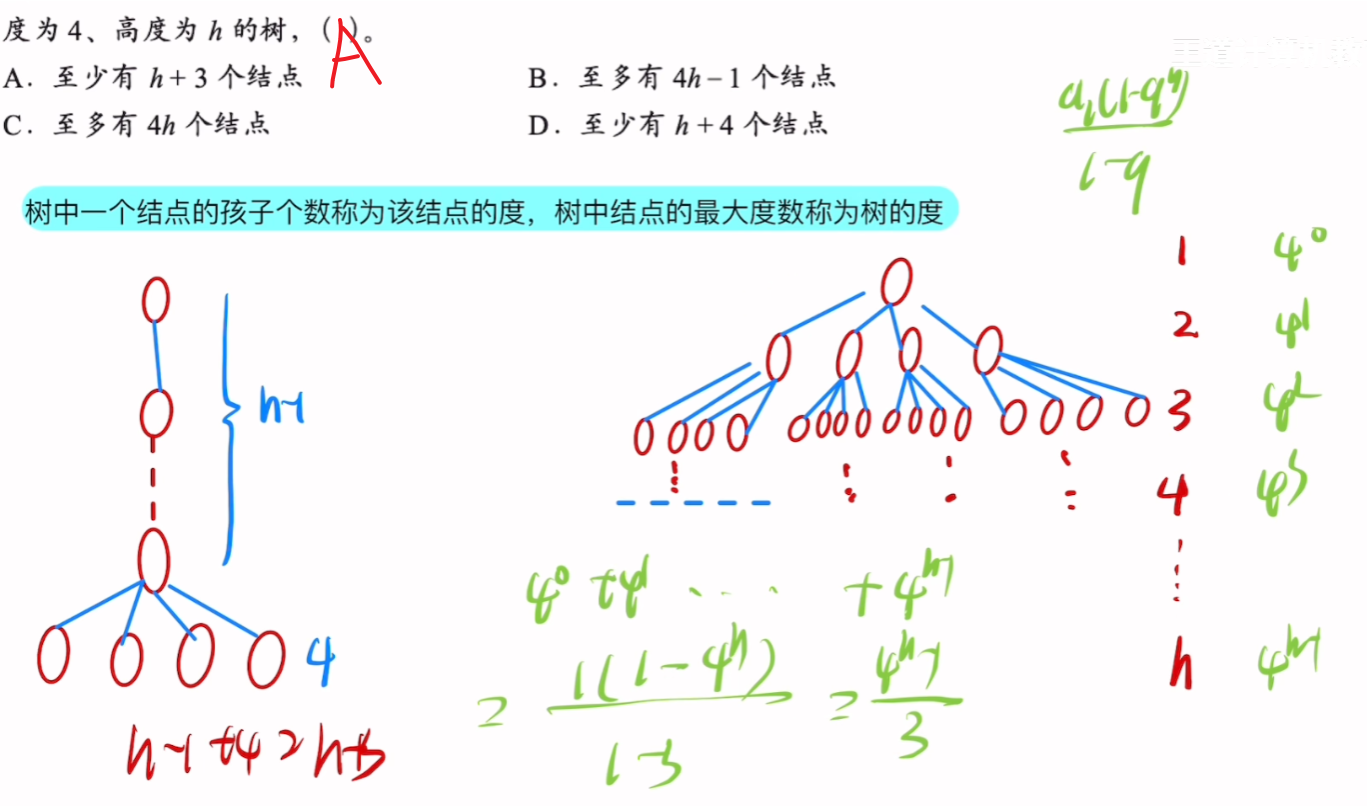
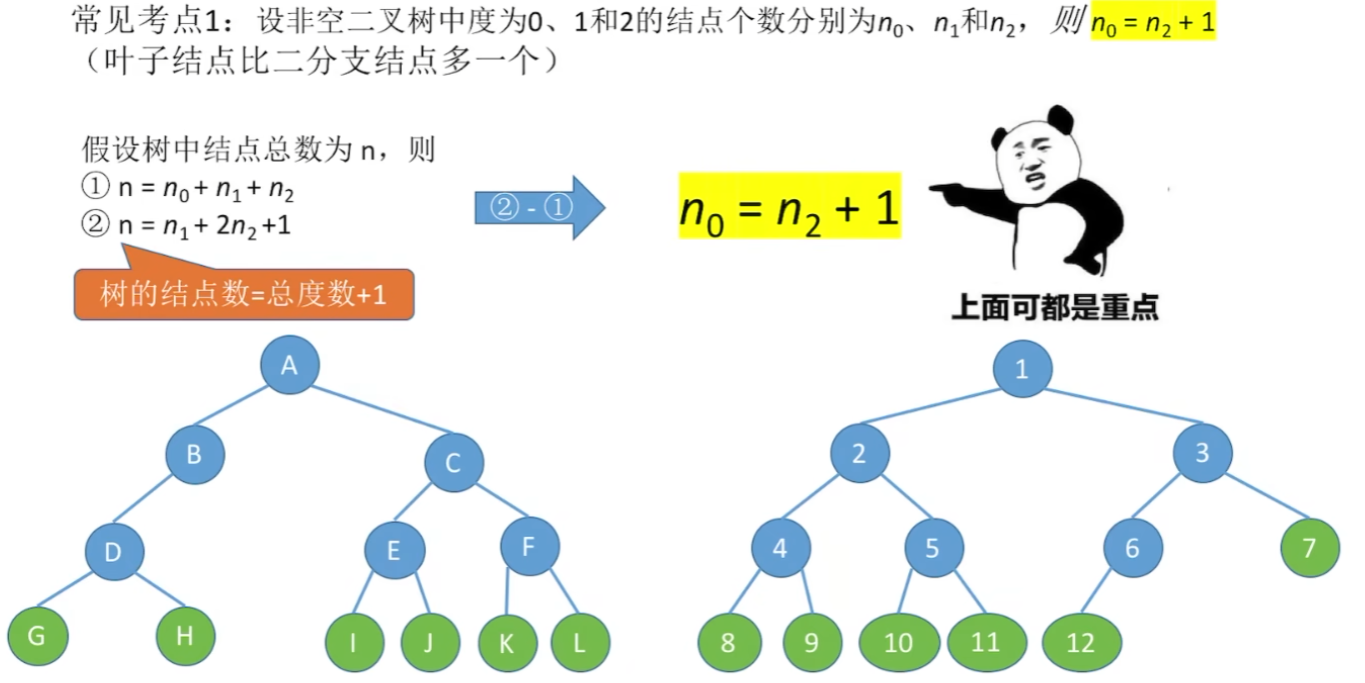
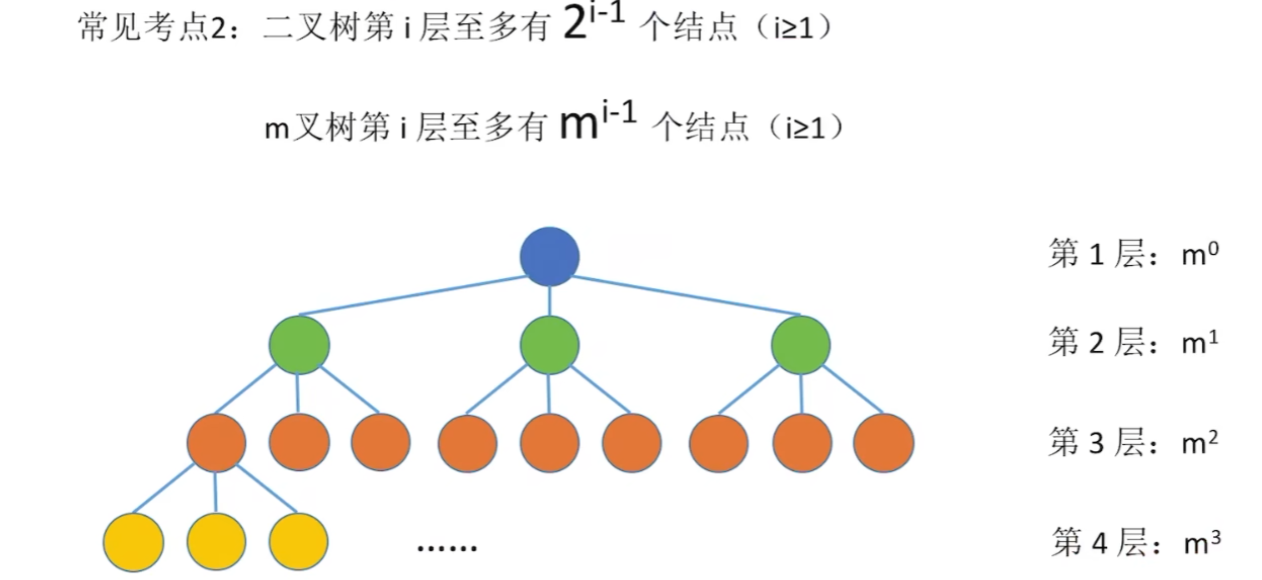
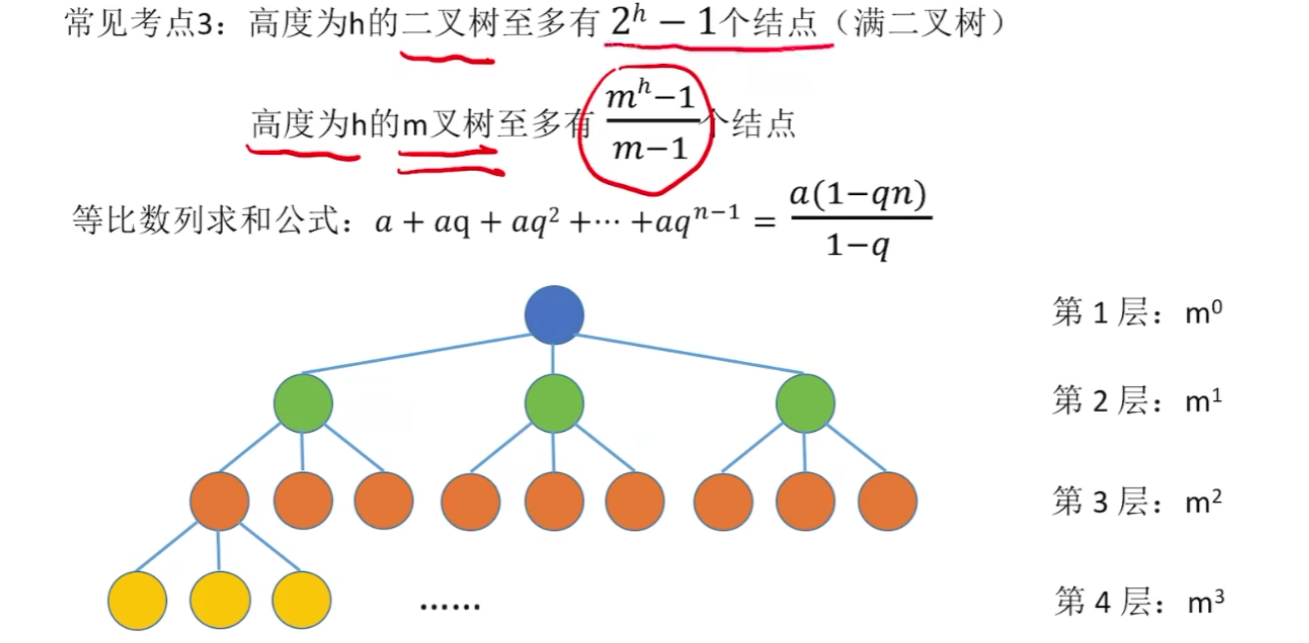
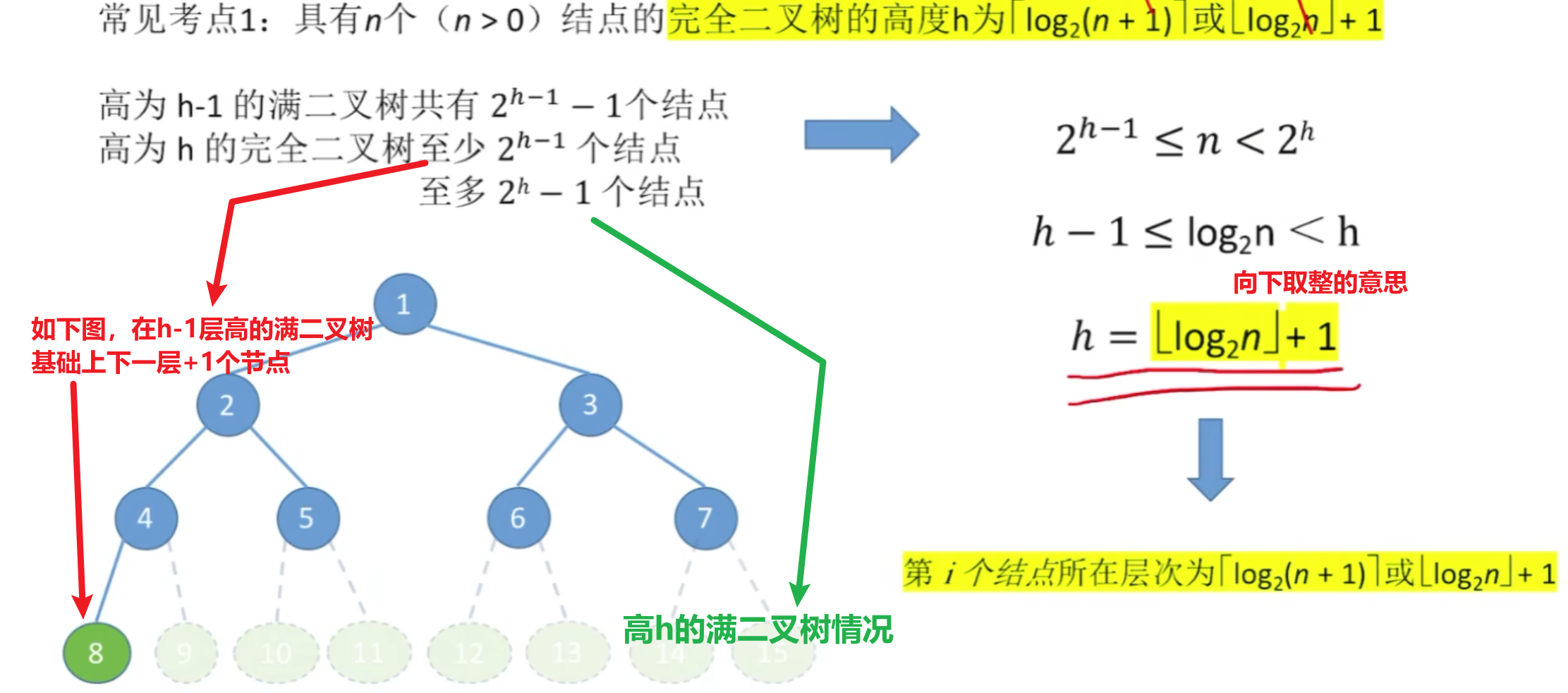
3、树的常考性质计算
虽然我的图画的很丑。。。但是我觉得这些性质不需要花太多图和文笔来解释,就这么几个公式概念之间用一个图集合起来,应该都看得懂吧。。。?
;
;
【重点注意!!】
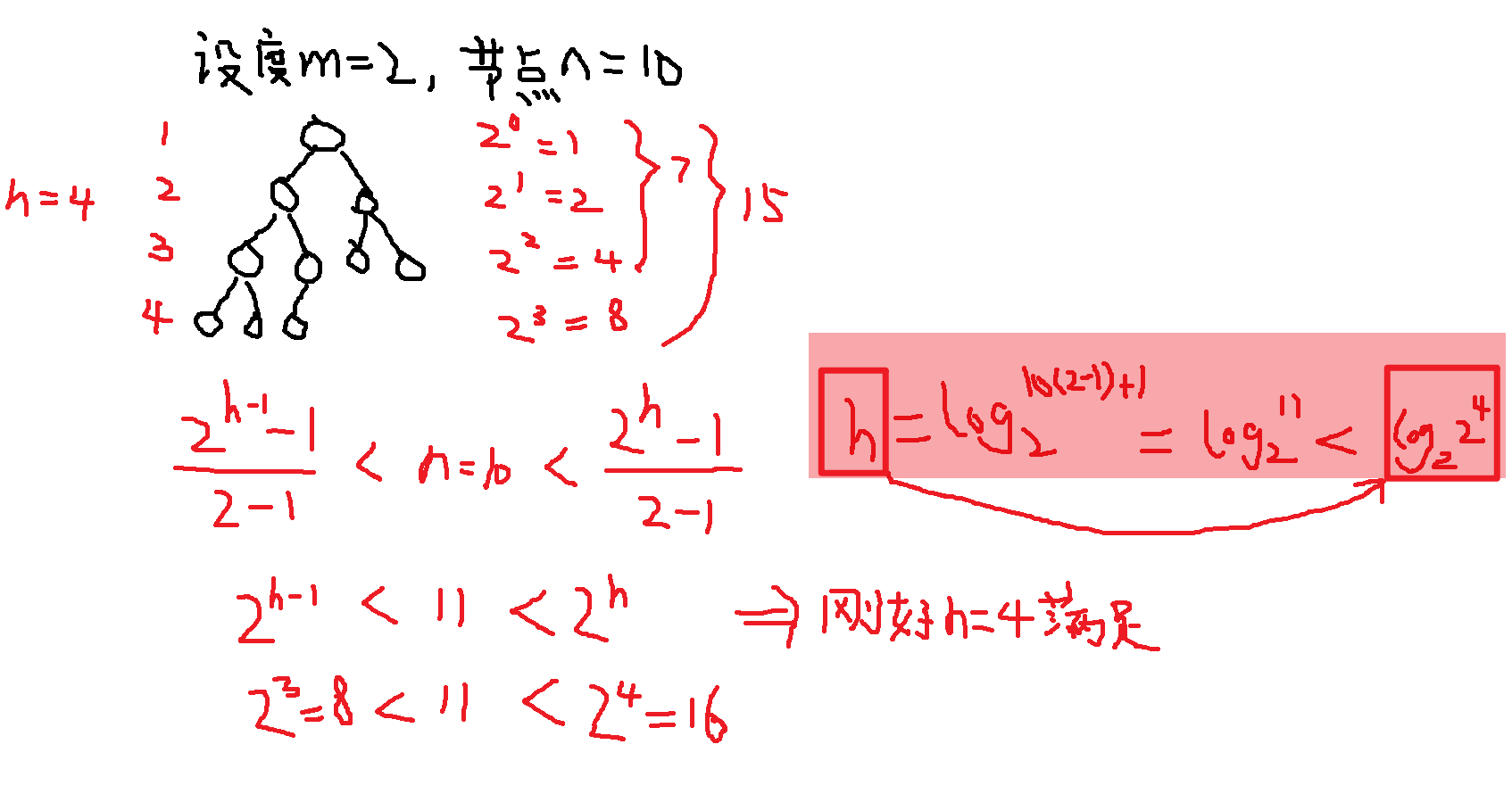
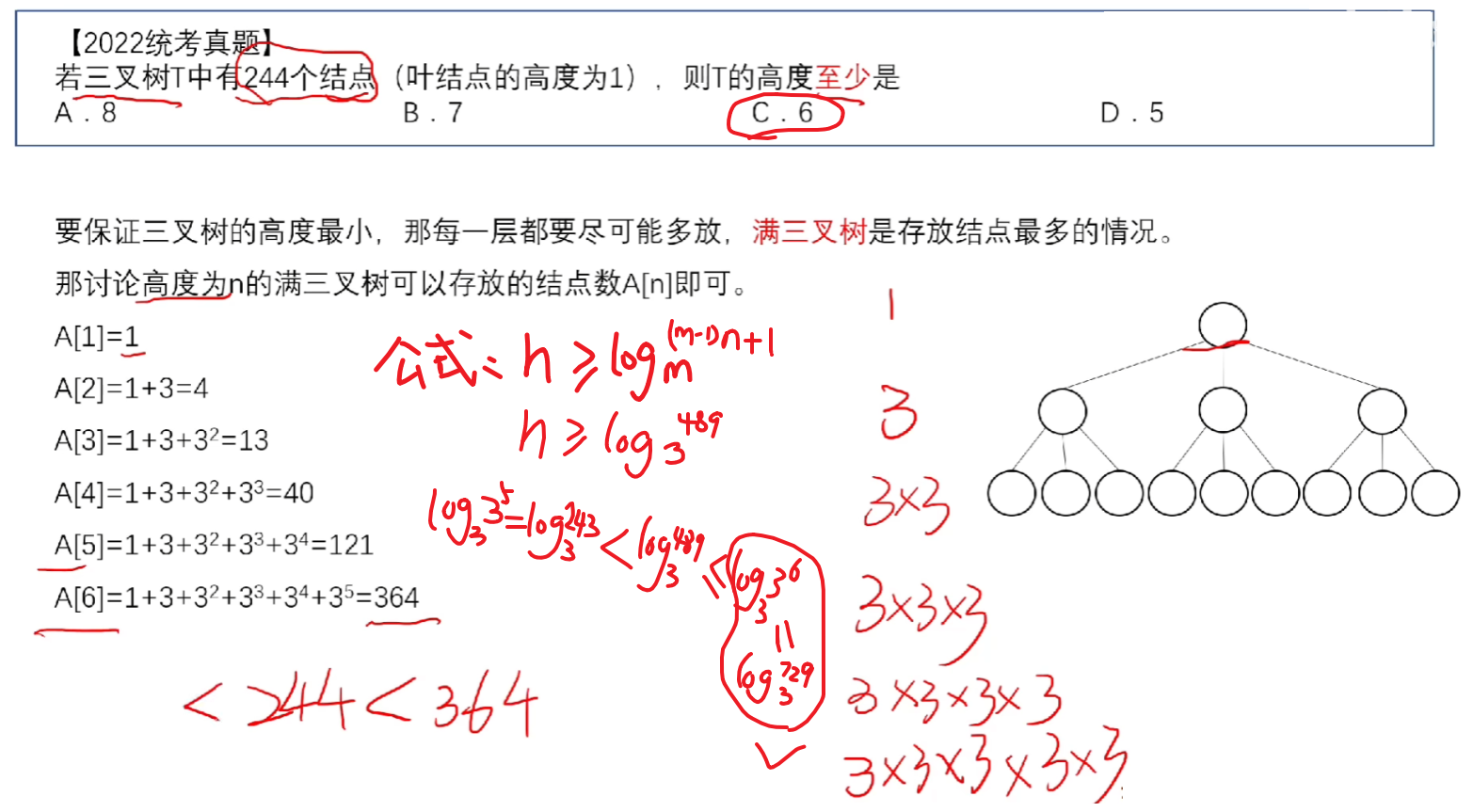
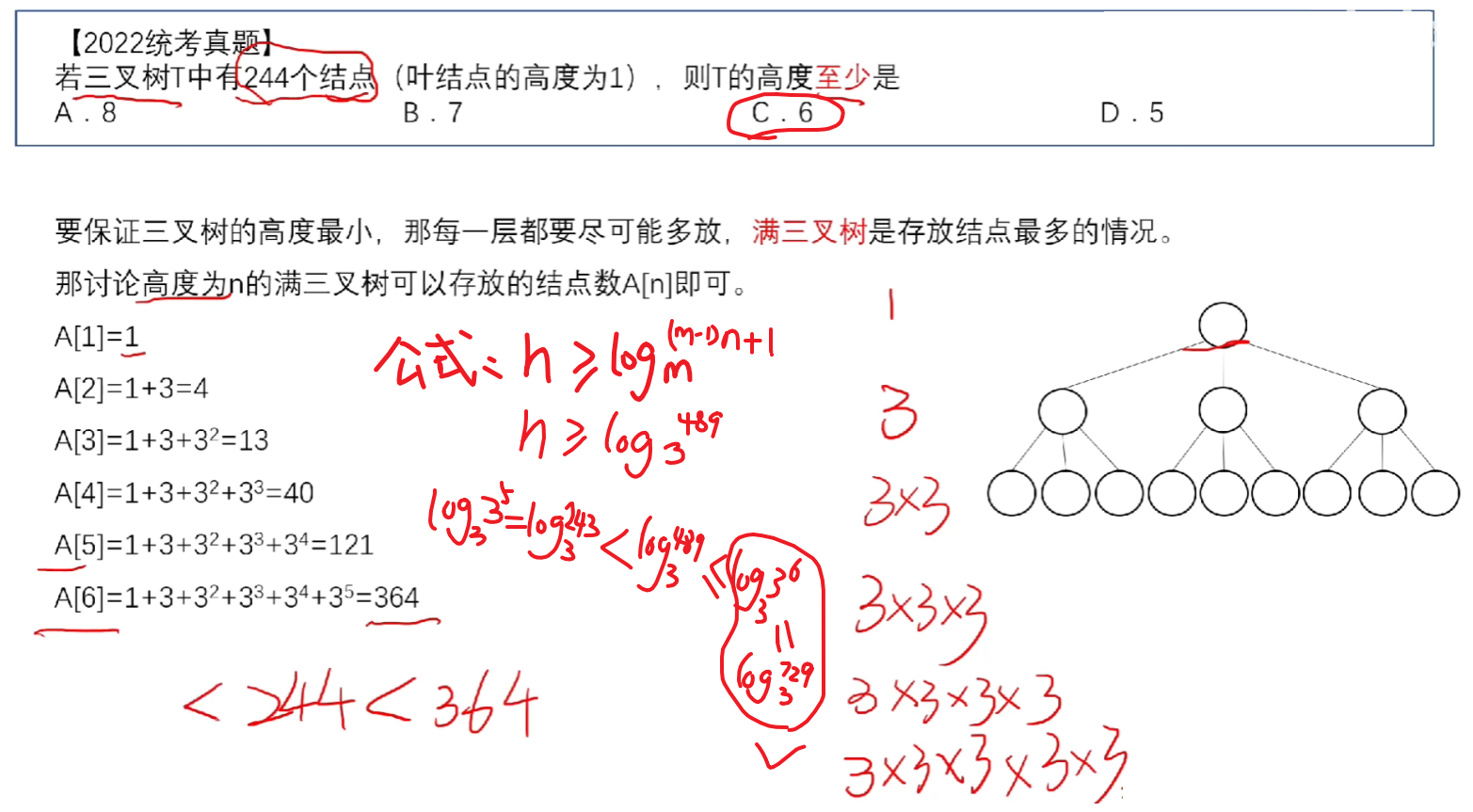
1、已知度为m、节点共n个,【最小高度h】一定一定要取到【超出
的第1个结果】,或者按照下面这个公式理解,我也不知道怎么解释反正记住就行
;
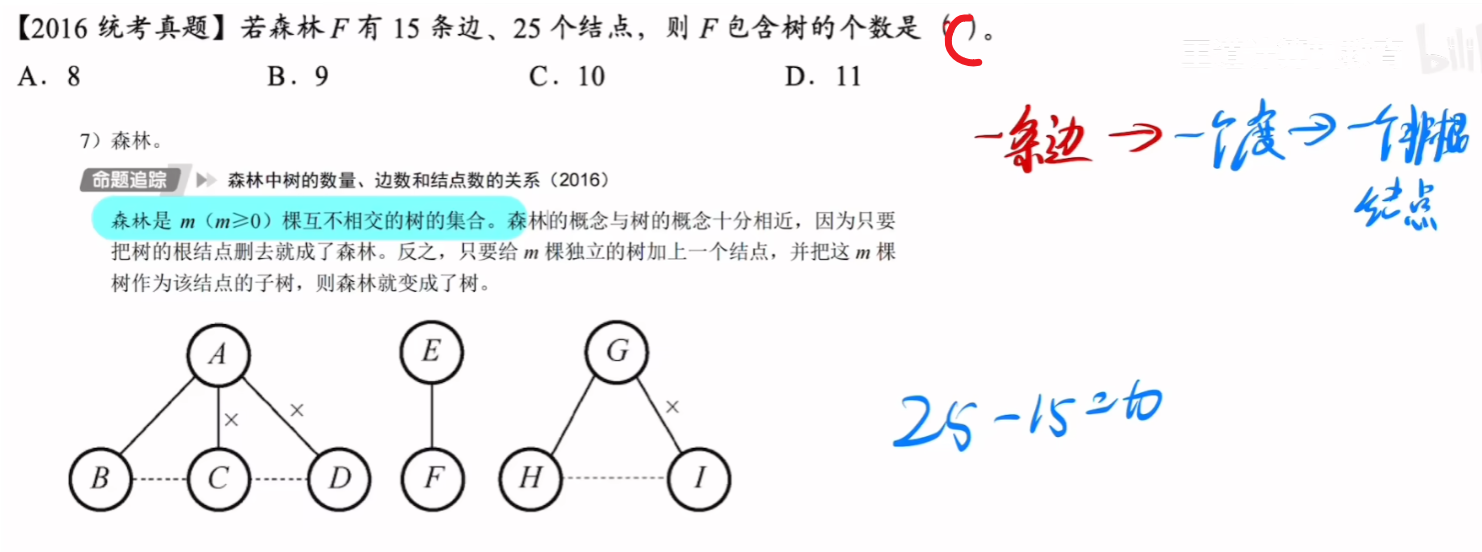
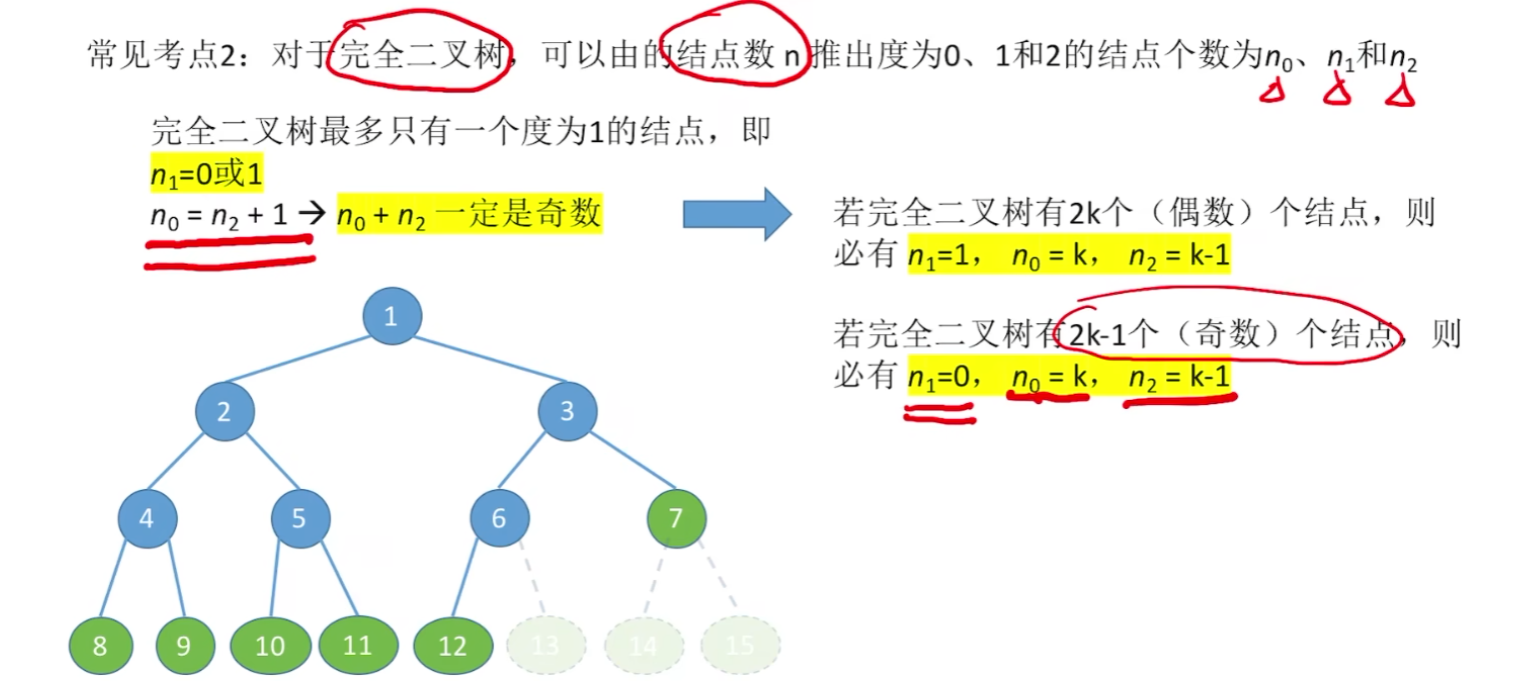
2、已知各个度数节点有几个,求总结点数的【2种平替计算公式】!!!!
4、【总结】
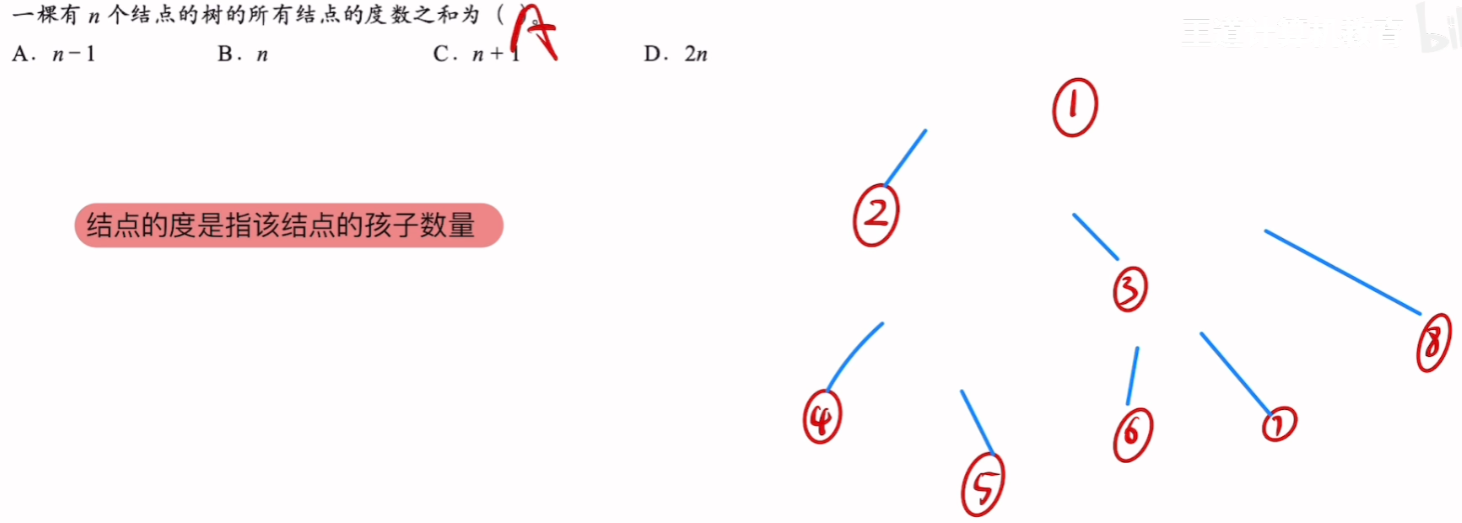
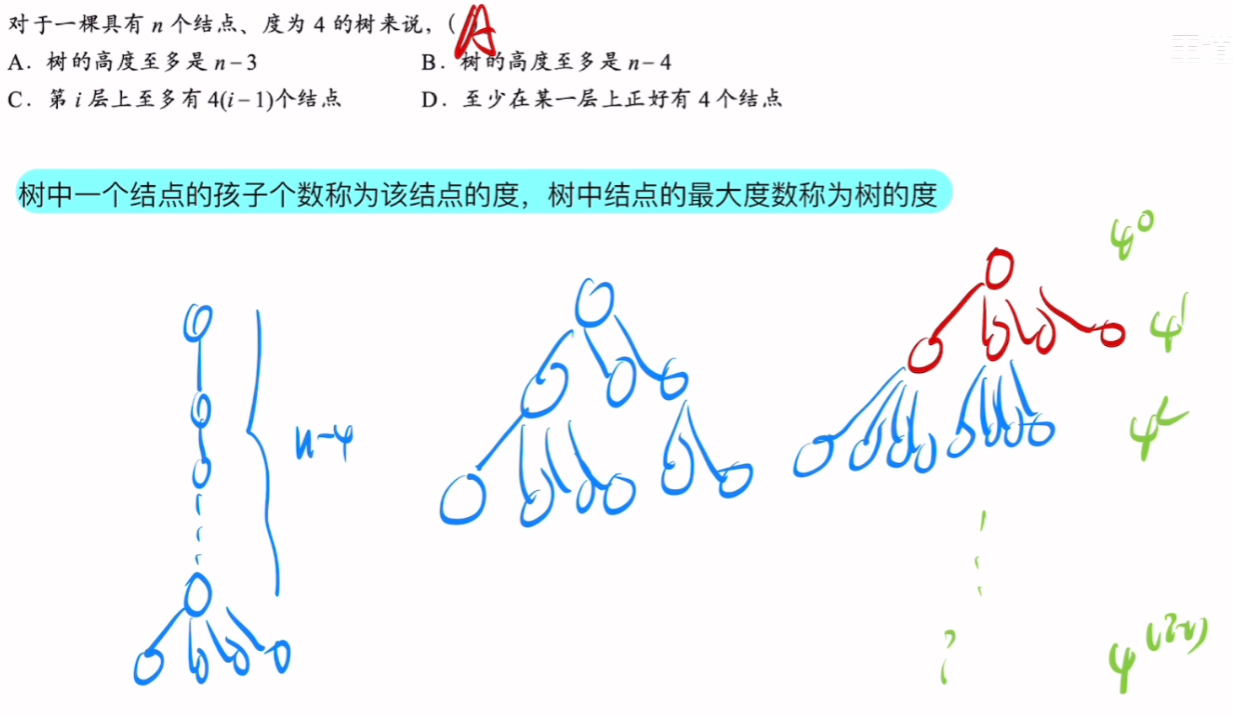
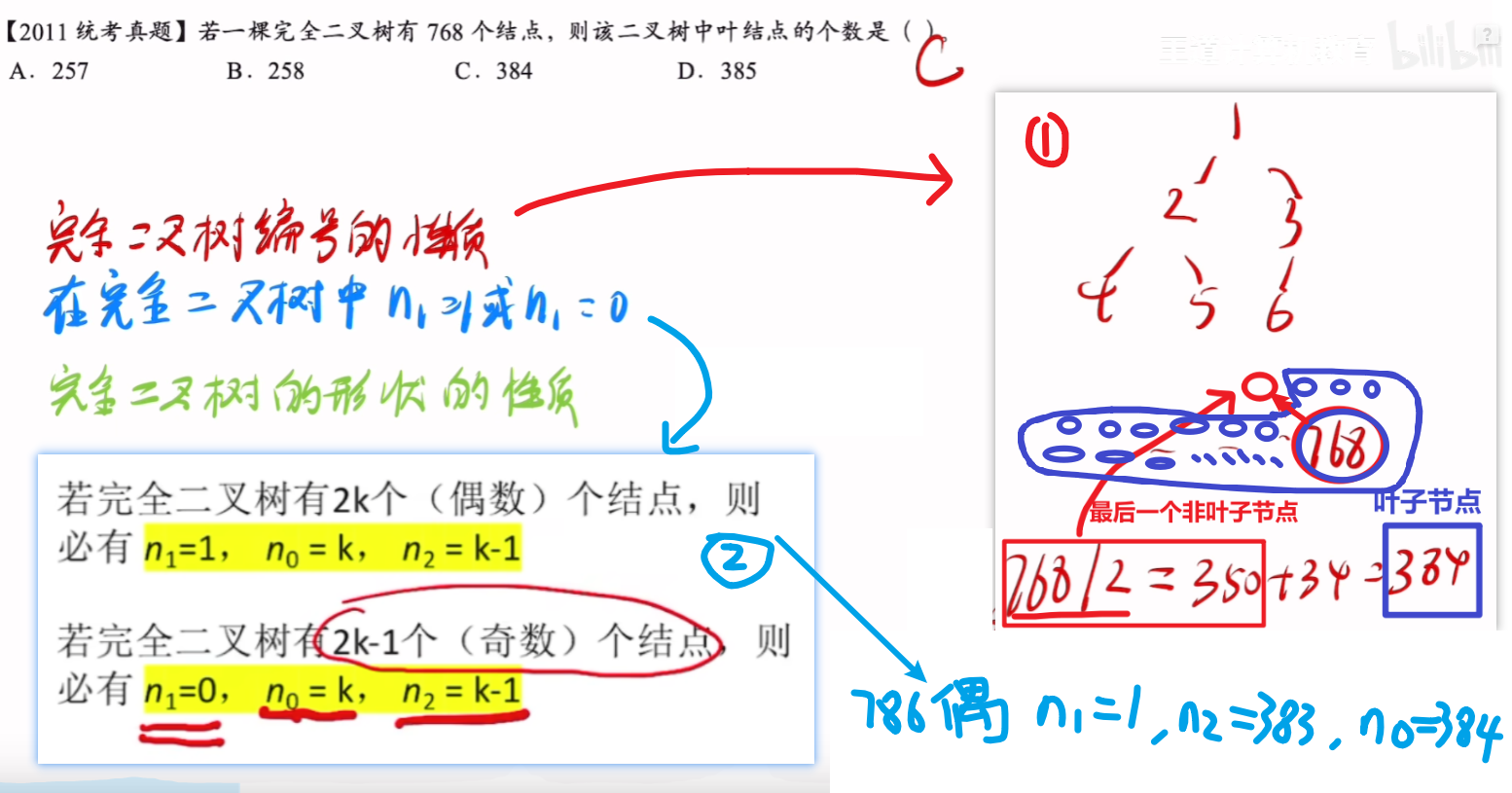
5、【例题】
二、二叉树
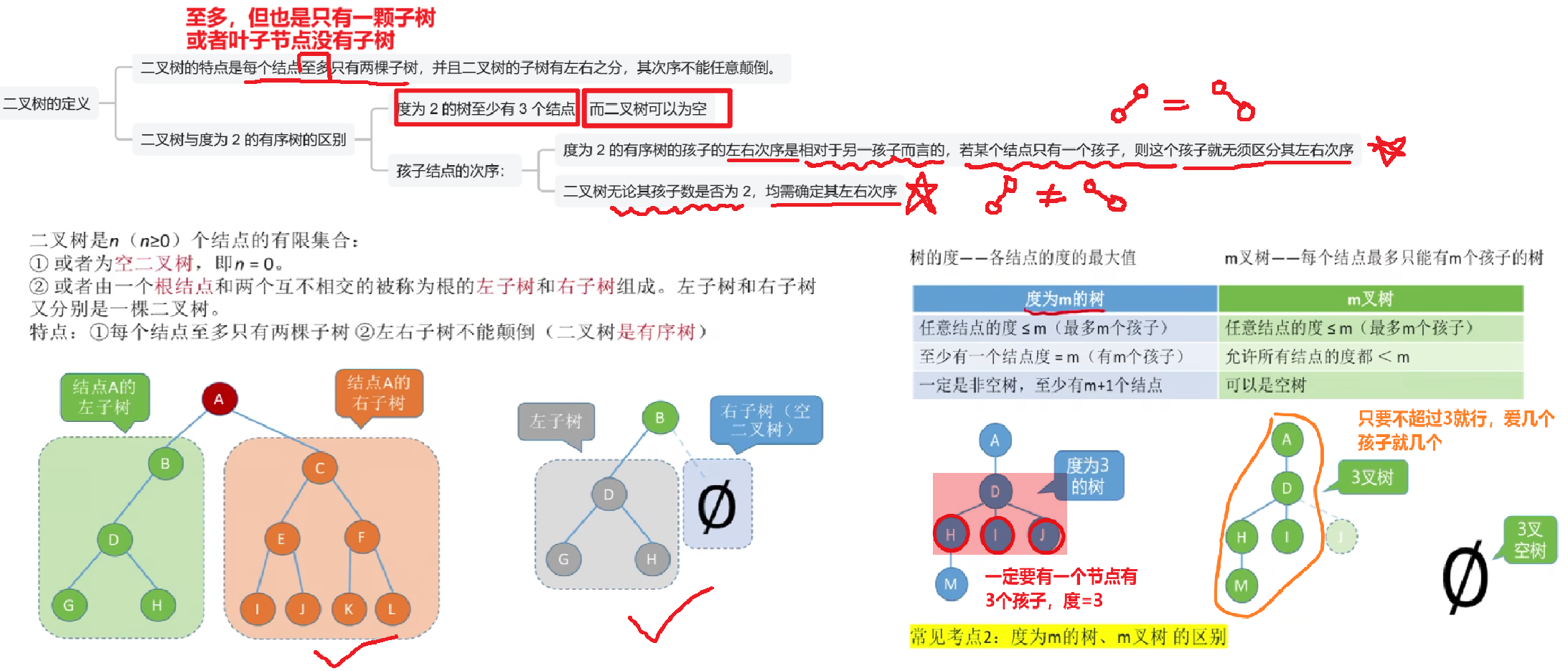
1、二叉树的定义
就是每个节点最多有【2棵子树】的树,或者说最多有【2个分支】
- 当然是【最多】,没说【一定】,【啥节点也没有的空树】也是一种【子树】
- 依旧是狗屎图,需要各位放大,不过也没什么知识点,只是要注意区分一下【二叉树】和【度为2的树】二者的区别
2、特殊二叉树
这个思维导图我就不乱画了,先仔细回忆一下
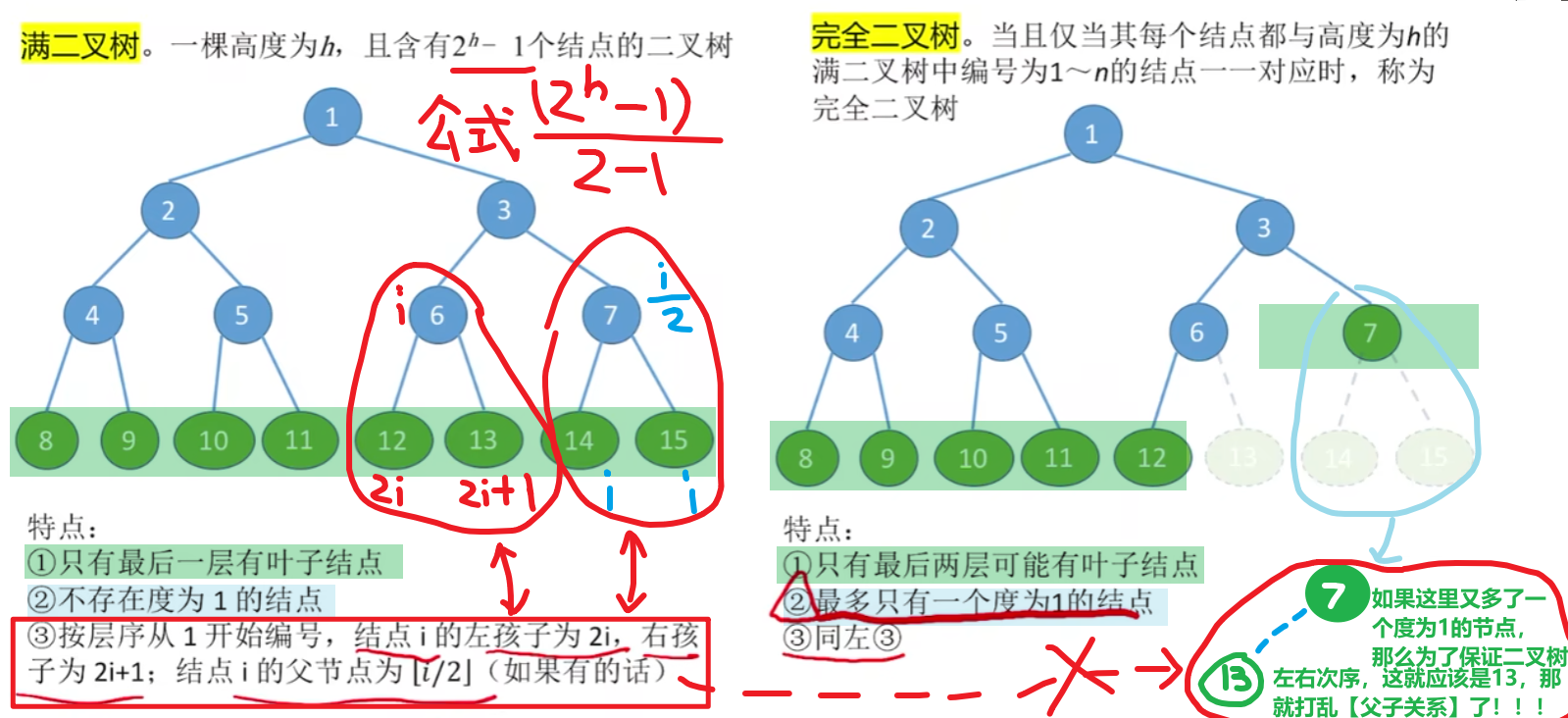
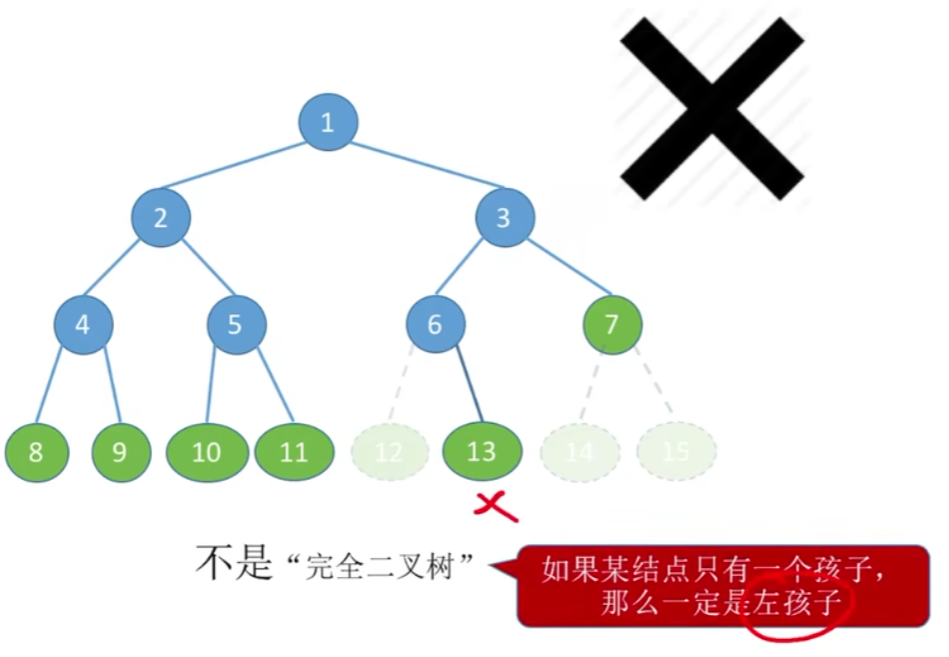
1)【满二叉树】和【完全二叉树】
【满二叉树】一定是【完全二叉树】,但是【完全二叉树】不一定是【满二叉树】
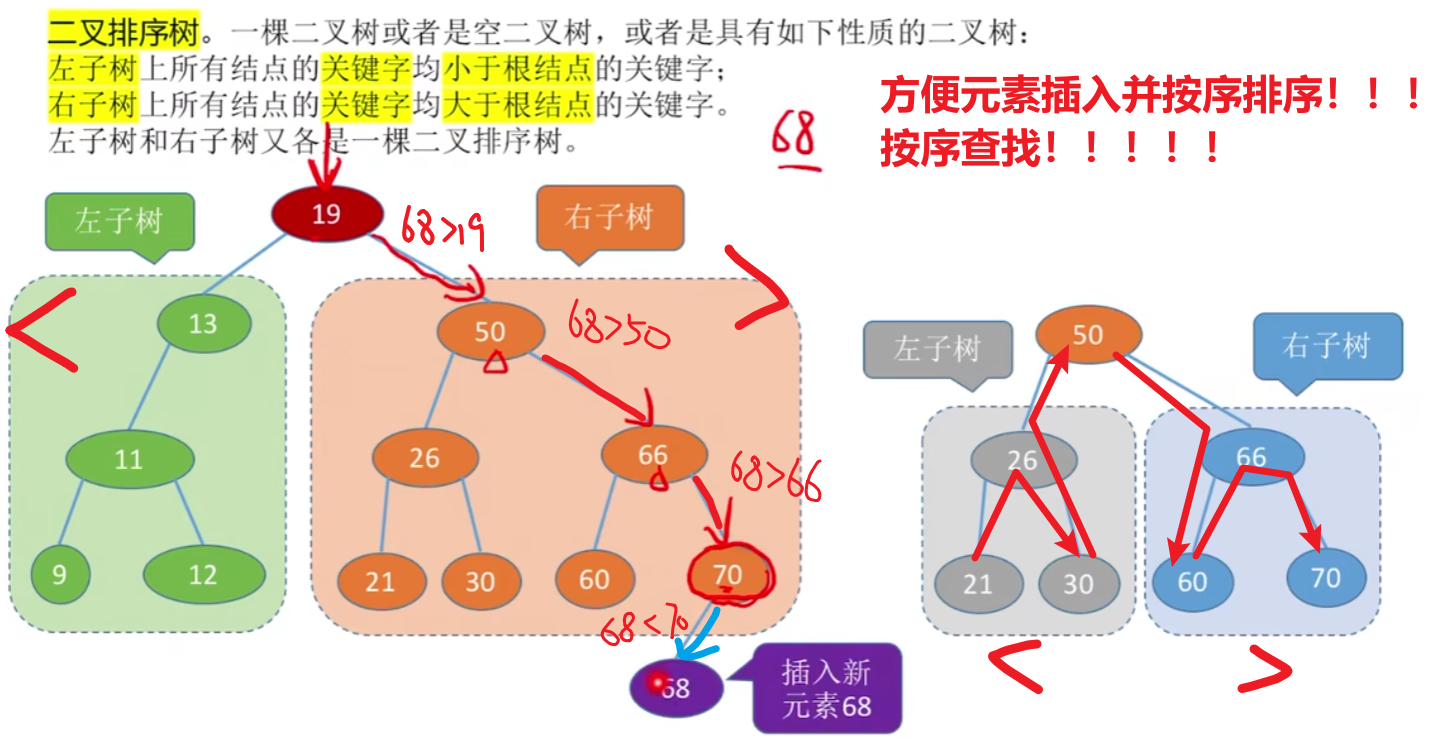
2)二叉排序树
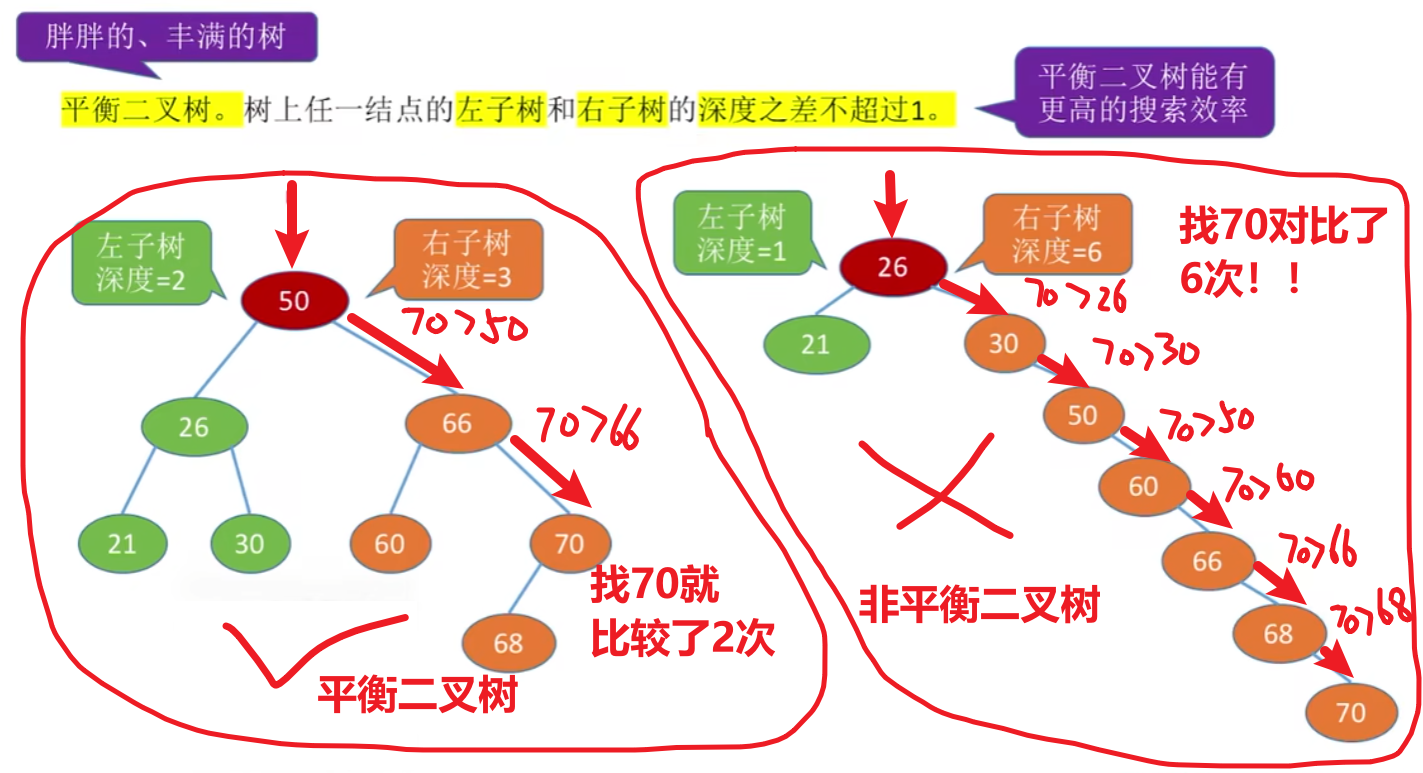
3)平衡二叉树
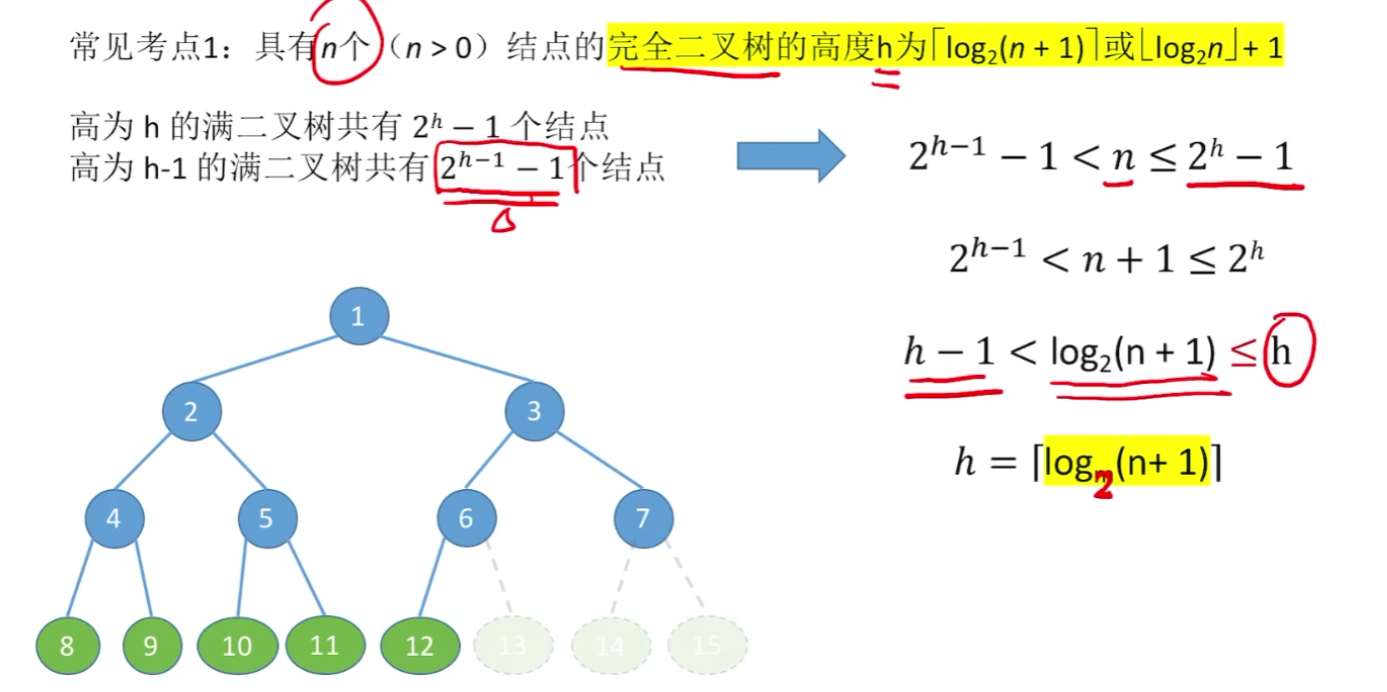
3、二叉树的性质
;
;
我懒得打字解释了,全部都可以按前面【树的性质】推算,只要牢记【二叉树的度<=2】就行了(一般按度数m=2计算就可以了)
;
【留意一下:完全二叉树】
【例题】
4、二叉树的存储结构(感觉出的题很少,应该非重点)
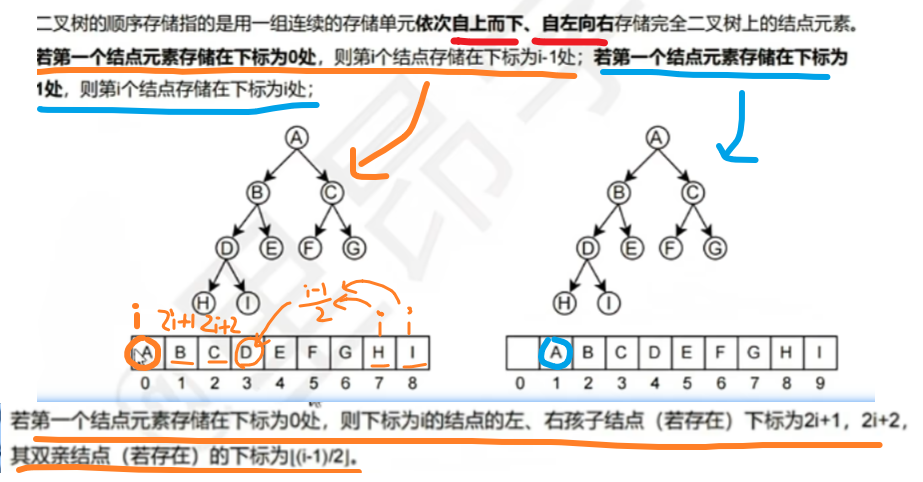
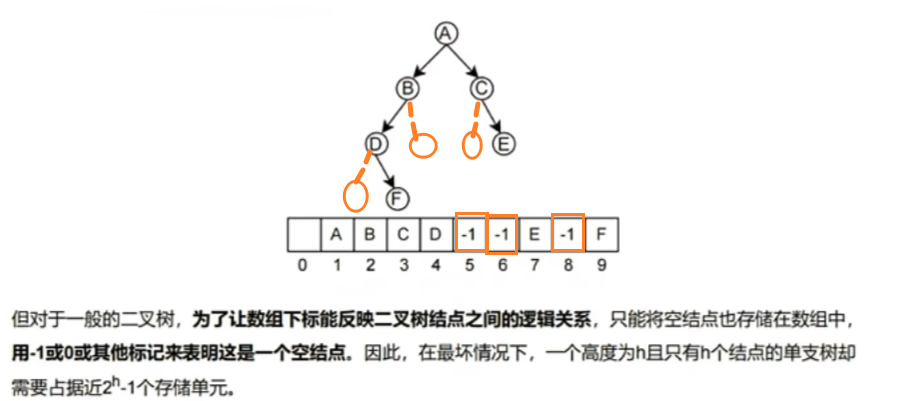
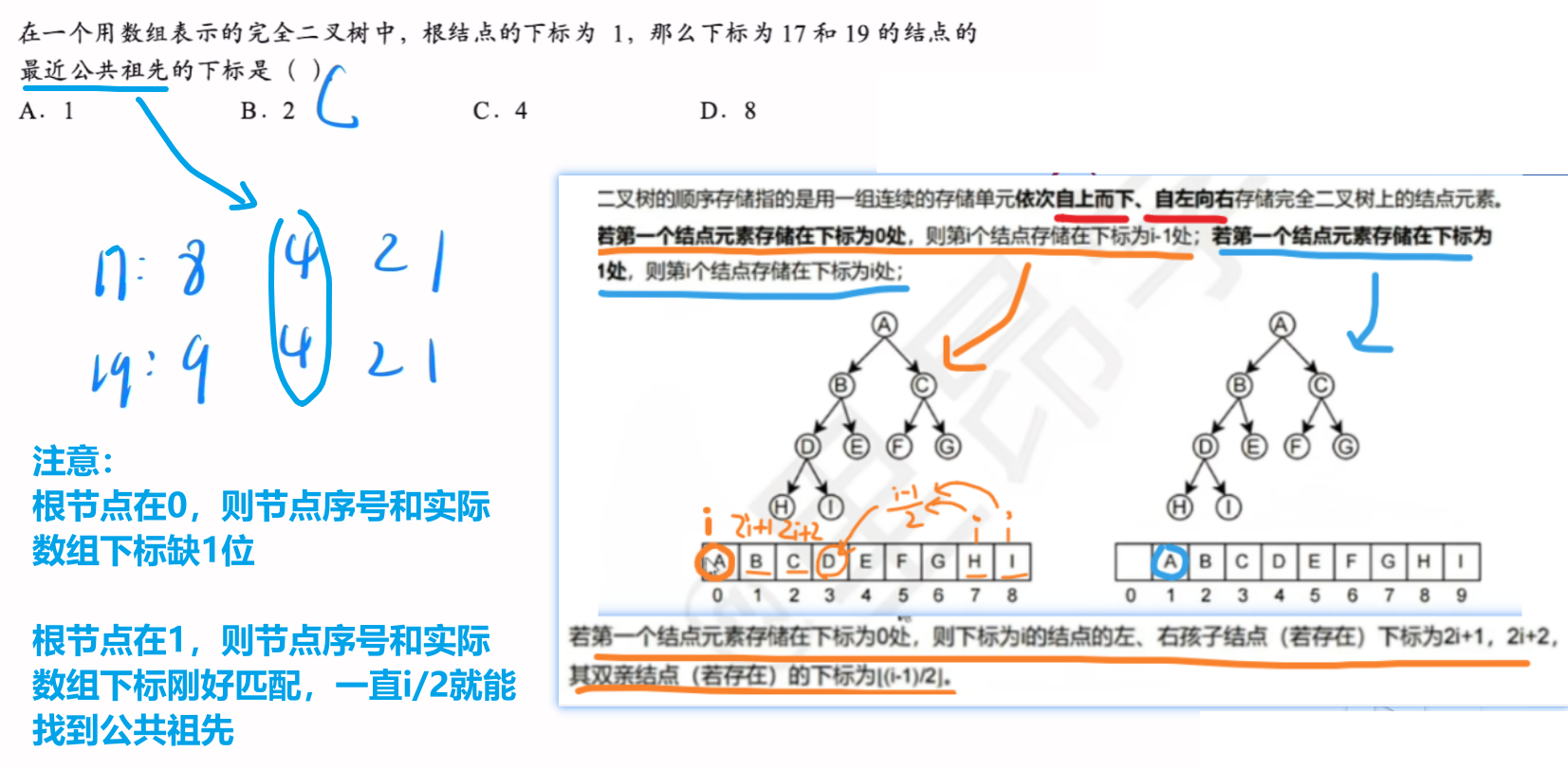
1)第一种:顺序存储
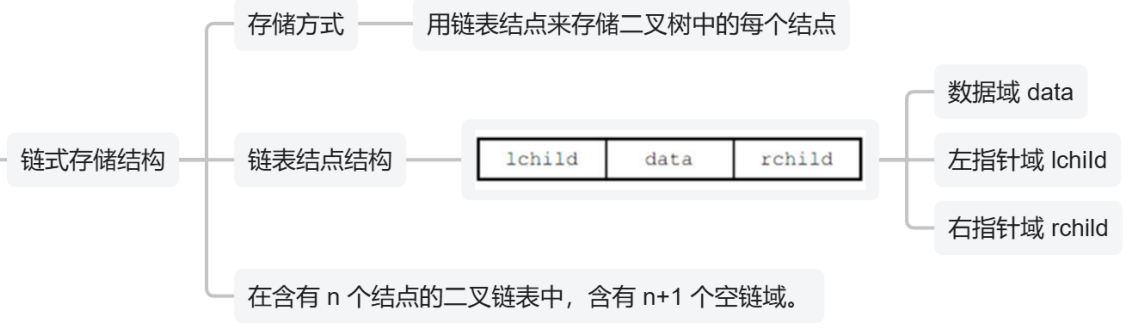
2)第二种:链式存储
;
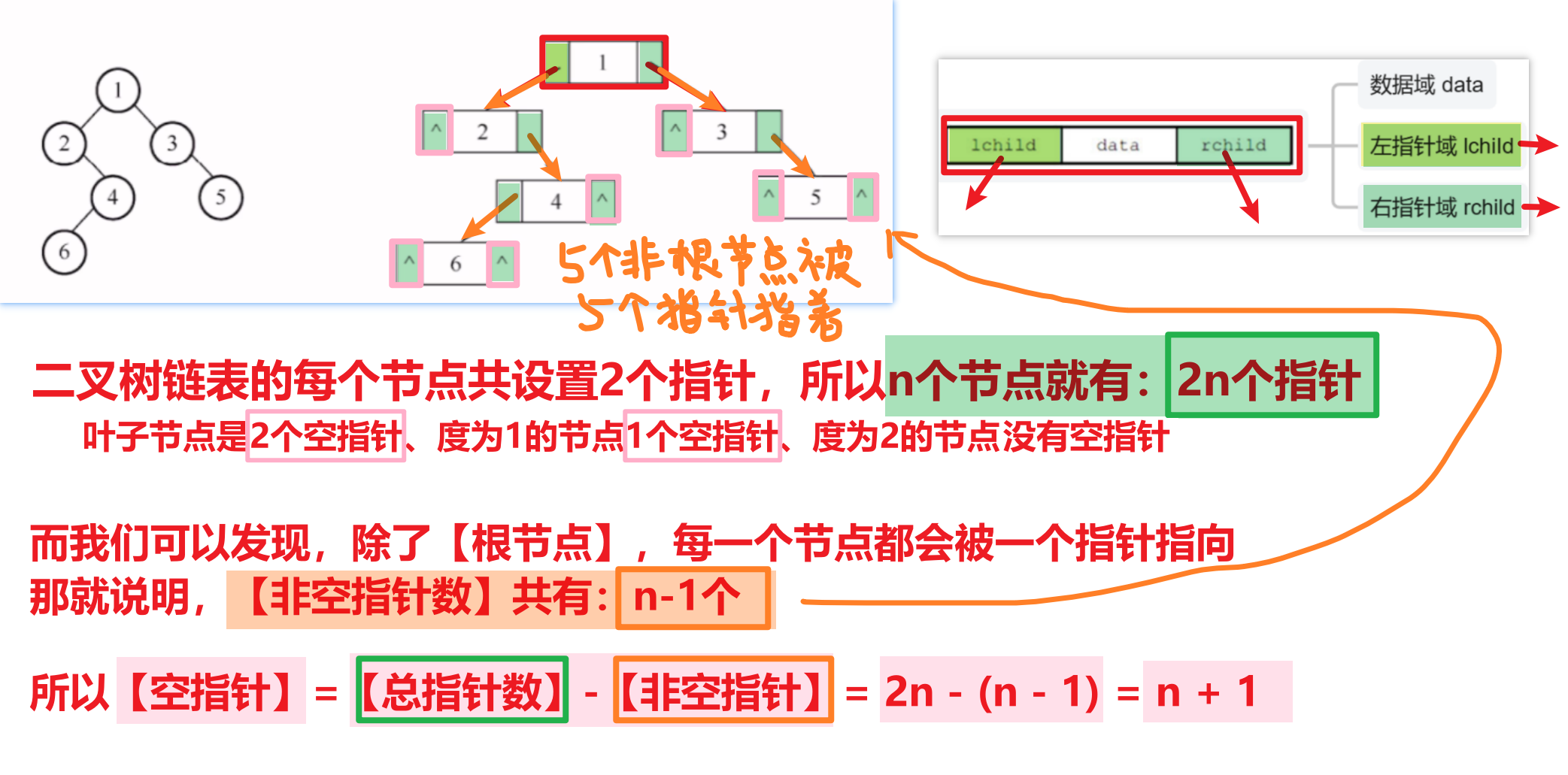
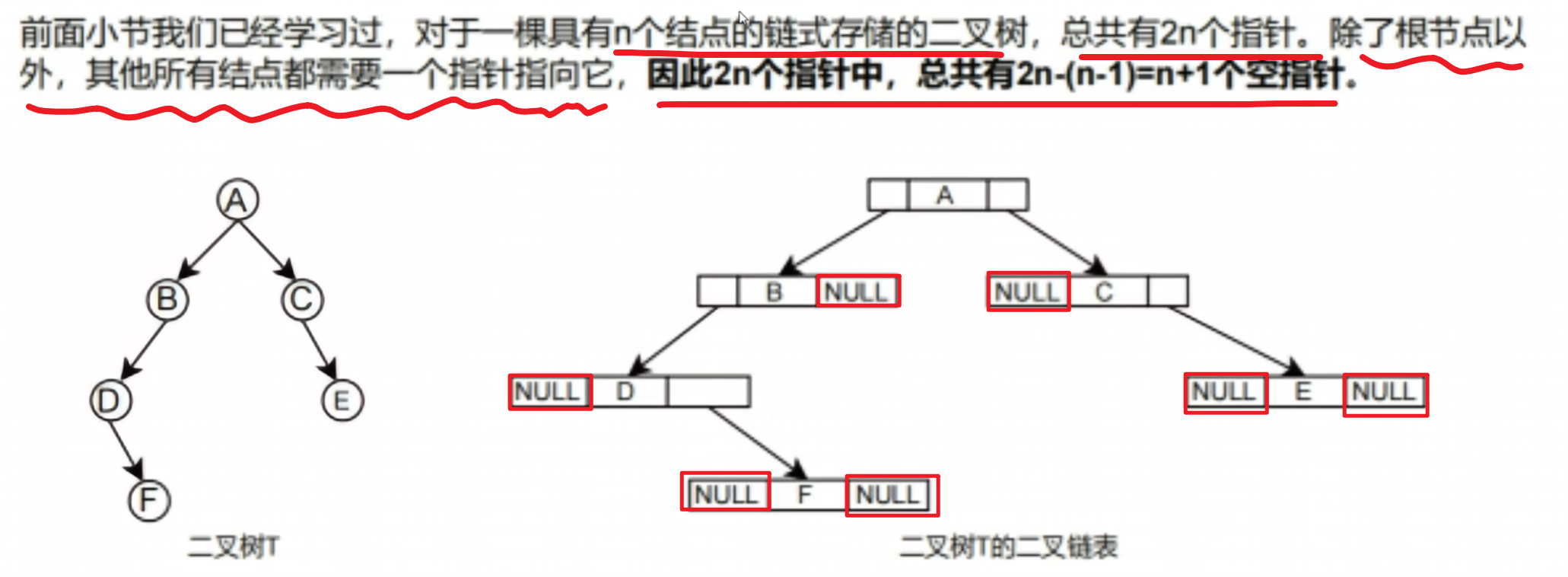
【注意考点!!】
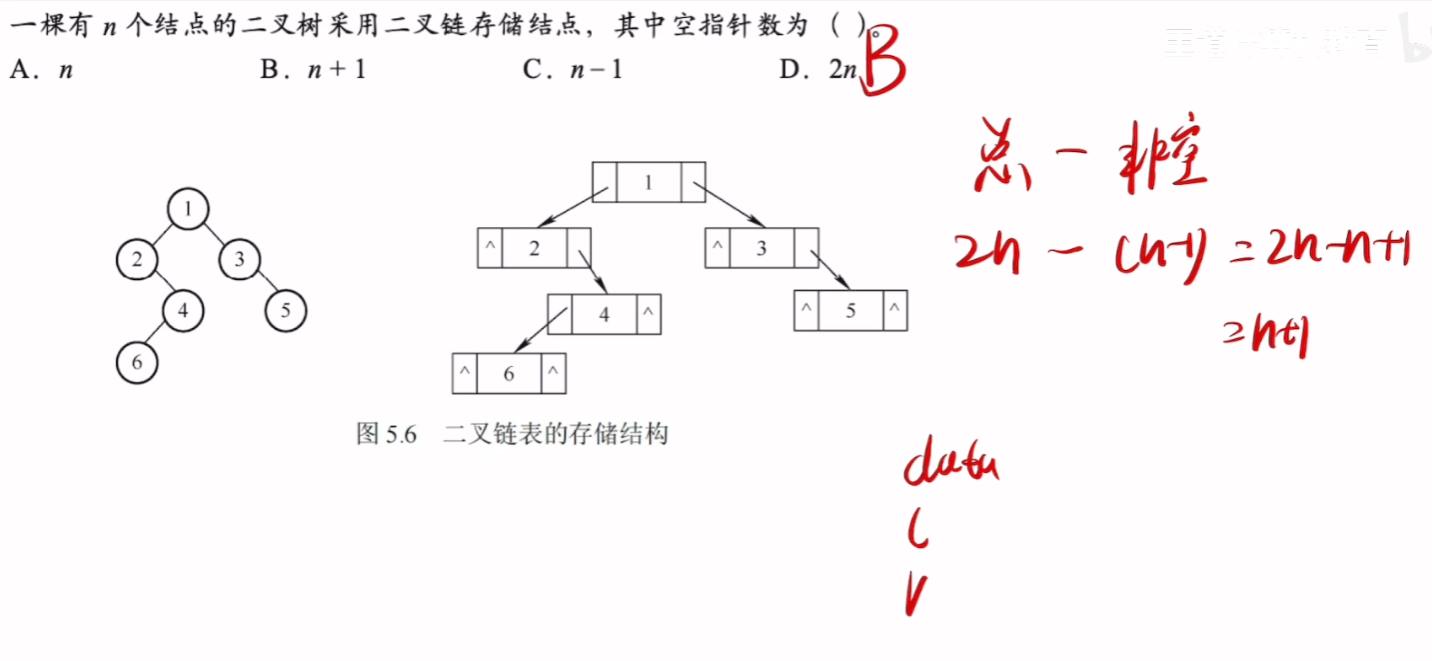
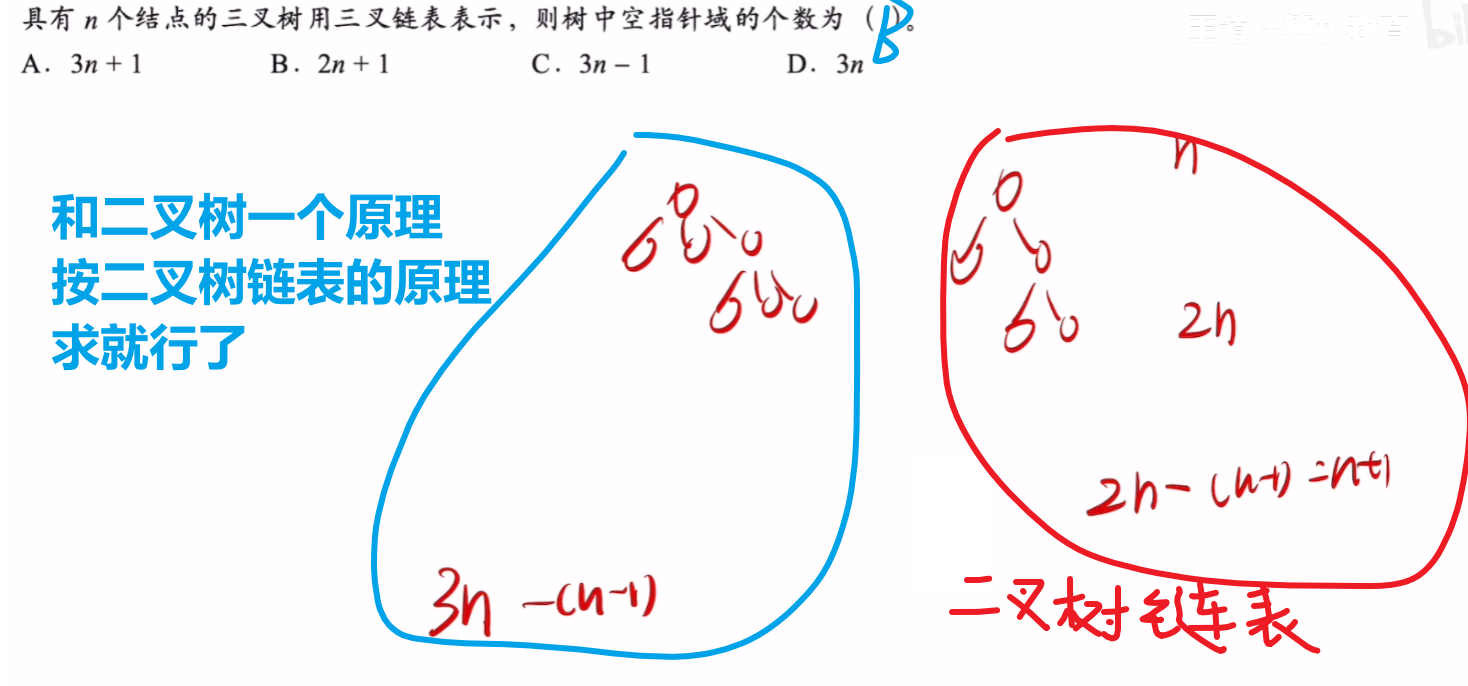
- 【二叉树二指针】情况的【指针数】
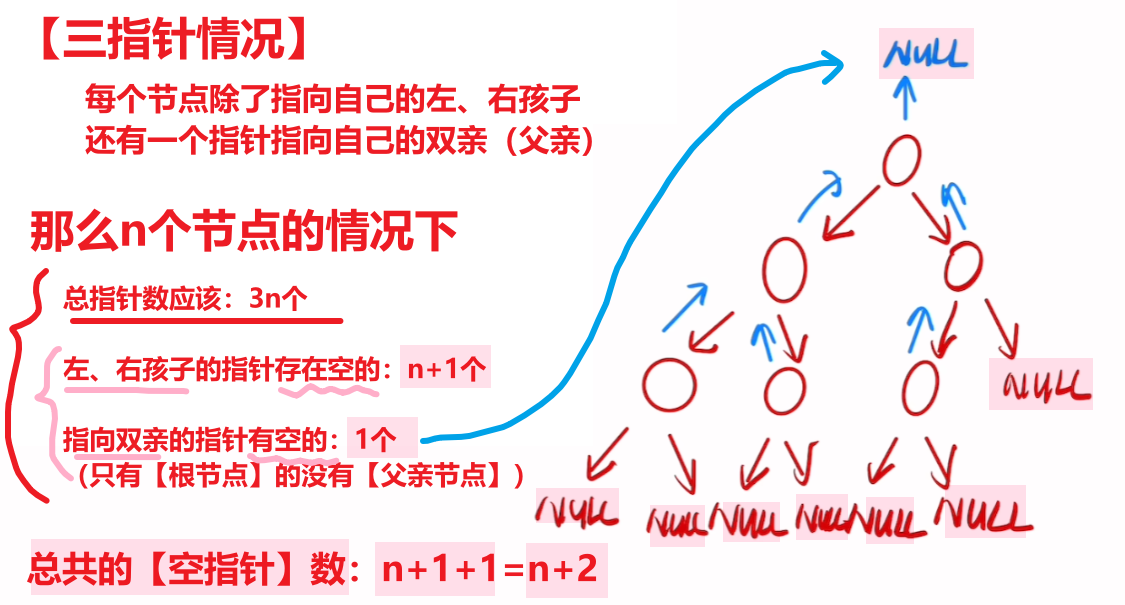
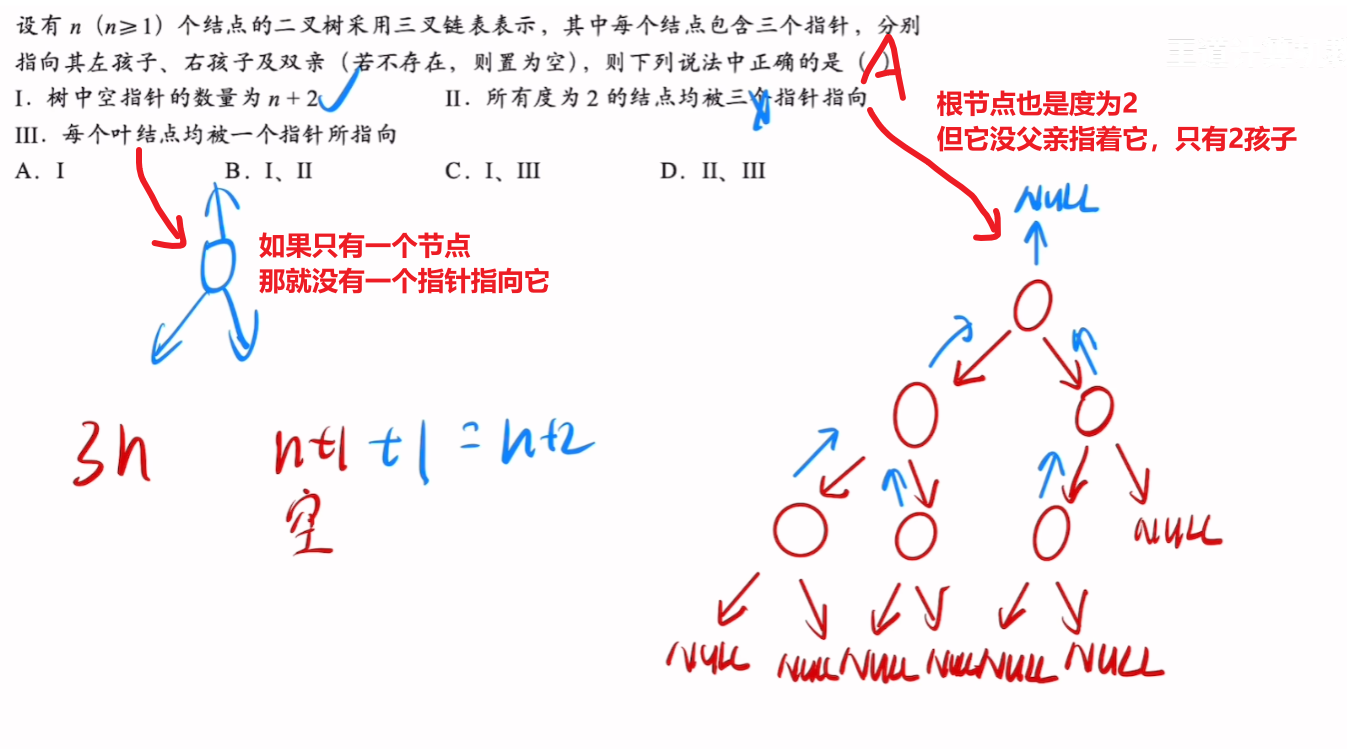
- 【二叉树三指针】情况的【指针数】
【例题】
5、二叉树的遍历(常考)
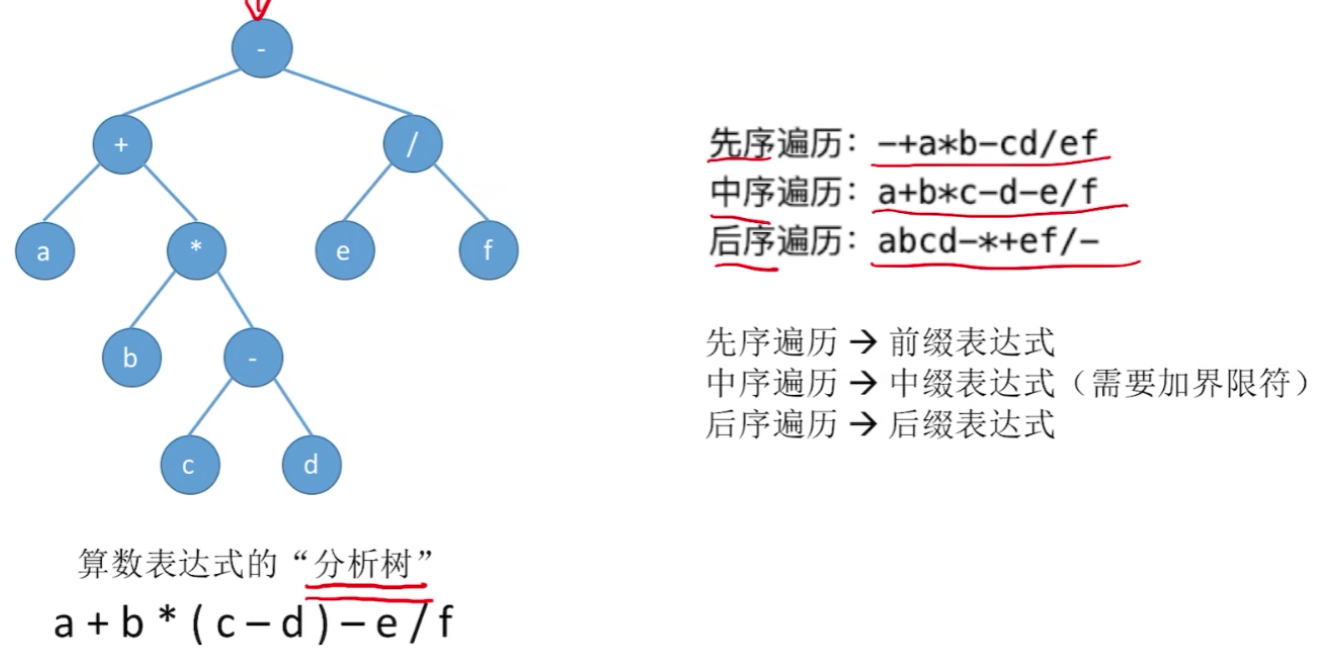
【三大类遍历的总结】
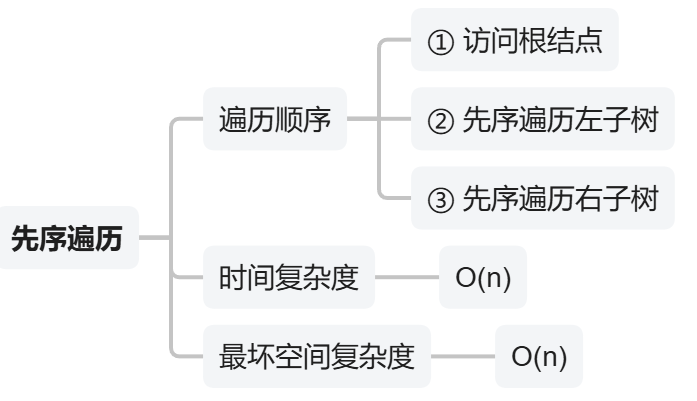
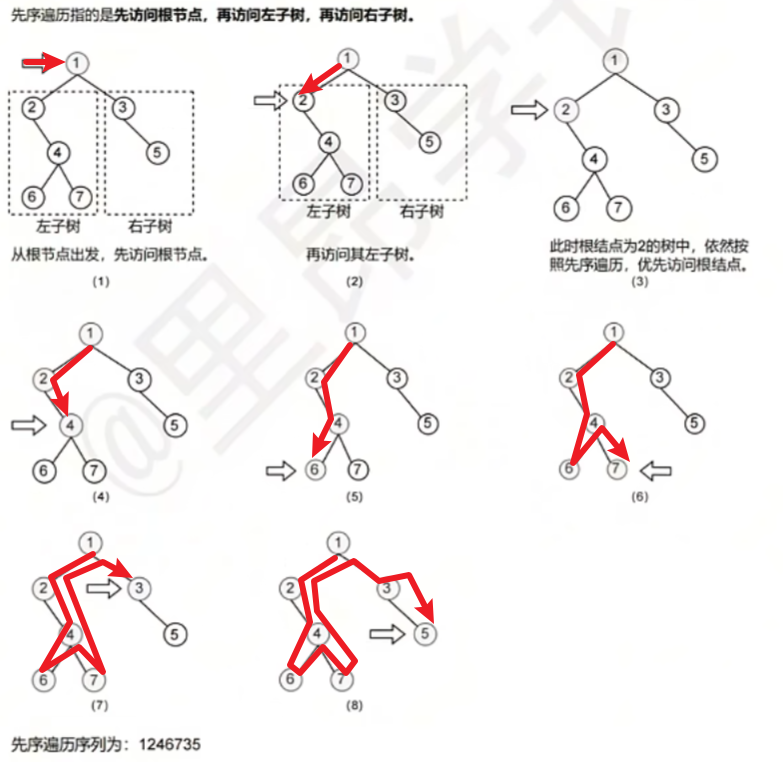
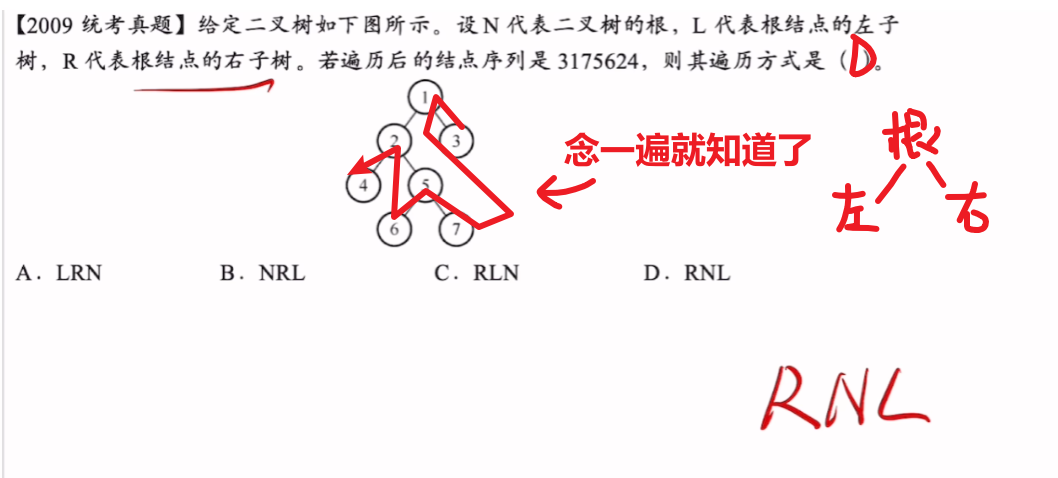
1)先序遍历【根左右】
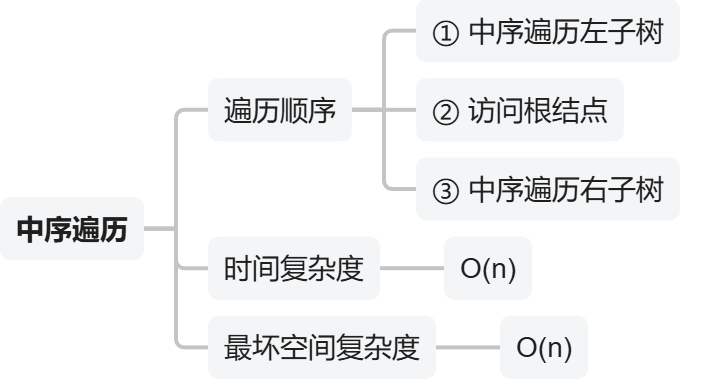
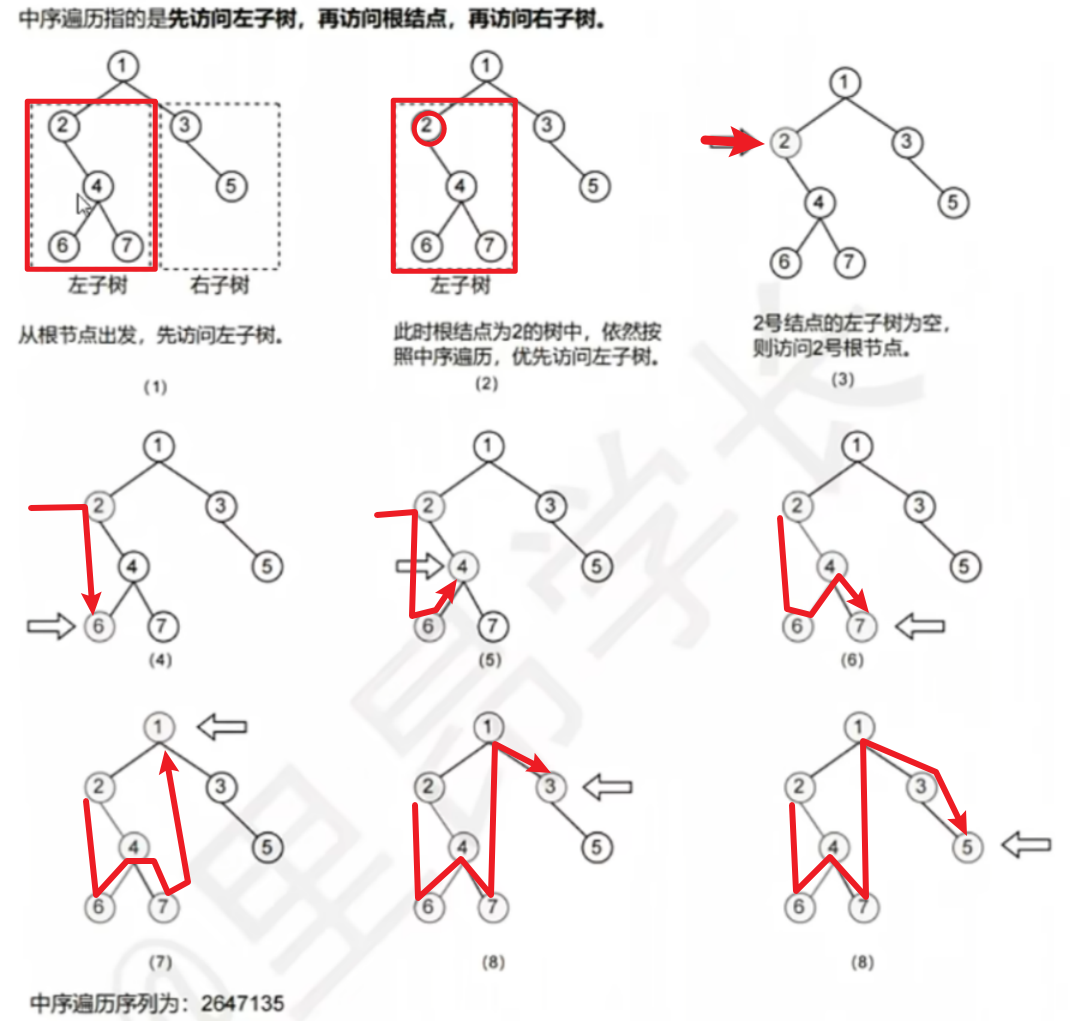
2)中序遍历【左根右】
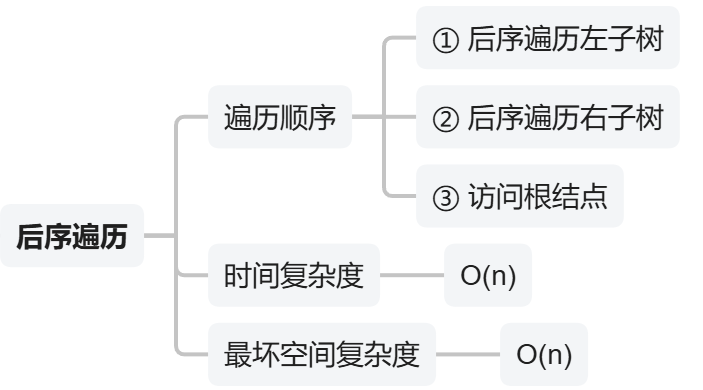
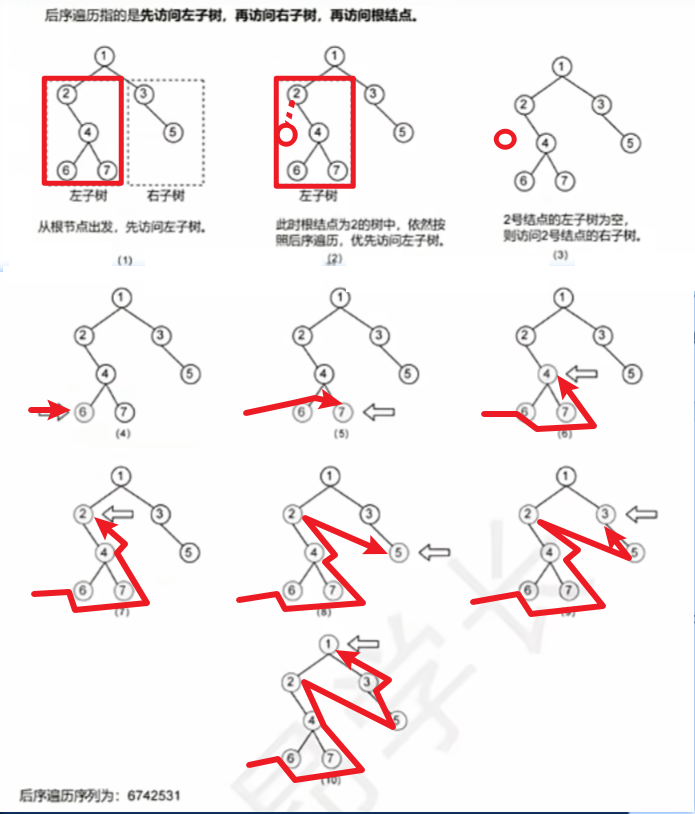
3)后序遍历【左右根】
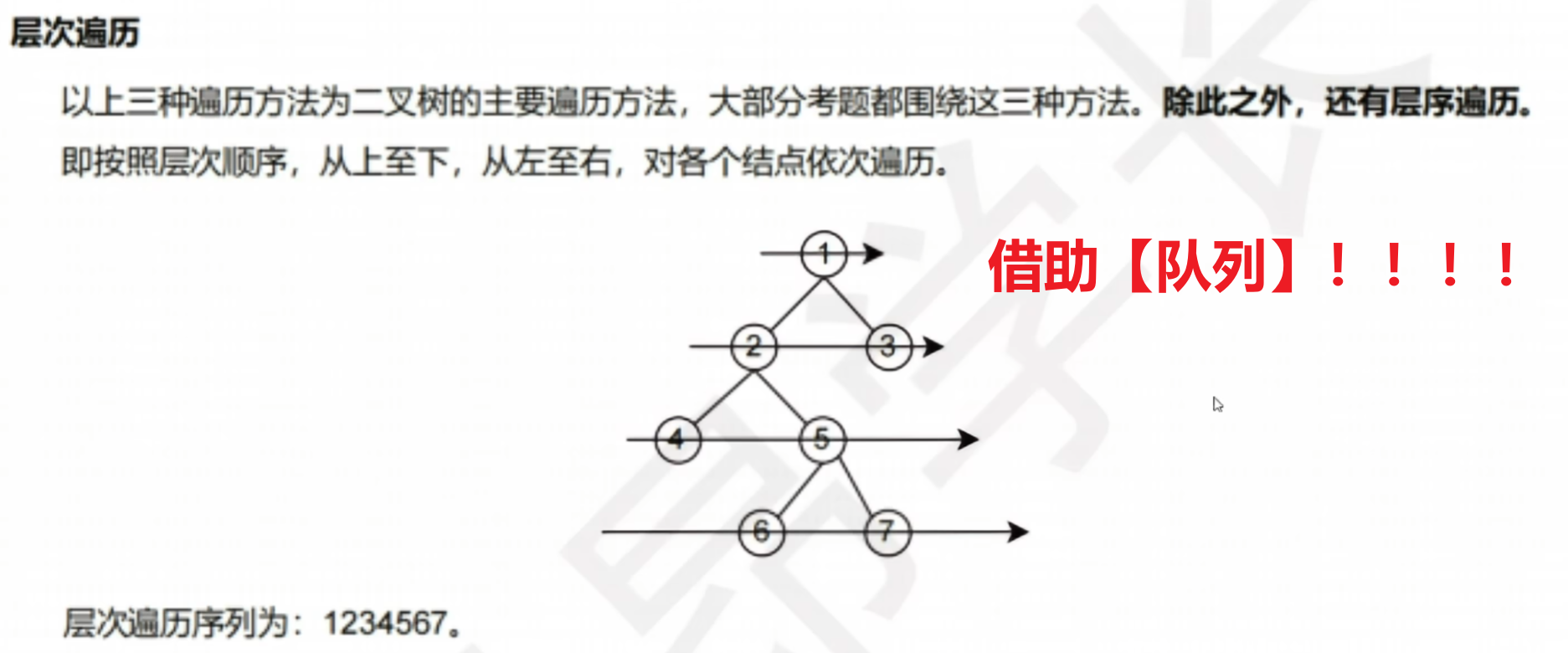
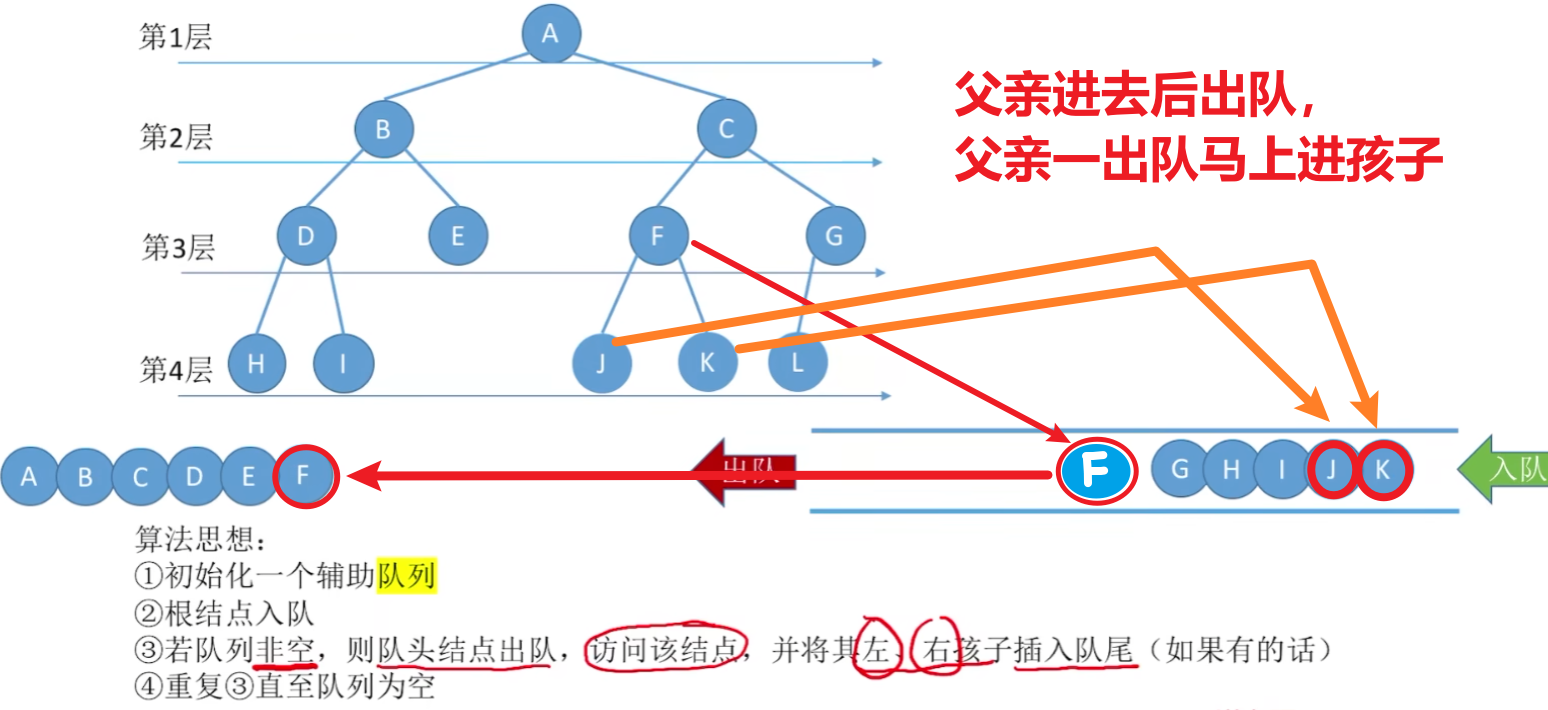
4)层次遍历
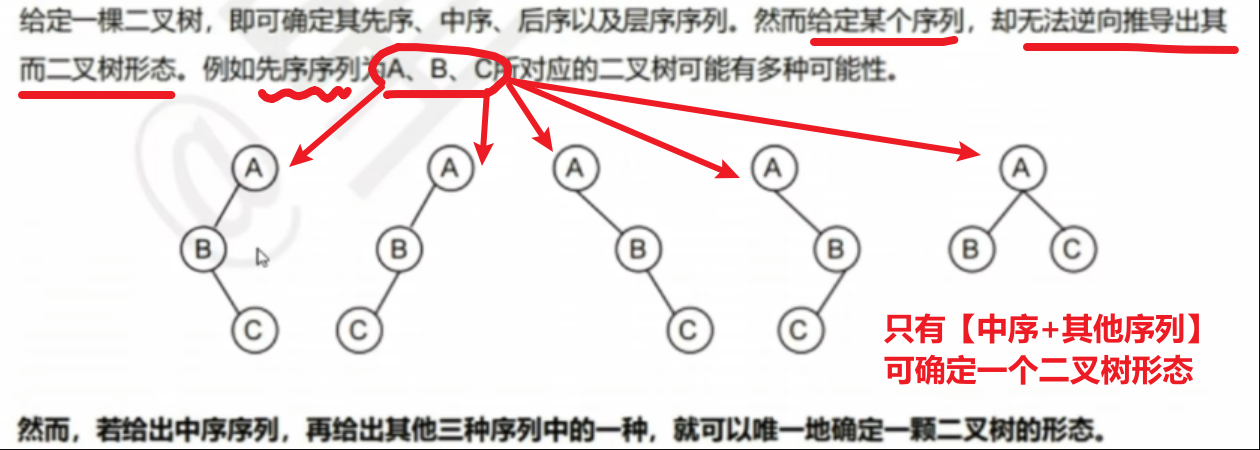
5)由遍历序列构造二叉树
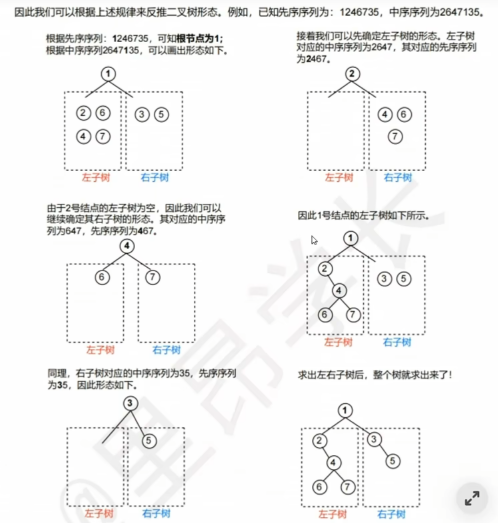
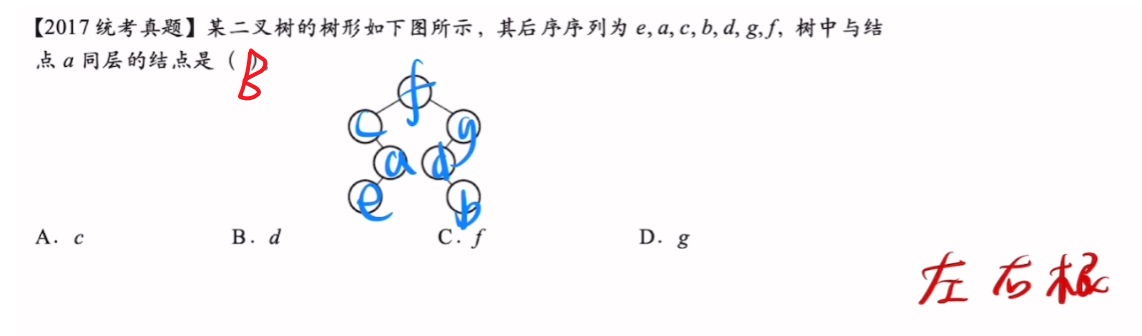
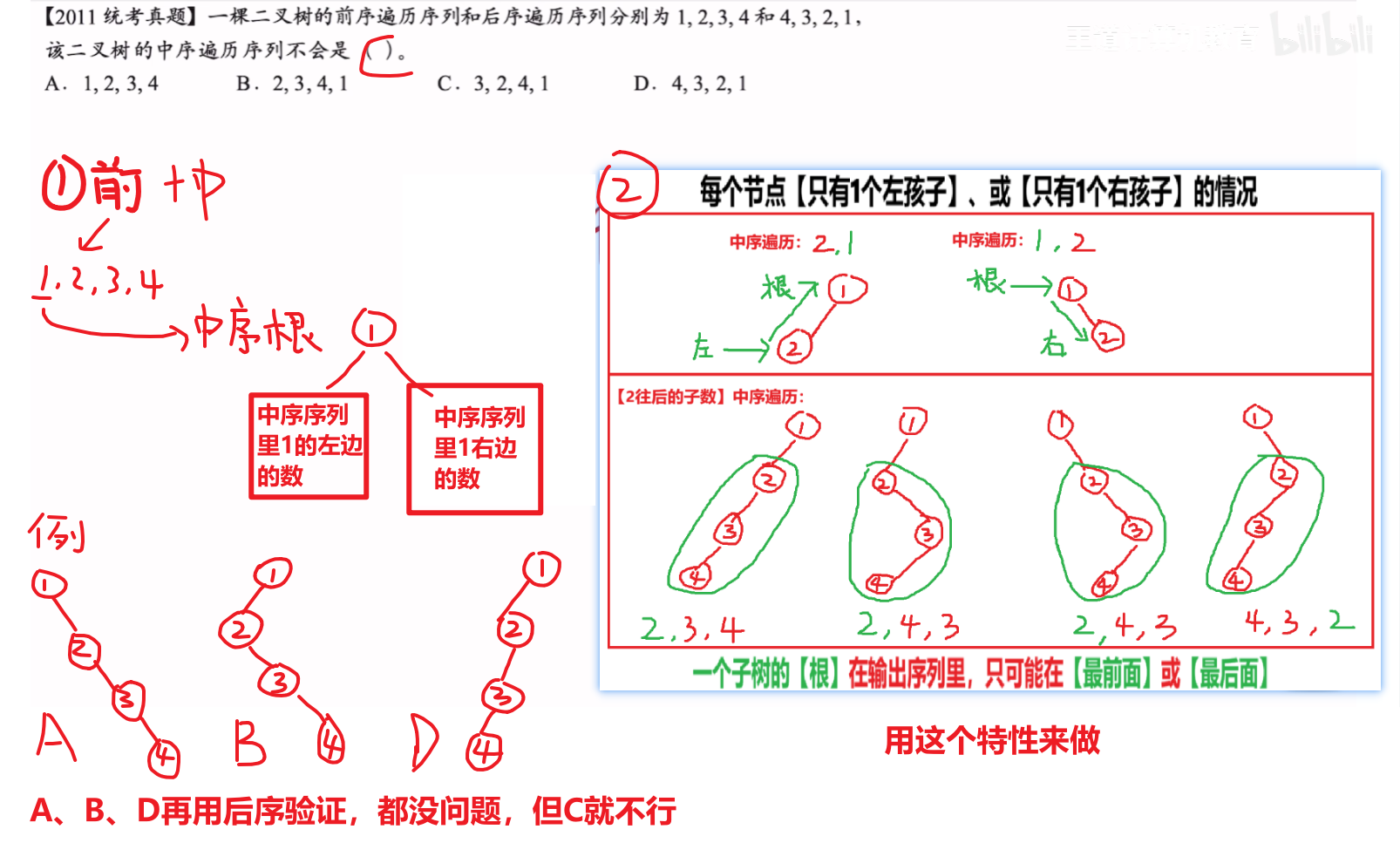
【先序 + 后序】
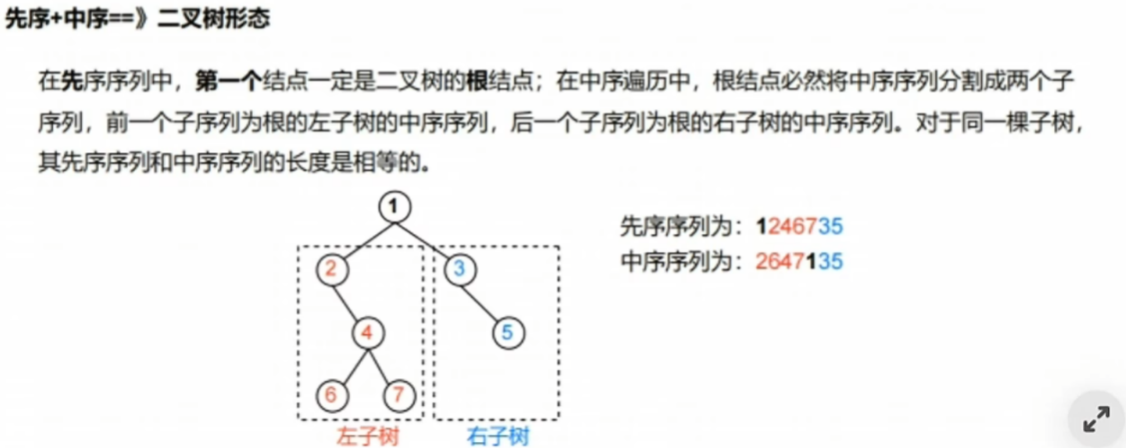
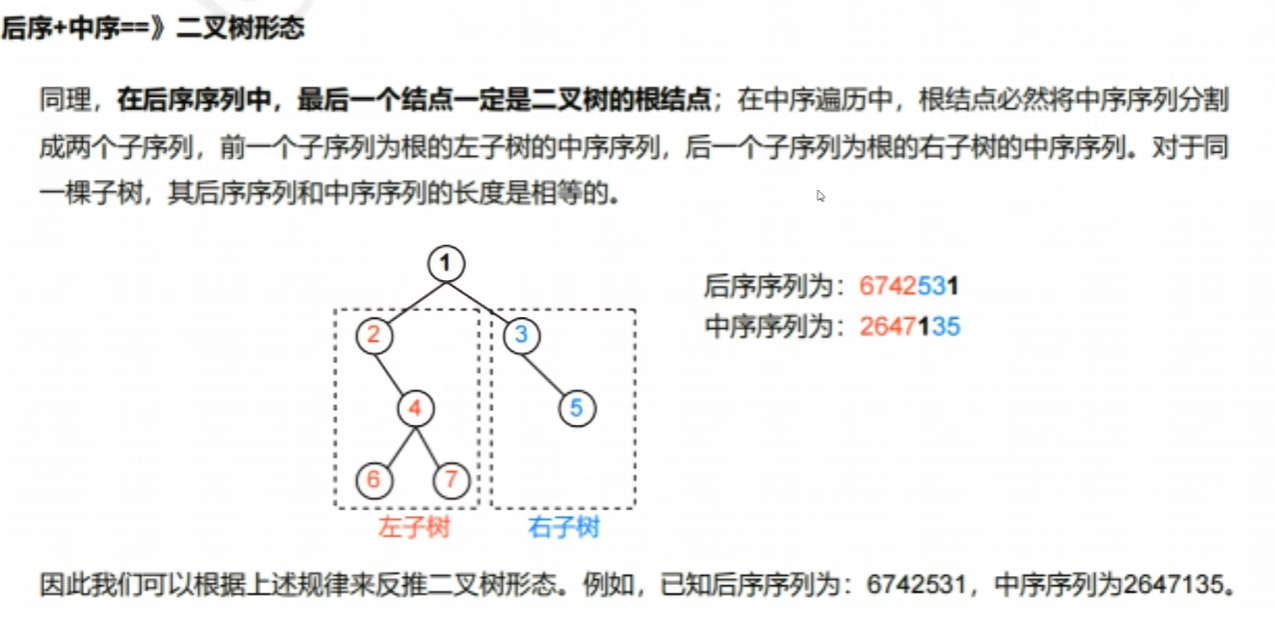
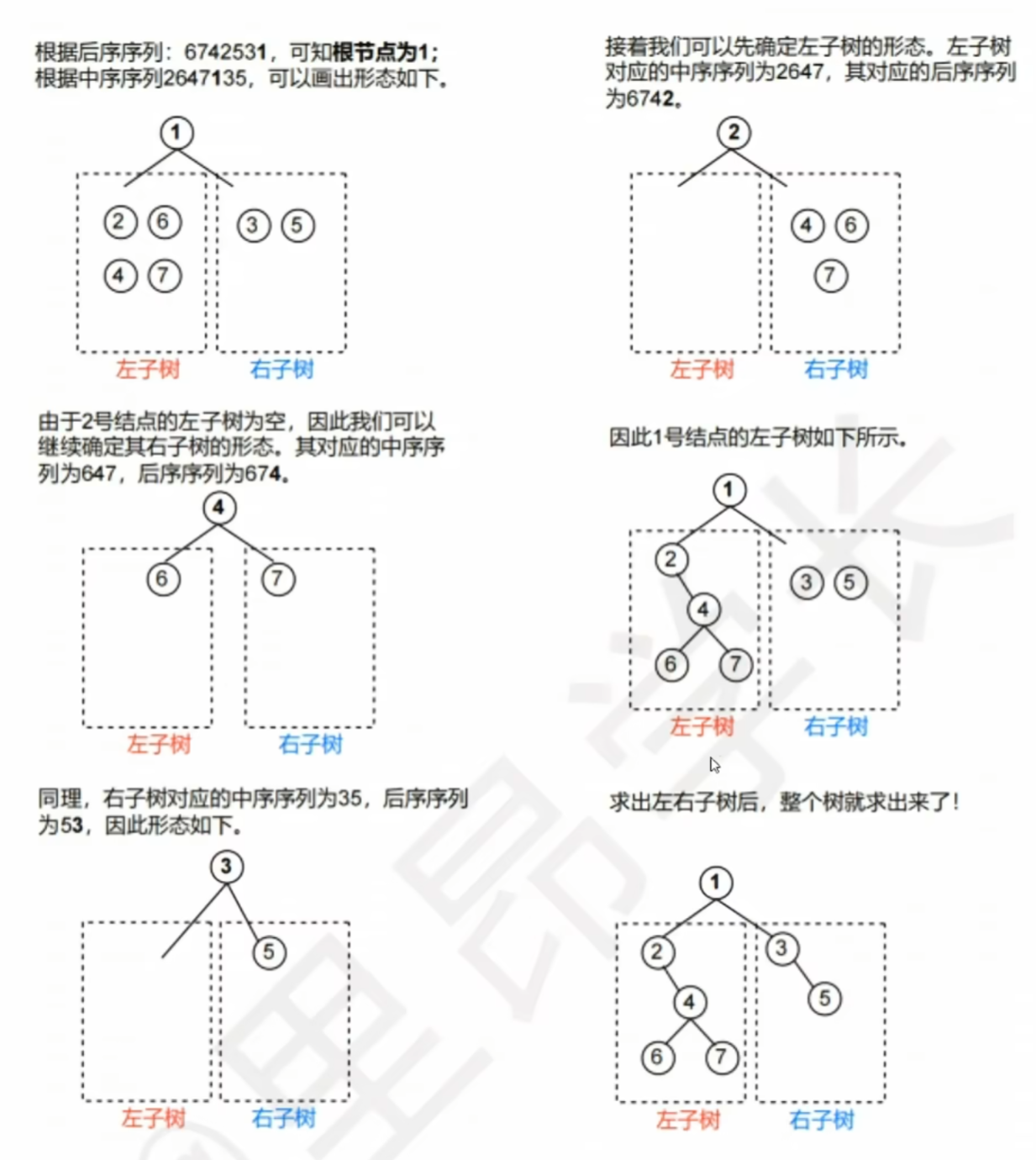
【后序+中序】
;
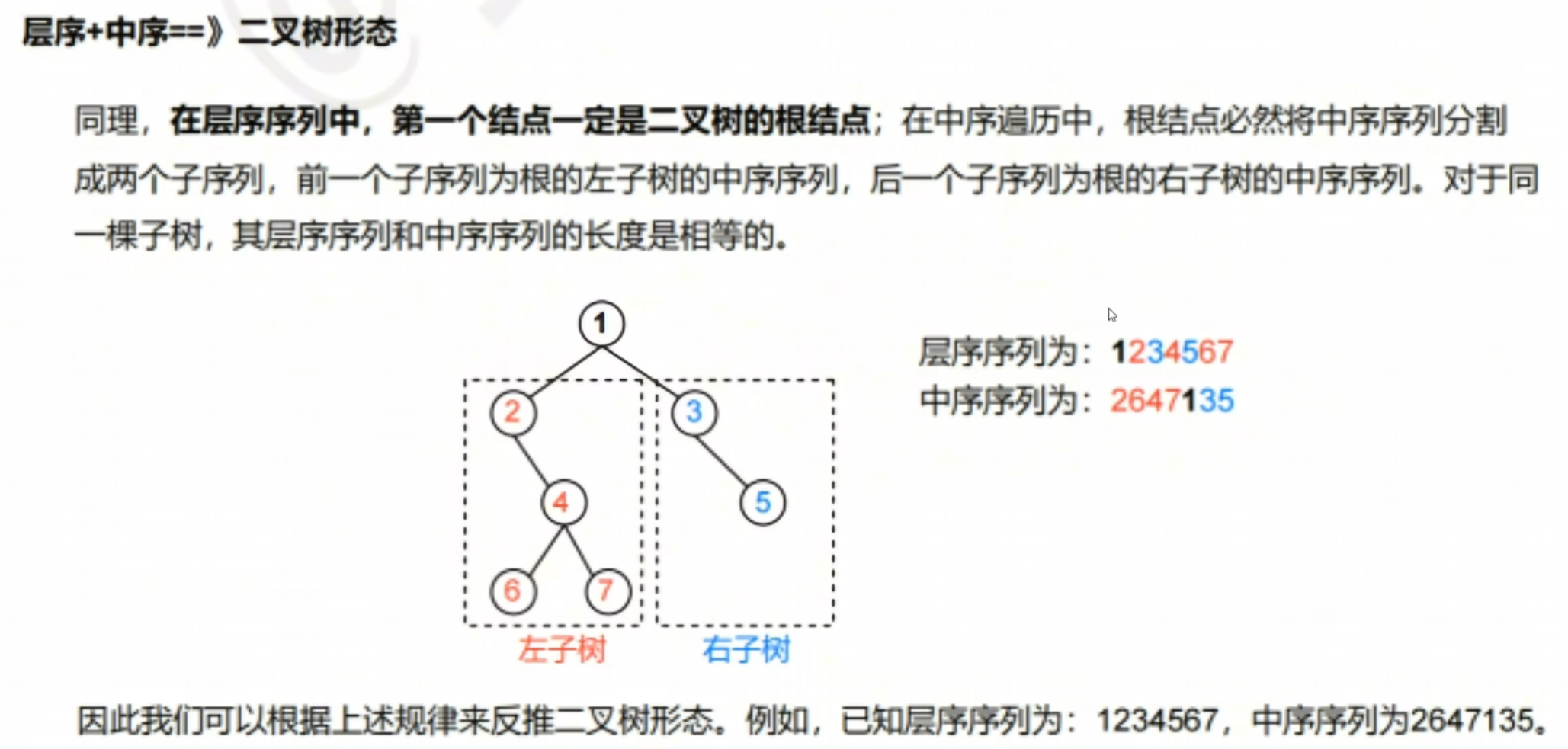
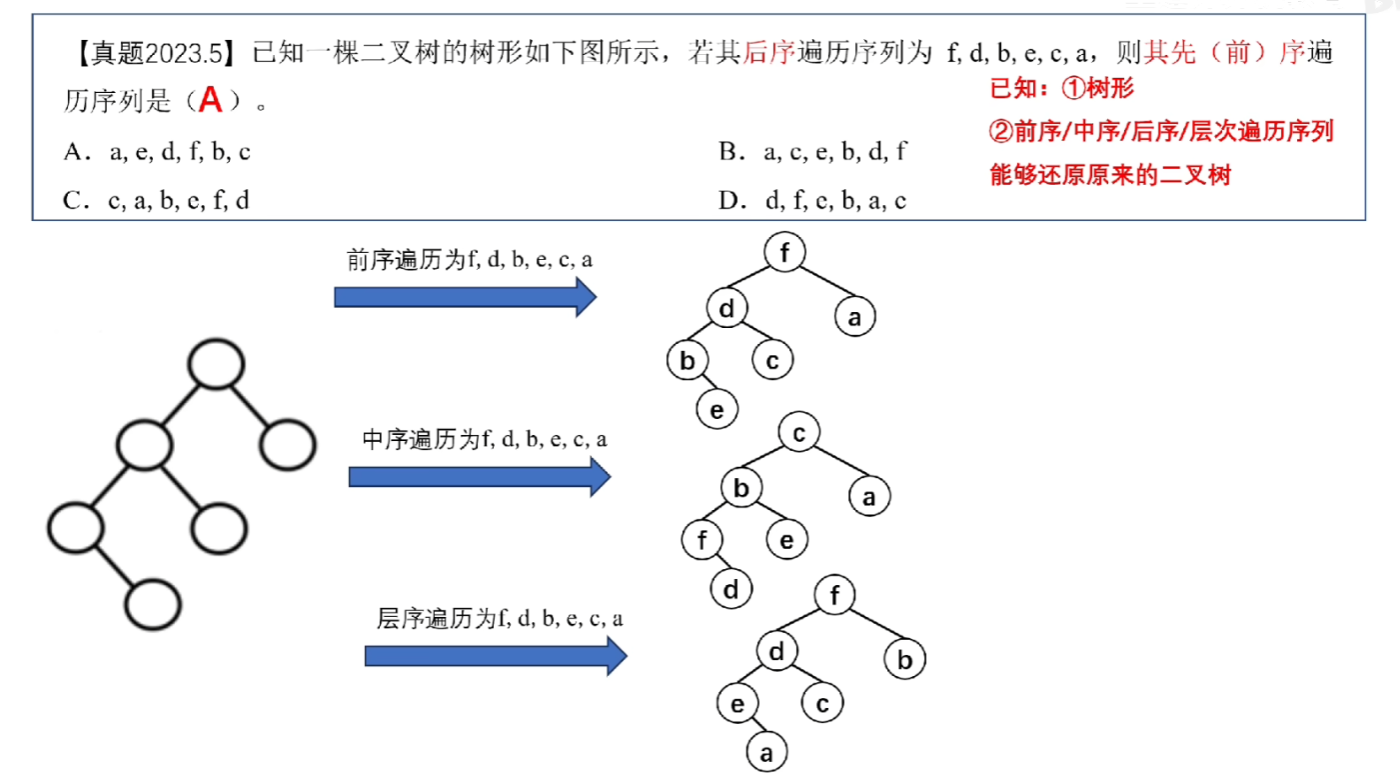
【层序+中序】
;
;
【一些技巧知识点】
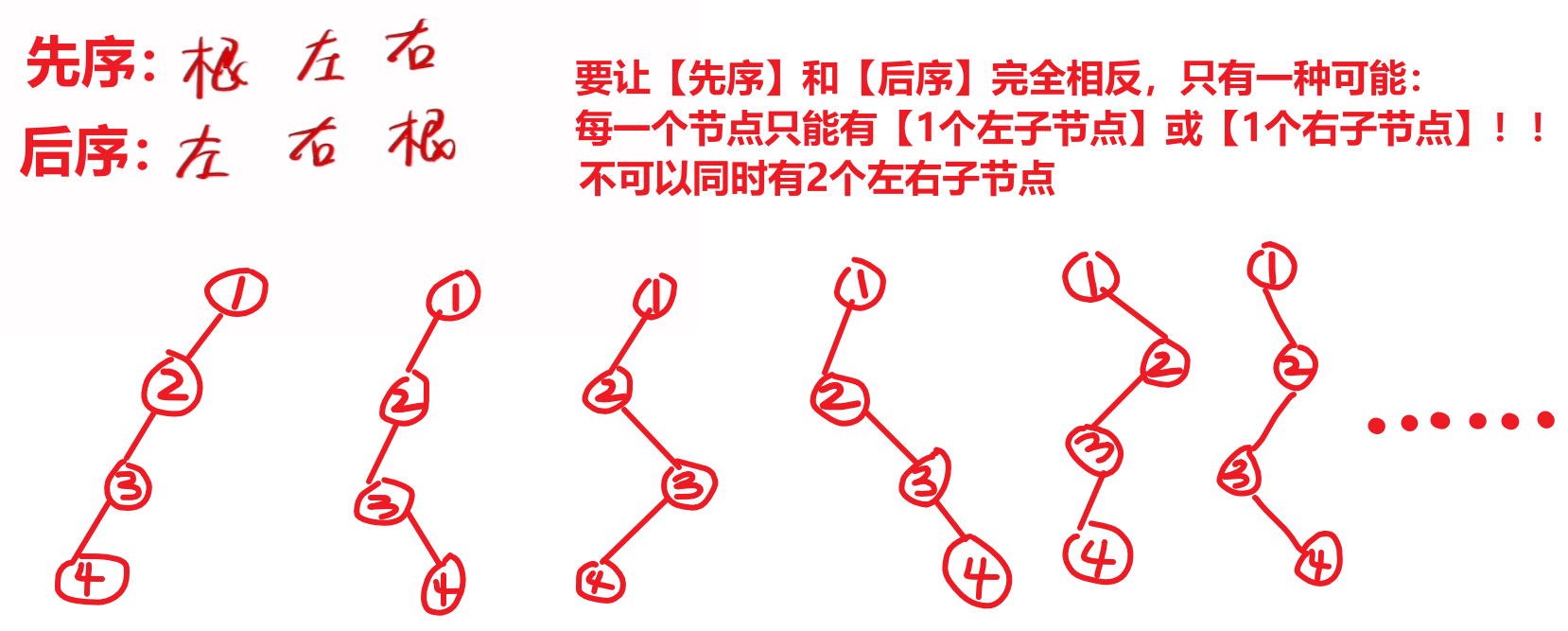
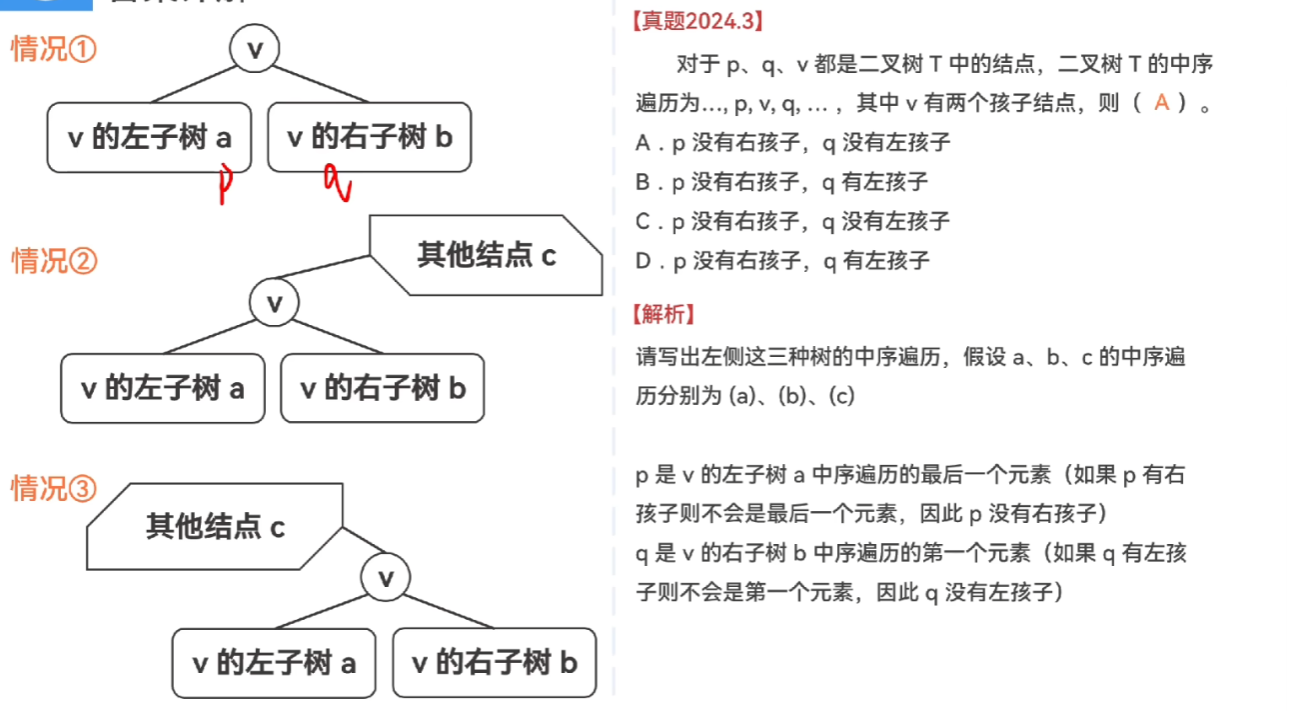
- 【先序遍历】和【后序遍历】完全不一样:该树的节点只有1左孩子、或只有1右孩子
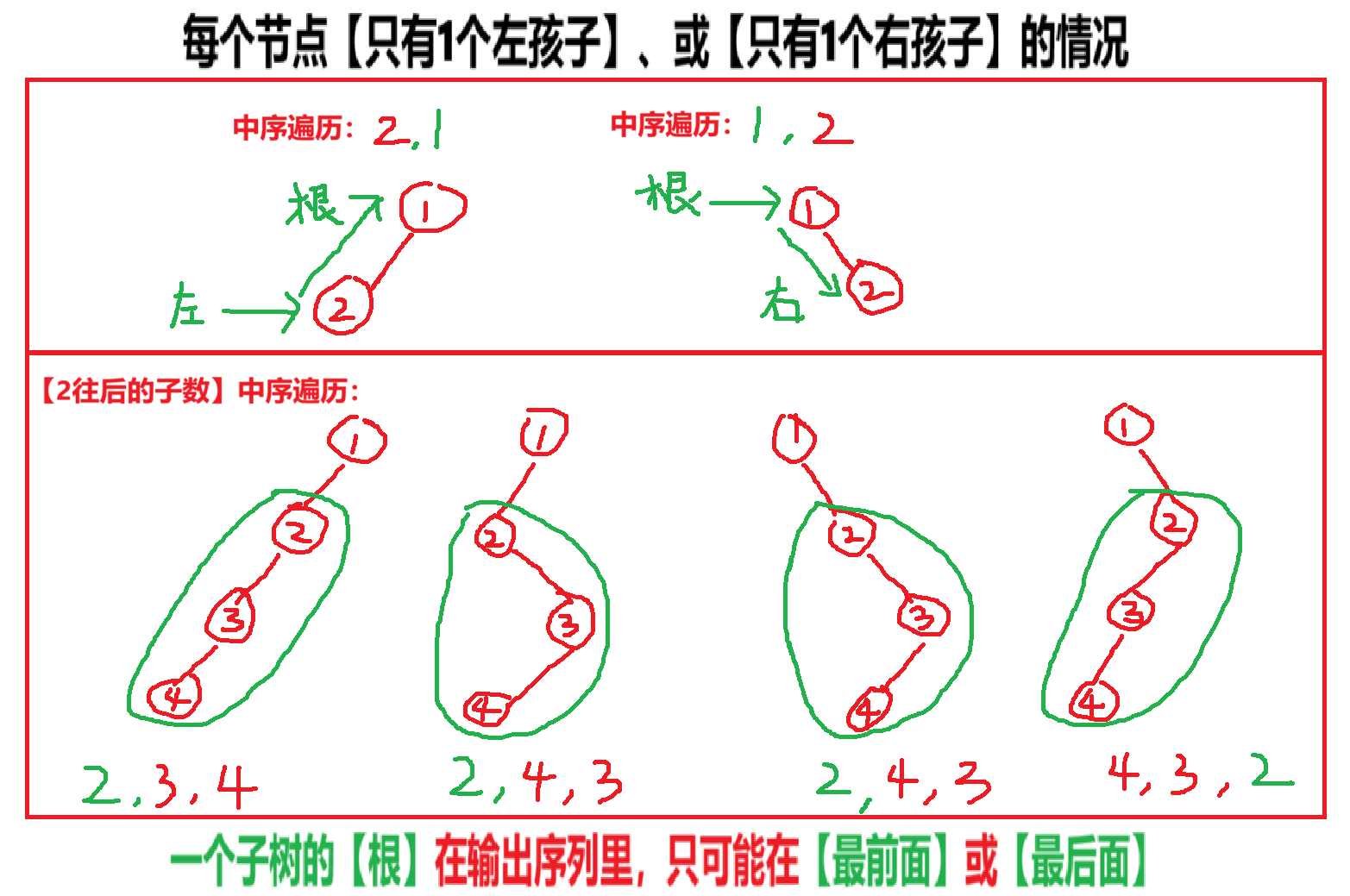
- 【中序遍历】对于“节点只有1左孩子、或只有1右孩子”的树,【子树根】只会在序列最前、或最后
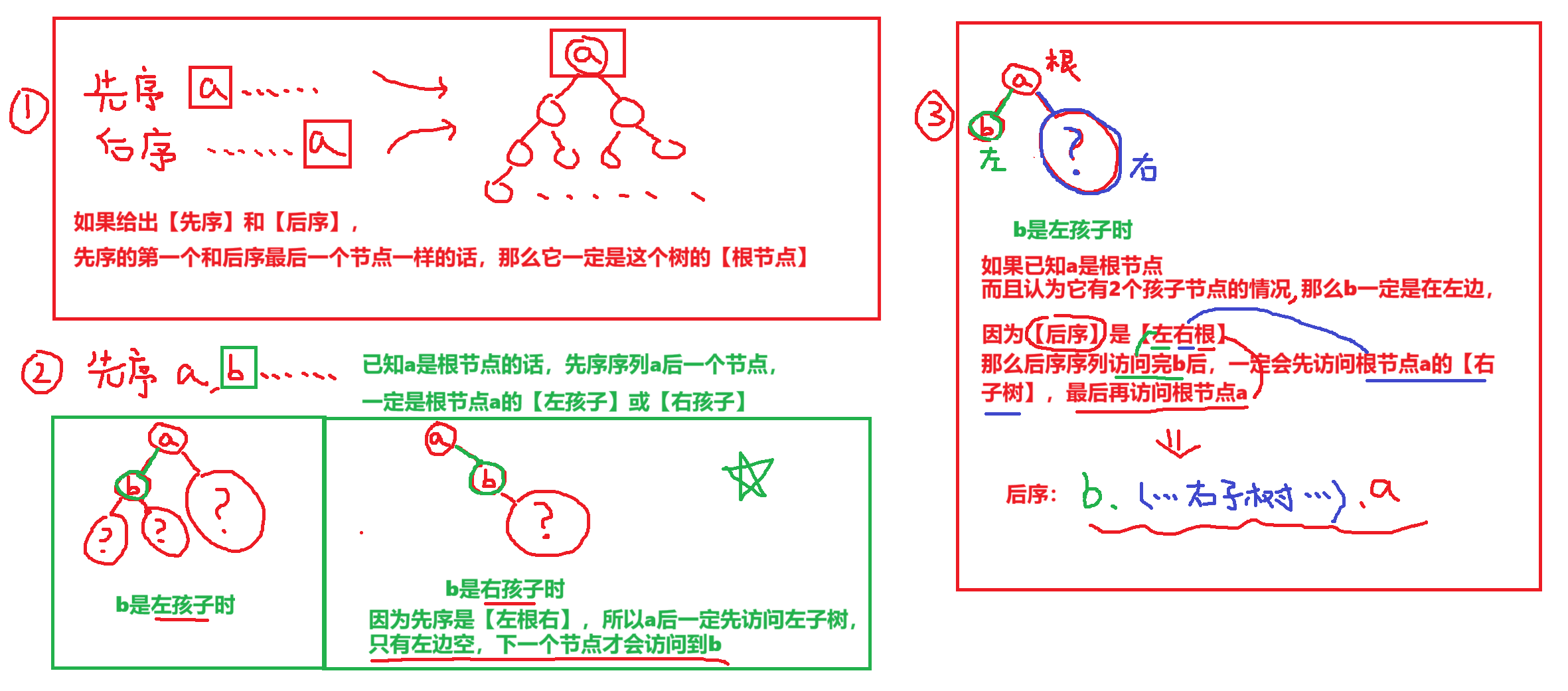
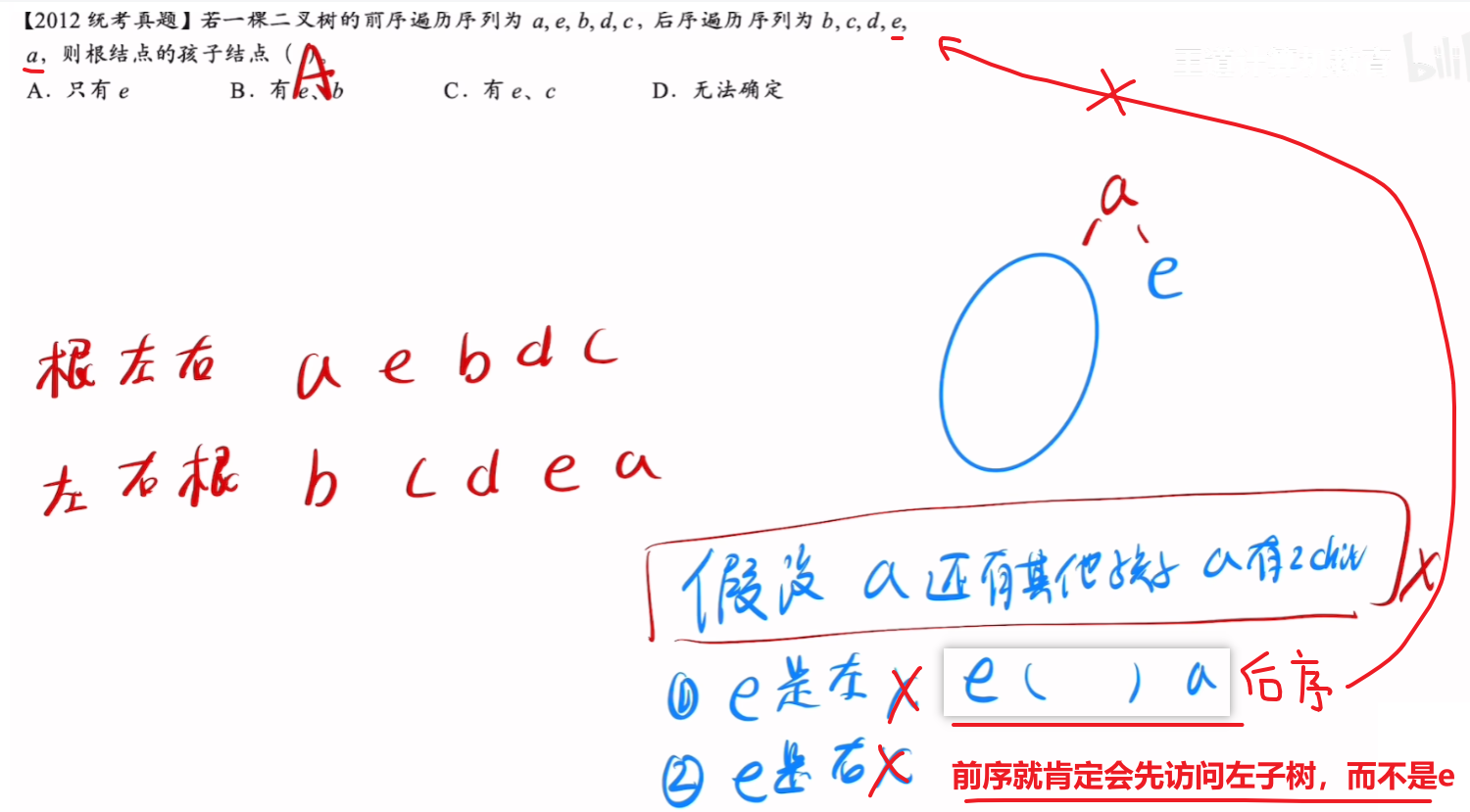
- 【只有前序、后序】时,并非什么也推不出
- 可以推出【根节点】、以及【紧挨根节点的左、右孩子】
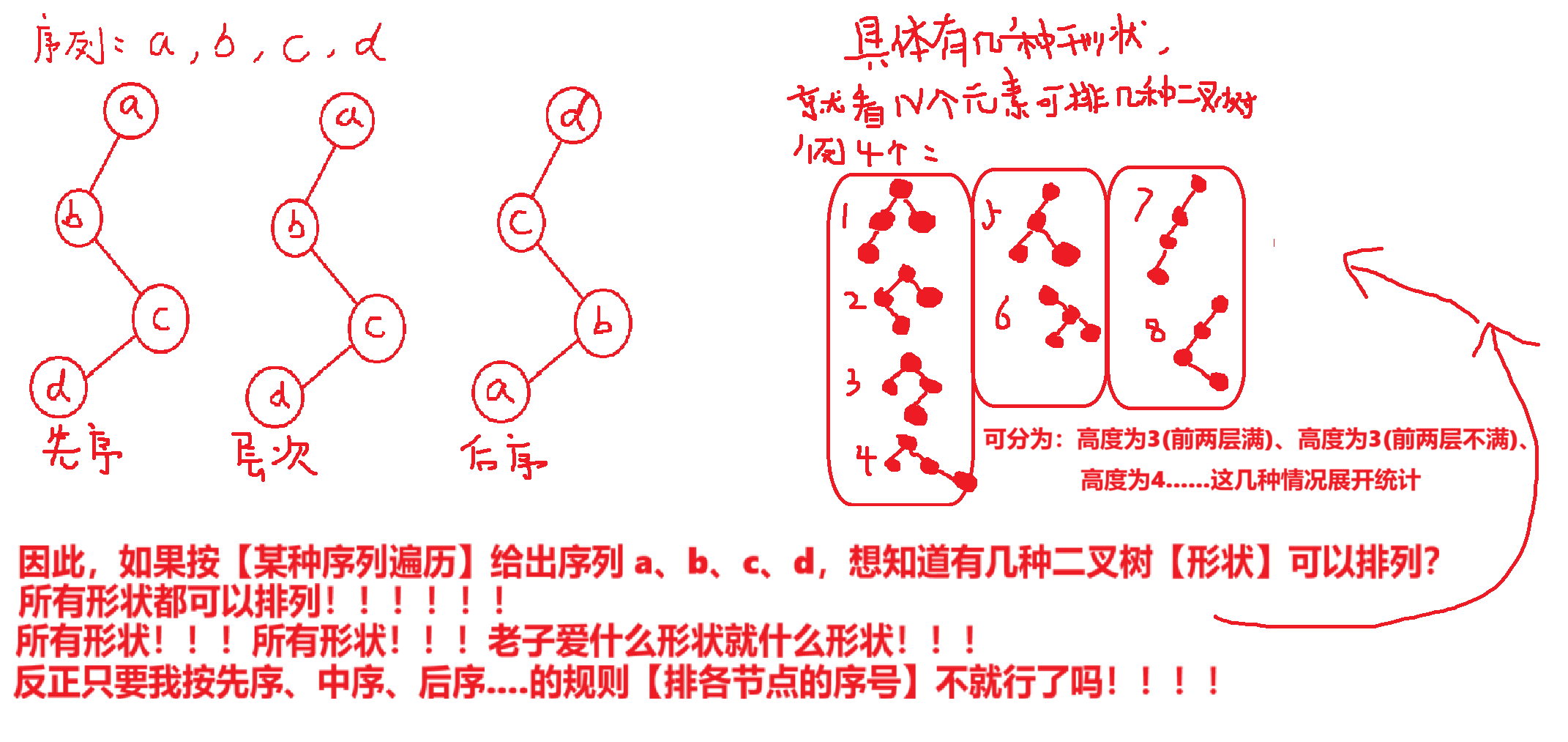
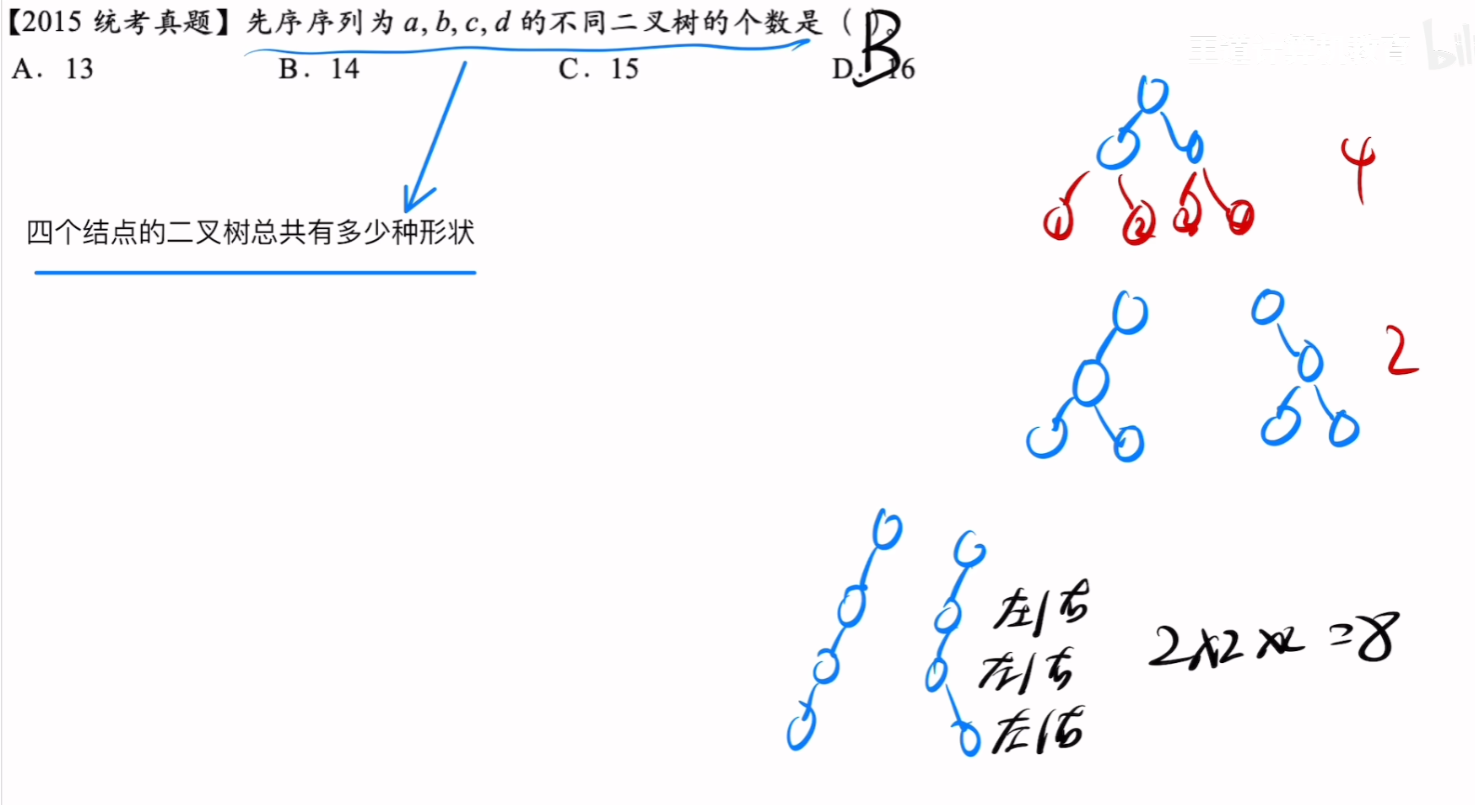
- 【任何遍历方式】输出了【N个元素的序列】,都对应有【
】种二叉树形状
- 也可以用【卡特兰数】来计算【n个节点的二叉树形状】
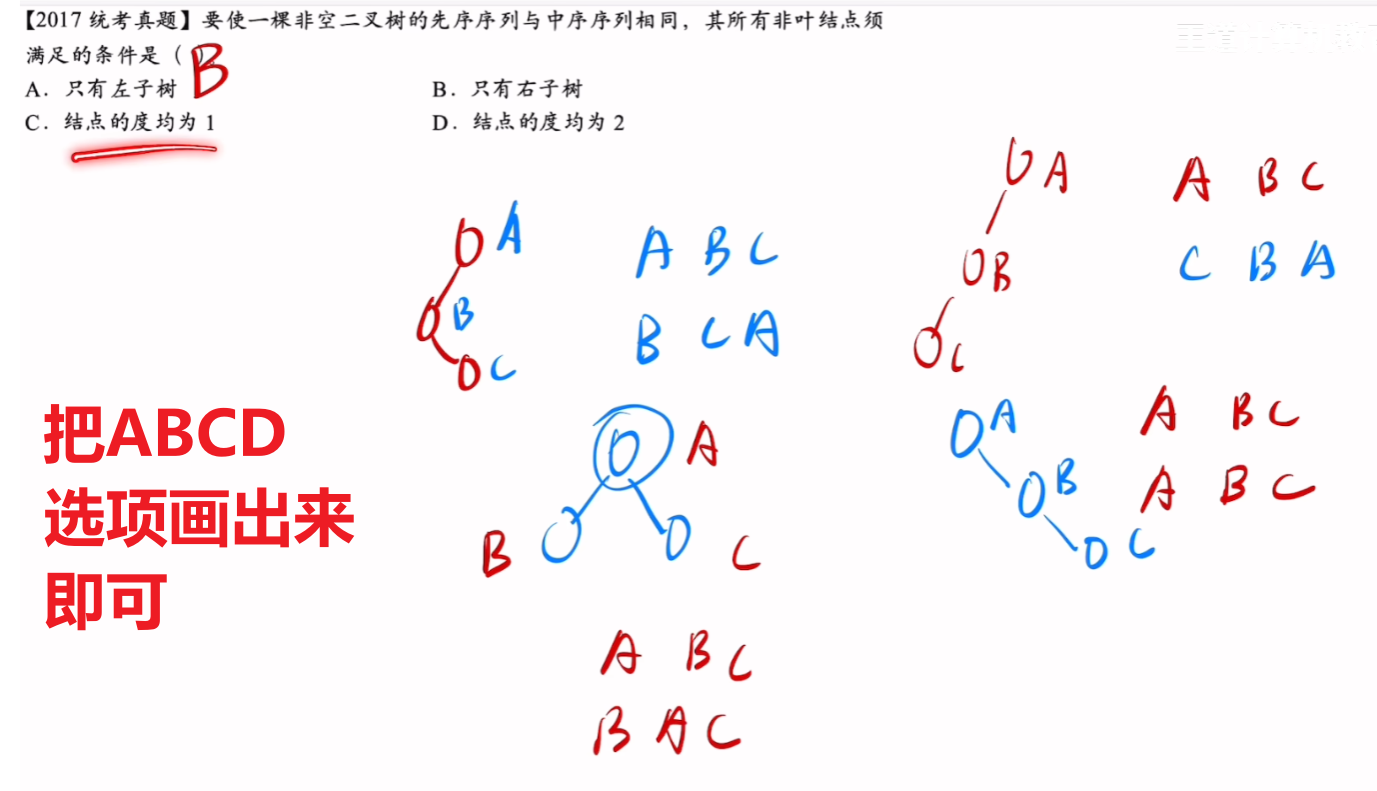
- 什么情况【先序=中序】、【后序=中序】
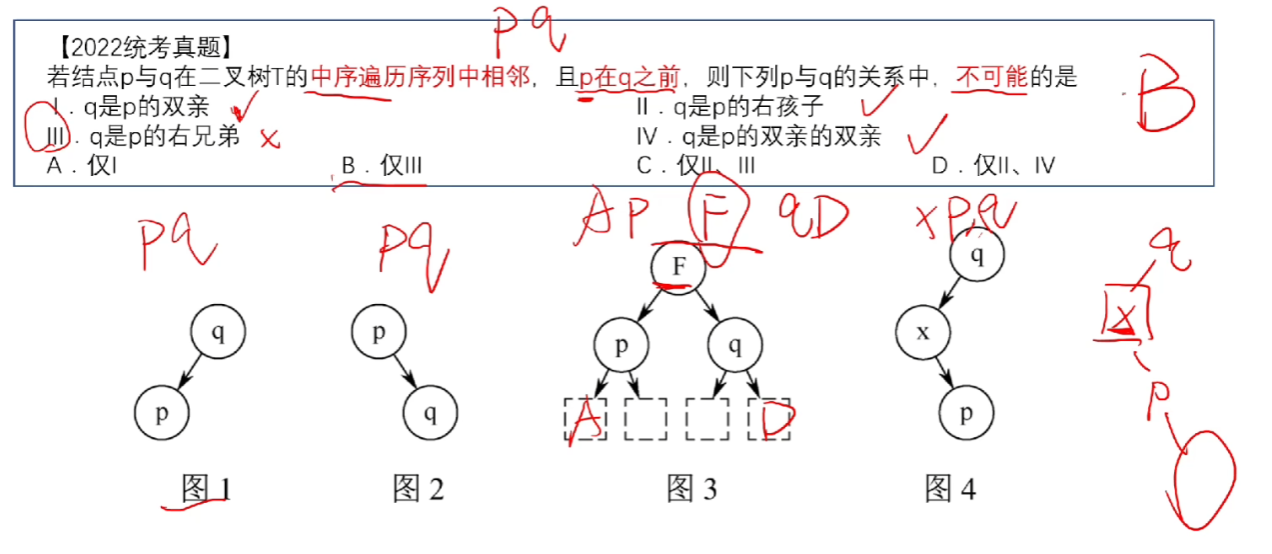
【例题】
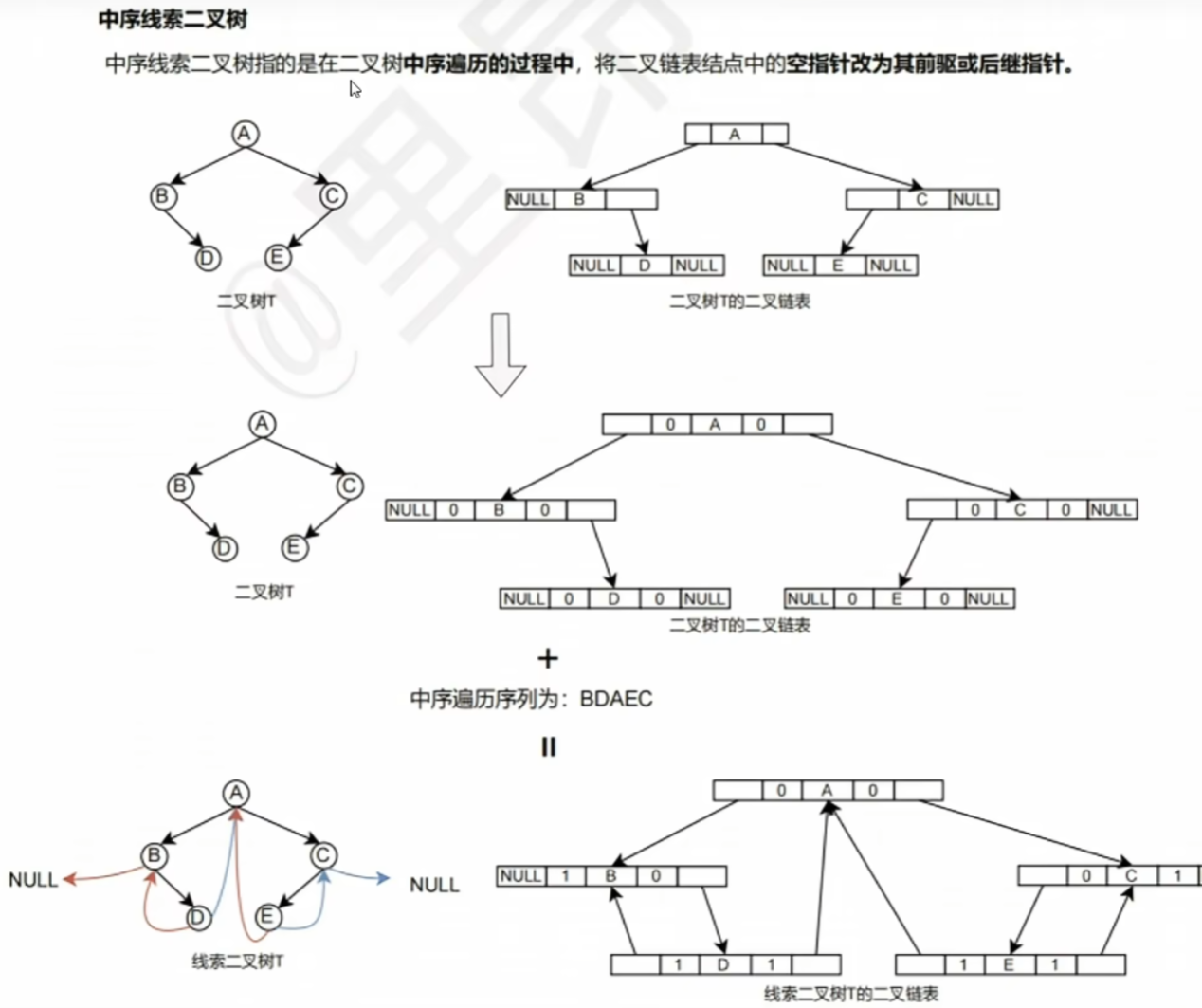
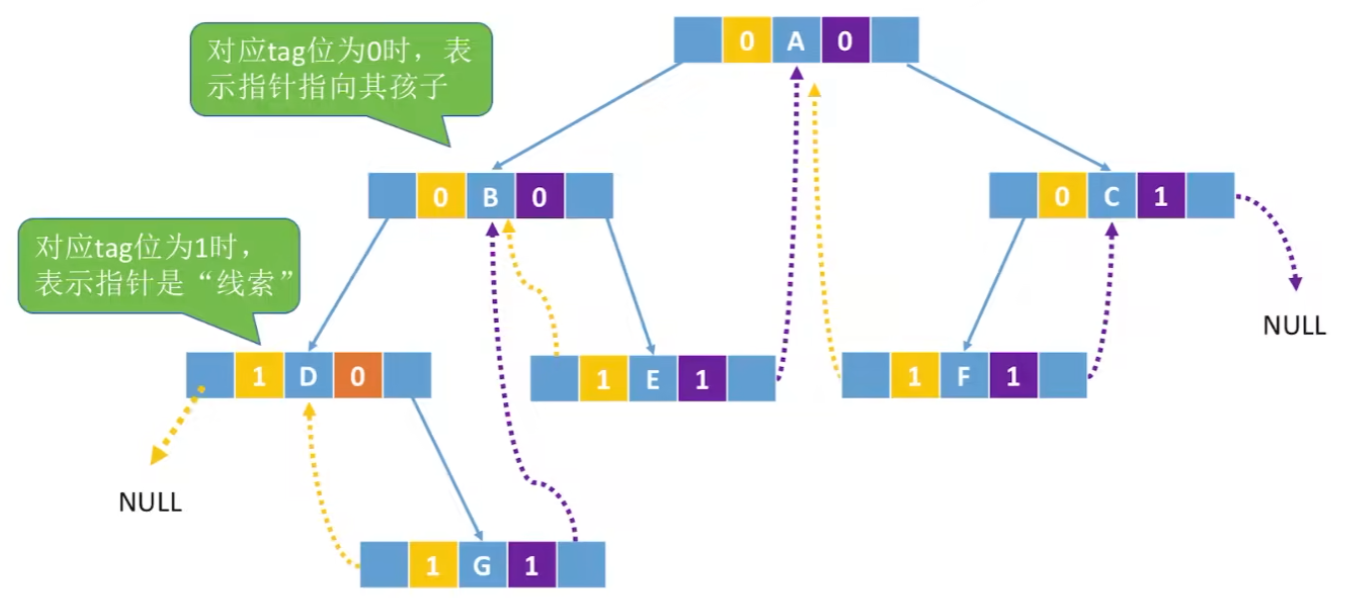
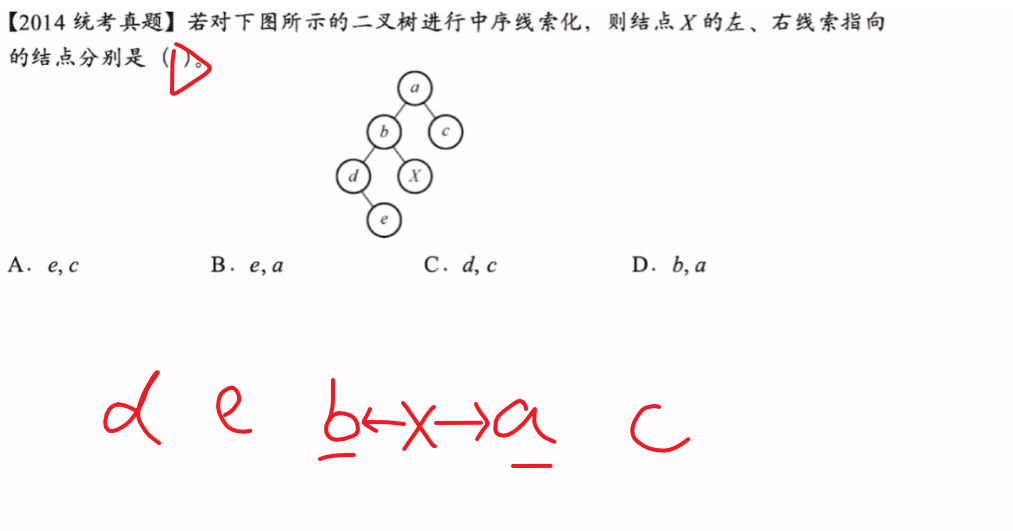
三、线索二叉树
【总结思维导图】
【具体解释】
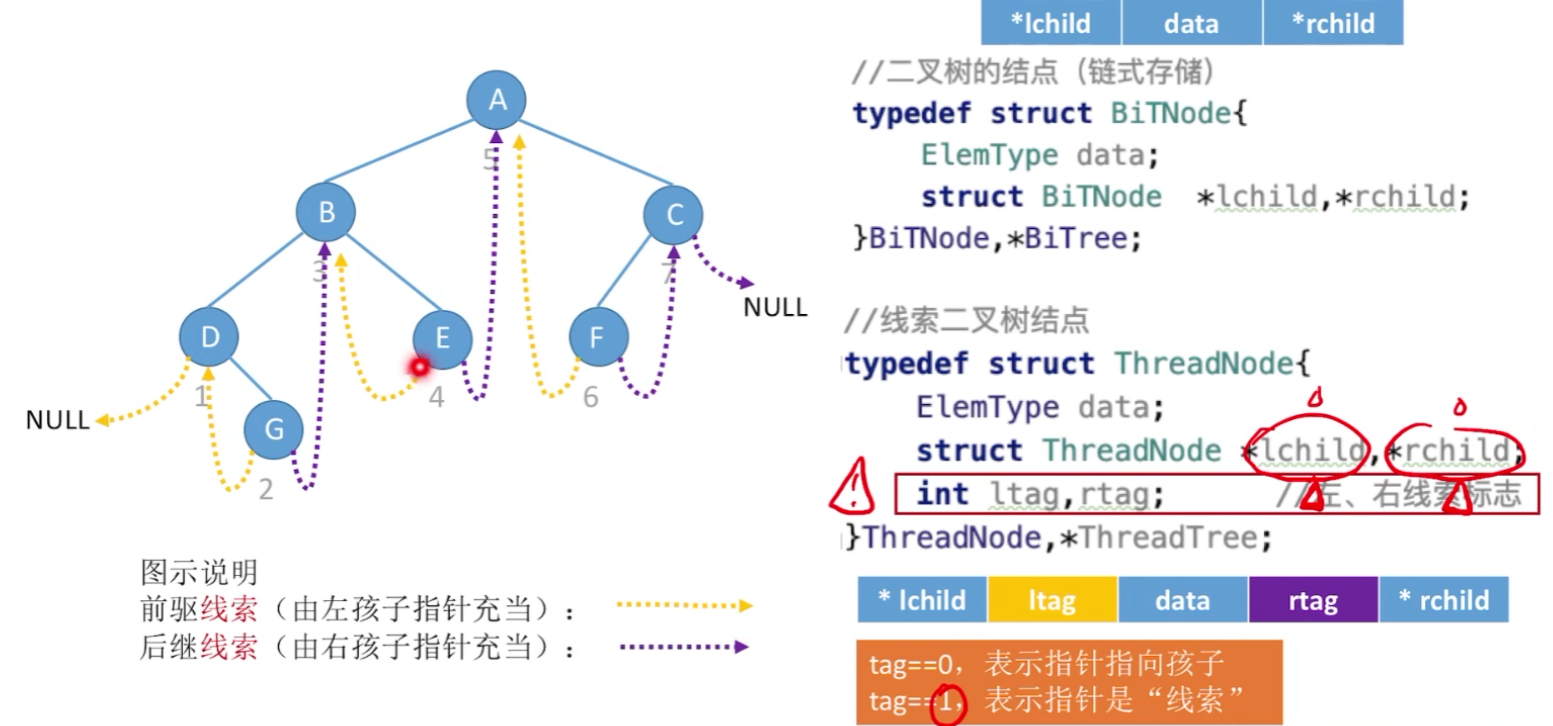
1)中序线索二叉树
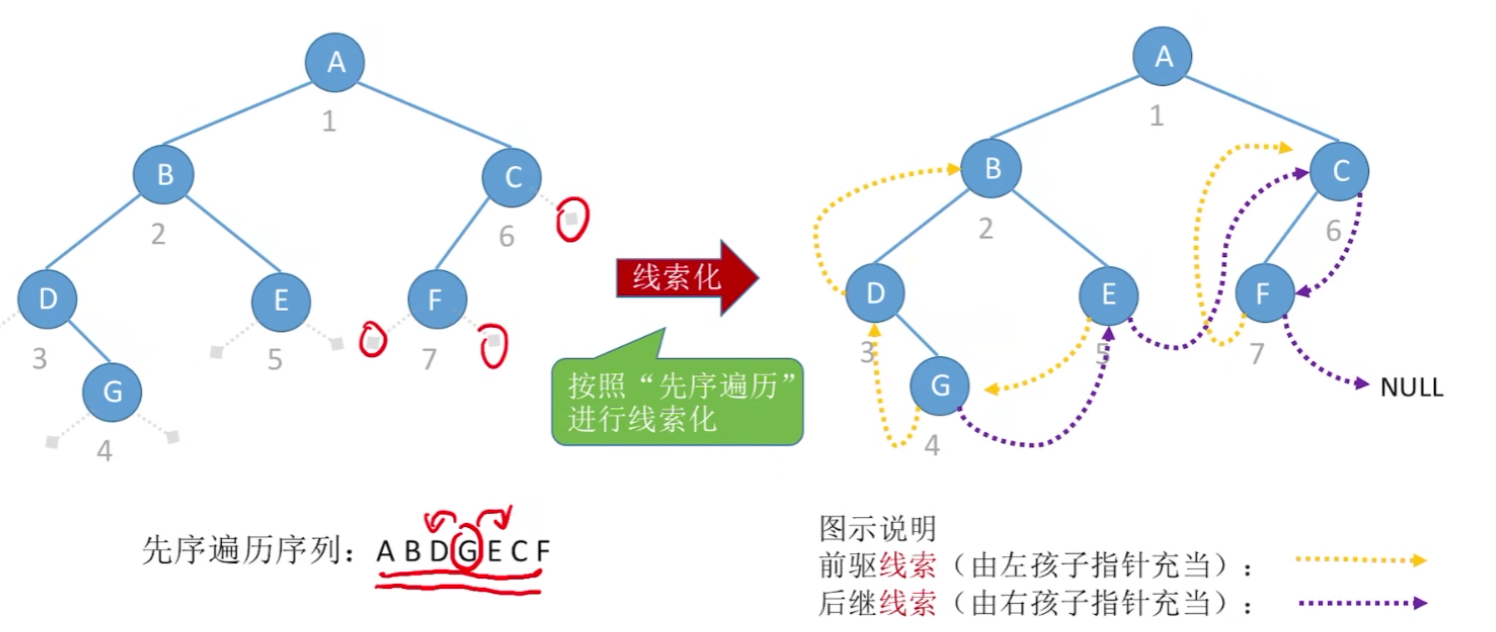
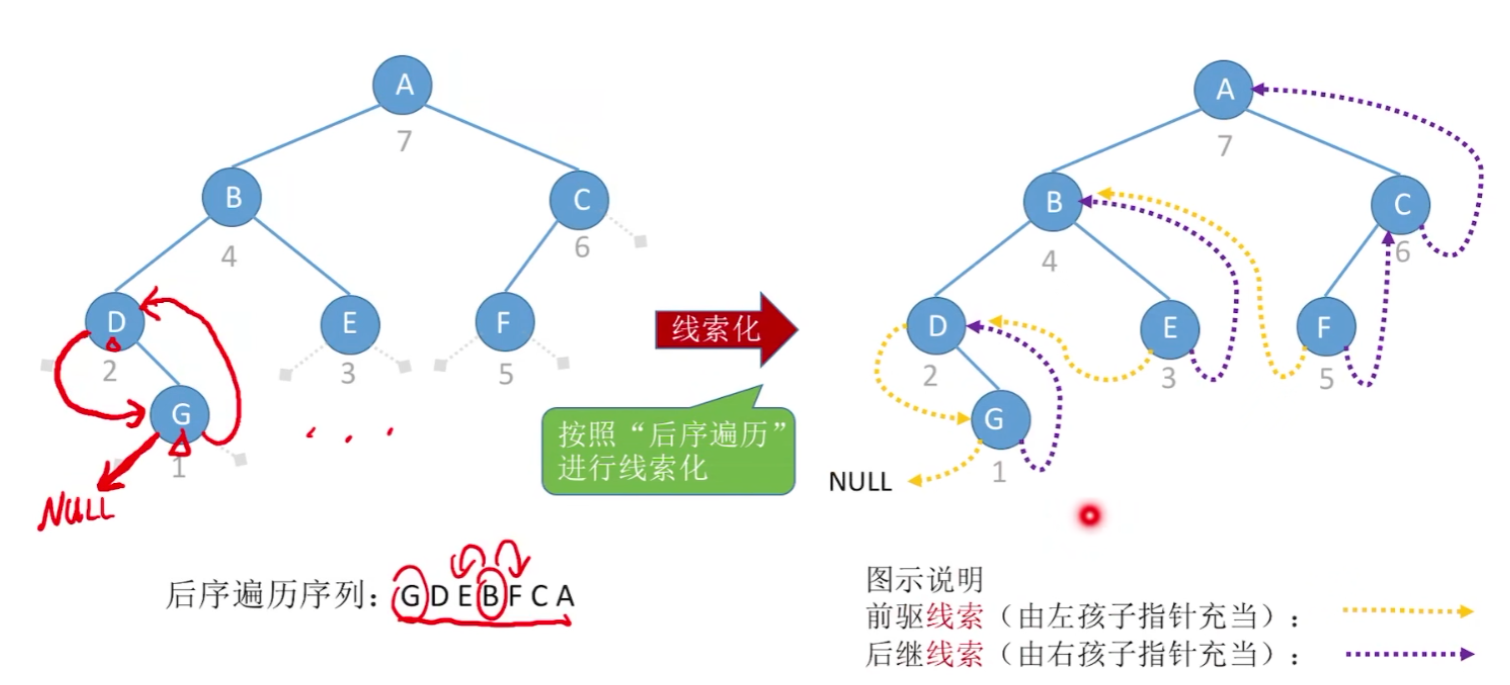
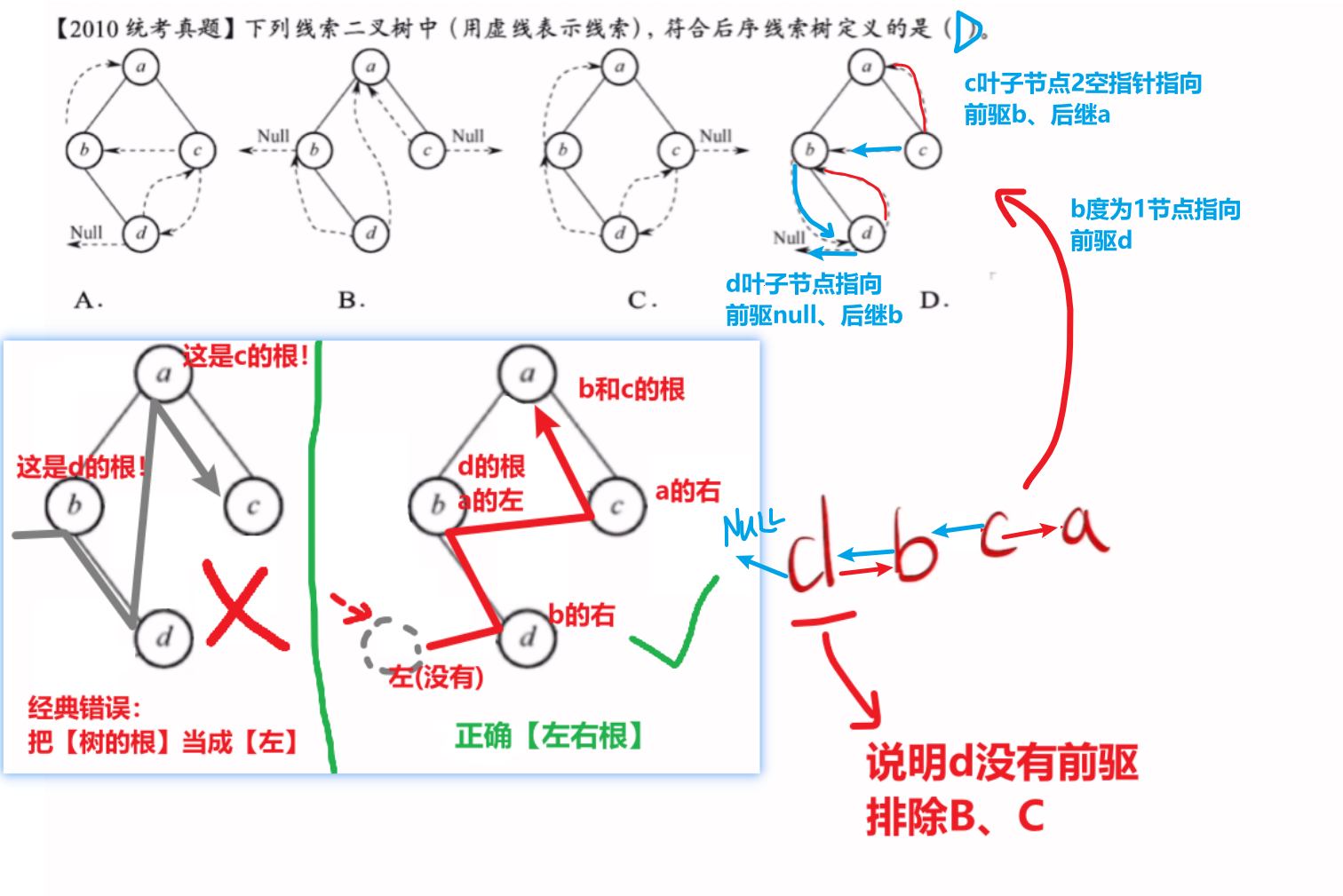
2)先序 和 后序线索二叉树
【先序遍历线索二叉树】
【后续遍历线索二叉树】