向量内积可看作 1 行 ×1 列的矩阵乘法，矩阵乘法则可拆成 多个向量内积的集合

向量内积可看作 1 行 ×1 列的矩阵乘法，矩阵乘法则可拆成 多个向量内积的集合

flyfish

两个列向量
$\vec{a}$ 是列向量，形式为 $\left[\begin{array}{c}{A}_1\\ A_2\\ A_3\end{array}\right]$（维度 $3\times 1$）。

$\vec{b}$ 是列向量，形式为 $\left[\begin{array}{c}{B}_1\\ B_2\\ B_3\end{array}\right]$（维度 $3\times 1$）。

转换过程

1. 符号与向量表示

${\vec{a}}^{\top }$ 是向量 $\vec{a}$ 的转置(右上角多个T)，将原本的列向量转化为行向量，形式为 $[A_1{A}_2{A}_3]$（维度 $1\times 3$）。

$\vec{b}$ 是列向量，形式为 $\left[\begin{array}{c}{B}_1\\ B_2\\ B_3\end{array}\right]$（维度 $3\times 1$）。

2. 矩阵乘法的运算过程

当行向量 ${\vec{a}}^{\top }$ 与列向量 $\vec{b}$ 进行矩阵乘法时，运算规则是“对应元素相乘后求和”：
$$\underset{{\vec{a}}^{\top }}{\underbrace{\left[A_1{A}_2{A}_3\right]}}\underset{\vec{b}}{\underbrace{\left[\begin{array}{c}{B}_1\\ B_2\\ B_3\end{array}\right]}}=A_1{B}_1+A_2{B}_2+A_3{B}_3$$

矩阵

设矩阵 $\mathbf{A}=\left[\begin{array}{ccc}{A}_{11}& A_{12}& A_{13}\\ A_{21}& A_{22}& A_{23}\\ A_{31}& A_{32}& A_{33}\end{array}\right]$（3×3矩阵），
矩阵 $\mathbf{B}=\left[\begin{array}{ccc}{B}_{11}& B_{12}& B_{13}\\ B_{21}& B_{22}& B_{23}\\ B_{31}& B_{32}& B_{33}\end{array}\right]$（3×3矩阵），
它们的乘积为矩阵 $\mathbf{C}=\mathbf{A}\times \mathbf{B}$，其中 $\mathbf{C}=\left[\begin{array}{ccc}{C}_{11}& C_{12}& C_{13}\\ C_{21}& C_{22}& C_{23}\\ C_{31}& C_{32}& C_{33}\end{array}\right]$（3×3矩阵

具体计算示例

以 $C_{11}$（第1行第1列）为例：
$$C_{11}=A_{11}{B}_{11}+A_{12}{B}_{21}+A_{13}{B}_{31}$$

以 $C_{12}$（第1行第2列）为例：
$$C_{12}=A_{11}{B}_{12}+A_{12}{B}_{22}+A_{13}{B}_{32}$$

3. 与向量内积的等价性

这个结果恰好就是向量内积的定义，即：
$$A_1{B}_1+A_2{B}_2+A_3{B}_3=\vec{a}\cdot \vec{b}$$

向量内积（点积）的几何表示为：
$$\vec{a}\cdot \vec{b}=|\vec{a}|\cdot |\vec{b}|\cos \theta$$

其几何意义是：$\vec{a}$ 在 $\vec{b}$ 上的投影长度（$|\vec{a}|\cos \theta$）与 $\vec{b}$ 的模长（$|\vec{b}|$）的乘积（也可理解为 $\vec{b}$ 在 $\vec{a}$ 上的投影与 $|\vec{a}|$ 的乘积，结果等价）。

怎么变的看这里
向量内积的 基于长度和夹角 与 基于坐标乘积求和是等价的,即几何定义是如何推导为代数形式的

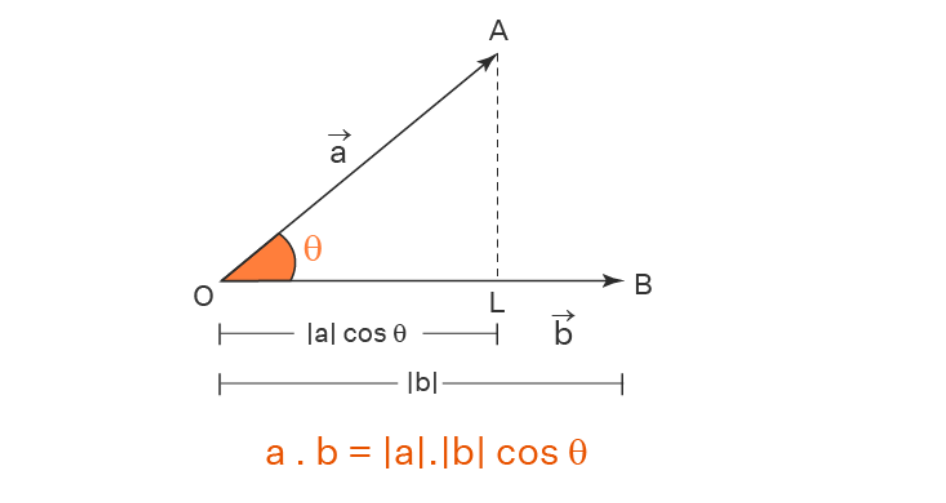
意思是
向量 $\vec{a}$：从点 $O$ 指向点 $A$ 的有向线段，模长为 $|\vec{a}|$；
向量 $\vec{b}$：从点 $O$ 指向点 $B$ 的有向线段，模长为 $|\vec{b}|$；
夹角 $\theta$：$\vec{a}$ 与 $\vec{b}$ 之间的夹角；
投影线段 $OL$：从 $A$ 向 $\vec{b}$ 所在直线作垂线，垂足为 $L$，则 $OL$ 的长度为 $|\vec{a}|\cos \theta$（即 $\vec{a}$ 在 $\vec{b}$ 方向上的投影长度）。