随笔——记一次常见的浮点数精度问题到Grisu3初识
背景介绍
某天下午在工位被逆天AI编辑器干晕后,和朋友互相吐槽。朋友说到了他正好在查一个浮点数问题。问我要不要换换脑子一起来看。

发来了一个断点截图,乍一看相当的诡异。又问了下每个变量的数据类型。这个orgin[i][1]是一个int,而percent是一个float,是通过策划配置的万分比整形6000转换出来的。不少人这里应该已经猜到了。这是个经典的浮点数精度问题。换成double以后就好了。不过本着换脑子的目的,发现了两个让人感兴趣的点。具体可看这段简单的示意代码(把数字做了点简化,效果是一样的)
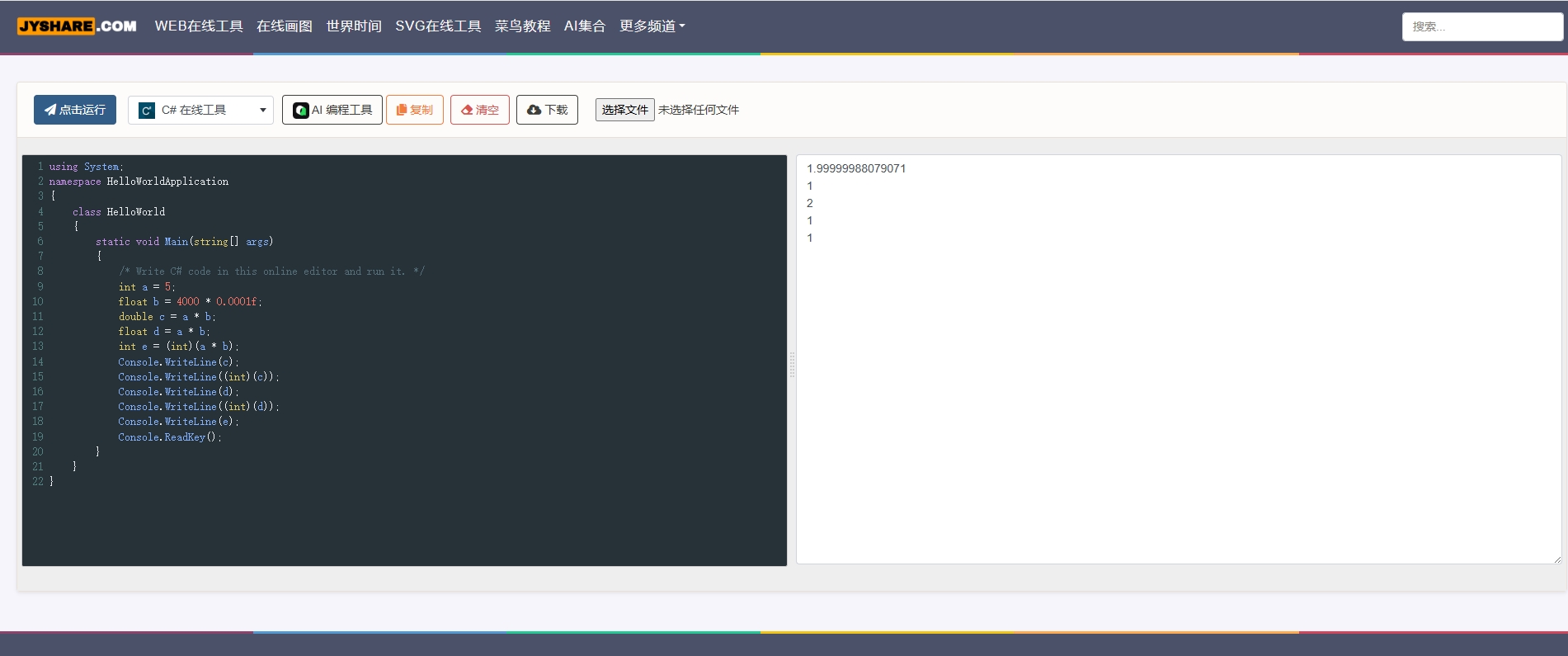
- 小数点后四位的精度 float就撑不住了吗
- debug断点面板和Console是如何打印浮点数的,和(int)的区别是什么
四位精度就干住了吗?
首先,我们需要回忆下我们的计算机组成原理基础知识。需要用到下面三个基础。这里默认大家有基本的了解基本是一笔带过。
- 十进制小数的二进制存储和表示
- 浮点数标准
- 二进制乘法计算方法
我们知道数字在计算机里是用二进制存储表示的,0.5,0.25这种是二进制下的有限小数。而0.4,0.6之类的则是无限小数。根据存储的位数不同,最后一定会丢失部分的精度。
Float是一个四字节32位的浮点数数据结构。根据IEEE 754 标准,它由1位符号位,8位指数位
,和23位精度位组成。
我们利用接口 把他们的bytes转换出来 ,再按大端序小端序整理并按照标准拆分精度为位符号位和指数位。并且加上精度位隐藏的先导1。
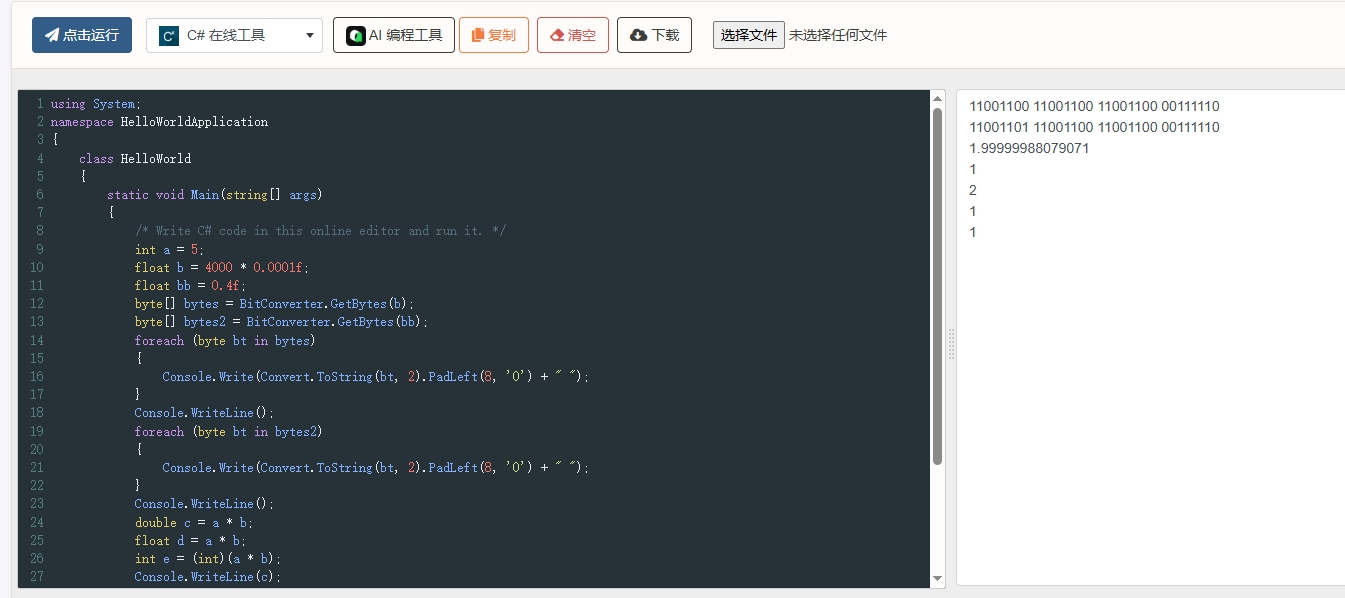
得到了0.4的精度位是1.10011001100110011001100
而4000 * 0.0001的精度位则是1.10011001100110011001101
区别是最后一位是1
而我们乘5 等于左移两位后相加,前者正好全是1,后者因为最后多的1发生了进位
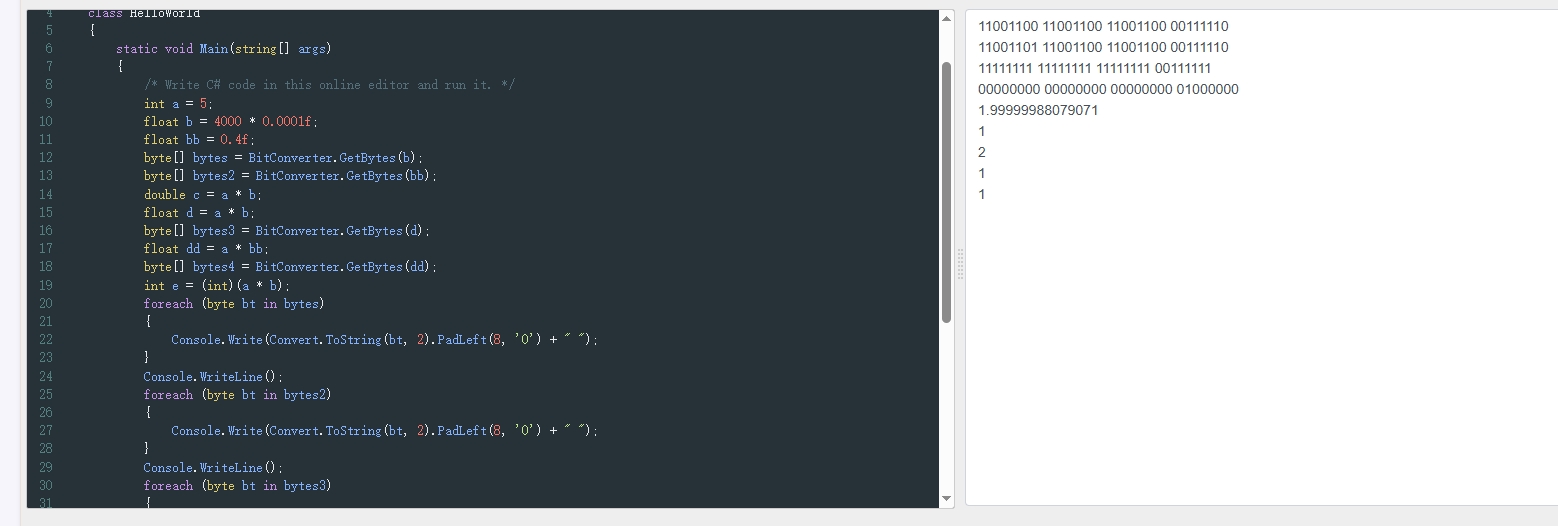
浮点数到底是怎么显示和转换的
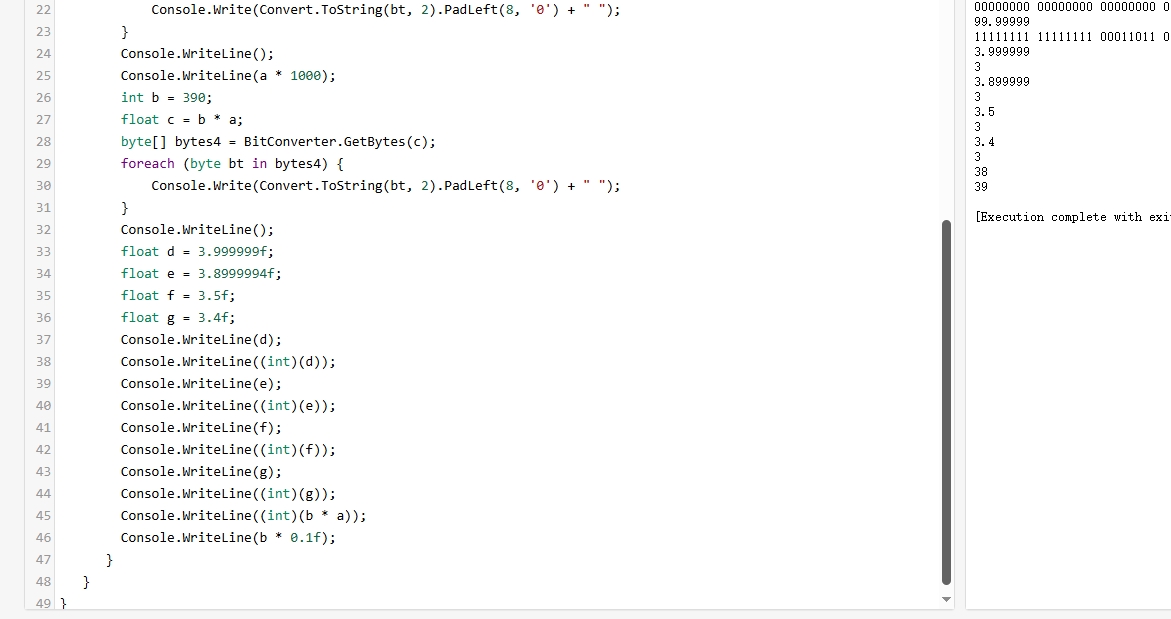
问题到这里本来告一段落了,但是紧接着我们可以注意到一个奇怪的现象,那就是直接输出float的时候的值和(int)转换后不一致。(int)是去尾法的转换,那直接输出float的时候呢?这里是怎么把一个float类型输出成一个整数或者一个多位小数的呢?看起来是带上一些精度的四舍五入。我又试了几次,如下图。遂打开源码一探究竟。
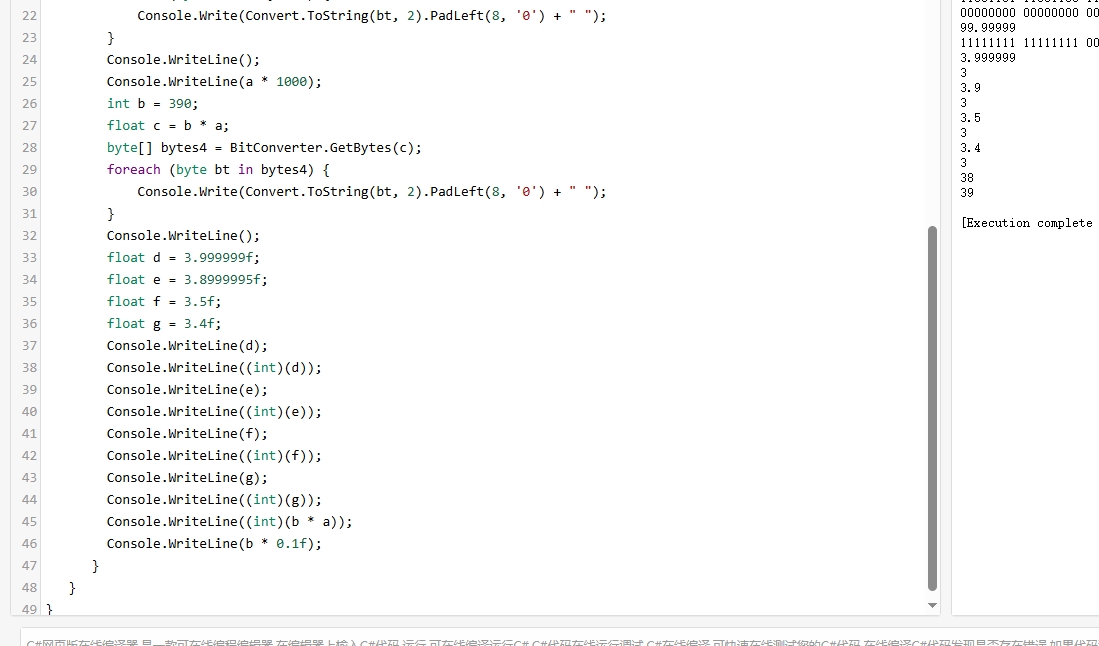
Grisu3
简单的查阅了一下源码后,找到了答案。其实是有专门的算法去做这个事情的,去找到最短的可还原的浮点数的表示。简单来说就是本来有一个比较慢的算法去做这个事情,可以做到百分百正确。后来提出了一个优化算法Grisu,有小概率情况不正确,但是快很多。后来结合了一下推出了Grisu3,正确的情况用快的,判断会不正确的话就用慢的。
具体可以参考这个论文:Grisu3
另外推荐一下这篇知乎文章,目前笔者还是很难做到边写边读,边想到指令集级别的处理。只有在做个别优化的时候会想到这些。希望日后也能达到这个境界吧
---->知乎文章
