圈地游戏（分数规划、网格图对偶建模）

原题链接：圈地游戏

题目大意

叮咚鸡家里有一块地，由 $n$ 列 $m$ 行的方格组成，各自内种的菜有一定的价值，并且每一条单位长度的格线有一定的费用。叮咚鸡喜欢在地里散步，它可以从任意一个格点出发，沿着格线行走直到回到出发点，且在行走途中不允许与已走过的路线有任何相交或接触（出发点除外）。记这条封闭路线内部的格子总价值为 $V$，路线上的费用总和为 $C$，叮咚鸡想知道 $\frac{V}{C}$ 的最大值是多少。
样例输入：
第一行为两个正整数 $n,m$。
接下来 $n$ 行，每行 $m$ 个非负整数，表示对应格子的价值。
接下来 $n+1$ 行，每行 $m$ 个正整数，表示所有横向的格线上的费用。
接下来 $n$ 行，每行 $m+1$ 个正整数，表示所有纵向的格线上的费用。

3 4
1 3 3 3
1 3 1 1
3 3 1 0
100 1 1 1
97 96 1 1
1 93 92 92
1 1 90 90
98 1 99 99 1
95 1 1 1 94
1 91 1 1 89

样例输出：

1.286

题目分析

• 这是典型的分数规划结合网络流的题目，对于最终收益的最大值 $\frac{V}{C}$，假设当前二分的值为 $\lambda$，那么有 $\frac{V}{C}>\lambda$，也就是说当 $V-\lambda \times C>0$ 时当前 $\lambda$ 未达到最大值，需要调整下界 $l$ 为 $\lambda$；反之则需要调整上界 $r$ 为 $\lambda$。
• 考虑如何计算 $V-\lambda \times C$ 的最大值，对于网格图，很自然想到用网格图的对偶图建模，由于网格中无自然流的流向确定，因此将每一个网格视为选或者不选的问题,，而选或不选的问题又常常可以被转化为最小割问题。
• 采取最大权闭合图思想寻找最大化 $V-\lambda \times C$ 的选择方案：$$\max (P_{sel}-Cost)=\sum P_{all}-\min \text{Cut}$$取源点 $S$，汇点 $T$，从每个 $S$ 向每个格点连边，容量为该格点权值；从每个格点向四周连边，容量为对应接触的边的权值，如果为外部面，则向 $T$ 连边，即 $T$ 视作外部面标号。考虑下简化图结构：
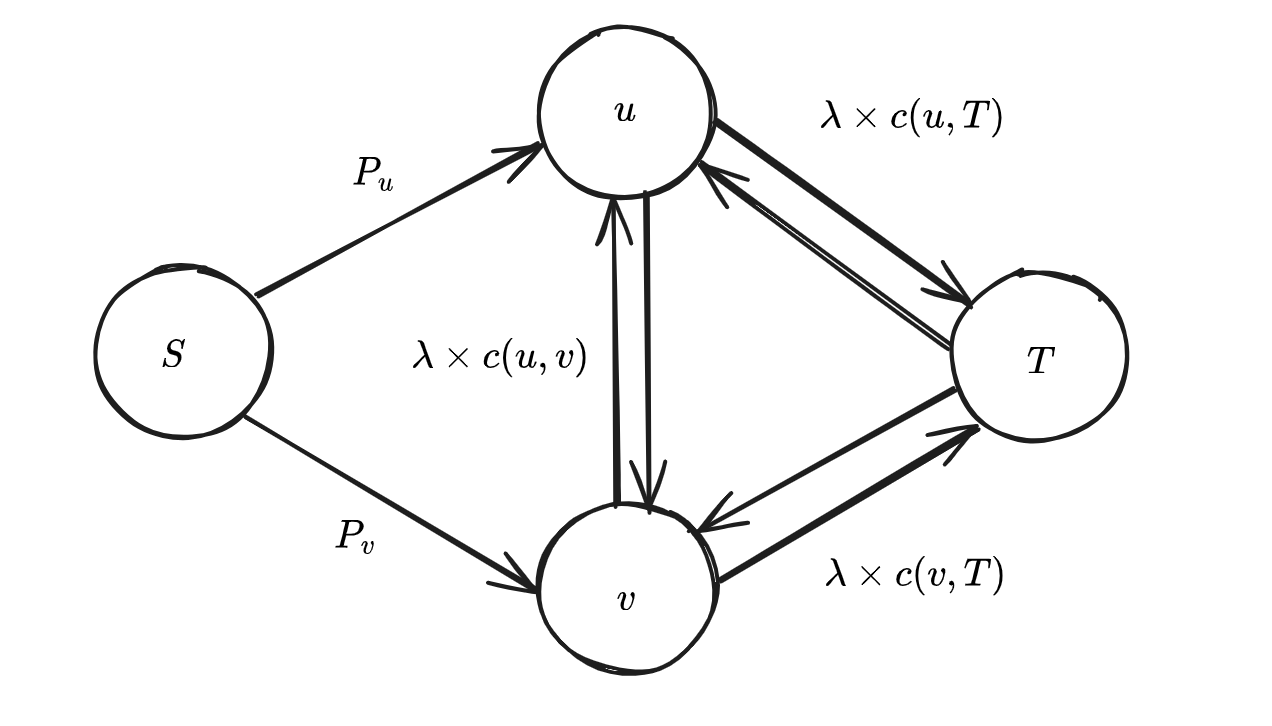
  对于价值边，如果不选择 $u$，那么最小割需要加入 $P_u$；对于代价边，其发生在相邻两节点一个被选一个不被选的情况，如若此时不选择 $u$ 但选择了 $v$，为了彻底割去 $u$，最小割在加入 $P_u$ 的基础上还要加上 $\lambda \times (c(u,v)+c(v,T)$。
• 在建图时可用如下形式对索引为 $idx$ 的横边或者竖边映射到对偶图中的对应两个节点。用 $up$ 和 $down$ 表示标号为 $idx$ 的横边上下的节点标号；用 $left$ 和 $right$ 表示标号为 $idx$ 的竖边左右的节点标号。

int up(int idx) {return (idx <= m ? T : idx - m);}
int down(int idx) {return (idx > n * m ? T : idx);}
int left(int idx) {return ((idx % (m + 1)) == 1 ? T : idx - (idx - 1) / (m + 1) - 1);}
int right(int idx) {return ((idx % (m + 1)) == 0 ? T : idx - idx / (m + 1));}

代码答案

#include<bits/stdc++.h>
#define endl '\n'
#define ll long longusing namespace std;const int N = 3e3 + 10, M = 5e5 + 10;
const double DINF = 1e18;
int n, m, tot = 1, rd[M], cd[M], bx[N][N], S, T;
int d[N], cur[N], head[N];int sgn(double x) {if(fabs(x) < 1e-6) return 0;return x > 0 ? 1 : -1;
}struct edge {int v, nxt; double c;
} edges[M];int up(int idx) {return (idx <= m ? T : idx - m);}
int down(int idx) {return (idx > n * m ? T : idx);}
int left(int idx) {return ((idx % (m + 1)) == 1 ? T : idx - (idx - 1) / (m + 1) - 1);}
int right(int idx) {return ((idx % (m + 1)) == 0 ? T : idx - idx / (m + 1));}void add(int u, int v, double c, int k = 1) {edges[++tot] = {v, head[u], c};head[u] = tot;edges[++tot] = {u, head[v], k * c};head[v] = tot;
}bool bfs() {fill(d, d + N, 0);queue<int> q;d[S] = 1; q.push(S);while(q.size()) {int u = q.front(); q.pop();for(int i = head[u]; i; i = edges[i].nxt) {int v = edges[i].v;if(!d[v] && sgn(edges[i].c) > 0) {d[v] = d[u] + 1;q.push(v);if(v == T) return true;}}}return false;
}double dfs(int u, double mf) {if(u == T) return mf;double s = 0;for(int i = cur[u]; i; i = edges[i].nxt) {cur[u] = i;int v = edges[i].v;if(d[v] == d[u] + 1 && sgn(edges[i].c) > 0) {double res = dfs(v, min(mf - s, edges[i].c));edges[i].c -= res;edges[i ^ 1].c += res;s += res;if(sgn(s - mf) == 0) break;}}if(sgn(s) == 0) d[u] = 0;return s;
}double dinic() {double flow = 0;while(bfs()) {memcpy(cur, head, sizeof head);flow += dfs(S, DINF);}return flow;
}int main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);cin >> n >> m;S = 0, T = n * m + 1;for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++)	cin >> bx[i][j];}for(int i = 1; i <= n + 1; i++) {for(int j = 1; j <= m; j++) cin >> rd[(i - 1) * m + j];}for(int i = 1; i <= n; i++) {for(int j = 1; j <= m + 1; j++) cin >> cd[(i - 1) * (m + 1) + j];}auto check = [&](double lam) -> bool {tot = 1;fill(head, head + N, 0);double s = 0;for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {add(S, (i - 1) * m + j, bx[i][j], 0);s += bx[i][j];}}for(int i = 1; i <= n + 1; i++) {for(int j = 1; j <= m; j++) {int idx = (i - 1) * m + j;add(up(idx), down(idx), lam * rd[idx]);}}for(int i = 1; i <= n; i++) {for(int j = 1; j <= m + 1; j++) {int idx = (i - 1) * (m + 1) + j;add(left(idx), right(idx), lam * cd[idx]);}}return sgn(s - dinic()) > 0;};double l = 0, r = DINF;while(sgn(r - l) > 0) {double mid = (r + l) / 2;(check(mid) ? l : r) = mid;}cout << fixed << setprecision(3) << l << endl;return 0;
}