202.快乐数

一、读题

题目来源：https://leetcode.cn/problems/happy-number/description/

    题目很简单，把题目给的一个数拆出来，每一位都计算自己的平方，然后相加，一直循环直到平方和为1，当平方和为1的时候循环结束，也有可能不会遇到1一直循环。如果遇到了1就返回true，如果一直遇不到1陷入循环就返回false；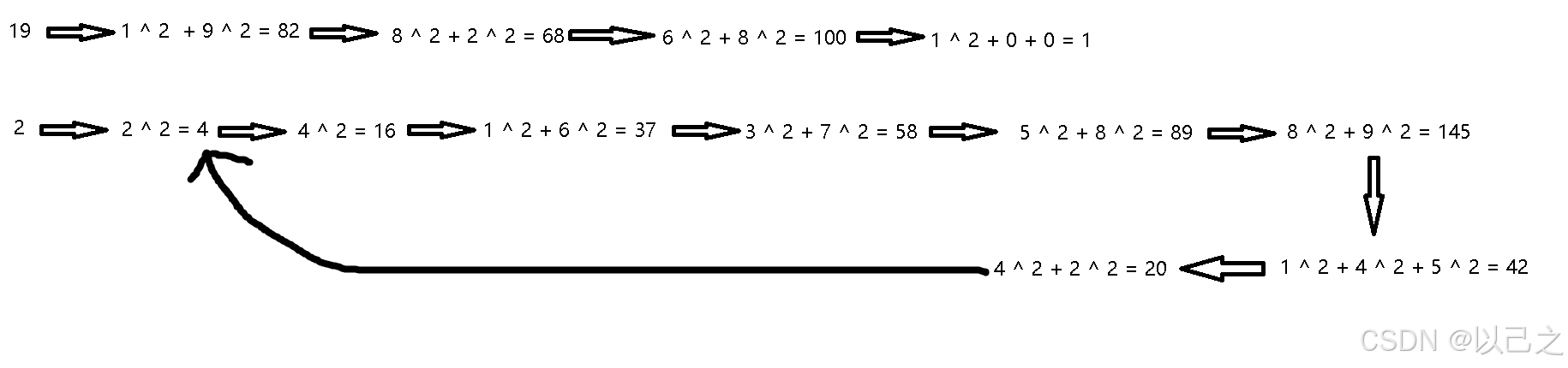

二、算法思路

     我们查看题目，结果只会有两种情况，一种是遇到1不进入循环，一种是进入循环出不来了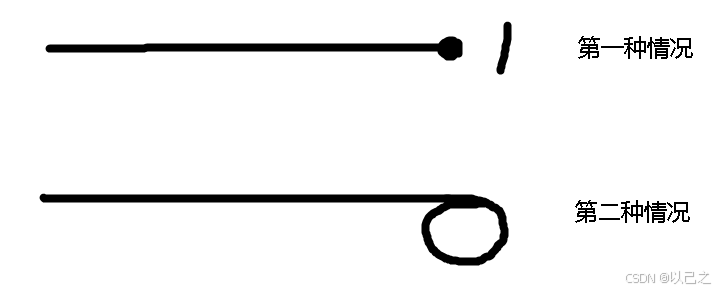
     但是我们仔细想，第一种情况真的不进入循环吗？不不不实际上两个情况都是循环，1的平方和是1，因此看起来像是没有进入循环，但是实际上是和第二种情况一样的，进入循环内出不来了。那么就很简单了，我们只需要判断环内的元素是否为1 即可。

     那既然理解了这种情况，那么解题思路就很简单了，不知道大家有没有做过一道题，就是学习集合的时候的一道算法题，判断链表是否有环，和这道题非常相似，这一道题是已知有环，判断环内的元素是否是1，我们只需要进入到环内了只会就判断环内元素是否是1即可。

     这一道题主包的思路是使用双指针。大家不要被这个名字局限了，一定要数组下标或者是某一个真正的指针才可以使用这个算法，双指针只是一个思想，那这一道题来说，如果是判断链表是否有环就可以将指针设置为链表的节点，那么这一道题就需要一个数据结构来配和使用指针来解题吗？不是的，我们前面说过不要被双指针这个名字局限到了，我们可以直接用这个平方和作为指针，而指针的下一个指针就是当前指针的各位平方和。

     那么我们只需要定义两个指针（快慢指针），一个指针走一步，另一个指针走两步，那么当进入环后，两个指针一定会遇见彼此，当遇到的时候（其实就是两者相同的时候）判断该指针数是否是1即可。

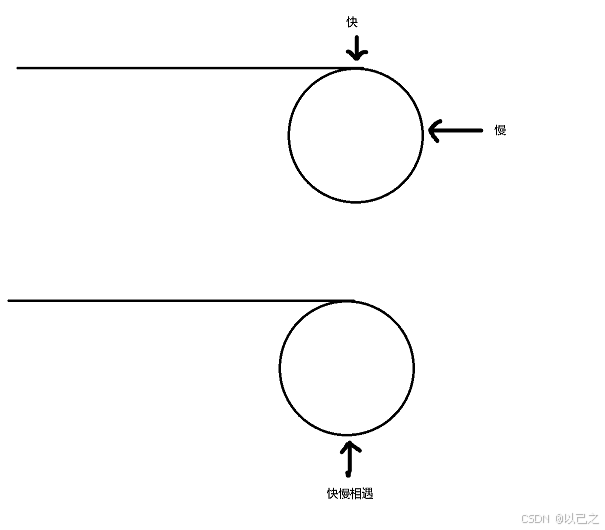
     （因为快慢指针一个速度快，一个速度慢，两倍速度的关系，当路程相同的情况下，一个指针到达终点那么另一个指针就一定是到达中点也就是一半的路程，当两个指针都进入环后，两个指针在相同的圆圈内往下走，慢指针永远比快指针少走一半的路程，那么就变成了高中物理的追及相遇问题，快指针走二分之一的路程，那么慢指针就走四分之一的路程，当快指针已经走完一圈的时候慢指针走一半，这个时候快指针再走二分之一，慢指针到四分之三，那么两者的距离越来越近，最终一定会相遇的）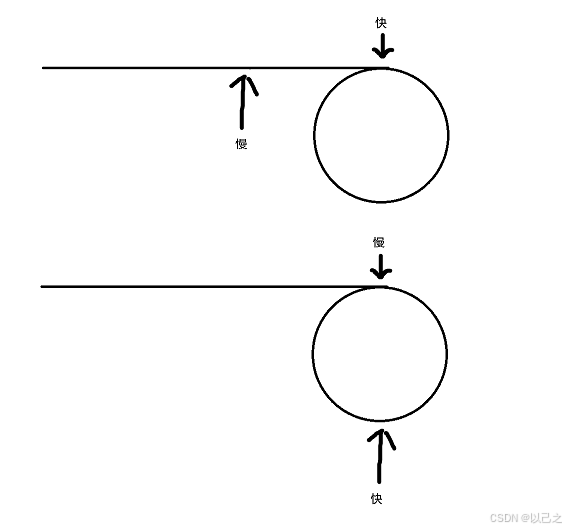

三、代码实现：

class Solution {public int function(int n) {int ans = 0;while(n != 0) {int ret = n % 10 ;ans += (ret * ret);n /= 10;}return ans;}public boolean isHappy(int n) {int i = n;int j = function(n);while(i != j) {i = function(i);j = function(function(j));if(i == j) break;}return i == 1;}
}

    各位佬，如果有什么更加高效的算法欢迎评论区讨论，指导一下主包进步，大家一起共勉