参考线模块(上)
决策规划总体概览

上述是最简单的静态障碍物情况,我们由简到难
参考线概述
参考线是为了解决如下问题:
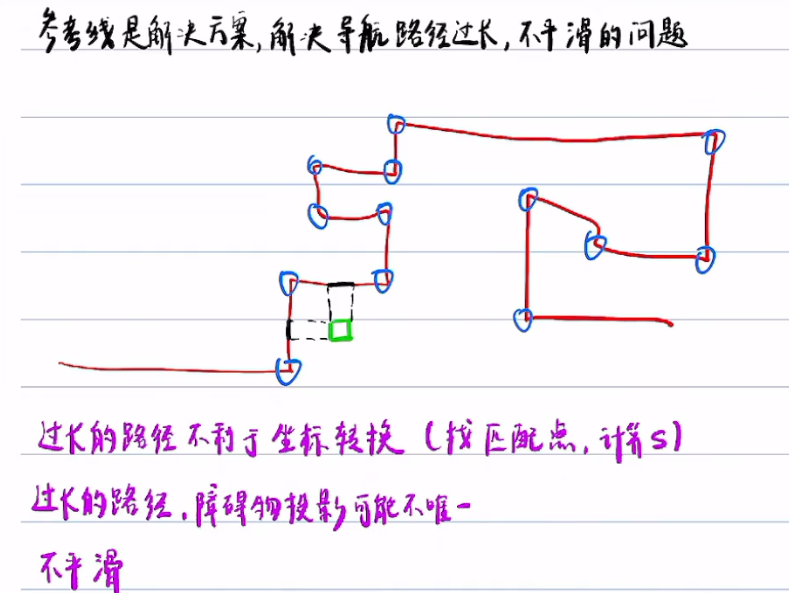
参考线:
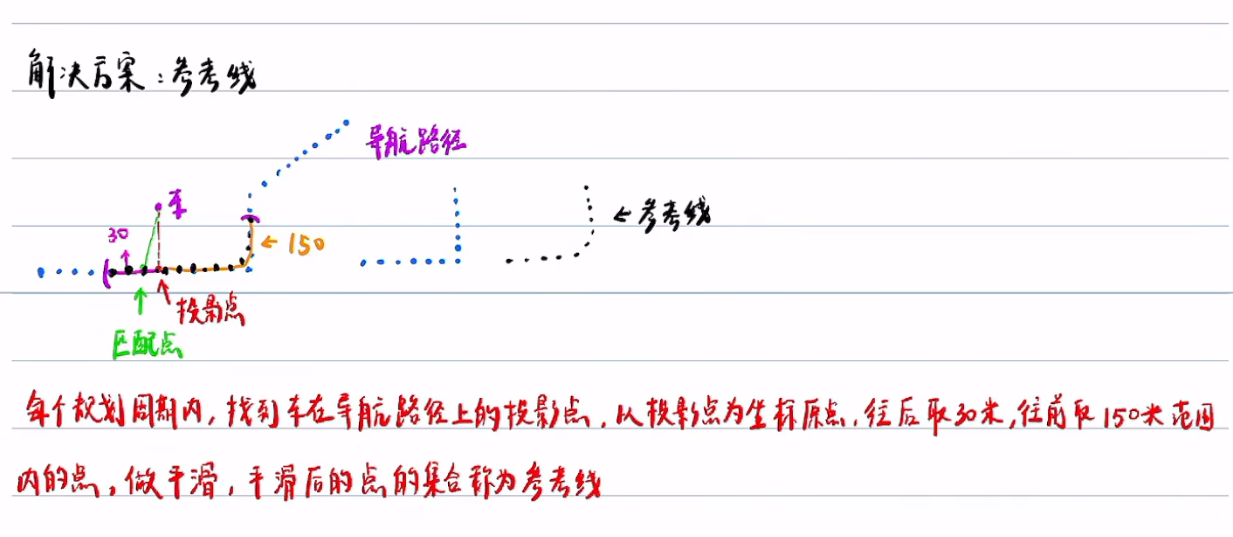
匹配点是距离最近的真实的路径散点,投影点是假想的点
参考线平滑算法
先来考虑最简单的(3个点)情况:
(1)衡量是否平滑,看||的大小
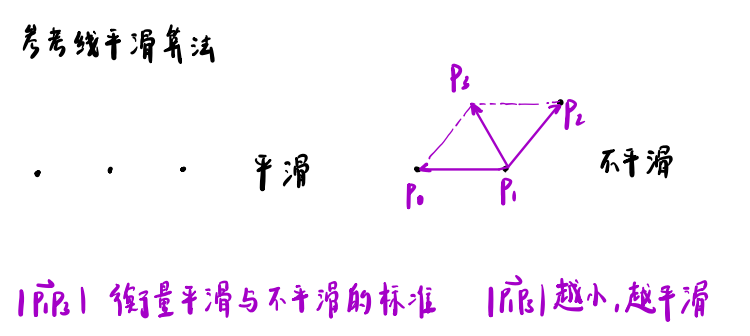
(2)有时平滑了,但几何上差距过大,我们要求的是与原路径点相似:

(3)几何形状的差距缩小后,长度尽量均匀紧凑:
图中绿线不好,我们希望的是紫线

综上,我们得到代价函数:

上图里的“s.t.”指 subject to,受限制于.../使得…满足…的意思(or “such that”),类似于约束条件
解释一下平滑代价:(紫色向量=两个黑色向量相加)

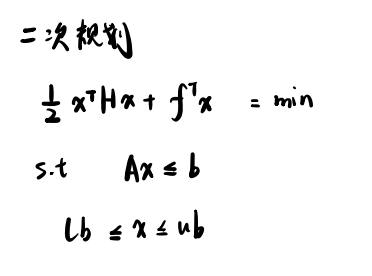
平方和 可以写成 向量*向量的转置
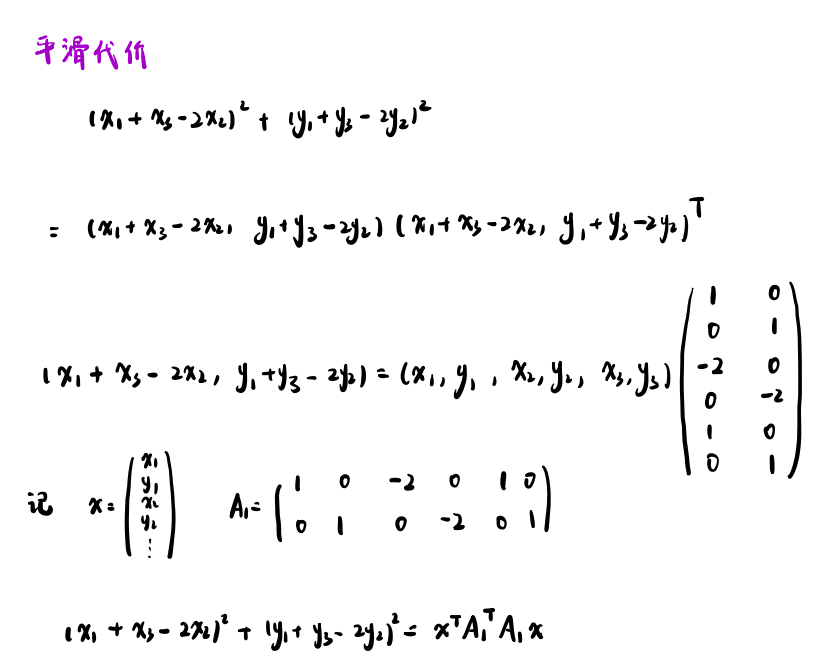
下面推广至n个点的情况:

基于优化方法是目前最主流、效果最好的一类方法。其核心思想是将平滑问题定义为一个数值优化问题,通过最小化一个精心设计的目标函数来求解。
基本框架:
我们有一系列原始路径点 (x_i, y_i),我们希望找到一组新的点 (x_i', y_i'),使得目标函数 J 最小。
目标函数 J 通常由几个部分组成:
平滑度代价:惩罚路径的弯曲程度。常用的是路径点的二阶导(加速度) 或三阶导(加加速度) 的平方和。
Cost_smooth = Σ ( (x_{i-1} - 2x_i + x_{i+1})^2 + (y_{i-1} - 2y_i + y_{i+1})^2 )这个项最小化意味着路径尽可能是一条直线。
几何相似性代价:惩罚平滑后的路径点偏离原始路径点太远,保证平滑后的路径不会“跑偏”。
Cost_length = Σ ( (x_i' - x_i)^2 + (y_i' - y_i)^2 )这个项确保了平滑路径是原始路径的一个“精修版”,而不是一条完全不同的路径。
曲率代价:为了使路径更适合车辆行驶,可以直接在目标函数中加入对曲率的约束。
Cost_curvature = Σ (k_i)^2,其中k_i是点i处的曲率。曲率的计算比较复杂,通常用相邻线段夹角的近似值来代替。
最终的优化问题形式为:
Minimize J = w_smooth * Cost_smooth + w_length * Cost_length + w_curvature * Cost_curvature
其中 w_smooth, w_length, w_curvature 是权重系数,用于调整各项的重要性。
