机器学习(10)L1 与 L2 正则化详解
在机器学习中,我们常常会遇到“过拟合”的问题。也就是说,模型在训练数据上表现得非常好,但在测试数据上却一塌糊涂。为了防止模型“记住”数据而不是“学习”规律,我们通常会在训练时加入一种约束,让模型不要太复杂——这就是正则化(Regularization)。
这篇文章我们就来讲讲最常见的两种正则化:L1 正则化和 L2 正则化。
一、什么是正则化?
在训练模型时,我们希望代价函数 J(w,b) 越小越好。
比如在线性回归中,代价函数是均方误差(MSE):
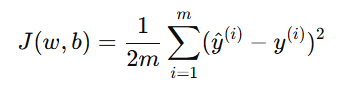
但如果我们只关注让误差变小,模型可能会把每个参数 wi 调得非常大,以尽量“贴合”所有样本。这样模型虽然在训练集上很准,但在新数据上容易失效。
于是我们在原有的代价函数后面加上一个“惩罚项”,限制参数不能太大:
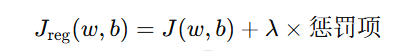
这里的 λ(lambda)叫做正则化系数,用于控制惩罚的强度。而“惩罚项”可以有不同的形式,于是就有了两种常见的正则化方式:L1 和 L2。
二、L1 正则化(Lasso Regularization)
L1 正则化的惩罚项是参数的绝对值之和:
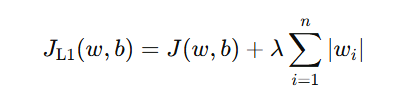
这意味着,参数 wi 越大,惩罚越强。L1 的一个特别之处在于:它会让某些参数直接变成 0。也就是说,它不仅能让模型更简单,还能起到特征选择的作用——把不重要的特征直接“删除”掉。
举个例子,假设我们在预测房价,特征包括:
房屋面积(x₁)
卧室数量(x₂)
是否靠近地铁(x₃)
如果“卧室数量”这个特征对预测影响很小,L1 正则化在训练时可能会让它的权重 w2 收敛为 0,从而自动忽略掉它。
这就是 L1 常被用于“稀疏模型(Sparse Model)”的原因。
三、L2 正则化(Ridge Regularization)
L2 正则化的惩罚项是参数平方和的一半:
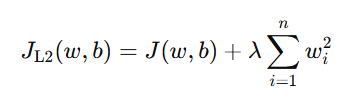
这里的惩罚项让模型在训练时“更平滑”,即:
不让某个参数特别大;
但也不会让某个参数直接变成 0。
因此,L2 正则化的效果是让所有权重都“更小”,但仍然保留在模型中。
举个例子,还是预测房价的场景,假设“卧室数量”的权重原本是 4,L2 正则化可能把它压缩到 1.2,而不是直接变成 0。这意味着模型仍然考虑了所有特征,只是弱化了它们的影响。
四、L1 与 L2 的主要区别
| 比较项 | L1 正则化(Lasso) | L2 正则化(Ridge) |
|---|---|---|
| 惩罚项形式 | 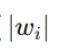 | |
| 几何形状 | 菱形约束区域 | 圆形约束区域 |
| 参数稀疏性 | 可以让部分参数=0(自动特征选择) | 参数变小但不为0 |
| 适合场景 | 需要筛选特征、希望模型简洁 | 特征较多且都重要、希望模型稳定 |
| 数学性质 | 不连续(尖点) | 连续光滑(易优化) |
五、为什么 L1 会让参数变成 0?
原因在于 L1 的惩罚项不是光滑的。
当你画出 L1 的几何约束(一个菱形)和损失函数的等高线(椭圆)时,两者的切点往往会出现在菱形的“尖角”上——也就是坐标轴上。
这意味着,某些权重 wi 恰好会被压到 0。
相比之下,L2 的约束是一个圆形,没有“尖角”,所以参数只会变小,不会直接为 0。
六、直观理解:从几何角度看区别
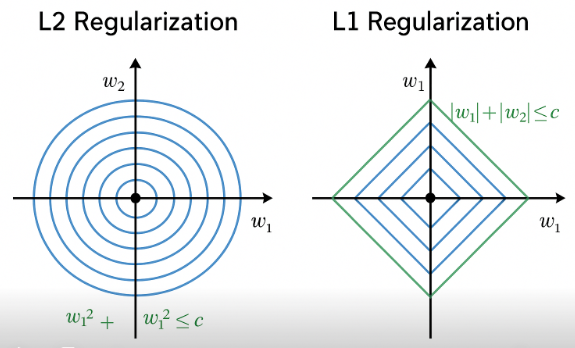
想象二维参数空间中:
L2 正则化:
约束区域是一个圆。椭圆形的代价函数等高线与圆相切时,最优点一般在圆弧上。
→ 所有参数都变小。L1 正则化:
约束区域是一个菱形。代价函数的等高线更容易与菱形的尖角相切。
→ 部分参数直接为 0。
七、实际应用建议
如果你希望模型自动挑选特征,用 L1 正则化(Lasso)。
如果你希望模型更稳定、抗噪音能力强,用 L2 正则化(Ridge)。
如果你想两者兼顾,可以使用 Elastic Net(弹性网络),它结合了 L1 和 L2 的优点:
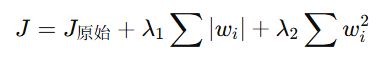
八、总结
正则化的核心目标是控制模型复杂度、避免过拟合。
L1 通过“让参数变成 0”简化模型;
L2 通过“让参数变小”让模型更平滑。
它们的差别虽然只是惩罚项形式不同,但带来的效果却截然不同。
