「用Python来学微积分」12. 无穷小量和无穷大量
引言
在微积分学习中,无穷小量是一个核心概念。它不仅是理解极限的基础,更是后续学习导数、积分等内容的桥梁。本文将通过理论讲解结合Python代码演示,帮助大家深入理解无穷小量的概念、性质及其比较方法。
一、无穷小量的基本概念
定义与记号
如果函数f(x)在x→x₀时的极限为0,即limx→x0f(x)=0\lim\limits_{x\to x_{0}}f(x)=0x→x0limf(x)=0,则称f(x)在x→x₀时是一个无穷小量,记作: f(x)=o(1)(x→x0)f(x)=o(1)(x\to x_{0})f(x)=o(1)(x→x0)
无穷大量的定义
如果1f(x)\frac{1}{f(x)}f(x)1在x→x₀时是无穷小量,则称f(x)在x→x₀时是无穷大量,记作limx→x0f(x)=∞\lim\limits_{x\to x_{0}}f(x)=\inftyx→x0limf(x)=∞。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.widgets import Slider# 中文显示
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False# 演示无穷小量:f(x) = x (当x→0时)
def plot_infinitesimal():fig, ax = plt.subplots(figsize=(10, 6))plt.subplots_adjust(bottom=0.25)x = np.linspace(-1, 1, 1000)f_x = xline, = plt.plot(x, f_x, label='f(x) = x')plt.axhline(y=0, color='r', linestyle='--', label='y=0')plt.xlabel('x')plt.ylabel('f(x)')plt.title('无穷小量示例: f(x) = x (x→0)')plt.legend()plt.grid(True)# 添加滑动条ax_scale = plt.axes([0.25, 0.1, 0.65, 0.03])scale_slider = Slider(ax_scale, '缩放', 0.01, 1.0, valinit=0.1)def update(val):scale = scale_slider.valx_min, x_max = -scale, scaleax.set_xlim(x_min, x_max)ax.set_ylim(x_min, x_max)fig.canvas.draw_idle()scale_slider.on_changed(update)plt.show()plot_infinitesimal()
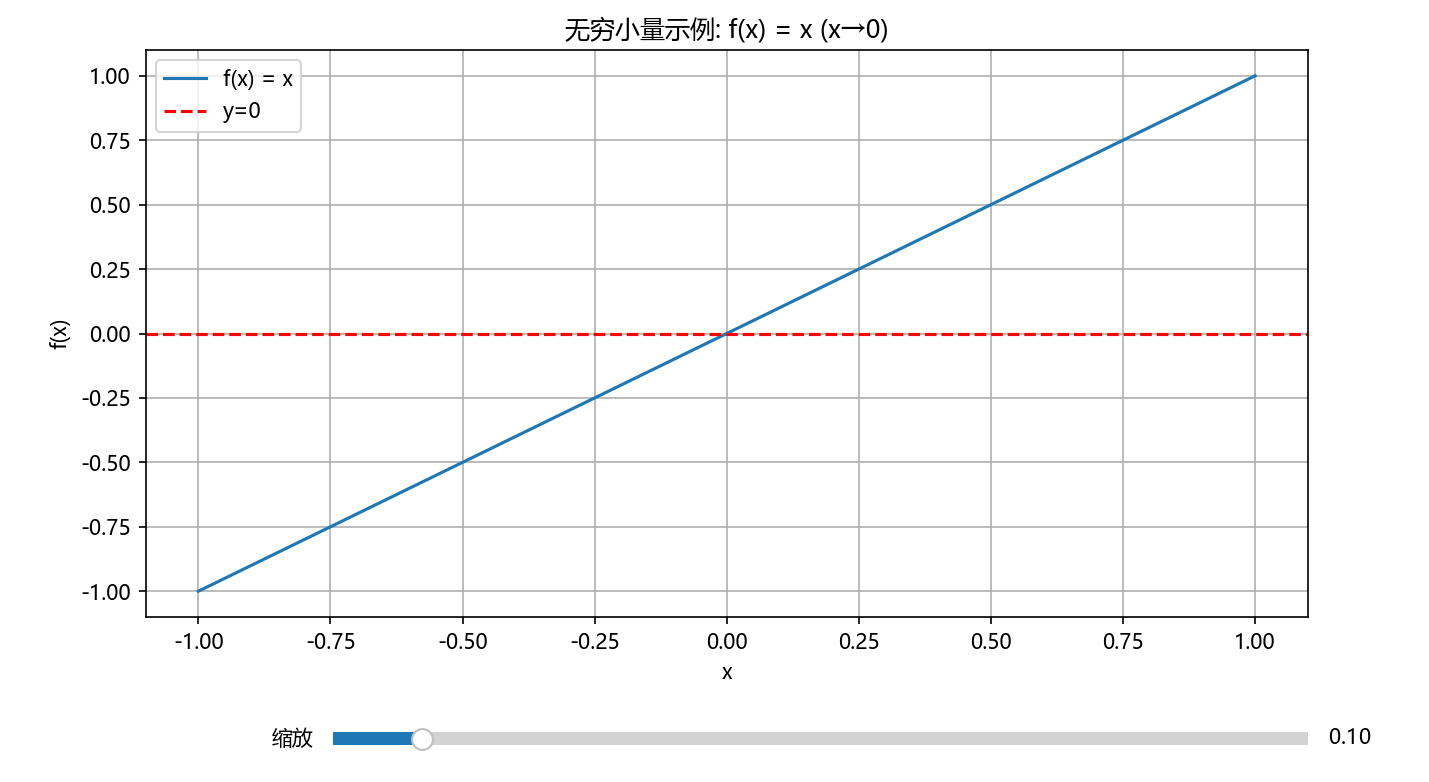
二、无穷小量的性质与运算
定理1:极限与无穷小的关系
limx→x0f(x)=A\lim\limits_{x\to x_{0}}f(x)=Ax→x0limf(x)=A ⇔ f(x)=A+g(x)f(x)=A+g(x)f(x)=A+g(x),其中limx→x0g(x)=0\lim\limits_{x\to x_{0}}g(x)=0x→x0limg(x)=0
定理2:有界函数与无穷小的乘积
在自变量的同一趋向下,有界函数与无穷小量的乘积仍是无穷小量。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.widgets import Slider# 中文显示
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False# 演示有界函数与无穷小的乘积:f(x) = x·sin(1/x) (x→0)
x = np.linspace(-0.1, 0.1, 1000)
f_x = x * np.sin(1/x)plt.figure(figsize=(10, 6))
plt.plot(x, f_x, label='f(x) = x·sin(1/x)')
plt.axhline(y=0, color='r', linestyle='--', label='y=0')
plt.xlim(-0.1, 0.1)
plt.ylim(-0.1, 0.1)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('有界函数与无穷小的乘积')
plt.legend()
plt.grid(True)
plt.show()
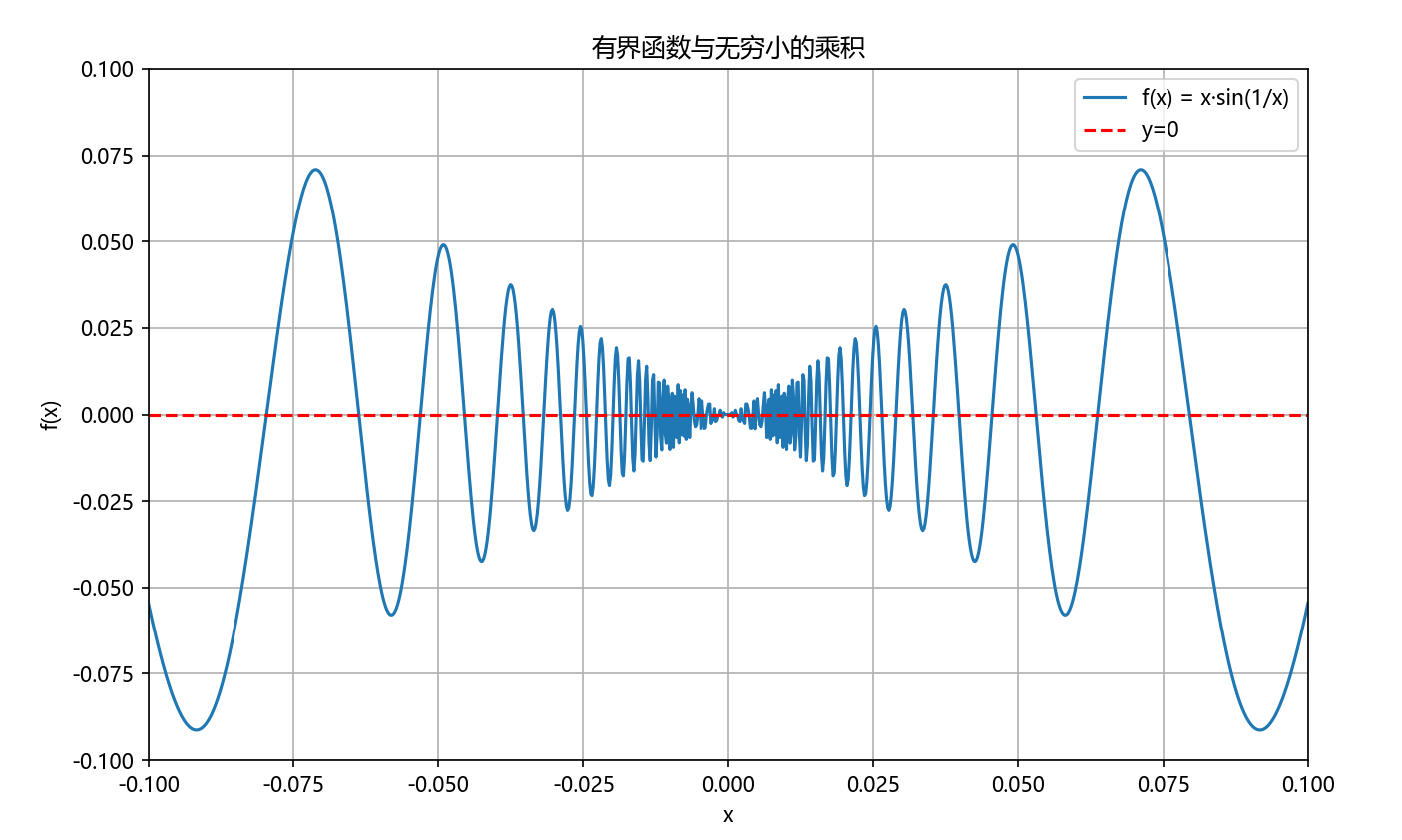
定理3:无穷小的运算性质
在自变量的同一趋向下,两个无穷小量的和、差、乘积仍是无穷小量。
三、无穷小量的比较
比较的定义
设limx→x0f(x)=0\lim\limits_{x\to x_{0}}f(x)=0x→x0limf(x)=0,limx→x0g(x)=0\lim\limits_{x\to x_{0}}g(x)=0x→x0limg(x)=0,如果limx→x0f(x)g(x)=c\lim\limits_{x\to x_{0}}\frac{f(x)}{g(x)}=cx→x0limg(x)f(x)=c,则:
- 当c=0时,f(x)是g(x)在x→x0x \to x_0x→x0时的高阶无穷小量:f(x)=o(g(x))(x→x0)f(x)=o(g(x))(x \to x_0)f(x)=o(g(x))(x→x0)
- 当c=1时,f(x)与g(x)在x→x0x \to x_0x→x0时是等价无穷小量:f(x)∼g(x)(x→x0)f(x)\sim g(x)(x \to x_0)f(x)∼g(x)(x→x0)
- 当c≠0且c≠1时,f(x)与g(x)在x→x0x \to x_0x→x0时是同阶无穷小量
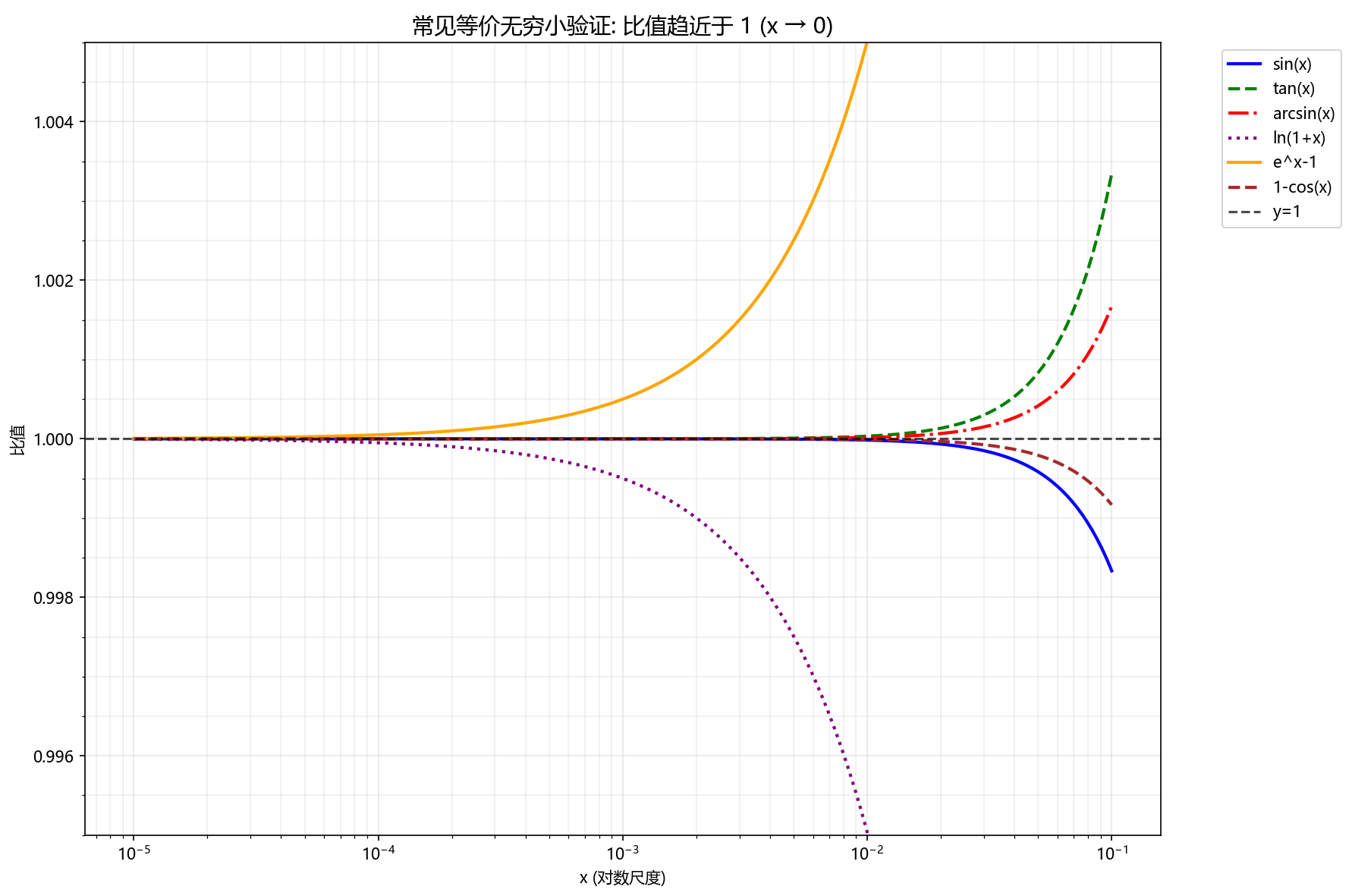
常见等价无穷小(x→0时)
- sinx∼x\sin x \sim xsinx∼x
- ln(1+x)∼x\ln(1+x) \sim xln(1+x)∼x
- ex−1∼xe^x - 1 \sim xex−1∼x
- 1−cosx∼12x21 - \cos x \sim \frac{1}{2}x^21−cosx∼21x2
- tanx∼x\tan x \sim xtanx∼x
import numpy as np
import matplotlib.pyplot as plt# 设置中文字体
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False# 生成更接近0的x值范围
x_values = np.array([0.1, 0.05, 0.01, 0.005, 0.001, 0.0005, 0.0001])print("等价无穷小验证 (x → 0)")
print("=" * 60)# 验证所有常见的等价无穷小
equivalents = [('sin(x) ~ x', lambda x: np.sin(x) / x),('tan(x) ~ x', lambda x: np.tan(x) / x),('arcsin(x) ~ x', lambda x: np.arcsin(x) / x),('ln(1+x) ~ x', lambda x: np.log(1 + x) / x),('e^x-1 ~ x', lambda x: (np.exp(x) - 1) / x),('1-cos(x) ~ x²/2', lambda x: (1 - np.cos(x)) / (0.5 * x**2))
]# 打印数值验证结果
for name, ratio_func in equivalents:print(f"\n{name}:")print(" x\t\t 比值")print("-" * 30)for x in x_values:try:ratio = ratio_func(x)print(f" {x:.6f}\t {ratio:.8f}")except:print(f" {x:.6f}\t 计算错误")# 可视化:使用更接近0的x范围
plt.figure(figsize=(12, 8))# 生成用于绘图的x值(更小的范围,更接近0)
x_plot = np.logspace(-5, -1, 200) # 从10^-5到10^-1# 定义颜色和线型(与图片保持一致)
colors = ['blue', 'green', 'red', 'purple', 'orange', 'brown']
linestyles = ['-', '--', '-.', ':', '-', '--']
linewidths = [2, 2, 2, 2, 2, 2]# 计算并绘制所有比值曲线
for i, (name, ratio_func) in enumerate(equivalents):ratio_values = []for x in x_plot:try:ratio_values.append(ratio_func(x))except:ratio_values.append(np.nan)ratio_values = np.array(ratio_values)plt.semilogx(x_plot, ratio_values, color=colors[i], linestyle=linestyles[i],linewidth=linewidths[i], label=name.split('~')[0].strip())# 添加参考线
plt.axhline(y=1, color='black', linestyle='--', alpha=0.7, label='y=1')plt.xlabel('x (对数尺度)')
plt.ylabel('比值')
plt.title('常见等价无穷小验证: 比值趋近于 1 (x → 0)', fontsize=14)
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
plt.grid(True, alpha=0.3)# 设置更精细的y轴范围,更好地显示趋近过程
plt.ylim(0.995, 1.005)# 添加次要网格线
plt.minorticks_on()
plt.grid(True, which='minor', alpha=0.2)plt.tight_layout()
plt.show()# 在极小的x值下验证
print("\n" + "=" * 60)
print("在极小的 x 值下的比值验证:")
print("=" * 60)tiny_x_values = [1e-3, 1e-4, 1e-5, 1e-6]
for x in tiny_x_values:print(f"\nx = {x:.0e}:")for name, ratio_func in equivalents:try:ratio = ratio_func(x)print(f" {name.split('~')[0].strip():12} 比值 = {ratio:.10f}")except:print(f" {name.split('~')[0].strip():12} 计算错误")
四、等价无穷小的应用
定理4:等价无穷小替换
在极限运算中,乘法因子和除法因子可以用它们在同一个极限过程下的等价无穷小代替。
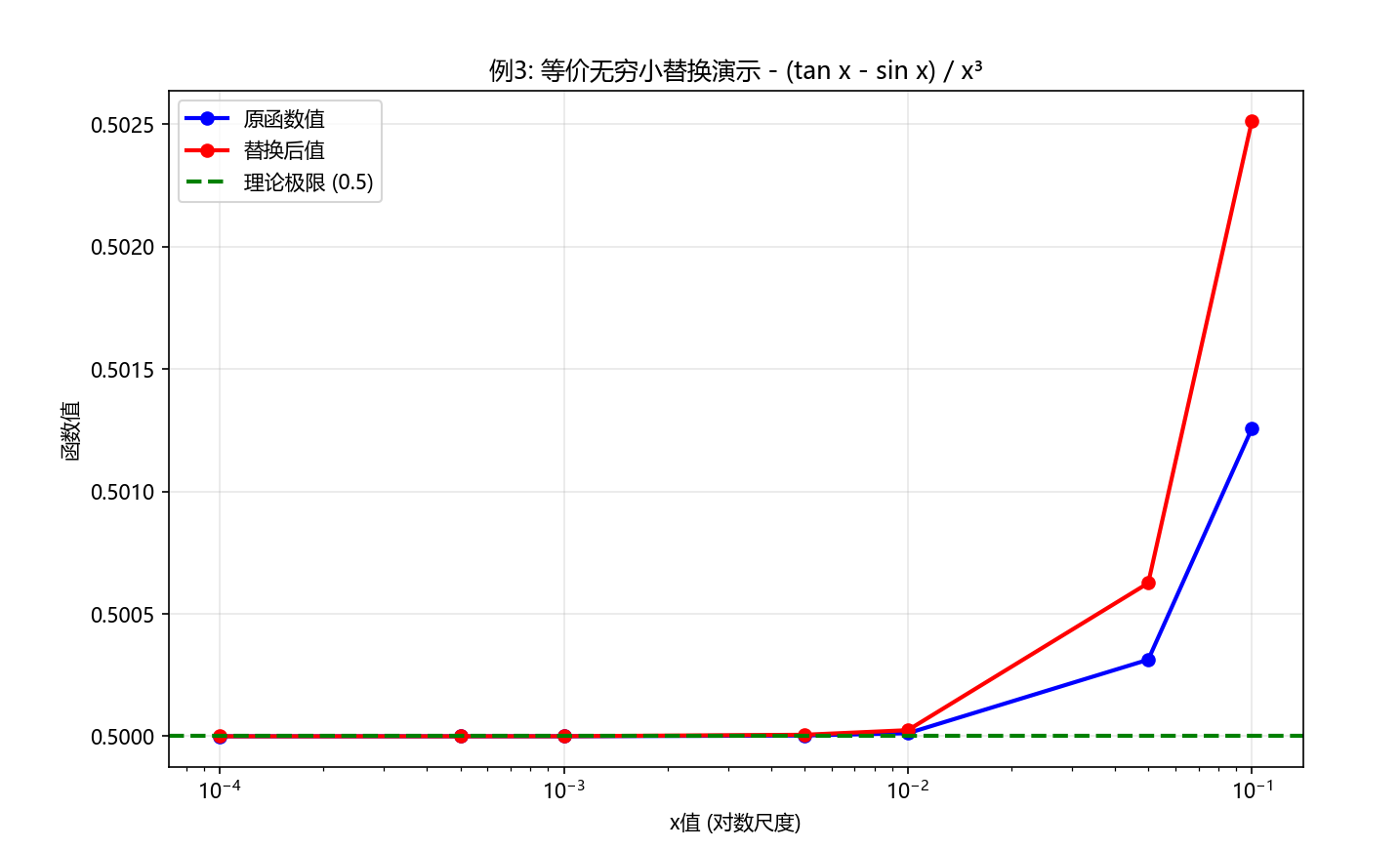
案例: 求极限 lim x → 0 tan x − sin x x 3 \lim \limits_{x \to 0}\frac{\tan x -\sin x}{x^3} x→0limx3tanx−sinx
import numpy as np
import matplotlib.pyplot as plt
from math import sin, cos, tan# 设置中文字体
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False# 例3: 计算 lim(x→0) (tan x - sin x) / x³
def example_3():# 生成趋近于0的x值x_values = np.array([0.1, 0.05, 0.01, 0.005, 0.001, 0.0005, 0.0001])print("例3: 计算 lim(x→0) (tan x - sin x) / x³")print("=" * 50)# 直接计算原函数值original_values = []for x in x_values:numerator = tan(x) - sin(x)denominator = x**3value = numerator / denominator if denominator != 0 else float('nan')original_values.append(value)print(f"x = {x:.5f}, 原函数值 = {value:.8f}")# 使用等价无穷小替换计算print("\n使用等价无穷小替换:")equivalent_values = []for x in x_values:# 使用替换: sin x ~ x, 1-cos x ~ x²/2# 原式 = (1-cos x)·sin x / (x³ cos x) ~ (x²/2)·x / (x³ cos x) = 1/(2 cos x)value = 1 / (2 * cos(x))equivalent_values.append(value)print(f"x = {x:.5f}, 替换后值 = {value:.8f}")# 理论极限值theoretical_limit = 0.5print(f"\n理论极限值 = {theoretical_limit}")# 可视化比较plt.figure(figsize=(10, 6))# 绘制原函数值plt.semilogx(x_values, original_values, 'bo-', linewidth=2, markersize=6, label='原函数值')# 绘制替换后值plt.semilogx(x_values, equivalent_values, 'ro-', linewidth=2, markersize=6, label='替换后值')# 绘制理论极限值plt.axhline(y=theoretical_limit, color='green', linestyle='--', linewidth=2, label='理论极限 (0.5)')plt.xlabel('x值 (对数尺度)')plt.ylabel('函数值')plt.title('例3: 等价无穷小替换演示 - (tan x - sin x) / x³')plt.legend()plt.grid(True, alpha=0.3)plt.show()# 运行示例
example_3()
运行结果:
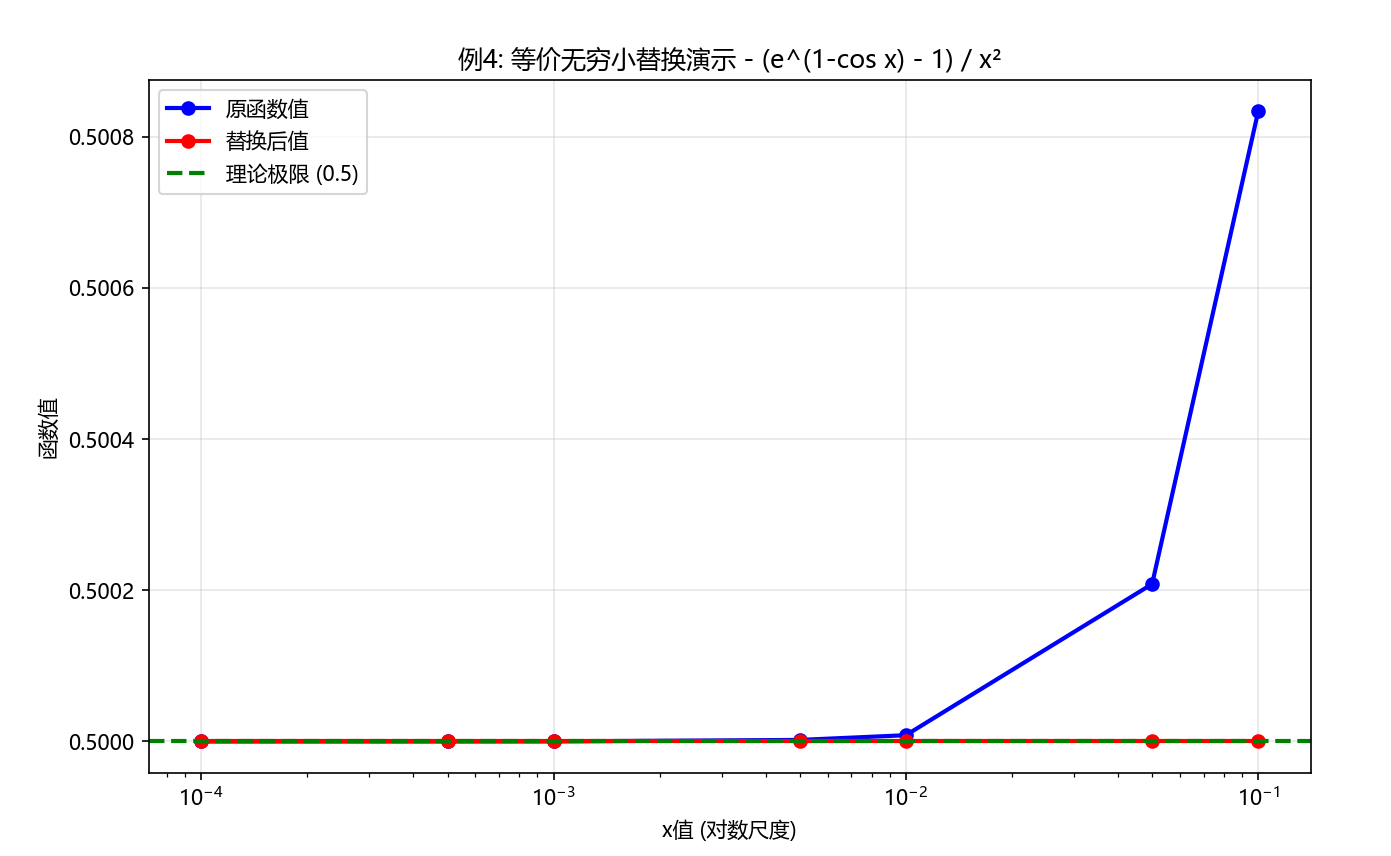
案例: 求极限 lim x → 0 e 1 − cos x − 1 x 2 \lim \limits_{x \to 0}\frac{e^{1-\cos x}-1}{x^2} x→0limx2e1−cosx−1
import numpy as np
import matplotlib.pyplot as plt
from math import sin, cos, tan# 设置中文字体
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False# 例4: 计算 lim(x→0) (e^(1-cos x) - 1) / x²
def example_4():from math import exp# 生成趋近于0的x值x_values = np.array([0.1, 0.05, 0.01, 0.005, 0.001, 0.0005, 0.0001])print("\n例4: 计算 lim(x→0) (e^(1-cos x) - 1) / x²")print("=" * 50)# 直接计算原函数值original_values = []for x in x_values:numerator = exp(1 - cos(x)) - 1denominator = x**2value = numerator / denominator if denominator != 0 else float('nan')original_values.append(value)print(f"x = {x:.5f}, 原函数值 = {value:.8f}")# 使用等价无穷小替换计算print("\n使用等价无穷小替换:")equivalent_values = []for x in x_values:# 使用替换: e^u - 1 ~ u (当u→0), 1-cos x ~ x²/2# 所以 e^(1-cos x) - 1 ~ 1-cos x ~ x²/2# 原式 ~ (x²/2) / x² = 1/2value = 0.5equivalent_values.append(value)print(f"x = {x:.5f}, 替换后值 = {value:.8f}")# 理论极限值theoretical_limit = 0.5print(f"\n理论极限值 = {theoretical_limit}")# 可视化比较plt.figure(figsize=(10, 6))# 绘制原函数值plt.semilogx(x_values, original_values, 'bo-', linewidth=2, markersize=6, label='原函数值')# 绘制替换后值plt.semilogx(x_values, equivalent_values, 'ro-', linewidth=2, markersize=6, label='替换后值')# 绘制理论极限值plt.axhline(y=theoretical_limit, color='green', linestyle='--', linewidth=2, label='理论极限 (0.5)')plt.xlabel('x值 (对数尺度)')plt.ylabel('函数值')plt.title('例4: 等价无穷小替换演示 - (e^(1-cos x) - 1) / x²')plt.legend()plt.grid(True, alpha=0.3)plt.show()# 运行示例
example_4()
运行结果:
五、总结
通过本文的学习,我们掌握了:
- 无穷小量的基本概念:极限为零的函数变量
- 无穷小量的性质:有界函数与无穷小的乘积、无穷小之间的运算
- 无穷小的比较方法:高阶、同阶、等价无穷小的定义和判断
- 等价无穷小的应用:在极限计算中的替换技巧
Python代码演示帮助我们直观理解这些抽象概念,特别是通过交互式可视化和数值实验验证理论结果。掌握无穷小量的比较方法对于后续学习导数、微分、泰勒展开等高级微积分概念至关重要。
在实际应用中,等价无穷小替换是计算复杂极限的强大工具,但需要注意替换的适用条件(只能是乘法因子或除法因子)。通过不断练习,你将能熟练运用这些技巧解决各类微积分问题。
延伸思考
- 如何在编程中避免无穷小量带来的数值不稳定问题?
- 除了微积分,无穷小量在机器学习、物理建模等领域还有哪些应用?
- 如何将无穷小的概念扩展到多维空间?
希望这篇结合了理论和Python实践的文章能帮助你深入理解无穷小量这一微积分核心概念!
参考资料:
- 扈志明,《微积分》,高等教育出版社
欢迎点赞、收藏、评论,您的支持是我持续创作的最大动力!如有任何疑问,欢迎在评论区提出,我会尽快解答。。
