【Dataset】如何高效处理海量数据并从中智能筛选出有代表性的样本？

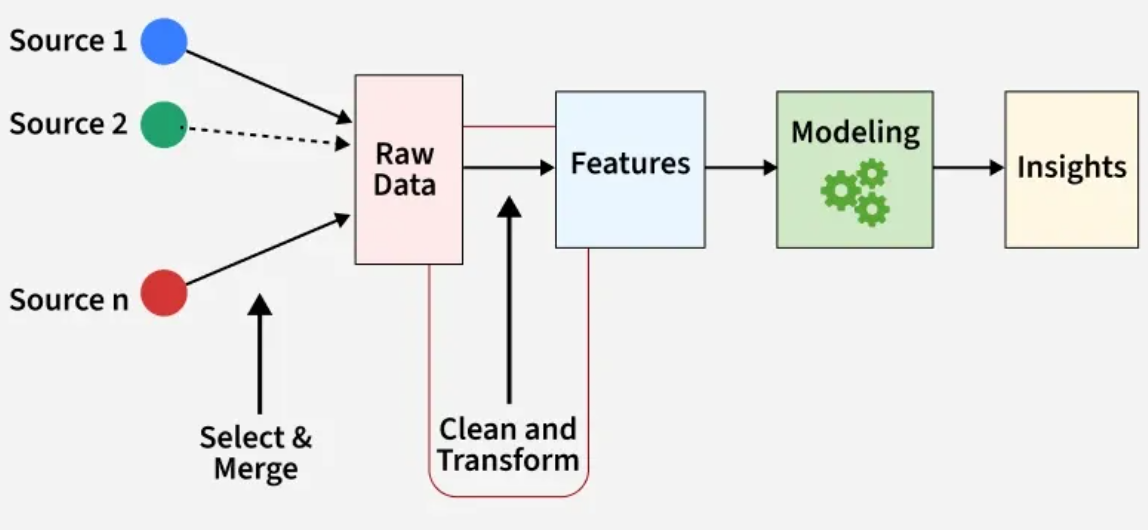
数据和特征决定了机器学习的上限，而模型和算法只是逼近这个上限而已，所以数据特征是否全面，数据量是否足够对于算法来说是非常重要的。

本文要谈论的：从海量未标注数据中 高效提取特征、发现结构，并 基于多目标价值评估进行有策略的样本采样，服务于主动学习、异常检测、数据压缩或 高质量数据集构建 等任务。

海量数据构建高质量数据集

首先得有海量数据昂。

四步走战略：原始信号 → 特征提取 → （可选）降维 → 聚类/采样

Step 1. 流式批特征提取

原始 .h5 文件包含的是 高维、原始、难以直接使用的信号数据（如音频波形、图像像素）；经过 流式批特征提取 后，新 .h5 文件中存储的是 低维、紧凑、语义丰富的 embedding 向量（如 512 维特征），可以直接用于聚类、降维、采样等下游任务，且整个过程 内存友好、只需遍历原始数据一次。

这一步希望完成以下任务：从一个 超大的 HDF5 文件 中读取原始数据 → 提取特征（如通过 CNN、手工特征或统计量）→ 将提取出的特征保存为另一个文件（如新的 HDF5 或 numpy 格式），全程仅遍历原始数据一次，且 不耗尽内存（内存不足以一次性加载所有数据）。

适用场景举例：

• 语音识别：从百万条语音中提取 Wav2Vec 特征用于 聚类
• 医学影像：从 MRI slice 序列中提取 CNN embedding
• 工业传感器：对振动信号做 autoencoder 编码用于 故障检测
• 行为识别：从 IMU 数据中提取时空特征用于 用户分群

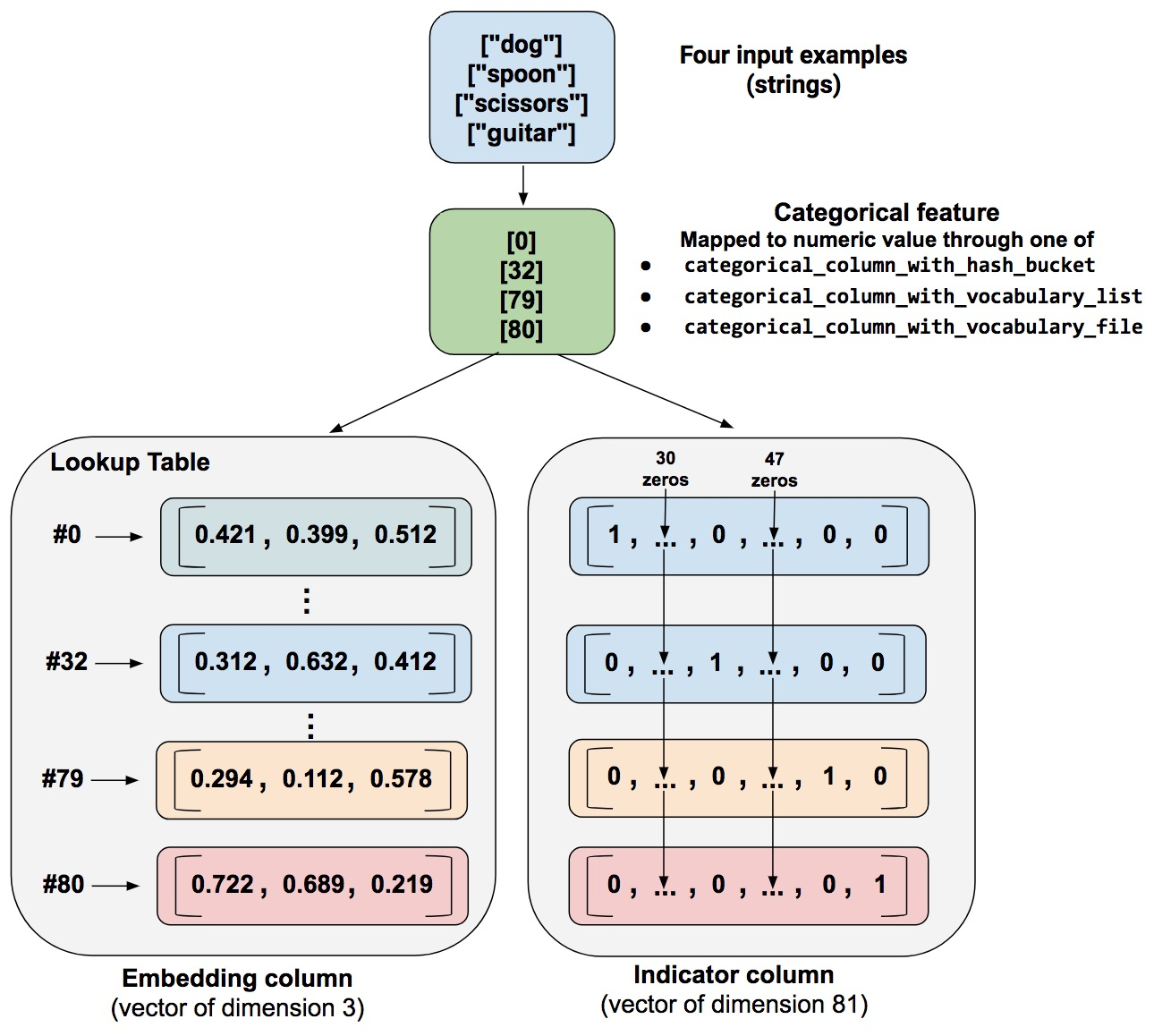
除了数值数据，对于分类、 字符串数据，不是简单的将其转换为数值型，而是将其 转换为一个向量 embedding。
图源文章 Introducing TensorFlow Feature Columns

接下来是 具体实现步骤，假设你有一个 HDF5 文件 raw_data.h5，其中包含：

with h5py.File('raw_data.h5', 'r') as f:print(f.keys())  # ['signals', 'labels', 'metadata']print(f['signals'].shape)  # (1_000_000, 128, 6) → 百万段信号，每段 128 时间步，6 通道

我们要从中提取特征，比如用一个神经网络将 (128,6) 映射为 (512,) 的 embedding。

Step 1: 定义特征提取模型

import torch
import torch.nn as nnclass SimpleEncoder(nn.Module):def __init__(self):super().__init__()self.conv = nn.Sequential(nn.Conv1d(6, 32, kernel_size=3),nn.ReLU(),nn.AdaptiveAvgPool1d(32))self.fc = nn.Linear(32*32, 512)def forward(self, x):# x shape: (B, T, C) → (B, C, T)x = x.transpose(1, 2)x = self.conv(x)x = x.flatten(start_dim=1)return self.fc(x)

假设已经训练好了，加载模型并置于设备上：

device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model = SimpleEncoder().to(device)
model.eval()  # 推理模式

Step 2: 设置输入和输出路径，创建输出 HDF5 文件

import h5py
import numpy as npinput_path = 'raw_data.h5'
output_path = 'enhanced_data.h5'  # 如果只需要保存提取的 feature, 则保存为 'features.h5'feat_dim = 512  # 输出特征维度
chunk_size = 256  # 每次处理 256 条# 在外层同时管理两个文件：从旧文件读取 并 写入新文件
with h5py.File(input_path, 'r') as infile, h5py.File(output_path, 'w') as outfile:N = infile['signals'].shape[0]raw_data = infile['signals']  # ← 只是一个“指针”，不是数组！# Step 1: 复制原始数据（按需保留）infile.copy('signals', outfile)   # ← 保留 signalsif 'labels' in infile:outfile['labels'] = infile['labels'][:]  # 保留 labelsif 'metadata' in infile:infile.copy('metadata', outfile)         # 递归复制 metadata# Step 2: 创建新的 features 数据集features_dset = outfile.create_dataset('features',shape=(N, feat_dim),dtype='float32',chunks=True,compression='gzip')# Step 3: 流式提取并写入 featuresfor i in range(0, N, chunk_size):end_idx = min(i + chunk_size, N)batch_x = raw_data[i:end_idx]  # shape: (chunk_size, T, C)  ← 此刻才从硬盘读取这 256 条数据batch_tensor = torch.tensor(batch_x, dtype=torch.float32).to(device)  # 转为 tensor 并移到 GPUwith torch.no_grad():   # 前向传播，获取特征features = model(batch_tensor)  # shape: (B, 512)features_dset[i:end_idx] = features.cpu().numpy()  # 写回硬盘# 打印进度if i % (chunk_size * 10) == 0:print(f"Processed {i}/{N} samples")print("✅ All data (signals, labels, metadata, features) saved.")

关键点：infile['signals'] 并不加载数据！

raw_data 是一个 h5py._hl.dataset.Dataset 对象，它 指向磁盘上的数据块，只有切片访问时才真正读入内存。

在这个例子中：

• 原始 raw_data.h5 包含的是 百万条原始 (128,6) 时间序列信号及其标签与元数据；
• 处理后的 features.h5 包含的是对应的 (512,) embedding 特征向量，并保留了原有的 signals、labels 和 metadata，实现了 从“原始观测”到“语义表示”的转换，支持后续高效、低资源消耗的分析任务。

enhanced_data.h5
├── signals      → 原始信号 (1_000_000, 128, 6)
├── labels       → 标签 (1_000_000,)
├── metadata     → 元数据 Group（subject_id, session_time...）
└── features     → 新提取的 embedding (1_000_000, 512)

• 用 features 做 聚类 / 可视化 / 训练模型
• 用 signals 做信号分析 / 检查原始波形
• 用 labels 和 metadata 做分组统计、回溯分析

整个过程仅遍历原始数据一次，使用 批处理 和 HDF5 的懒加载机制 保证内存友好，是一种 工业级的大规模特征工程标准做法。

Step 2. Incremental PCA（在线降维） + MiniBatchKMeans（大规模聚类）

这套组合是专为大规模、高维、无法一次性加载进内存的数据集设计的 在线学习 方案。

• 普通方法 PCA.fit(features) 需要将全部数据载入内存 → OOM（Out of Memory），解决方法：使用 Incremental PCA
• 标准 K-Means 每次迭代遍历全量数据 → 太慢，解决方法：使用 MiniBatchKMeans

📌 类比：就像一边看书一边做笔记总结，而不是等看完整本书才开始写摘要。

Incremental PCA（增量主成分分析）

Incremental PCA 是标准 PCA 的在线版本。不要求一次性输入所有数据，支持 partial_fit(X_batch) 方法，逐批次更新主成分方向，最终可将高维特征投影到低维空间（如 512 → 64）。这需要两遍扫描，

• 第一遍扫描（First Pass）：学习 PCA 的主成分方向（即“哪些维度最重要”）
• 第二遍扫描（Second Pass）：应用这些主成分，把原始数据投 影到低维空间，得到最终的降维结果。

from sklearn.decomposition import IncrementalPCAipca = IncrementalPCA(n_components=64, batch_size=256)
with h5py.File('features.h5', 'r') as f:X = f['features']N = len(X)chunk_size = 256for i in range(0, N, chunk_size):batch = X[i:i+chunk_size]ipca.partial_fit(batch)  # ← 增量学习主成分print("✅ IPCA training completed.")

由于 IncrementalPCA 不支持直接对 HDF5 dataset 转换，需要再次流式应用：

with h5py.File('features.h5', 'r') as f, h5py.File('reduced_features.h5', 'w') as outf:X = f['features']N = len(X)chunk_size = 256dset = outf.create_dataset('embedding_64d', (N, 64), dtype='float32')  # 创建输出 datasetfor i in range(0, N, chunk_size):batch = X[i:i+chunk_size]reduced = ipca.transform(batch)  # ← 应用降维dset[i:i+chunk_size] = reducedprint("✅ All data transformed to 64D.")

假设 embedding 是由两个主要模式驱动的：是否发生快速上升（电压突变）、是否出现震荡衰减。

第一遍扫描 的目标就是让 PCA 发现这两个“潜在因子”作为主成分方向。一旦发现，第二遍扫描 就可以 用这两个方向来描述每条轨迹。

MiniBatchKMeans（小批量 K-Means）

这是从 降维后的语义空间 走向 结构发现 的关键一步。

K-Means 的变体，每次只用一个小 batch 更新聚类中心。使用梯度近似方式更新 centroid，速度快、内存省。

from sklearn.cluster import MiniBatchKMeans
import numpy as npkmeans = MiniBatchKMeans(n_clusters=100, batch_size=256, max_iter=100, random_state=42)
with h5py.File('features.h5', 'r') as f:X = f['features']N = len(X)chunk_size = 256# 第一次调用需要初始化init_batch = X[:kmeans.batch_size]kmeans.fit(init_batch)  # 先 fit 初始化 centroids# 然后用 partial_fit 增量更新for i in range(0, N, chunk_size):batch = X[i:i+chunk_size]kmeans.partial_fit(batch)print("✅ MiniBatchKMeans clustering completed.")

💡 注意：partial_fit 会 持续更新模型，包括 centroid 和 inertia。

每次调用 partial_fit，MiniBatchKMeans 执行以下步骤：

1. 随机选择一部分样本作为“新观测”
2. 将每个样本分配给最近的 cluster center
3. 以滑动平均方式更新该 center：
   $${\mathbf{c}}_j\leftarrow (1-\eta )\cdot {\mathbf{c}}_j+\eta \cdot \frac{1}{|B_j|}\sum _{i\in B_j}{\mathbf{x}}_i$$
   其中：$\eta$ 是学习率，$B_j$ 是当前 batch 中属于第 j 个 cluster 的样本。

训练完成后，可以获取每个样本的 cluster label（需 再次流式预测），

with h5py.File('features.h5', 'r') as f, h5py.File('clusters.h5', 'w') as outf:X = f['features']N = len(X)chunk_size = 256dset = outf.create_dataset('cluster_id', (N,), dtype='int32')for i in range(0, N, chunk_size):batch = X[i:i+chunk_size]preds = kmeans.predict(batch)dset[i:i+chunk_size] = predsprint("✅ Cluster assignments saved.")

查看聚类中心：

centers = kmeans.cluster_centers_  # shape: (100, 512)

可用于后续“查找最典型样本”或“生成合成样本”。

直接在原始空间聚类，保留更多细节不损失信息，但需要更大 batch size 和更多迭代，适用于确信 高维结构很重要的场景（如细粒度类别区分）。

聚类本身只依赖低维 embedding，所有 scoring 都是事后分析，不影响聚类结果。

如何评估聚类质量？（无监督指标）

• Inertia：样本到其 cluster 中心的距离平方和，越小越好。
• Silhouette Score：衡量簇间分离度（可对 batch 估算），越大越好。

Step 3. Cluster 内分层采样（Stratified Sampling within Clusters）并使用概率抽样（softmax temperature）

这一步的目标是：在每一个 cluster 中，有策略地选出最具代表性的 k 个样本，用于后续人工标注、异常分析或 构建高质量子集。 每个 cluster 是一层，每层独立采样，确保覆盖所有类型。

举个例子，可以为每个样本计算下面这些 score，并加权组合成一个 综合得分。

• Stability Score（稳定性）：衡量一个样本是否 长期稳定 属于这个 cluster。高 stability = 长期一致归属某类 → 典型代表；低 stability = 经常被分到不同 cluster → 边界/模糊样本。

  方法：使用 余弦相似度 到 cluster center，

  from sklearn.metrics.pairwise import cosine_similaritysimilarity = cosine_similarity(X_cluster, center.reshape(1, -1)).flatten()
  stability_score = similarity  # 越接近 center 越稳定
  

  Stability 的用途

  • 构建基准数据集：选 high-stability 样本作为“标准工况”；
  • 数据清洗：low-stability 可能是标签错误或噪声；
  • 工况分类：每个 cluster 中挑最稳定的做 prototype。

• Novelty Score（新颖性）：衡量一个样本是否 “与众不同” —— 可能是异常或罕见模式。定义是样本到其所属 cluster center 的距离，距离越远，表示该样本越“偏离典型模式”，可能是异常、边界样本或新行为。

  方法：使用 欧氏距离 到 cluster center，

  distances = np.linalg.norm(X_cluster - center, axis=1)
  novelty_score = distances  # 距离越远越“新”
  

• Energy Score（能量强度）：适用于电流/电压信号，反映事件的 显著程度。

  方法：计算 原始信号的能量（如 RMS），

  # 取对应 cluster 的原始信号
  raw_cluster = raw_signals[mask]  # (M, 32, 3)# 计算总 RMS 能量（可按通道加权）
  rms = np.sqrt(np.mean(raw_cluster ** 2, axis=(1, 2)))  # (M,)
  energy_score = (rms - rms.min()) / (rms.max() - rms.min() + 1e-8)  # 归一化
  

然后将多个 score 加权融合：

 # 归一化所有 score 到 [0,1]
def normalize(x):return (x - x.min()) / (x.max() - x.min() + 1e-8)s_scores = normalize(stability_score)      # 高分：典型
n_scores = normalize(novelty_score)        # 高分：异常
e_scores = normalize(energy_score)         # 高分：强信号# 加权求和（注意符号  正向：越高越好；负向：越低越好）
composite_score = (weights['stability'] * s_scores + weights['novelty'] * n_scores + weights['energy'] * e_scores)

使用 Softmax + Temperature 进行概率抽样是要引入可控的随机性。不能直接取 top-k，那样会失去多样性。

# 使用 softmax 转换为概率分布
probabilities = softmax(composite_score / temperature)# 温度控制探索 vs 利用
# - temperature >> 1: 更均匀，探索性强
# - temperature << 1: 集中在高分样本，利用性强# 概率化抽样（不放回）
selected_local_idx = np.random.choice(np.arange(M),size=k,replace=False,p=probabilities
)# 映射回全局 index
selected_global_idx = indices[selected_local_idx]return selected_global_idx.tolist()

• T = 0.1：几乎只选最高分样本，挑选最典型代表
• T = 1.0：平衡选择，通用推荐
• T = 5.0：接近均匀随机，探索未知、防偏见
• T → ∞：完全随机，纯探索模式
• T → 0：总是选最大值，贪心策略

对所有 cluster 执行分层采样：

all_selected = []for cid in np.unique(cluster_labels):selected_in_cluster = cluster_internal_sampling(features=features,cluster_labels=cluster_labels,cluster_centers=cluster_centers,target_cluster=cid,k=10,  # 每簇选 10 个temperature=1.5,weights={'stability': 0.5,'novelty': 1.0,   # 更关注异常'energy': 0.8     # 偏好强信号})all_selected.extend(selected_in_cluster)print(f"Total selected: {len(all_selected)} samples")

不要只挑最好的，也不要随便乱挑；而要在一个有意义的群体内部，按照多维价值评分，用带温度的概率方式智能抽取。

举例子总结

举个例子，面对一个 超大规模时间序列数据集（$N=2000万$ 样本），每个样本是 $C=3$ 通道 × $T=32$ 时间步 的物理信号（电流、电压、位置），该如何设计特征提取与降维策略？

直接使用原始 (3,32)，存在问题如 缺乏语义表达力（原始波形变化大，但语义可能相似，如相位偏移），信息冗余等。

推荐用轻量神经网络 提取 embedding，如 1D CNN 或 Transformer Encoder（小规模）。

关键矛盾点：“我想用 Transformer Encoder 提取特征，但它需要训练 —— 而我没有标注数据。”

Transformer 编码器

数据是：(B, C=3, T=32) 的时间序列（电流、电压、位置），每条是一个短时序。设计一个 无需标签也能使用 的 Transformer 编码器，想用一个 Transformer Encoder 将每条轨迹压缩成一个 全局语义 embedding（如 (B, T, C) -> (B, dim)），以便后续：聚类分析或分布可视化等。

第一步，正弦位置编码，为每个时间步生成一个唯一的、基于正弦和余弦函数的“位置 ID”，并将其加到输入特征上，从而使 Transformer 能够感知 时间顺序。

class PositionalEncoding(nn.Module):def __init__(self, d_model, max_len=512):super().__init__()pe = torch.zeros(max_len, d_model)   # (max_len, d_model)pos = torch.arange(0, max_len).unsqueeze(1).float()   # [0, 1, 2, ..., max_len-1]  -> (max_len, 1)div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))  # [0, 2, 4, ..., d_model-2] pe[:, 0::2] = torch.sin(pos * div_term)  # 偶数列：sinpe[:, 1::2] = torch.cos(pos * div_term)  # 奇数列：cosself.register_buffer('pe', pe.unsqueeze(0))  # (1, max_len, d_model)def forward(self, x):return x + self.pe[:, :x.size(1), :]

其中 (-math.log(10000.0) / d_model) 是一个常数，控制频率衰减速度。整体是
$$\text{div\_term[i]}=\exp \left(\frac{-2i\cdot \ln (10000)}{d_{model}}\right)=\frac{1}{10000^{2i/d_{model}}}$$

它实际上是在构造一组 指数衰减的频率，用于 生成不同波长的正弦波。假设 d_model=8，那么 div_term ≈ [1.0000, 0.1000, 0.0100, 0.0010]，是四个不同的缩放因子，对应低频到高频的振荡。

第二步，定义模型，

class TimeSeriesTransformerEncoder(nn.Module):def __init__(self, in_channels=3, d_model=64, n_layers=4, n_heads=4, dim_ff=256, dropout=0.1, max_len=128, cls_token=True):super().__init__()self.cls_token = cls_token　# 是否使用 `[CLS]` tokenself.in_proj = nn.Linear(in_channels, d_model)  #　线性投影层　(B, T, C=3) → (B, T, d_model=128)self.pos_enc = PositionalEncoding(d_model, max_len=max_len)  # 加了 PEencoder_layer = nn.TransformerEncoderLayer(d_model=d_model, nhead=n_heads, dim_feedforward=dim_ff, dropout=dropout, activation='gelu')self.encoder = nn.TransformerEncoder(encoder_layer, num_layers=n_layers)  # 堆叠 n_layers 层if cls_token:   # 类比 BERT, 最后取 [CLS] 的输出作为句子 embeddingself.cls = nn.Parameter(torch.randn(1, 1, d_model))   # 可学习的特殊 token (1,1,D) def forward(self, x):# x: (B, C, T)x = x.permute(0, 2, 1)  # -> (B, T, C)h = self.in_proj(x)  # (B, T, d_model)h = self.pos_enc(h)  # (B, T, d_model)if self.cls_token:B = h.shape[0]cls = self.cls.expand(B, -1, -1)  # (1,1,D) -> (B,1,D)h = torch.cat([cls, h], dim=1)  # (B, T+1, d_model)# transformer expects (S, N, E)h = h.permute(1, 0, 2)out = self.encoder(h)  # (S, N, E)out = out.permute(1, 0, 2)  # (B, S, E)if self.cls_token:emb = out[:, 0, :]  # (B, E)else:emb = out.mean(dim=1)return emb, out  # emb: global embedding, out: sequence embeddings

nn.TransformerEncoderLayer 是 PyTorch 内置的一个标准编码器层，包含：Multi-Head Self-Attention、Add & Norm、Feed-Forward Network (FFN)、Add & Norm。

encoder 是把 TransformerEncoderLayer 重复 n_layers 层，每一层都能捕捉更抽象的时间模式，第 1 层看局部相关性，第 4 层可能看到整个控制过程的动态规律。

torch.cat([cls, h], dim=1) 在 序列最前面插入 [CLS] token，目的是让 attention 机制有机会把所有信息汇总到 [CLS] 上，

原始:   [x₀, x₁, x₂, ..., x_{T-1}]        # (B, T, D)
插入后: [cls, x₀, x₁, ..., x_{T-1}]       # (B, T+1, D)

每一层中，[CLS] 都能 attend 到所有真实时间步，经过多层 Transformer 层传递，[CLS] 逐渐积累整条轨迹的语义信息。

最后，推荐使用 [CLS]，因为它是一个“主动聚合器”，而不是被动平均。

• 如果用了 [CLS]，取第一个 token 的输出：out[:, 0, :]，这就是要的 global embedding，代表整条轨迹的语义；
• 如果没用 [CLS]，对所有时间步平均池化：mean(dim=1)，也是一种 pooling 方式，但不如 [CLS] 灵活。

直观理解，假设训练好了这个 encoder，输入一条轨迹：电压突然上升 → 垂直位置快速抬升 → 然后震荡衰减 → 最终稳定在 z=0，Transformer 会通过 self-attention 发现这些因果关系：u[t] 和 z[t+Δt] 之间有强 attention weight，[CLS] token 学会总结：这是一次典型的快速响应控制，不同轨迹之间的相似性体现在 emb 的距离上。最终，相似的控制行为 → embedding 靠近，不同的控制策略 → embedding 分开。

每条样本映射为 64 维 compact embedding。为什么选择 64 维？ 比原始 (3,32)=96 维更紧凑、足够保留动态模式（上升沿、振荡、过冲等）、不至于过度压缩导致信息丢失。

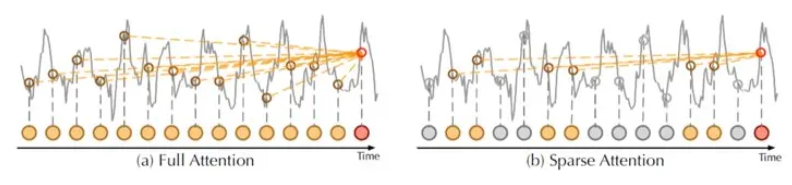
为了降低注意力层的二次复杂度，新 transformer 引入了 ProbSparse Attention 的概念。通过 让注意力层仅使用最重要的数据点来计算权重和概率，而不是全部数据点，ProbSparse 大幅缩短了计算注意力所需的时间。

自监督预训练（Self-Supervised Learning, SSL）

必须训练才能有效提取语义特征，但好消息是：你不需要人工标注！可以用无监督方式训练它。

使用 自监督预训练（Self-supervised Pretraining），即使没有标签，也可以通过以下方法“教会”Transformer 学习有用的时序模式。

一个 混合自监督训练策略，可以同时利用：

• 掩码重建：学习动态规律；
• 对比学习：学习不变表示。

方法	掩码重建（MAE）	对比学习（Contrastive）
输入	部分遮盖的序列	完整但增强的序列
输出	重建原始信号	embedding 之间的相对距离
学习方式	逐点预测	全局排序
关注点	局部一致性	全局语义相似性
是否需要 decoder	✅ 是	❌ 否
类比	填空题	多选题

掩码重建（Masked Autoencoder）

Masked Autoencoder（MAE）风格重建任务，原理：

• 随机遮盖一部分时间步（比如 mask 掉 75%）
• 让模型根据剩余部分重建原始信号
• 迫使模型学习上下文依赖和动态规律

# 伪代码示例
model.train()
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)for batch_x in dataloader:  # shape: (B, 32, 3)# 随机遮盖mask_ratio = 0.75mask = torch.rand(batch_x.shape[:2]) < mask_ratio  # (B, 32)masked_x = batch_x.clone()masked_x[mask] = 0.0  # 或填充均值# 前向传播得到 embeddinglatent = model.encoder(masked_x)  # 只取 [CLS]pred = model.decoder(latent)      # 解码回 (32,3)loss = F.mse_loss(pred, batch_x)optimizer.zero_grad()loss.backward()optimizer.step()

其中 mask = torch.rand(batch_x.shape[:2]) < mask_ratio # (B, T) 是在创建一个 布尔类型的随机掩码，用于标记哪些时间步将被遮盖（masked），即从输入中移除或置为零。

先生成一个形状为 (B, T) 的张量，假设 B=2, T=5，每个元素是从均匀分布 $U(0,1)$ 中随机采样的浮点数（范围在 0 到 1 之间），然后对每个元素判断是否小于 mask_ratio（比如 0.15），则 mask 就是，

[[0.34>0.15→False, 0.87>0.15→False, 0.12<0.15→True, 0.95>0.15→False, 0.46>0.15→False],[0.77>0.15→False, 0.03<0.15→True,  0.68>0.15→False, 0.21>0.15→False, 0.99>0.15→False]]

mask[b, t] == True → 第 b 条序列的第 t 个时间步 要被遮盖，mask[b, t] == False → 保留该时间步。

Masked Autoencoder (MAE)：重建被遮盖的部分。把 mask 的部分填充为 0， 然后把 masked_x 输入模型，让模型预测原始完整信号，损失函数 只计算被遮盖位置的误差。目标是训练模型理解时间序列的上下文依赖，学会“脑补”缺失部分。

模型会自动学会“从局部推测整体”，学到的是物理信号的内在结构。

对比学习（Contrastive Learning）

一句话理解 对比学习：让相似的东西靠近，不相似的东西远离。

• 相似的：同一条轨迹经过 不同增强（如加噪声、裁剪）→ 应该有相近的 embedding；
• 不相似的：完全不同控制行为的轨迹 → embedding 应该远。

模型通过这种方式学会 提取语义上有意义的特征，而不是记住原始波形。

对比学习是一种“自我监督”的方式，通过人为制造“同一事物的不同观察视角”，然后训练模型识别这些视角属于同一个实体。

• 在图像中：不同裁剪、旋转、颜色抖动 → 同一张图
• 在时间序列中：加噪声、缩放、裁剪 → 同一段控制过程

核心机制：正样本 vs 负样本

• 正样本对（Positive Pair）：语义相同但细节不同的样本，同一条轨迹 + 不同增强；
• 负样本对（Negative Pair）：完全不同的样本，其他 batch 中的任意轨迹。

z1 = augmentation(x)  # view 1: jitter + scale + crop
z2 = augmentation(x)  # view 2: 另一套随机参数

→ z1 和 z2 是一个正样本对！它们来自同一个原始轨迹 x，所以语义一致，但由于增强不同，外观略有差异。

def nt_xent_loss(z1, z2, temperature=0.2):z1 = F.normalize(z1, dim=1)  # L2 normalizez2 = F.normalize(z2, dim=1)batch_size = z1.size(0)z = torch.cat([z1, z2], dim=0)  # (2B, D)  拼接成大矩阵sim = torch.matmul(z, z.T) / temperature  # (2B, 2B)  计算相似度矩阵labels = torch.arange(batch_size, device=z.device)positives = torch.cat([torch.diag(sim, batch_size),   # z1[i] vs z2[i]torch.diag(sim, -batch_size)   # z2[i] vs z1[i]], dim=0)  # (2B,)# 构造分母（负样本求和）mask = (~torch.eye(2 * batch_size, dtype=torch.bool, device=z.device)).float()    # 排除自相似exp_sim = torch.exp(sim) * maskdenom = exp_sim.sum(dim=1)  # (2B,) 每行求和loss = -torch.log(torch.exp(positives) / (denom + 1e-12)).mean()return loss

这是 InfoNCE Loss 的一种简化实现，全称是 Normalized Temperature-scaled Cross Entropy Loss (NT-Xent)。

sim = torch.matmul(z, z.T) / temperature，sim[i,j] 表示第 i 个和第 j 个 embedding 的相似度，除以 temperature 控制分布锐度：温度小 → 差异放大；温度大 → 更平滑。

目标函数：InfoNCE / NT-Xent Loss（本质是分类），虽然叫“损失函数”，但它其实是在做一个分类任务：给定一个 query embedding（比如 z1[0]），从一堆候选中找出它的“配对项”（即 z2[0]）

$$\mathcal{L}=-\log \frac{\exp (\text{sim}(z_i,z_j)/\tau )}{{\sum }_{k=1}^{2B}{\mathbb{I}}_{k\ne i}\cdot \exp (\text{sim}(z_i,z_k)/\tau )}$$

其中：

• $z_i,z_j$：一对正样本（如 z1[0], z2[0]）
• $\text{sim}(a,b)=a^{T}b$：cosine 相似度
• $\tau$：temperature 温度超参（控制分布锐度）
• 分母包含所有其他样本（包括负样本）

负样本求和，即：
$${\text{denom}}_i=\sum _{j\ne i}\exp (\text{sim}[i,j])$$

📌 目标：最大化这个概率 → 让正样本得分远高于负样本

举个例子（B=2）

View	Embedding
v1_0	z1[0]
v2_0	z2[0] ← 正样本对
v1_1	z1[1]
v2_1	z2[1] ← 正样本对

目标：cos(z1[0], z2[0]) 要高，cos(z1[0], z1[1]), cos(z1[0], z2[1]) 要低。NT-Xent 自动完成这一优化。

拒绝神经网络，手工设计统计特征

不用神经网络，也能提取特征？

如果连训练都不想做，还有更简单的选择：手工设计统计特征（Hand-crafted Features）

对每条 (32,3) 序列提取如下特征：

• 时域统计：均值、标准差、峰值、峰峰值、RMS、斜率
• 频域特征：FFT 主频、能量集中度、谱熵
• 变化率：差分最大值、上升时间、过冲量
• 相关性：电流 vs 电压 相关系数、相位差估计

def extract_stats_features(x):# x: (32, 3) → current, voltage, positionmean = x.mean(axis=0)           # (3,)std = x.std(axis=0)             # (3,)peak = x.max(axis=0)            # (3,)rms = np.sqrt(np.mean(x**2, axis=0))  # (3,)diff = np.diff(x, axis=0)slew_rate = np.abs(diff).max(axis=0)  # 最大变化率return np.concatenate([mean, std, peak, rms, slew_rate])  # (15,)

• 优点：完全无需训练、可解释性强、计算极快
• 缺点：表达能力有限、无法捕捉复杂模式（如振荡频率变化）

总结流程：

原始数据 (20e6, 32, 3)↓
【方案 A（推荐）】
→ 使用轻量 CNN / Transformer + MAE 自重建预训练（无监督）
→ 提取 64D embedding
→ 流式保存到 features.h5【方案 B（简单可靠）】
→ 手工提取统计特征（均值、RMS、变化率等）→ 得到 20~50D 特征
→ 直接用于 IPCA + KMeans↓
Incremental PCA → 降维至 32D（可选）↓
MiniBatchKMeans 聚类 → 获取 cluster_id↓
Cluster 内按 novelty/stability 分层采样

如果 embedding_dim > 32，且数据量巨大 → 建议用 IPCA 再压缩一下；如果只是为了聚类，64D 可直接上 MiniBatchKMeans。

附录

HDF5 数据模型

HDF5（Hierarchical Data Format version 5） 是一种专为 大规模数值数据 存储与高效访问设计的文件格式。

HDF5 文件（本身就是一个对象）可以被视为一个 容器（或组），用于存放 各种异构数据对象（或数据集）。这些数据集可以是图像、表格、图形，甚至是文档，例如 PDF 或 Excel：

HDF5 数据模型中的两个主要对象是 组 和 数据集。HDF5 数据模型中还有多种其他对象来支持组和数据集，包括 数据类型、数据空间、属性 和 特性。

假设上述 HDF5 文件中有两个组：Viz 和 SimOut。

• Viz 组下包含各种图像以及一张与 SimOut 组共享的表格。
• SimOut 组包含一个三维数组、一个二维数组，以及一个链接到另一个 HDF5 文件中二维数组的链接。

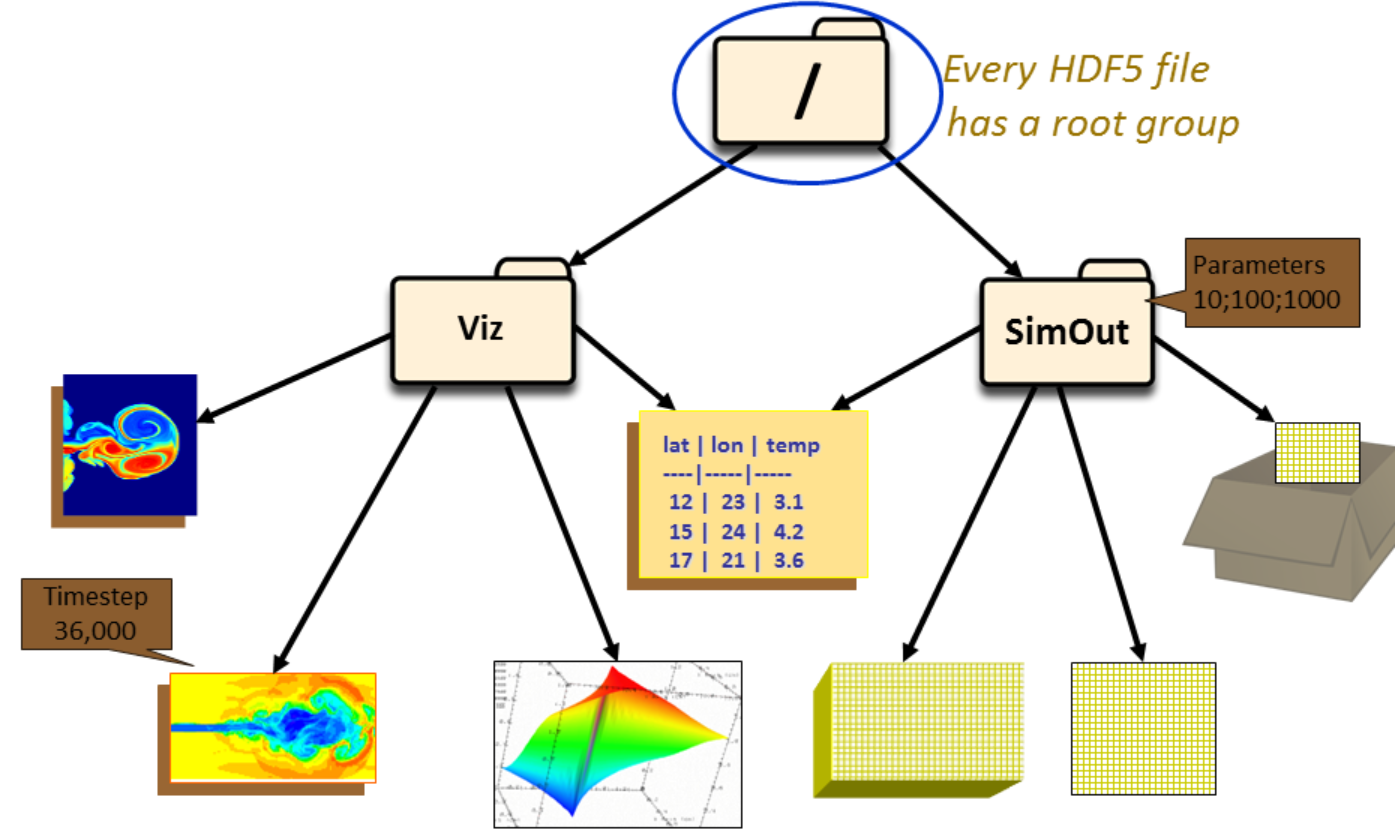
对组及其成员的操作在许多方面类似于在 UNIX 中对目录和文件的操作。与 UNIX 的目录和文件一样，HDF5 文件中的对象通常通过提供它们的完整（或绝对）路径名来描述。

• / 表示根组。
• /foo 表示根组中名为 foo 的成员。
• /foo/zoo 表示组 foo 的成员，而 foo 组本身是根组的成员。

HDF5 数据集组织并包含 raw 数据值。一个数据集除了数据本身外，还包括 描述数据的元数据：

在这张图中，数据被存储为大小为 4 × 5 × 6 的三维数据集，使用整数数据类型。它包含属性 Time 和 Pressure，且该数据集采用了块状存储并进行了压缩。

使用 Python 创建 HDF5 文件和数据集

使用 Python 来 创建 HDF5 文件，必须：

• 指定属性列表（或使用默认值）
• 创建文件
• 关闭文件（如有需要，也关闭属性列表）。

下面的 Python 示例创建了一个文件 file.h5，然后关闭它。生成的 HDF5 文件只包含一个根组：

import h5py
file = h5py.File ('file.h5', 'w')
file.close ()

使用 w 作为文件访问标志调用 h5py.File 将创建一个新的 HDF5 文件，并覆盖同名的已有文件。file 是打开文件后返回的文件句柄。文件使用完毕后必须将其关闭。当未指定属性列表时，将使用默认的属性列表。

如前所述，HDF5 数据集由原始数据以及描述数据的元数据（数据类型、空间信息和属性）组成。要 创建数据集，必须：

• 定义数据集特性（数据类型、数据空间、属性）。
• 决定将数据集附加到哪个组。
• 创建数据集。
• 关闭步骤 3 中的数据集句柄。

下面的代码摘录显示了在文件 dset.h5 中创建一个 4×6 整数数据集 dset 所需的调用。该数据集将位于根组中：

dataset = file.create_dataset("dset",(4, 6), h5py.h5t.STD_I32BE)

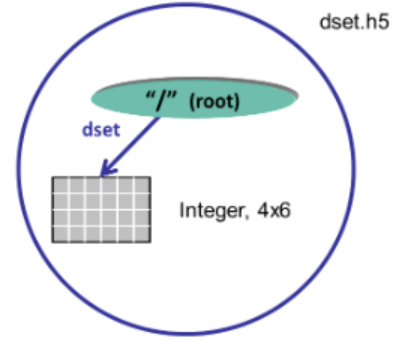
使用 Python 时，数据空间的创建作为参数包含在数据集创建方法中。只需一次调用即可创建一个 4 × 6 的整数数据集 dset。指定了预定义的 大端 32 位整数数据类型。create_dataset 方法在根组（文件对象）中创建该数据集。该数据集由 Python 接口关闭。

创建或打开数据集后，可以向其 写入数据：

data = np.zeros((4,6))
for i in range(4):for j in range(6):data[i][j]= i*6+j+1dataset[...] = data       <-- Write data to dataset
dataset[...] = data       <-- 将数据写入数据集
data_read = dataset[...]  <-- Read data from dataset
data_read = dataset[...]  <-- 从数据集读取数据

HDF5 组是一种结构，包含零个或多个 HDF5 对象。在 创建组 之前，必须获取要创建该组的位置标识符。下面是所需的步骤：

• 决定将组放置在哪里——在“根组”（或文件标识符）中，还是在其他组中。如果组尚未打开，则打开它。
• 定义属性或使用默认值。
• 创建组。
• 关闭组。

下面的代码 以读写权限打开数据集 dset.h5，并 在根组中创建一个名为 MyGroup 的组。由于未指定属性，因此使用默认值：

import h5py
file = h5py.File('dset.h5', 'r+')  
group = file.create_group ('MyGroup')
file.close()

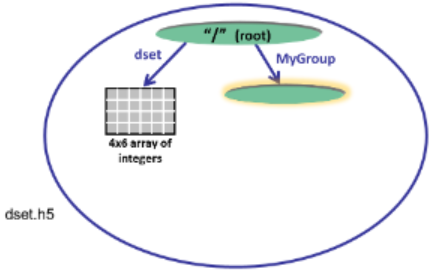
要 创建属性，必须先打开希望附加属性的对象。然后可以根据需要创建、访问并关闭该属性：

• 打开想要添加属性的对象。
• 创建属性
• 写入属性
• 关闭属性及其所附属的对象。

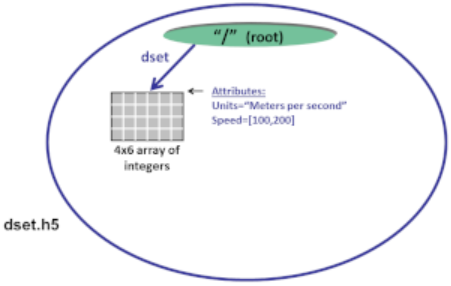
在 Python 中创建属性的调用中指定了数据空间、数据类型和数据：

dataset.attrs["Units"] = 'Meters per second'  <-- Create string
dataset.attrs["Units"] = 'Meters per second'  <-- 创建字符串
attr_data = np.zeros((2,))
attr_data[0] = 100
attr_data[1] = 200
dataset.attrs.create("Speed", attr_data, (2,), 'i') <-- Create Integer
dataset.attrs.create("Speed", attr_data, (2,), 'i') <-- 创建整数

批处理（Batch processing）

批处理的工作原理

• 数据收集：数据随时间从 各种来源 收集，并存储直至准备好进行处理；
• 批处理执行：批处理作业 依据计划（例如，每夜）或定义的数据阈值触发；
• 输出生成：批处理执行后的结果以多种形式生成，包括报告和 数据库更新。

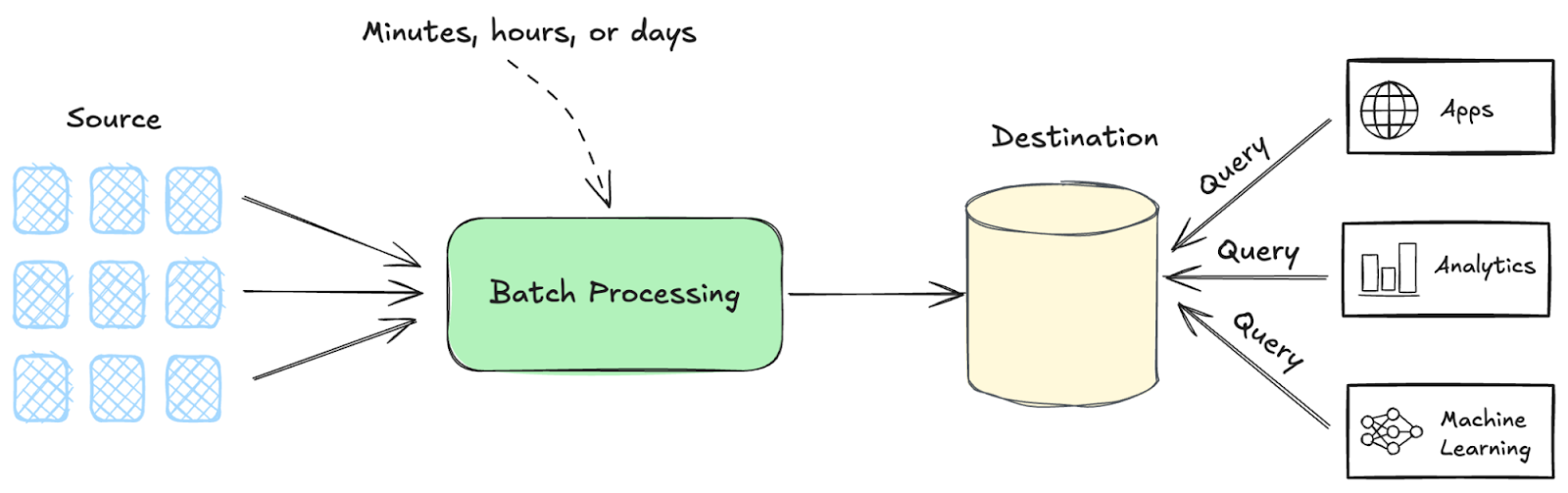
批处理 VS 流处理（Stream processing）

在批处理和流处理之间的选择体现了 时效性 与 全面性 之间的权衡。

• 批处理在预定窗口内以 大块、离散 的形式处理数据，这些块称为 批次。批处理最适用于 数据完整性 至关重要的场景，如日终报告或库存管理。
• 流式处理在 数据实时到达时进行处理，毫无延迟。流式处理在需要 即时洞察 的场景中表现出色，如欺诈检测系统或实时仪表盘。

微批处理（Micro-batch processing）是一种混合方法，结合了批处理和流处理的优势。

• 在这种方式中，数据以 小批次 在 频繁的间隔 内进行处理，从而在提供 更快洞察 的同时，仍然保持批处理所具备的 数据完整性。
• 该技术通常用于需要 实时或近实时分析 的场景，但 数据量过大，传统流处理方法无法处理。