当前位置：首页 > news >正文

MATLAB 实现基于短时傅里叶变换 (STFT) 的音频信号时频分析与可视化

news 2025/10/25 8:51:33

短时傅里叶变换 (STFT) 是分析非平稳信号的常用工具，广泛应用于音频处理、语音识别等领域。本文将通过 MATLAB 实现 STFT 的完整流程，包括音频读取、参数设置、时频分析、结果可视化，并对比不同窗函数对分析结果的影响，帮助读者理解 STFT 的原理及工程应用。

% 基于STFT的音频信号时频分析与可视化
% 功能：读取音频文件，进行短时傅里叶变换，分析并可视化时频特征，对比不同窗函数效果clear; clc; close all;%% 1. 读取音频文件（可替换为自己的音频，支持.wav格式）
% 若没有音频文件，可使用MATLAB内置示例信号
use_example_signal = true;  % 设为true使用内置信号
if use_example_signal% 生成示例信号：2秒，采样率16000Hz，包含两个频率随时间变化的正弦波fs = 16000;          % 采样率t = 0:1/fs:2;        % 时间向量f1 = 500 + 1000*t;   % 第一个信号频率（500-2500Hz线性变化）f2 = 3000 - 1000*t;  % 第二个信号频率（3000-1000Hz线性变化）x = sin(2*pi*cumsum(f1)/fs) + 0.5*sin(2*pi*cumsum(f2)/fs);  % 生成信号
else% 读取外部音频文件（需保证文件路径正确）[x, fs] = audioread('test_audio.wav');  % 替换为实际音频路径if size(x, 2) > 1x = mean(x, 2);  % 若为立体声，转为单声道endt = (0:length(x)-1)/fs;  % 时间向量
end
disp(['信号长度：', num2str(length(x)/fs), '秒，采样率：', num2str(fs), 'Hz']);%% 2. 设置STFT参数
win_len = 1024;       % 窗长（影响频率分辨率：窗越长，频率分辨率越高）
overlap = 0.75;       % 重叠率（影响时间分辨率：重叠越高，时间分辨率越高）
nfft = 2048;          % FFT点数（通常取大于等于窗长的2的整数次幂）
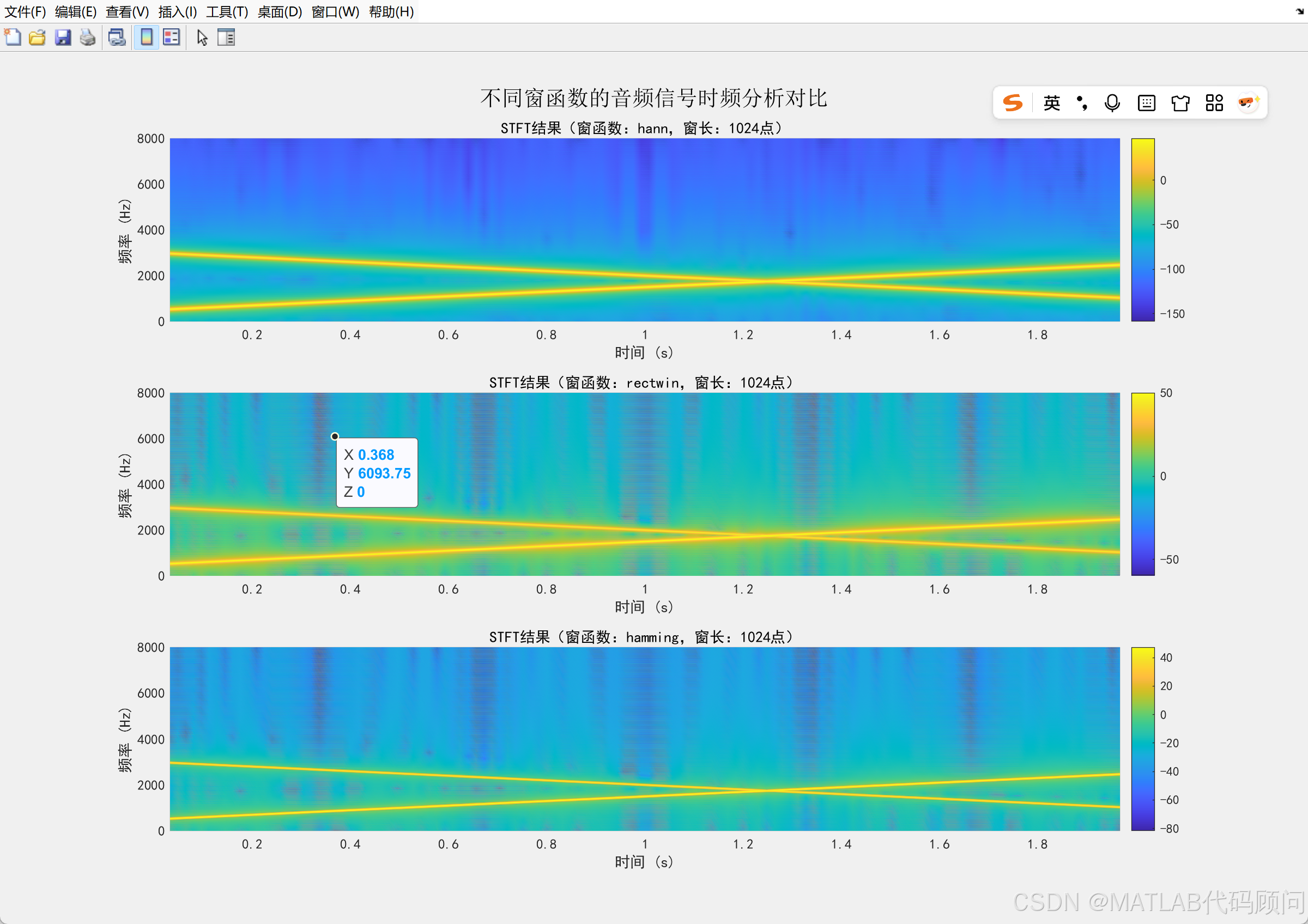
win_types = {'hann', 'rectwin', 'hamming'};  % 待对比的窗函数%% 3. 执行STFT并可视化
figure('Position', [100, 100, 1200, 800]);
for i = 1:length(win_types)win = feval(win_types{i}, win_len);  % 生成窗函数% 执行STFT[S, f, t_stft] = stft(x, fs, ...'Window', win, ...'OverlapLength', round(overlap*win_len), ...'FFTLength', nfft);power_S = abs(S).^2;  % 计算功率谱（幅度平方）% 绘制时频图subplot(length(win_types), 1, i);pcolor(t_stft, f, 10*log10(power_S));  % 转换为分贝(dB)shading interp;  % 平滑着色colorbar;xlabel('时间 (s)');ylabel('频率 (Hz)');title(['STFT结果（窗函数：', win_types{i}, '，窗长：', num2str(win_len), '点）']);ylim([0 fs/2]);  % 只显示正频率（奈奎斯特频率以内）set(gca, 'FontName', 'SimHei');  % 支持中文显示
end
sgtitle('不同窗函数的音频信号时频分析对比');%% 4. 绘制原始信号波形
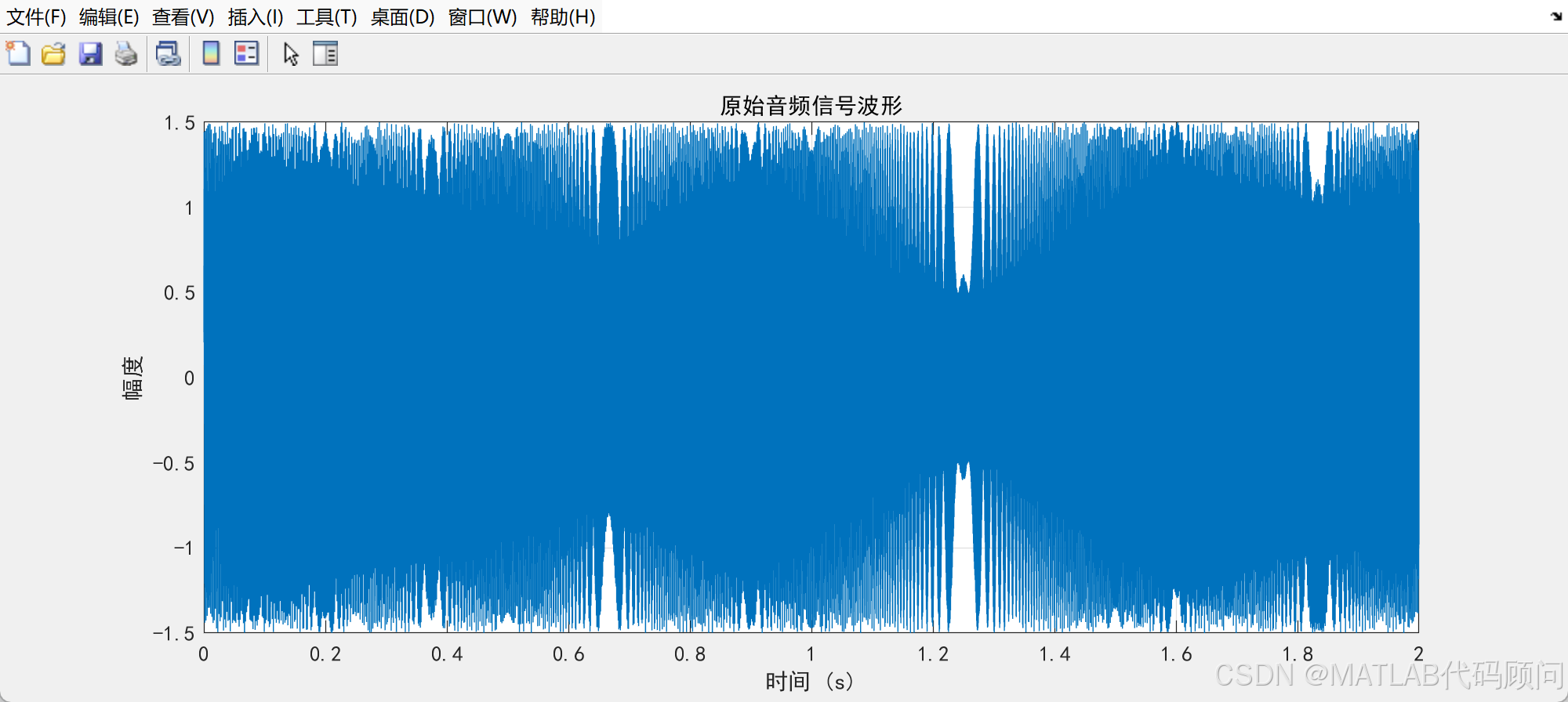
figure('Position', [100, 300, 1000, 400]);
plot(t, x);
xlabel('时间 (s)');
ylabel('幅度');
title('原始音频信号波形');
xlim([0 max(t)]);
grid on;
set(gca, 'FontName', 'SimHei');

程序结果