当前位置：首页 > news >正文

【MATLAB例程】自适应渐消卡尔曼滤波，背景为二维雷达目标跟踪，基于扩展卡尔曼（EKF）|附完整代码的下载链接

news 2025/10/25 8:48:00

在这里插入图片描述

通过引入渐消因子 $\lambda_k$ 对预测协方差进行放大修正，使滤波器能够在机动阶段快速响应状态变化、在平稳阶段保持估计稳定性。结合EKF，使用二维雷达观测进行目标跟踪、位置滤波

文章目录

程序概述
运行结果
MATLAB源代码
- 运行指南

程序概述

程序给出了MATLAB的基于**自适应渐消扩展卡尔曼滤波(Adaptive Fading Extended Kalman Filter, AFEKF)**的二维雷达目标跟踪算法，并与标准扩展卡尔曼滤波(EKF)进行性能对比。程序模拟了包含多种机动模式的目标运动场景，验证了自适应渐消滤波在模型失配情况下的鲁棒性优势。

目标运动模型：

状态向量: [x, vx, y, vy]' - 包含二维位置和速度
运动场景:
- 匀速直线运动
- 加速机动

雷达观测模型

观测量: 极坐标系下的距离和方位角 [r, θ]'
测量噪声:
- 距离标准差: σᵣ = 2米
- 角度标准差: σθ = 0.2° (0.0035弧度)
非线性处理: 使用雅可比矩阵线性化观测方程
自适应渐消机制：

lambda = max(λ_min, min(λ_max, trace(V) / trace(S)))
P_pred = lambda × P_pred

渐消因子范围: 1.0 ≤ λ ≤ 2.0
自适应准则: 基于实际新息协方差与理论值的比值
作用效果: 当检测到模型失配时自动放大预测协方差，增强对新观测的响应

算法流程：

预测步骤:
- 状态预测: x̂(k|k-1) = F·x̂(k-1|k-1)
- 协方差预测: P(k|k-1) = F·P(k-1|k-1)·F’ + Q
更新步骤:
- 计算雅可比矩阵H
- 卡尔曼增益: K = P·H’·(H·P·H’+R)⁻¹
- 状态更新: x̂(k|k) = x̂(k|k-1) + K·(z - h(x̂))

在预测步骤后增加渐消因子调整:
```
P(k|k-1) ← λ(k) × P(k|k-1)
```
λ(k)根据新息序列实时计算，自动适应系统动态变化

运行结果

轨迹对比：
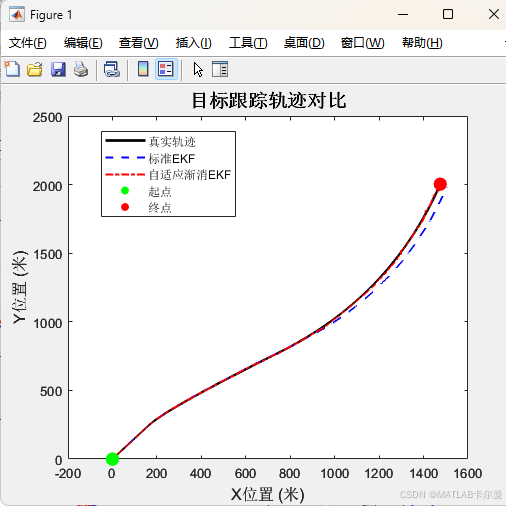
在这里插入图片描述
位置误差曲线：

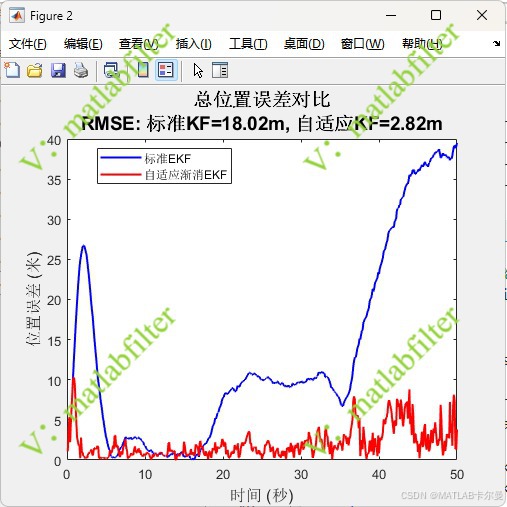
位移与速度曲线、误差曲线：

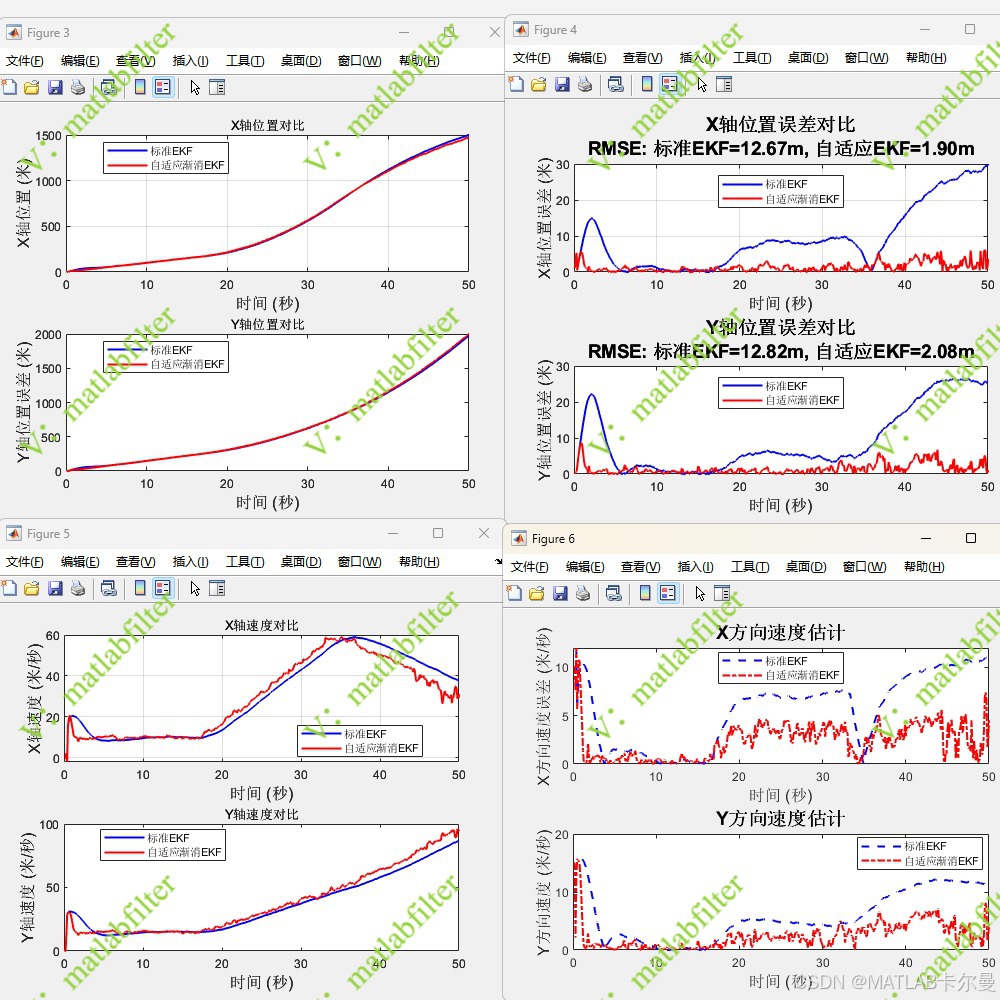
命令行输出：

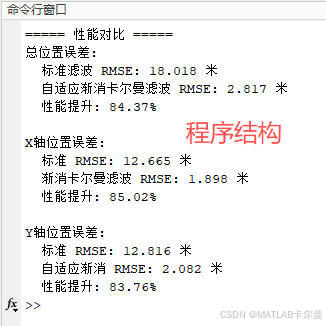
MATLAB源代码

部分代码如下：

% 自适应渐消卡尔曼滤波-EKF - 二维雷达目标跟踪
% 状态向量: [x, vx, y, vy]' (位置和速度)
% 2025-10-15/Ver1
% 作者: matlabfilter
clear; close all; clc;
rng(0);%% 仿真参数设置
dt = 0.1;           % 采样时间(秒)
T = 50;             % 仿真总时间(秒)
N = T/dt;           % 采样点数% 真实目标运动轨迹(含机动)
true_x = zeros(4, N);
true_x(:,1) = [0; 10; 0; 15];  % 初始状态 [x, vx, y, vy]% 生成真实轨迹(包含机动)
for k = 2:Nif k < N/3% 匀速运动ax = 0; ay = 0;elseif k < 2*N/3% 加速机动ax = 3; ay = 2;else% 加速机动2ax = -2; ay = 3;endtrue_x(1,k) = true_x(1,k-1) + true_x(2,k-1)*dt + 0.5*ax*dt^2;true_x(2,k) = true_x(2,k-1) + ax*dt;true_x(3,k) = true_x(3,k-1) + true_x(4,k-1)*dt + 0.5*ay*dt^2;true_x(4,k) = true_x(4,k-1) + ay*dt;
end