当前位置：首页 > news >正文

GJOI 10.20/10.22 题解

news 2025/10/25 7:41:53

1.CF1852A Ntarsis’ Set

题意

在这里插入图片描述
多组测试数据 $1\le T\le 10$ ， $1\le n\le 10^5$ ， $1\le k\le 10^9$ ，保证 $a_i$ 单调递增， $a_i\in[1,10^9]$ 。

思路

赛时写了一个很奇妙的做法。首先若 $a_1\neq 1$ ，答案必然是 $1$ 。于是只讨论 $a_1=1$ 的情况。

即每次都是先删除 $S$ 最小的数，题意转化为 $k + 1$ 天要删的第 $1$ 个数。考虑研究每天删去的第一个数有什么性质。那就拿一个样例：

5 6
1 2 6 8 11
每次删去：1  2  6  8 113  4 10 13 165  7 15 18 219 12 20 23 26
14 17 25 28 31
19 22 30 33 36
24(ans)

我们发现，删到一定程度，相邻天数总是相差 $n = 5$ 。这是为何？

首先第 $11$ 大总是跑在前面且差 $5$ ，因为实时的第 $11$ 小，前面已经删掉了 $5$ 个数（包括自己，下同），所以第 $11$ 大会一直往后推 $5$ 。
对于第 $8$ 小：
- 前面删去 $4$ 个数，按说是 $8 + 4 = 12$ ，但是前面又删一个 $11$ ，于是还要 $12 + 1 = 13$ 。
- $13$ 后面亦然重复这个 $+ 4 + 1 = + 5$ 的过程。
对于第 $6$ 小：
- 前面删去 $3$ 个数，于是 $6 + 3 = 9$ ，前面又有 $8$ 删去，于是 $9 + 1 = 10$ ；
- 第三天前面又删 $3$ 个数， $10 + 3 = 13$ ，一是前面有个 $11$ 已经删掉，二是 $13$ 在第二天的第 $8$ 大被删去。于是 $13 + 1 + 1 = 15$ 。
- 后面亦然重复这个 $+ 3 + 1 + 1 = + 5$ 的过程。
以此类推，推导第 $1$ 小：
- $1$ 前面 $1$ 个数被删了， $1 + 1 = 2$ 有占位， $2 + 1 = 3$ 结束第二天；
- 前面又被删掉 $1$ 个数， $3 + 1 = 4$ 但是 $4$ 被删过于是 $4 + 1 = 5$ ；
- $5 + 1 = 6$ 但是 $6$ 被删过了，后面 $7, 8$ 都被删过了，于是 $6\to 9$ ；
- 后面 $10\sim 13$ 都被删过了于是 $9\to 14$ ，亦然重复这个 $+ 1 + 1 + 1 + 1 + 1 = 5$ 的过程。

考虑这个“删过”的本质？就是 $a_{2\sim n}$ 先一步到达了某些数，导致“删过”；而 $a_1=1$ 的增速最慢，于是前面总是 $n$ 个数被删了（后面的数也会 $+ 5$ ，于是形成某种周期），下一次就要删 $+ 5$ 之后的数了。

考虑加速这个过程。设删过 $p os$ 个数，一开始 $c u r = 1$ ，若 $cur+pos\ge a_{pos+1}$ ，说明跑到一个被删过的数，于是 $pos\leftarrow pos+1$ ，直到 $cur+pos<a_{pos+1}$ 。前面删过多少数是可以继承的。直到 $p os = n$ 时，前面就总是删过 $n$ 个数了。记录这样的 $+ p os$ 进行了 $t i c k$ 轮，若 $t i c k < k$ 就可以直接 break 输出答案；否则答案再加 $(k-tick)\times n$ 。

时间复杂度 $\le O(n)$ 。CF 218ms。

他们都夸我注意力惊人怎么办？还是推荐一篇严谨一点的 $O (n)$ 做法。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=1e5+9,inf=1e18;
ll id,Q,n,k;
ll a[N];
int main()
{freopen("superset.in","r",stdin);freopen("superset.out","w",stdout);scanf("%lld%lld",&id,&Q);while(Q--){scanf("%lld%lld",&n,&k);for(int i=1;i<=n;i++)scanf("%lld",&a[i]);if(a[1]!=1){puts("1");continue;}//a[1]=1ll cur=1,pos=1,tick=0;a[n+1]=inf;while(1){while(pos<=n){if(a[pos]<cur+pos&&cur+pos<a[pos+1])break;pos++;}cur+=pos;tick++;if(tick==k)break;if(pos==n)break;}if(tick==k){printf("%lld\n",cur);continue;}cur+=(k-tick)*n;printf("%lld\n",cur);}return 0;
}

2.CF1936C Pokémon Arena

题意

在这里插入图片描述
多组测试数据 $1\le T\le 5$ ， $1\le n\times m\le 2\times 10^5$ 。

思路

赛时觉得还算可做，但是没有往建模去想。于是去后面拼暴力了。

首先对于三只宝可梦 $x, y, z$ 的同一个属性 $j$ ，有 $a_{x,j}>a_{y,j}>a_{z,j}$ 并且 $x$ 在擂台。雇佣依次雇佣三只宝可梦并充能，费用是 $a_{x,j}-a_{y,j}+c_y)+(a_{y,j}-a_{z,j}+c_z)=a_{x,j}-a_{z,j}+c_y+c_z$ 。但显然直接雇佣宝可梦 $z$ 给它充能，只用 $a_{x,j}-a_{z,j}+c_z$ 。

发现要打败 $x$ 的某个性质，只雇佣一只来搞是更优的。

到这里发现宝可梦和性质特别多，于是可以考虑建模。剩下的交给 dijkstra 就好了。

对于任意一对点 $(x, y)$ ，首先 $x$ 连向 $m$ 个性质点 $x_{1\sim m}$ 然后 $x_{j}$ 和 $y_{j}$ 之间双向边，边权分别是给 $x, y$ 的 $j$ 性质充能所用的价值，即 $x_j\to y_j:\max(a_{y,j}-a_{x,j},0),y_j\to x_j:\max(a_{x,j}-a_{y,j},0)$ 。

但是挂着个雇佣费怎么整？我们直接令 $x$ 的性质点出去 $x_{out}$ 花费 $c_x$ 即可。

但是建图规模来到 $n^2m$ 。我们发现有个 $max(a_{y,j}-a_{x,j},0)$ 。有的边必然边权为 $0$ 。于是 $n$ 个点的 $j$ 属性排序，连成一条链，这相当于把一些边权为 $0$ 的边略去。于是 $x_j$ 充能到 $y_j$ 的费用就直接在链上走过去即可（这里巧妙利用了绝对值的性质）。

然后跑 $1\to n$ 最短路即可。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pll pair<ll,ll>
#define fi first
#define se second
#define mk make_pair
const ll N=4e5+9,M=6e5+9,inf=1e18;
ll id,Q,n,m;
ll c[N];
vector<ll>a[N];
struct edge
{ll to,next,w;
}e[M<<1];
ll idx,head[M];
void addedge(ll u,ll v,ll w)
{idx++;e[idx].to=v;e[idx].next=head[u];e[idx].w=w;head[u]=idx;
}
ll dis[M];
bool vis[M];
pll b[N];
void dijkstra(ll s)
{for(int i=0;i<=n+n*m;i++){dis[i]=inf;vis[i]=0;}priority_queue<pll>q;dis[s]=0;q.push(mk(0,s));while(!q.empty()){pll tem=q.top();q.pop();ll u=tem.se;if(vis[u])continue;vis[u]=1;for(int i=head[u];i;i=e[i].next){ll v=e[i].to,w=e[i].w;if(dis[u]+w<dis[v]){dis[v]=dis[u]+w;q.push(mk(-dis[v],v));}}}
}
int main()
{freopen("pokemon.in","r",stdin);freopen("pokemon.out","w",stdout);scanf("%lld%lld",&id,&Q);while(Q--){idx=0;memset(head,0,sizeof(head));memset(e,0,sizeof(e));scanf("%lld%lld",&n,&m);for(int i=1;i<=n;i++){scanf("%lld",&c[i]);for(int j=1;j<=m;j++){addedge(i,i+j*n,0);addedge(i+j*n,i,c[i]);}}for(int i=1;i<=n;i++){a[i].resize(m+1);for(int j=1;j<=m;j++)scanf("%lld",&a[i][j]);}for(int j=1;j<=m;j++){for(int i=1;i<=n;i++)b[i]=mk(a[i][j],i);sort(b+1,b+n+1);for(int i=1;i<n;i++){addedge(b[i].se+j*n,b[i+1].se+j*n,0);addedge(b[i+1].se+j*n,b[i].se+j*n,b[i+1].fi-b[i].fi);}}dijkstra(1);printf("%lld\n",dis[n]);}return 0;
}

反思

没有敢于去建模啊，不过这题建模还是太厉害了，感觉是图论建模的 trick 见少了。同时也没有在赛时分析一些可行的性质……

3.CF983E NN country

nflsoi 也考过一次，这次测试的 $D .$ 题。

待补。

4.AT_code_festival_2017_qualc_f Three Gluttons

接下来是 GJOI 10.22，来到 wyx 出题 round。

1.洛谷 P9464 EGOI2023 Padel Prize Pursuit / 追梦笼式网球

题意

题目传送门添加链接描述。建议前往原题阅读题干、样例以及其解释。

思路

注意奖牌持有天数可以叠加。

考虑模拟第 $i$ 天的胜者拿到奖牌 $i$ ，奖牌 $i$ 在各个选手之间是怎么游走了。

第 $i$ 天胜者 $x_i$ ，在第 $i$ 天之后的第 $j$ 天，是 $x_i=y_j$ 赢之后第一次输，奖牌全部给了 $y_i$ 。

于是考虑开 $2 m$ 个点，每天 $x_i\leftarrow y_i$ 连边， $x_i\to y_j$ 连边， $y_j$ 的含义如上所述。如果 $x_i$ 赢了后面没有输过，就单独开一个虚拟节点 $e n d$ ， $x_i\to end$ 。

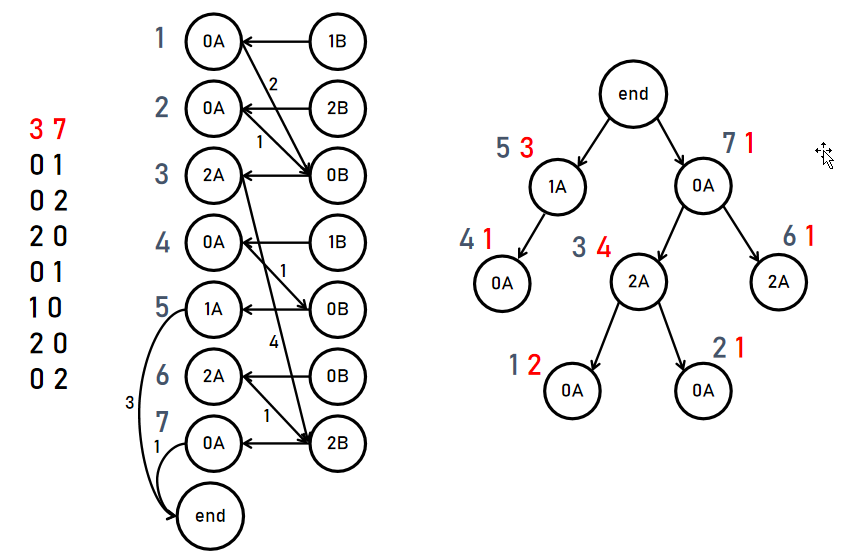
在这里插入图片描述
对于第 $2$ 个样例如此建图。而若把胜点和败点合并，就会变成一棵 $m + 1$ 个节点的树，并且将边权转化为点权。

这个树保证了节点对应的胜点，浅处胜利时间大于深处胜利时间，即将把天数 $i$ 作为节点编号，在天数 $i$ 拿到奖牌 $i$ ，奖牌 $i$ 在各个人之间的游走，就是从 $i\to end$ 途径过的人，每个人持有的时间就是途径的人各自的点权和。在这里插入代码片

于是从 $e n d$ 开始 dfs，维护 $e n d$ 到 $i$ 路径上，维护每个人的点权和，就是 $i$ 奖牌被每个人拿的天数。

考虑维护持有天数最多的人 $ma$ ，加入奖牌 $i$ 和最开始拿着 $i$ 的 $u$ ，不难发现更新之后的 $m a^{'}$ 要么是 $i$ 要么是 $ma$ 。根据各自点权和以及编号大小更新即可。

时间复杂度 $O (n)$ 。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=2e5+9;
ll n,m;
struct term
{ll x,y;
}p[N];
map<ll,ll>pos,pre;
ll ANS[N],val[N];
vector<ll>G[N],Cnt;
void dfs(ll u,ll ma)
{for(auto v:G[u]){ll id=pos[v];Cnt[id]+=val[v];if(Cnt[id]>Cnt[ma]){ANS[id]++;dfs(v,id);}else if(Cnt[id]==Cnt[ma]){ll z=min(ma,id);ANS[z]++;dfs(v,z);}else {ANS[ma]++;dfs(v,ma);}Cnt[id]-=val[v];}
}
int main()
{freopen("ybt.in","r",stdin);freopen("ybt.out","w",stdout);scanf("%lld%lld",&n,&m);for(int i=1;i<=m;i++){ll x,y;scanf("%lld%lld",&x,&y);p[i]=(term){x+1,y+1};}ll en=m+1;for(int i=m;i>=1;i--)//倒插更方便查询i天赢得人在哪一天第一次输{if(!pre[p[i].x]){G[en].push_back(i);val[i]=m+1-i;}else{ll z=pre[p[i].x];G[z].push_back(i);val[i]=z-i;}pos[i]=p[i].x;pre[p[i].y]=i;}Cnt.resize(n+3);dfs(en,n+1);for(int i=1;i<=n;i++)printf("%lld ",ANS[i]);return 0;
}

2.CF1310D Tourism

题意

在这里插入图片描述
$n\le 80,k\le 10$ 。

思路

长度为 $k + 1$ 的游走序列 $p$ ，其中 $p_1=p_{k+1}=1$ 。

一开始想要 $2\sim k$ 全部枚举，然后判断不合法的情况，计算上一次出现的下标 $pre_x$ ，当前下标 $i$ 能选 $x$ 当且仅当 $i-pre_x$ 为偶数——这个必然跑满。

但是这个是可以优化的。我们直接考虑合法情况，以及折半搜索。

我们直接枚举 $p_3,p_5,...,p_{k-1}$ （ $k$ 是偶数，这里枚举奇数位），这里可以随便枚举。然后考虑填充偶数位，要求偶数位的数不能在奇数位出现。

我们可以类似 Floyd 的思路，预处理点 $x, z$ 之间， $dis_{x,y}+dis_{y,z}$ 最小的最佳途经点 $y$ ，要求 $y\neq x,y\neq z$ 。为了防止 $p_1,p_3,p_5,...,p_{k-1}$ 都是不同的极端占用情况，至少要预处理出两个点之间 $5$ 组优解。

时间复杂度 $O(n^{\frac{k}{2}-1})$ 。

代码

#pragma GCC optimise(2)
#pragma GCC optimise(3,"Ofast","inline")
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=82,inf=1e18,mod=1e9+7;
ll n,k;
ll G[N][N];
ll pass[N][N][7];
ll a[N],vis[N];
ll ans=inf;
ll dis(ll i,ll j,ll k)
{if(k==0)return inf;return G[i][k]+G[k][j];
}
void dfs(ll id)//决定奇数位4个 
{if(id>k/2){ll ret=0;for(int i=1;i<=k/2;i++){ll nxt=i+1;if(nxt>k/2)nxt=1;for(int t=0;t<=5;t++){if(!vis[pass[a[i]][a[nxt]][t]]){ret+=dis(a[i],a[nxt],pass[a[i]][a[nxt]][t]);break;}}}ans=min(ans,ret);return;}for(int i=1;i<=n;i++){a[id]=i;vis[i]++;dfs(id+1);a[id]=-1;vis[i]--;}
}
int main()
{
//	freopen("luogu.in","r",stdin);
//	freopen("luogu.out","w",stdout);scanf("%lld%lld",&n,&k);for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)scanf("%lld",&G[i][j]);for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){for(int k=1;k<=n;k++){if(k==i||k==j)continue;pass[i][j][6]=k;for(int t=5;t>=0;t--)//前6优的途经点pass (0~5){if(dis(i,j,pass[i][j][t+1])<dis(i,j,pass[i][j][t]))swap(pass[i][j][t+1],pass[i][j][t]);else break;}}}}a[1]=1;vis[1]=1;dfs(2);printf("%lld",ans);return 0;
}