算法leetcode｜96. 不同的二叉搜索树（多语言实现）

---

---

96. 不同的二叉搜索树：

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

样例 1：

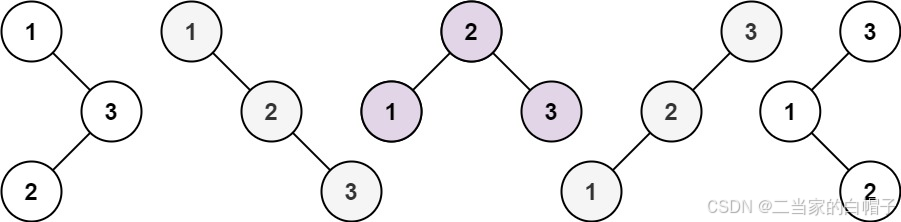
输入：n = 3输出：5

样例 2：

输入：n = 1输出：1

提示：

• 1 <= n <= 19

---

分析：

• 面对这道算法题目，二当家的再次陷入了沉思。
• 要穷举所有可能不同的二叉搜索树，每个节点需要遍历 1 到 n 。
• 由于每棵树的左右子树同样也是树，使用递归套娃大法就非常直观，将问题不断分解成子问题，比循环简单。
• 二叉搜索树本身有着一些限制，左子树所有的节点不大于自己，右子树所有的节点不小于自己，所以当确定父节点的值之后，子树的取值范围也可以确定，并且取值范围会缩小，这就有了递归回归的条件。
• 将每个节点都在范围内遍历，每次遍历都去生成所有可能的左右子树，再将所有可能的左子树和可能的右子树分别组合就是结果。
• 但是这是将所有二叉搜索树本身穷举出来，而题目只是要求返回数量即可，会不会有更简单的方式？
• 想想二叉搜索树的定义，由于所有节点都是不同的，所以就和具体值无关，只和节点数量有关，那么就可以转化为一个数学问题，从1个节点开始计算，此时只会有一种树（参看百科 卡特兰数 ）。

---

题解：

rust：

impl Solution {pub fn num_trees(n: i32) -> i32 {// 提示：我们在这里需要用 i64 类型防止计算过程中的溢出let mut c = 1i64;(0..n as i64).for_each(|i| {c = c * 2 * (2 * i + 1) / (i + 2);});return c as i32;}
}

---

go：

func numTrees(n int) int {c := 1for i := 0; i < n; i++ {c = c * 2 * (2*i + 1) / (i + 2)}return c
}

---

c++：

class Solution {
public:int numTrees(int n) {long long c = 1;for (int i = 0; i < n; ++i) {c = c * 2 * (2 * i + 1) / (i + 2);}return (int) c;}
};

---

python：

class Solution:def numTrees(self, n: int) -> int:c = 1for i in range(0, n):c = c * 2 * (2 * i + 1) / (i + 2)return int(c)

---

java：

class Solution {public int numTrees(int n) {// 提示：我们在这里需要用 long 类型防止计算过程中的溢出long c = 1;for (int i = 0; i < n; ++i) {c = c * 2 * (2 * i + 1) / (i + 2);}return (int) c;}
}

---

非常感谢你阅读本文~
欢迎【点赞】【收藏】【评论】三连走一波~
放弃不难，但坚持一定很酷~
希望我们大家都能每天进步一点点~
本文由 二当家的白帽子：https://le-yi.blog.csdn.net/ 博客原创~

---