当前位置：首页 > news >正文

【经典算法，限时免费】LeetCode698、划分K个相等的子集（回溯解法）

news 2025/10/23 12:04:13

题目练习网址：LeetCode698、划分K个相等的子集（回溯解法）

一、题目描述

给定一个整数数组 nums 和一个正整数 k，找出是否有可能把这个数组分成 k 个非空子集，其总和都相等。

示例 1：

输入： nums = [4, 3, 2, 3, 5, 2, 1], k = 4 输出： True 说明： 有可能将其分成 4 个子集（5），（1,4），（2,3），（2,3）等于总和。

示例 2:

输入: nums = [1,2,3,4], k = 3 输出: False

提示：

1 <= k <= len(nums) <= 16
0 < nums[i] < 10000
每个元素的频率在 [1,4] 范围内

二、题目解析

这个问题有多种解法：回溯、DFS记忆化搜索、动态规划。

本篇题解主要介绍回溯解法。

往k个桶里分配n个数字

这个问题本身有点抽象，我们可以把它换成一个更加具象化的场景。

假设我们现在有k个桶和n个数字，现在我们希望把这n个数字分配在这k个桶里，使得这k个桶里各自的数字的和相等。

这很明显是一个分组问题。

其次，我们观察数据量，1 <= k <= len(nums) <= 16，并不是一个很大的数量级。

所以容易想到回溯穷举的做法。

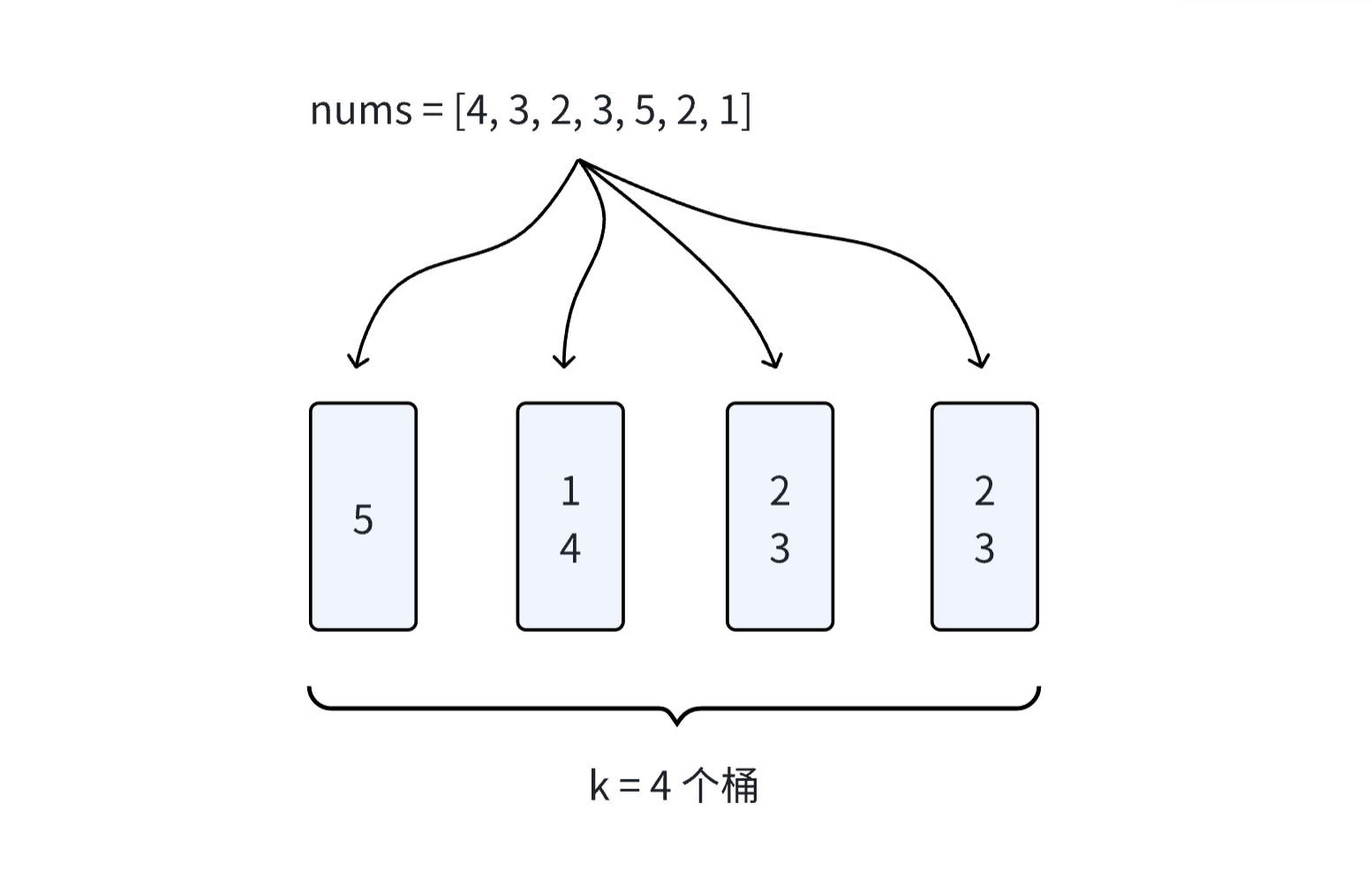
在这里插入图片描述

特殊情况的排除

显然，要完成这个问题，这n个数字构成的数字nums必须满足以下条件

这些数字的和total = sum(nums)必须能够整除k，否则一定无法使得这k个桶各自的和相等
当total能够整除k时，最后每个桶各自的和per = total // k也是非常容易算出来的
这些数字中的最大值max(nums)必须不能大于per

以示例一为例，容易计算total = 20，per = 5。

所以本题可以进行一些特殊情况的排除

class Solution:passdef canPartitionKSubsets(self, nums: List[int], k: int) -> bool:# 计算所有数字nums的和totaltotal = sum(nums)# 如果total不能整除k，直接返回Falseif total % k != 0:return False# 当total可以整除k时，计算各个桶最终到达的和perper = total // k# 如果nums中的最大值已经大于per# 那么也一定无法完成分配if max(nums) > per:return Falsepass

贪心地从大到小考虑nums数组

回溯无非是穷举，我们需要思考当人来做这个问题的时候，是如何进行穷举的。

我们会贪心地先把大的数字挑出来，把这些更大的数字先分配到桶里。

这个贪心的原理很容易理解：大的数占整个桶的空间更多，相对而言比较“笨重”，一旦确定放在某个桶里，较少的概率会发生调整。而小的数可以更加灵活地去填补每个桶剩余的缝隙，更加方便在后面进行不同桶之间的调整。

以示例一为例，nums = [4, 3, 2, 3, 5, 2, 1]，k = 4，total = 20，per = 5。

如果我们选择了数字4放在一个桶里，这个桶剩下的空间是1，我们就知道在后面只需要再找一个数字1来放到这个桶里即可。

但如果我们先选择了数字1放在一个桶里，这个桶剩下的空间是4，那么将出现较多种可能的组合，比如1+1+2，2+2，1+3，4等等，就增加了枚举的情况。

所以，基于上述的贪心思想，我们可以在回溯之前，将数字nums进行逆序排序，使得大的数字放在nums的前面而先被考虑。

nums.sort(reverse = True)

状态树的构建

既然考虑使用回溯来完成这个问题，那么自然还需要思考整个计算过程的状态树如何构建。

我们可以使用一个变量i来表示nums数组里面的元素索引。

由于nums数组本身已经进行逆序排序，所以越靠后的索引i对应的值更小。

对于每一个nums中的数字nums[i]，我们都考虑它可能会被放到某一个桶中。

考虑其中的某个状态以及其下一层的状态。

假设我们已经将nums[0] = 5和nums[1] = 4分别填入第0和第1个桶里，接下来我们要将nums[2] = 3分别尝试填入每一个桶中。

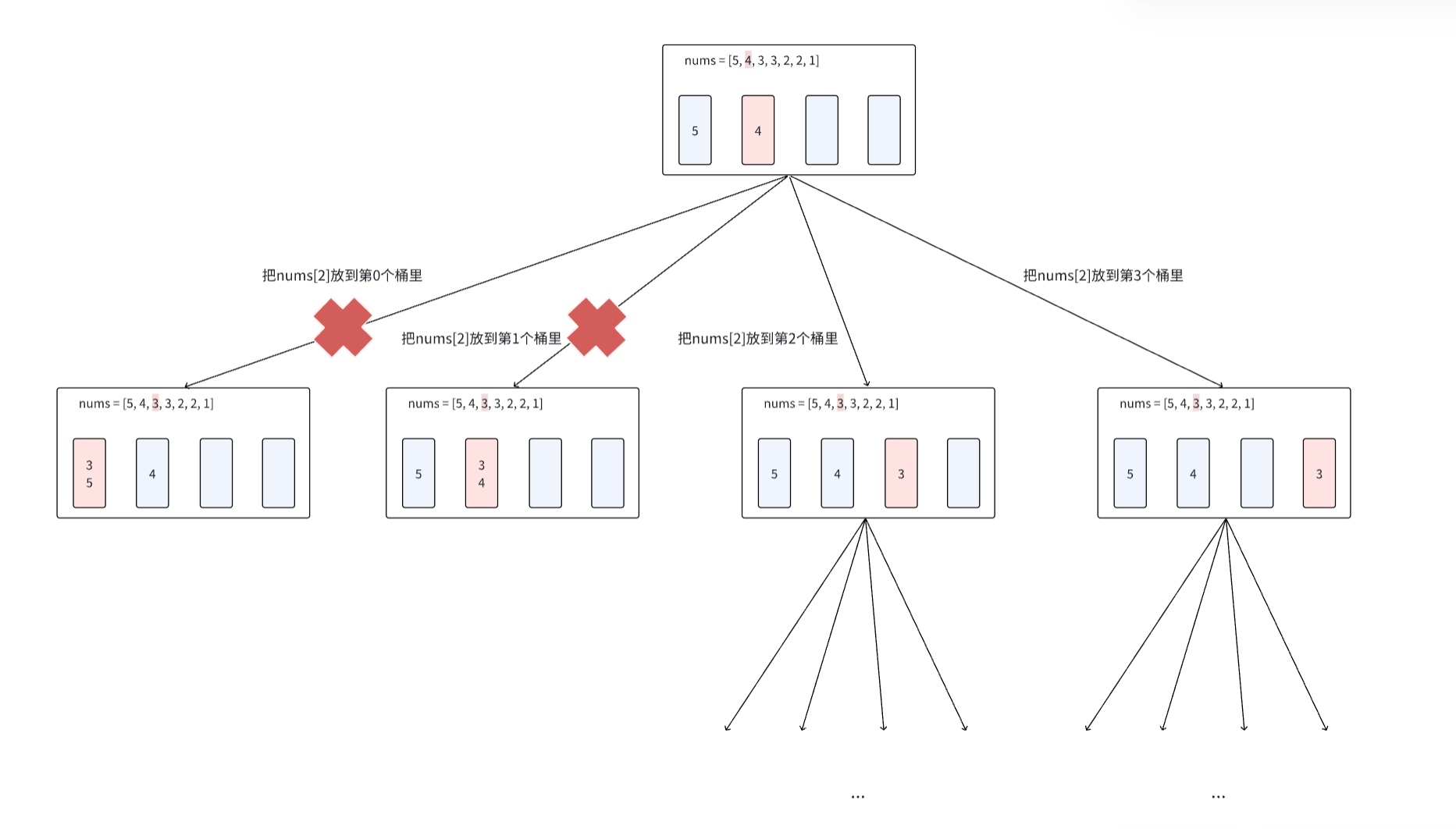
在这里插入图片描述

考虑回溯过程中的两个核心方向：纵向和横向。

纵向遍历涉及数组索引的遍历，也就是越往下层，索引i的值会增加
横向遍历涉及桶的索引的遍历，如果把桶的索引设置为j，那么从左到右的横向遍历j会增大

注意横向遍历的过程中，在进行完group[j]的状态更新之后，只有当group[j]的值不超过per，才可以继续进行递归函数的调用。

（考虑上述回溯状态树中的前两个分枝是直接不进入递归的，这也是某种意义上的剪枝）

那么我们就可以构造出如下的dfs函数来完成基本的回溯过程，仍然遵循常规的回溯模板

class Solution:def dfs(self, group, i, nums, per, n, k):# 递归终止条件：当数组索引i到达n的时候# 说明整个回溯完成，退出函数if i == n:return# 横向遍历：考虑k个不同的桶# 设置桶的索引为j，横向遍历每一个桶for j in range(k):# 状态更新：将nums[i]放入第j个桶中，# 也就是将nums[i]加到group[j]中group[j] += nums[i]# 纵向遍历，考虑下一个数字，也就是将i+1传入dfs函数中并调用# 并且group[j]的值不能超过per，否则回溯将没有意义if group[j] <= per:self.dfs(group, i+1, nums, per, n, k)# 状态回滚：将nums[i]从第j个桶中拿出# 也就是group[j]减去nums[i]group[j] -= nums[i]def canPartitionKSubsets(self, nums: List[int], k: int) -> bool:passn = len(nums)# 初始化长度为k的group数组，表示k个桶的求和情况group = [0] * k# 递归入口：传入i=0，表示nums[0]开始填入桶中self.dfs(group, 0, nums, per, n, k)pass

除此之外，我们还需要考虑函数的返回值。

题目要求当我们能够找到正确分配时返回True，所以我们可以设置一个布尔类型成员变量self.ans（如果是ACM模式则设置一个全局变量）来表示是否找到了这样的分配。

容易更新上述代码为

class Solution:def dfs(self, group, i, nums, per, n, k):# 递归终止条件：当数组索引i到达n的时候# 说明整个回溯完成，将self.ans设置为True之后，退出函数if i == n:self.ans = Truereturn# 横向遍历：考虑k个不同的桶# 设置桶的索引为j，横向遍历每一个桶for j in range(k):# 状态更新：将nums[i]放入第j个桶中，# 也就是将nums[i]加到group[j]中group[j] += nums[i]# 纵向遍历，考虑下一个数字，也就是将i+1传入dfs函数中并调用# 并且group[j]的值不能超过per，否则回溯将没有意义if group[j] <= per:self.dfs(group, i+1, nums, per, n, k)# 状态回滚：将nums[i]从第j个桶中拿出# 也就是group[j]减去nums[i]group[j] -= nums[i]def canPartitionKSubsets(self, nums: List[int], k: int) -> bool:# 计算所有数字nums的和totaltotal = sum(nums)# 如果total不能整除k，直接返回Falseif total % k != 0:return False# 当total可以整除k时，计算各个桶最终到达的和perper = total // k# 贪心地对nums进行逆序排序，减少遍历次数nums.sort(reverse = True)# 如果nums中的最大值已经大于per# 那么也一定无法完成分配if nums[0] > per:return Falsen = len(nums)# 初始化成员变量self.ans为Falseself.ans = False# 初始化长度为k的group数组，表示k个桶的求和情况group = [0] * k# 递归入口：传入i=0，表示nums[0]开始填入桶中self.dfs(group, 0, nums, per, n, k)# 返回self.ans的值来表示是否找到了答案return self.ans

需要注意的是，本题的横向遍历过程和以往的常规回溯题目（如子集问题、组合问题等等）做法稍有不同，甚至可能会有点反直觉。

在过往的题目中，横向遍历通常涉及到整个nums数组的遍历。

但本题的横向遍历则涉及了k个桶的遍历，nums数组中数字的选择，则放在了纵向上。

这是因为本题的状态树分岔较多，只有这样进行遍历才能够尽可能地剪枝降低时间复杂度。

剪枝优化减少状态树分岔

上述代码就已经能够通过一些简单用例了，但是提交时仍然因为超时无法通过全部用例。

所以很显然我们需要考虑回溯的剪枝，来排除一些重复状态和遍历。

当我们已经找到一组正确的的分配时，就无需再做回溯过程了，可以直接返回，退出函数。所以可以修改dfs递归函数的退出条件为

class Solution:def dfs(self, group, i, nums, per, n, k):# 递归终止条件：当数组索引i到达n的时候，或者已经找到一组正确的的分配时# 说明整个回溯完成，将self.ans设置为True之后，退出函数if i == n or self.ans:self.ans = Truereturnpasspass

在横向遍历的过程中，由于所有的桶都是全同的没有差别的，在更新group[j]之前，如果发现当前桶的和group[j]和上一个桶的和group[j-1]相等，那么更新group[j]将没有意义，因为更新它和之前已经考虑过的group[j-1]是一样的。

（考虑上述回溯状态树中的最后一个分岔实际上和倒数第二个分岔的分配情况是一样的）

class Solution:def dfs(self, group, i, nums, per, n, k):pass# 横向遍历：考虑k个不同的桶# 设置桶的索引为j，横向遍历每一个桶for j in range(k):# 如果当前桶的和group[j]和前一个桶的和group[j-1]相等# 则无需考虑当前桶的更新，进行剪枝if j != 0 and group[j] == group[j-1]:continue# 状态更新：将nums[i]放入第j个桶中，# 也就是将nums[i]加到group[j]中group[j] += nums[i]# 纵向遍历，考虑下一个数字，也就是将i+1传入dfs函数中并调用# 只有当if group[j] <= per:self.dfs(group, i+1, nums, per, n, k)# 状态回滚：将nums[i]从第j个桶中拿出# 也就是group[j]减去nums[i]group[j] -= nums[i]

加上了这两个剪枝之后，就可以顺利通过所有用例了。

与本题基本完全一致的题目有LeetCode473. 火柴拼正方形

三、参考代码

Python

class Solution:def dfs(self, group, i, nums, per, n, k):# 递归终止条件：当数组索引i到达n的时候，或者已经找到了一组正确的分配# 说明整个回溯完成，将self.ans设置为True之后，退出函数if i == n or self.ans:self.ans = Truereturn# 横向遍历：考虑k个不同的桶# 设置桶的索引为j，横向遍历每一个桶for j in range(k):# 如果当前桶的和group[j]和前一个桶的和group[j-1]相等# 则无需考虑当前桶的更新，进行剪枝if j != 0 and group[j] == group[j-1]:continue# 状态更新：将nums[i]放入第j个桶中，# 也就是将nums[i]加到group[j]中group[j] += nums[i]# 纵向遍历，考虑下一个数字，也就是将i+1传入dfs函数中并调用if group[j] <= per:self.dfs(group, i+1, nums, per, n, k)# 状态回滚：将nums[i]从第j个桶中拿出# 也就是group[j]减去nums[i]group[j] -= nums[i]def canPartitionKSubsets(self, nums: List[int], k: int) -> bool:# 计算所有数字nums的和totaltotal = sum(nums)# 如果total不能整除k，直接返回Falseif total % k != 0:return False# 当total可以整除k时，计算各个桶最终到达的和perper = total // k# 贪心地对nums进行逆序排序，减少遍历次数nums.sort(reverse = True)# 如果nums中的最大值已经大于per# 那么也一定无法完成分配if nums[0] > per:return Falsen = len(nums)# 初始化成员变量self.ans为Falseself.ans = False# 初始化长度为k的group数组，表示k个桶的求和情况group = [0] * k# 递归入口：传入i=0，表示nums[0]开始填入桶中self.dfs(group, 0, nums, per, n, k)# 返回self.ans的值来表示是否找到了答案return self.ans

Java

public class Solution {private boolean ans = false; // 记录是否找到答案public void dfs(int[] group, int i, int[] nums, int per, int n, int k) {// 递归终止条件：当数组索引 i 到达 n 或者已经找到了一组正确的分配if (i == n || ans) {ans = true;return;}// 横向遍历：考虑 k 个不同的桶for (int j = 0; j < k; j++) {// 剪枝：如果当前桶的和 group[j] 和前一个桶的和 group[j-1] 相等，则无需重复计算if (j != 0 && group[j] == group[j - 1]) {continue;}// 状态更新：将 nums[i] 放入第 j 个桶group[j] += nums[i];// 纵向遍历，考虑下一个数字if (group[j] <= per) {dfs(group, i + 1, nums, per, n, k);}// 状态回滚：将 nums[i] 从第 j 个桶中拿出group[j] -= nums[i];}}public boolean canPartitionKSubsets(int[] nums, int k) {// 计算所有数字 nums 的和 totalint total = Arrays.stream(nums).sum();// 如果 total 不能整除 k，直接返回 falseif (total % k != 0) {return false;}// 计算每个桶的目标和 perint per = total / k;// 贪心地对 nums 进行逆序排序，减少遍历次数Arrays.sort(nums);int n = nums.length;for (int i = 0, j = n - 1; i < j; i++, j--) {int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}// 如果 nums 中的最大值大于 per，则无法完成分配if (nums[0] > per) {return false;}// 初始化成员变量 ansans = false;// 初始化 k 个桶的求和情况int[] group = new int[k];// 递归入口dfs(group, 0, nums, per, n, k);// 返回是否找到答案return ans;}
}

C++

class Solution {
private:bool ans = false; // 记录是否找到答案public:void dfs(vector<int>& group, int i, vector<int>& nums, int per, int n, int k) {// 递归终止条件：当数组索引 i 到达 n 或者已经找到了一组正确的分配if (i == n || ans) {ans = true;return;}// 横向遍历：考虑 k 个不同的桶for (int j = 0; j < k; j++) {// 剪枝：如果当前桶的和 group[j] 和前一个桶的和 group[j-1] 相等，则无需重复计算if (j != 0 && group[j] == group[j - 1]) {continue;}// 状态更新：将 nums[i] 放入第 j 个桶group[j] += nums[i];// 纵向遍历，考虑下一个数字if (group[j] <= per) {dfs(group, i + 1, nums, per, n, k);}// 状态回滚：将 nums[i] 从第 j 个桶中拿出group[j] -= nums[i];}}bool canPartitionKSubsets(vector<int>& nums, int k) {// 计算所有数字 nums 的和 totalint total = accumulate(nums.begin(), nums.end(), 0);// 如果 total 不能整除 k，直接返回 falseif (total % k != 0) {return false;}// 计算每个桶的目标和 perint per = total / k;// 贪心地对 nums 进行逆序排序，减少遍历次数sort(nums.rbegin(), nums.rend());// 如果 nums 中的最大值大于 per，则无法完成分配if (nums[0] > per) {return false;}// 初始化成员变量 ansans = false;// 初始化 k 个桶的求和情况vector<int> group(k, 0);// 递归入口dfs(group, 0, nums, per, nums.size(), k);// 返回是否找到答案return ans;}
};

C

bool ans = false; // 记录是否找到答案// 递归回溯函数
void dfs(int* group, int i, int* nums, int per, int n, int k) {// 递归终止条件：当数组索引 i 到达 n 或者已经找到了一组正确的分配if (i == n || ans) {ans = true;return;}// 横向遍历：考虑 k 个不同的桶for (int j = 0; j < k; j++) {// 剪枝：如果当前桶的和 group[j] 和前一个桶的和 group[j-1] 相等，则无需重复计算if (j != 0 && group[j] == group[j - 1]) {continue;}// 状态更新：将 nums[i] 放入第 j 个桶group[j] += nums[i];// 纵向遍历，考虑下一个数字if (group[j] <= per) {dfs(group, i + 1, nums, per, n, k);}// 状态回滚：将 nums[i] 从第 j 个桶中拿出group[j] -= nums[i];}
}// 比较函数，用于 `qsort` 进行降序排序
int cmp(const void* a, const void* b) {return (*(int*)b - *(int*)a);
}// LeetCode 格式的函数
bool canPartitionKSubsets(int* nums, int numsSize, int k) {// 计算所有数字 nums 的总和 totalint total = 0;for (int i = 0; i < numsSize; i++) {total += nums[i];}// 如果 total 不能整除 k，直接返回 falseif (total % k != 0) {return false;}// 计算每个桶的目标和 perint per = total / k;// 对 nums 进行降序排序，减少遍历次数qsort(nums, numsSize, sizeof(int), cmp);// 如果 nums 中的最大值大于 per，则无法完成分配if (nums[0] > per) {return false;}// 初始化全局变量 ansans = false;// 初始化 k 个桶的求和情况int* group = (int*)calloc(k, sizeof(int));// 递归入口dfs(group, 0, nums, per, numsSize, k);// 释放动态分配的内存free(group);// 返回是否找到答案return ans;
}

JavaScript

/*** @param {number[]} nums* @param {number} k* @return {boolean}*/
var canPartitionKSubsets = function(nums, k) {let total = nums.reduce((acc, val) => acc + val, 0);// 如果总和不能整除 k，则无法分割if (total % k !== 0) {return false;}const per = total / k; // 每个子集的目标和nums.sort((a, b) => b - a); // 降序排序，减少搜索空间// 如果最大值已经大于目标和，直接返回 falseif (nums[0] > per) {return false;}let ans = false;let group = new Array(k).fill(0); // 用于存储 k 个桶的当前求和情况/*** 递归回溯* @param {number} i 当前处理的索引*/function dfs(i) {// 递归终止条件：当所有数字都被分配，或者已找到有效解if (i === nums.length || ans) {ans = true;return;}for (let j = 0; j < k; j++) {// 剪枝：如果当前桶的和 group[j] 和前一个桶的和 group[j-1] 相等，则无需重复计算if (j !== 0 && group[j] === group[j - 1]) {continue;}// 尝试将 nums[i] 放入桶 jgroup[j] += nums[i];// 只有当 group[j] 不超过目标值时，继续递归if (group[j] <= per) {dfs(i + 1);}// 状态回溯：撤销 nums[i] 放入桶 jgroup[j] -= nums[i];}}dfs(0);return ans;
};

Go

// 递归回溯函数
func dfs(group []int, i int, nums []int, per int, n int, k int, ans *bool) {// 递归终止条件：当数组索引 i 到达 n 或者已经找到了一组正确的分配if i == n || *ans {*ans = truereturn}// 横向遍历：考虑 k 个不同的桶for j := 0; j < k; j++ {// 剪枝：如果当前桶的和 group[j] 和前一个桶的和 group[j-1] 相等，则无需重复计算if j != 0 && group[j] == group[j-1] {continue}// 状态更新：将 nums[i] 放入第 j 个桶group[j] += nums[i]// 纵向遍历，考虑下一个数字if group[j] <= per {dfs(group, i+1, nums, per, n, k, ans)}// 状态回滚：将 nums[i] 从第 j 个桶中拿出group[j] -= nums[i]}
}// 核心函数：判断是否能将数组划分为 k 个子集，每个子集的和相等
func canPartitionKSubsets(nums []int, k int) bool {// 计算所有数字 nums 的总和 totaltotal := 0for _, num := range nums {total += num}// 如果 total 不能整除 k，直接返回 falseif total%k != 0 {return false}// 计算每个桶的目标和 perper := total / k// 贪心地对 nums 进行逆序排序，减少遍历次数sort.Sort(sort.Reverse(sort.IntSlice(nums)))// 如果 nums 中的最大值大于 per，则无法完成分配if nums[0] > per {return false}// 初始化答案变量 ansans := false// 初始化 k 个桶的求和情况group := make([]int, k)// 递归入口dfs(group, 0, nums, per, len(nums), k, &ans)// 返回是否找到答案return ans
}