当前位置：首页 > news >正文

算法沉淀第九天（Cinema Cashier）

news 2025/10/23 9:41:24

引言：

Cinema Cashier

题意分析

逻辑梳理

代码实现

结语：

引言：

今天是算法沉淀的第九天，因为昨天有点事，耽搁了，今天我们接着沉淀

今天我们来讲一道CF1500的题，如图

那么，话不多说，我们就进入今天的算法讲解———————>

Cinema Cashier

按照惯例，我们先来看题目

题目分析

题目如下图

这题就是告诉你有N批人想要看电影，然后电影院的大小是K *K的，然后每批人都进行判断有没有连续的位置给他们

如果有就把离中心位置最近（连座的每个座位离中心座位的距离之和）的连座分给这批人，如果有多个连座离中心位置最近，那就排数越小越好，列数也是越小越好，排数的优先级高于列数，确定完座位分配后就输出这批人座位在哪，排左列右列 这么输出

如果没有连座给他们就输出-1

直到所有批次的人全部分析完就结束程序就可以了

中心座位的座位是总行数除2后向上取整，用坐标表示即（(k+1)/2,(k+1)/2）这个位置

那么题目分析完了，接下来我们进入逻辑梳理环节

逻辑梳理

首先，第一批人安排在哪里呢，肯定是安排在中心位置的那一排，然后因为要让距离差总和最小，我们来分析俩种情况

我们先用mid表示中心位置

如果进去的人是奇数，那就是一个人坐在中心位置，其余人分俩边散开，这个时候的距离差值是最小的

如果进去的人是偶数，那就是一个人坐在中心位置，这个时候剩余的人无法使得左右人数一样多，但为了要让列尽可能小，所以左边坐的人的数量比右边坐的人的数量多一个。但是在这种情况下，我们还要进行分析，这个时候左边坐的人数量可能会超出左边的座位数，这个时候只要让他们从第一个座位开始往右坐就行了

那么，第一批的人就已经坐完了

接下来我们来想第二批的人坐哪里

这时候有哪些位置可以坐呢，首先中心位置的同列的上下俩排可以做，然后还有就是同排的俩边，如图画三角形的位置

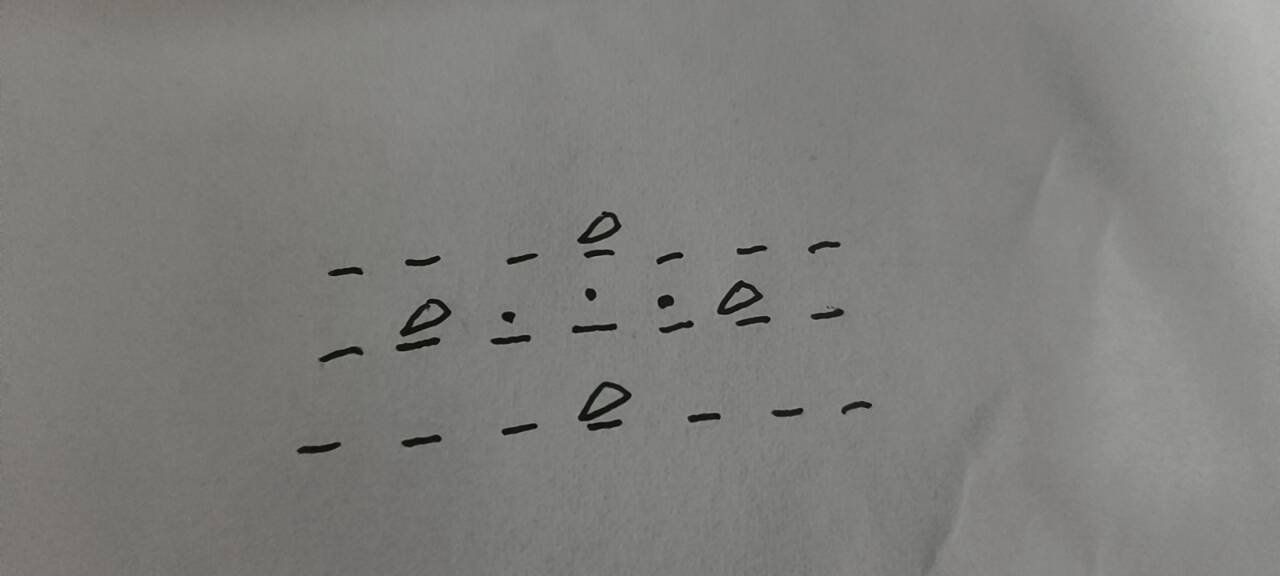
我们只需要分析这四处位置的情况，找出最适合的位置就可以了，依旧是按照上面一开始的安排位置的规则来，把每个情况都算一算，找出最小的情况，且是行最小，在行最小情况下列最小的情况就可以了，然后再对新的点进行更新就好啦

为了达到这个目的，我们可以使用2个vector数组来分别表示行和列，因为行列是一起加的，所以开俩个vector也不影响

然后因为这些情况里有可能会出现已经坐过的可能，所以我们可以把座位用vis的二维数组来标记每个位置有没有被标记过

每次判断一批人之后都用vis对座位进行更新就可以了

这题的逻辑并不难，主要是细节处理方面的问题，那么逻辑梳理完了，接下来我们进入代码实现的环节

代码实现

这里就直接放AC码啦

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <math.h>
#include <queue>
#include <map>
#include <vector>
using namespace std;int n, k;
int mid;
vector<int>X;
vector<int>Y;
bool vis[1010][1010];void solve()
{int mi = 0x3f3f3f;int m;int wei = -1;int hang = 10000;int lie = 10000;cin >> m;int x = mid - m / 2;int x1 = mid + (m - 1) / 2;for (int i = 0; i < X.size(); i++){if (vis[Y[i]][X[i]])continue;int a = 0;if (X[i] < mid){if (X[i] < m)continue;a = abs(mid - Y[i]) * m;a += (2 * mid - 2 * X[i] + m - 1) * m / 2;}else  if (X[i] > mid){if (k - X[i] + 1 < m)continue;a = abs(mid - Y[i]) * m;a += (-2 * mid + 2 * X[i] + m - 1) * m / 2;}else{a = abs(mid - Y[i]) * m;if (x <= 1){a += (mid - 1) * mid / 2 + (1 + m - mid) * (m - mid) / 2;}else{a += (mid - x) * (mid - x + 1) / 2 + (x1 - mid) * (x1 - mid + 1) / 2;}}if (a == mi){if (Y[i] == hang && X[i] < lie|| Y[i] < hang){mi = a;hang = Y[i];lie = X[i];wei = i;}}else if (a < mi){mi = a;hang = Y[i];lie = X[i];wei = i;}}if (wei == -1)cout << "-1" << endl;else{int qian = 0;int hou = 0;if (X[wei] == mid){if (x <= 1){qian = 1;hou = m;if (m != k){X[wei] = m + 1;}}else{qian = x;hou = x1;X[wei] = x - 1;X.push_back(x1 + 1);Y.push_back(Y[wei]);}if (Y[wei] - 1 > 0 && Y[wei] < mid){X.push_back(mid);Y.push_back(Y[wei] - 1);}if (Y[wei] + 1 <= k && Y[wei] > mid){X.push_back(mid);Y.push_back(Y[wei] + 1);}}else{if (X[wei] > mid){qian = X[wei];X[wei] += m;hou = X[wei] - 1;}else{hou = X[wei];X[wei] -= m;qian = X[wei] + 1;}}cout << Y[wei] << " " << qian << " " << hou << endl;for (int i = qian; i <= hou; i++)vis[Y[wei]][i] = 1;}
}int main()
{cin >> n >> k;mid = (k + 1) / 2;n--;int m;cin >> m;int x = mid - m / 2;int x1 = mid + (m - 1) / 2;if (x <= 1){cout << mid << " 1 " << m << endl;if (m != k){X.push_back(m + 1);Y.push_back(mid);}}else{cout << mid << " " << x << " " << x1 << endl;X.push_back(x - 1);Y.push_back(mid);X.push_back(x1 + 1);Y.push_back(mid);}if (mid - 1 > 0){X.push_back(mid);Y.push_back(mid - 1);}if (mid + 1 <= k){X.push_back(mid);Y.push_back(mid + 1);}while (n--){solve();}return 0;
}