当前位置：首页 > news >正文

双目测距实战5-立体矫正

news 2025/10/23 9:40:08

注：本文参考课件来自CMU
代码参考：https://github.com/Liwx1014/HikDualCamera_Stereo/blob/main/stereo_rectification.py

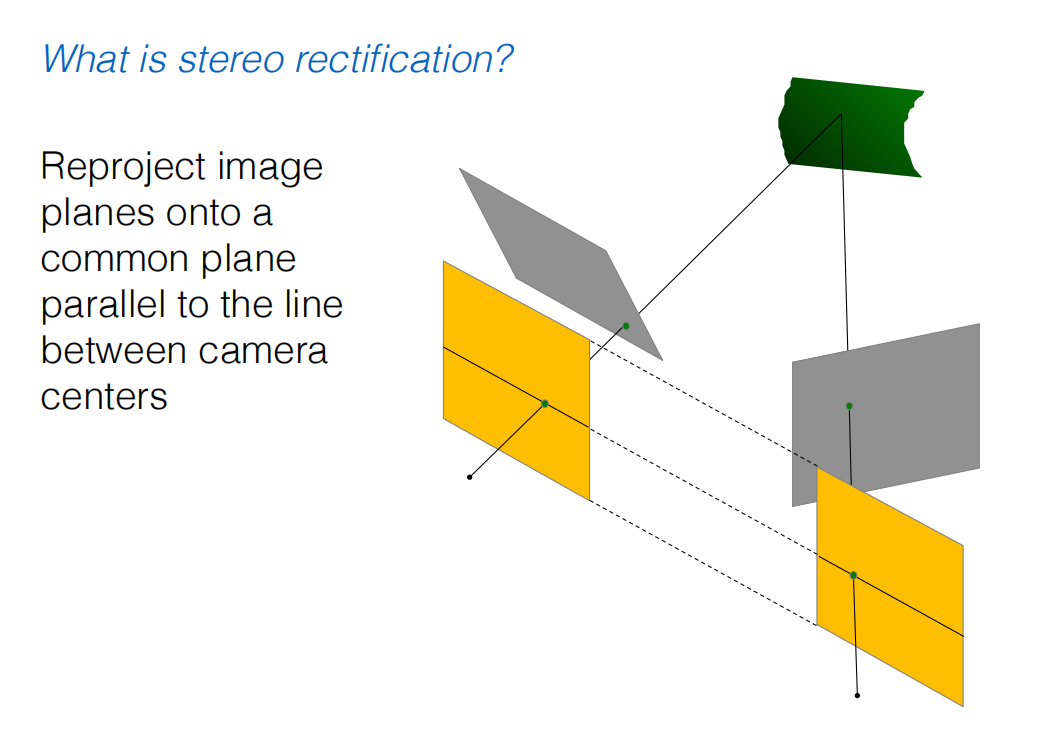
什么是立体矫正

立体矫正的前提条件

为了实现几何上最精确、最理想的立体矫正（如课件中描述的流程），前提条件是需要知道两个相机的内参。
即使完全不知道内外参数，也有一种方法可以进行矫正，尽管其结果在几何意义上不那么“纯粹”。

情况一：已校准的相机 (Calibrated Case) - 需要内参

这正是CMU课件中隐含的标准流程。

需要什么参数？
- 内参矩阵 K (Intrinsic Matrix)：你必须知道两个相机各自的内参矩阵 K。这个矩阵包含了相机的焦距 (fx, fy)、主点坐标 (cx, cy) 和像素的倾斜因子。这些参数通常通过一次性的相机标定过程（例如使用棋盘格）来获得。
为什么需要内参？
- 为了计算基础矩阵 E (Essential Matrix)：矫正流程的第一步是计算 E。E 矩阵的定义是建立在归一化图像坐标系下的，这个坐标系是一个与像素无关的、以米为单位的度量空间。要将像素坐标 (u, v) 转换到归一化坐标，就必须使用内参矩阵 K 的逆矩阵：x_normalized = K⁻¹ * x_pixel。
- 为了进行精确的分解：只有从 E 矩阵分解，才能得到真实的、具有物理意义的相对旋转矩阵 R 和（单位化的）平移向量 T。这些都是三维欧几里得空间中的变换。
- 为了生成最终的变换：在最后一步应用变换时，我们计算的单应性矩阵 H = K * R_rect * K⁻¹ 也依赖于 K。这个变换确保了矫正过程是一个纯粹的“虚拟相机旋转”，能够保持场景的几何结构（例如直线仍然是直线）。
流程总结 (已校准)：
像素点 -> (需要 K) -> 归一化点 -> (8点法) -> E矩阵 -> (分解) -> R, T, R_rect -> (需要 K) -> 最终矫正图像

所以，在这种最标准、效果最好的方法中，内参是绝对必要的。而外参（两个相机间的相对R和T）是作为流程的一部分被计算出来的，你不需要提前知道。

情况二：未校准的相机 (Uncalibrated Case) - 可以不需要内外参

如果你的相机没有经过标定，完全不知道内参 K 怎么办？还能进行矫正吗？

答案是：可以，但我们处理的对象不再是 E 矩阵。

核心变成基本矩阵 F (Fundamental Matrix)：
- 在不知道内参的情况下，八点法计算出的不再是 E 矩阵，而是基本矩阵 F。F 矩阵直接关联两个视图的像素坐标，它的约束方程是 x'_pixelᵀ * F * x_pixel = 0。
- F 和 E 的关系是 F = K'⁻ᵀ * E * K⁻¹。可以看到，F 包含了 E (几何关系) 和 K, K' (相机内部投影特性) 的所有信息。
如何用 F 进行矫正？
- 即使只有 F，我们仍然可以计算出极点 e (通过求解 Fe = 0)。
- 既然有了极点，我们就可以构建一个投影变换矩阵 H (而不是一个纯粹的旋转矩阵)，这个变换同样可以将极点 e 映射到无穷远处 (1, 0, 0)。
- 将这个投影变换 H 应用于两幅图像，同样可以使极线变成水平。
这种方法的优缺点是什么？
- 优点：非常灵活，你不需要对相机进行任何预先的标定。只要能找到8对以上的匹配点，就能完成矫正。
- 缺点：
  - 产生投影畸变：因为应用的变换 H 是一个普适的投影变换，它不保证是纯粹的旋转。因此，矫正后的图像可能会出现更多的透视畸变。例如，图像中的正方形可能不再是正方形。
  - 无法恢复真实尺度：从 F 无法直接分解出度量意义上的 R 和 T。因此，后续计算出的视差图，虽然可以反映深度的相对关系，但很难恢复出具有真实物理单位（如米）的深度值。

结论与总结

特性	已校准方法 (使用 E)	未校准方法 (使用 F)
核心矩阵	基础矩阵 (Essential Matrix) `E`	基本矩阵 (Fundamental Matrix) `F`
前提条件	需要两个相机的内参矩阵 K	不需要任何相机参数 (只需要点匹配)
计算对象	归一化图像坐标	像素坐标
矫正变换类型	纯旋转 (欧几里得变换)	投影变换 (Homography)
矫正后图像质量	几何失真小，更“自然”	可能引入更多透视畸变
后续应用	可进行度量三维重建	主要用于计算视差，进行相对深度估计

总而言之，要实现课件中那种高质量、几何精确的立体矫正，前提就是已经通过相机标定获取了两个相机的内参矩阵 K。 这是在学术研究和工业应用（如自动驾驶、高精度测量）中的首选方法。

立体矫正的总体目标

在开始之前，我们再次明确立体矫正目标：通过对两幅原始图像进行透视变换（主要是旋转），生成两幅新的、经过矫正的图像。在新图像中，任何一个3D点在两幅图上的投影都位于同一水平线上。

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传
上图：未校正，对应点不匹配。右图：矫正后的图像对，所有对应点都位于水平的极线上。

立体矫正算法详解

第一步：估算基础矩阵 E (Estimate E)

任务: 找到描述两个摄像头坐标系之间几何关系的基础矩阵E (Essential Matrix)。
原理: 基础矩阵 E 是一个3x3的矩阵，它蕴含了两个摄像头之间的全部相对位姿信息，即旋转矩阵 R 和 平移向量 T。它通过一个被称为极线约束的核心方程 x'^T * E * x = 0 来连接左右图像中的对应点 x 和 x'。
方法: 如课件所述，通常使用 “八点法” (8-point algorithm)。你需要从两张图片中找出至少8对可靠的匹配点。将这8对点的坐标代入极线约束方程，你就能得到一个线性方程组。通过奇异值分解 (SVD) 求解这个方程组，可以得到最符合所有匹配点的基础矩阵 E。SVD在这里的作用是找到在有噪声情况下最稳健的解。
输入: 至少8对在左右图像中匹配的像素点坐标。
输出: 3x3的基础矩阵 E。

第二步：估算极点 e (Estimate the epipole e)

任务: 找到极点 e。极点是一个摄像头的光心在另一个摄像头成像平面上的投影。它是所有极线的汇聚点。
原理: 根据基础矩阵的定义，极点 e 位于 E 的零空间中，满足方程 Ee = 0。我们的目标是把这个点“推”到无穷远处，从而让所有汇聚于此的极线变得相互平行。
方法: 同样地，通过对 E 进行奇异值分解 (SVD)，可以非常容易地找到它的零空间，从而解出极点 e 的坐标。
输入: 基础矩阵 E。
输出: 极点向量 e。

第三步：根据极点 e 构建矫正旋转矩阵 R_rect (Build R_rect from e)

任务: 这是矫正过程的核心。我们需要构建一个旋转矩阵 R_rect，它能将当前的摄像头坐标系旋转到一个新的、“已矫正”的坐标系。在这个新坐标系里，原来的极点 e 会被旋转到 (1, 0, 0) 方向，也就是新的X轴的无穷远处。
原理与方法 (参考课件第42页):
1. 定义新的X轴 (r₁): 让新的X轴方向直接指向原来的极点方向。因此，r₁ 就是单位化的极点向量 e。r₁ = e / ||e||。
2. 定义新的Y轴 (r₂): 新的Y轴必须与新的X轴 r₁ 垂直。一个巧妙的构造方法是取 r₁ 与原始坐标系Z轴（通常是光轴方向 [0, 0, 1]^T）的叉乘。这会产生一个同时垂直于 r₁ 和原始Z轴的向量，确保了新的Y轴是水平的。
3. 定义新的Z轴 (r₃): 新的Z轴必须同时垂直于新的X轴和Y轴。通过计算 r₃ = r₁ × r₂ 即可得到，这样 (r₁, r₂, r₃) 就构成了一个标准正交基（一个旋转矩阵的行或列）。
输入: 极点向量 e。
输出: 3x3的矫正旋转矩阵 R_rect。

第四步：将 E 分解为 R 和 T (Decompose E into R and T)

任务: 从我们第一步得到的基础矩阵 E 中，分解出原始两个摄像头之间的相对旋转矩阵R和平移向量T。
原理: 基础矩阵 E 本身是由 R 和 T 构成的 (E = [T]_× R)。通过对 E 进行SVD，可以反解出 R 和 T。需要注意的是，分解会产生四组可能的 (R, T) 解，你需要通过一些额外的几何约束（例如，将一个3D点投影到两个相机中，确保它在两个相机的前方）来确定唯一正确的解。
输入: 基础矩阵 E。
输出: 原始的相对旋转矩阵 R 和平移向量 T。

第五步：设置左右相机的最终矫正矩阵 (Set R₁ and R₂)

任务: 确定最终要应用到左右两幅图像上的总旋转量。
原理:
- 左相机: 它只需要进行矫正旋转即可。所以，左相机的最终旋转矩阵 R₁ = R_rect。
- 右相机: 为了与矫正后的左相机对齐，右相机需要进行两步旋转：首先，它需要应用原始的相对旋转 R 来和左相机的原始姿态对齐；然后，再和左相机一样，应用矫得旋转 R_rect。因此，右相机的最终旋转矩阵 R₂ = R_rect * R。
输入: R_rect 和 R。
输出: 左相机的矫正矩阵 R₁ 和右相机的矫正矩阵 R₂。

第六、七、八步：应用变换，生成新图像 (Warp images)

任务: 将原始图像的每个像素根据 R₁ 和 R₂ 变换到新的矫正图像平面上。这个过程也叫图像 warping。
原理: 我们不能简单地移动像素。正确的做法是：
1. 创建一个空白的矫正后图像。
2. 遍历新图像中的每一个像素 p'。
3. 将这个像素 p' 的坐标通过其对应的逆旋转矩阵 (R₁⁻¹ 或 R₂⁻¹) 变换回原始相机的坐标系中。
4. 将变换后的坐标投影到原始图像上，找到对应的源像素 p。
5. 由于 p 的坐标很可能不是整数，需要使用双线性插值等方法来计算其精确的颜色值。
6. 将这个颜色值赋给新图像的像素 p'。
方法 (更实用): 如课件第47页所述，这个过程在实践中通常通过计算一个单应性矩阵 H (Homography Matrix) 来完成。对于左相机，H₁ = K * R₁ * K⁻¹，其中 K 是相机的内参矩阵。这个 H₁ 矩阵可以直接将原始左图的像素坐标映射到矫正后左图的像素坐标。对右相机也同理 (H₂ = K * R₂ * K⁻¹)。然后使用这个单应性矩阵来“扭曲”原始图像，生成矫正后的图像。
输入: 原始左右图像，R₁，R₂，以及相机内参矩阵 K。
输出: 两幅已经过立体矫正的、极线水平对齐的新图像。

完成以上所有步骤后，我们就得到了一对理想的立体图像，可以非常高效地进行下一步的立体匹配 (Stereo Matching)，从而计算出密集的深度图。

当对原始左右图像进行立体矫正后，实际上是创建了一个新的、理想化的虚拟立体相机。在这个虚拟系统中，左右两个相机的是平行的，成像平面是共面的。两个虚拟相机的内参矩阵变得完全相同，基线则在物体世界中定义，两个原始相机之间的光心距离，这个值在矫正中不会改变，通常从平移向量中计算而来。

工程实践-如何处理不完美

处理不完美的矫正（即存在垂直偏移）是工程实践中必须面对的挑战。一个鲁棒的双目测距系统不会假设矫正是完美的，而是会建立一套“多层防御”体系来应对这个问题。

以下是在整个双目测距流程中，从前到后可以采取的改进措施，分为预防、适应、修复三个层次。

层次一：预防——从根源上最小化垂直偏移

这是最重要、最有效的一步。与其下游补救，不如上游根治。

进行超高精度的相机标定：
- 增加标定图像数量和质量：使用几十张甚至上百张清晰、光照均匀、无运动模糊的图像。确保标定板出现在视野的各个角落和不同深度，因为镜头畸变在图像边缘最严重。
- 使用高精度标定板：确保标定板本身是平的，打印精度高。
- 优化畸变模型：除了标准的5个畸变参数(k1, k2, p1, p2, k3)，可以考虑使用包含更高阶径向畸变(k4, k5, k6)的模型，特别是对于广角镜头，这能显著减少边缘的残余畸变。
- 全局优化 (Bundle Adjustment)：使用“光束法平差”来同时优化所有内外参，最小化全局重投影误差，这能得到最一致、最精确的参数。
保证硬件平台的刚性与同步：
- 刚性连接：使用坚固的金属支架固定两个相机，并在设计上考虑抗振动和热胀冷缩，确保它们的相对位姿在标定后不会改变。
- 硬件同步：必须使用硬件触发来保证两个相机的快门在微秒级别上同步。对于动态场景，任何不同步都会引入额外的、看似垂直偏移的误差。

层次二：适应——让立体匹配算法更“宽容”

即使做到了最好的预防，微小的误差（例如0.5个像素）可能依然存在。下一步是让核心的立体匹配算法能够容忍这些误差。

对于传统算法 (如SGM, Block Matching)：
- 二维搜索窗口：这是最核心的改进。放弃严格的1D水平线搜索，改为在一个小的2D矩形区域内搜索。
- 具体实现：对于左图的点(x, y)，在右图的搜索区域从 [x_min, x_max] 的一条线，扩展为 [x_min, x_max] × [y - N, y + N] 的一个矩形。
- N的取值：N是你预估的最大垂直偏移量，通常设为1或2个像素。设置得太大，会急剧增加计算成本和误匹配的概率；设置得太小，则无法容忍误差。这是一个需要权衡的参数。
- 代价：计算复杂度会乘以 (2N+1) 倍，对实时性是巨大挑战。
对于深度学习算法 (如RAFT-Stereo)：
- 模型微调 (Finetuning)：这是非常有效的方法。创建一个包含不完美矫正的合成数据集。你可以通过对完美矫正的图像对施加一个微小的、随机的垂直仿射变换来模拟垂直偏移。然后，用这个新的“有噪声”的数据集对预训练好的模型进行微调。网络会学会对这种微小的垂直偏移变得不敏感。
- 修改网络结构：更高级的方法是修改网络结构，例如将相关性查询从1D（沿水平线）扩展到局部2D区域。但这需要对模型本身进行深入修改，难度较高。

层次三：修复——后处理阶段识别并剔除错误

匹配完成后，由垂直偏移导致的错误匹配通常会表现为一些“异常值”。我们可以通过后处理手段来识别和修复它们。

强化左右一致性检查 (Left-Right Consistency Check)：
- 这是对抗不完美矫正的最强防线。一个因垂直偏移产生的错误匹配，几乎不可能在反向检查中也得到一致的结果。
- 因此，当存在垂直偏移风险时，必须执行左右一致性检查，并将不一致的点标记为无效。
引入唯一性约束 (Uniqueness Constraint)：
- 在匹配成本计算中，如果最佳匹配成本与次优匹配成本非常接近，说明这个匹配是模糊的、不可靠的。这在重复纹理区域很常见，也可能由垂直偏移导致。
- 设定一个阈值，如果 (cost_second_best / cost_best) < threshold，则认为该匹配有效，否则视为无效。
使用更智能的滤波和空洞填充：
- 剔除小连通域 (Speckle Filtering)：由错误匹配产生的视差区域通常是孤立的小噪点。可以剔除掉所有面积小于某个阈值的连通区域。
- 边缘保持滤波：在剔除大量无效点后，视差图上会出现很多“空洞”。使用边缘保持的滤波算法，如加权中值滤波或引导滤波 (Guided Filter)，利用原始彩色图像的边缘信息来智能地填充这些空洞。

高级策略：在线自校准

对于那些硬件无法保证长期稳定（如车载、无人机）的系统，最先进的解决方案是：

在线自校准 (Online Self-Calibration)：系统在运行过程中，持续地跟踪稀疏特征点（如ORB, SIFT）。通过分析大量特征点的长期运动，可以反向推断出相机外参（R和T）是否发生了微小的漂移。如果检测到漂移，系统可以动态地更新矫正矩阵，从而实时补偿硬件变化带来的误差。这本质上是一个简化的视觉SLAM（同步定位与建图）过程。