贪心 --- 前篇

算法简介
贪心算法(Greedy Algorithm)是一种在每一步决策中都采取当前状态下最优(即最有利)的选择,从而希望导致结果是全局最优的算法策略。
核心思想
它不考虑整体最优解,而是通过一系列局部最优选择(“贪心选择”)来构建全局解。其关键在于:每一步的选择只依赖于当前状态,且一旦做出选择就不再回溯。
适用场景
贪心算法并非适用于所有问题,其有效性依赖于问题是否满足两个核心性质:
- 贪心选择性质:全局最优解可以通过一系列局部最优选择(贪心选择)来获得。即,每次选择的局部最优解能逐步累积成全局最优解。
- 最优子结构性质:问题的最优解包含子问题的最优解。当一个问题的最优解可以由其子问题的最优解推导而来时,该问题具有最优子结构。
优点与局限
- 优点:实现简单、效率高(通常是线性或线性对数时间复杂度),适合解决具有明确贪心选择性质的问题。
- 局限:不能保证对所有问题都得到全局最优解(可能陷入局部最优),因此需严格证明问题满足贪心选择性质后再使用。
典型应用
- 活动选择问题(最大化可参加的活动数量)
- 哈夫曼编码(数据压缩中的最优编码方式)
- 最短路径问题(Dijkstra 算法)
- 最小生成树(Kruskal 算法、Prim 算法)
- 零钱兑换问题(当货币面额满足特定条件时,如美元、人民币的硬币面额)
贪心算法的核心是 “做出当下最好的选择”,其有效性的关键在于问题性质的适配性,实际应用中需结合具体问题分析是否适用。

题目练习
860. 柠檬水找零 - 力扣(LeetCode)
解法(贪心):
贪心策略:
通过分情况讨论,根据收到的钱的面额,选择最优的找零方式,确保能顺利找零。
遇到 5 元钱:直接收下,因为不需要找零,且 5 元是基础找零单位;
遇到 10 元钱:找零 1 张 5 元后收下,这样既完成了当前的找零,又保留了合理的零钱组合;
遇到 20 元钱:
- 优先尝试用 1 张 10 元 + 1 张 5 元的组合找零,因为 10 元的使用能减少后续找零对 5 元的依赖;
- 若凑不出 10 + 5 的组合,再用 3 张 5 元的组合找零。
class Solution {
public:bool lemonadeChange(vector<int>& bills) {int five = 0, ten = 0;for(const auto x : bills) {if(x == 5) ++five;else if(x == 10) {if(five == 0) return false;++ten; --five;}else {if(ten && five) {--ten; --five;}else if(five >= 3) five -= 3;else return false;}}return true;}
};
2208. 将数组和减半的最少操作次数 - 力扣(LeetCode)
解法(贪心):
贪心策略:
- a. 每次挑选出「当前」数组中「最大」的数,然后「减半」;
- b. 直到数组和减少到至少一半为止。
为了「快速」挑选出数组中最大的数,我们可以利用「堆」这个数据结构。

class Solution {
public:int halveArray(vector<int>& nums) {priority_queue<double> heap;double sum = 0, ret = 0;for(auto x : nums) {sum += x;heap.push(x);}double tmp = sum / 2;while(sum > tmp) {++ret;double t = heap.top(); heap.pop();heap.push(t / 2); sum -= t / 2;}return ret;}
};
179. 最大数 - 力扣(LeetCode)
解法(贪心):
可以先优化:
将所有的数字当成字符串处理,那么两个数字之间的拼接操作以及比较操作就会很方便。
贪心策略:
按照题目的要求,重新定义一个新的排序规则,然后排序即可。
排序规则:
- a. 「A 拼接 B」大于「B 拼接 A」,那么A 在前,B 在后;
- b. 「A 拼接 B」等于「B 拼接 A」,那么A、B 的顺序无所谓;
- c. 「A 拼接 B」小于「B 拼接 A」,那么B 在前,A 在后;

class Solution {
public:string largestNumber(vector<int>& nums) {vector<string> strs;for(auto x : nums) {strs.push_back(to_string(x));}sort(strs.begin(), strs.end(), [](const string& s1, const string& s2){return s1 + s2 > s2 + s1;});string ret;for(auto str : strs) ret += str;if(ret[0] == '0') return "0";return ret;}
};
376. 摆动序列 - 力扣(LeetCode)
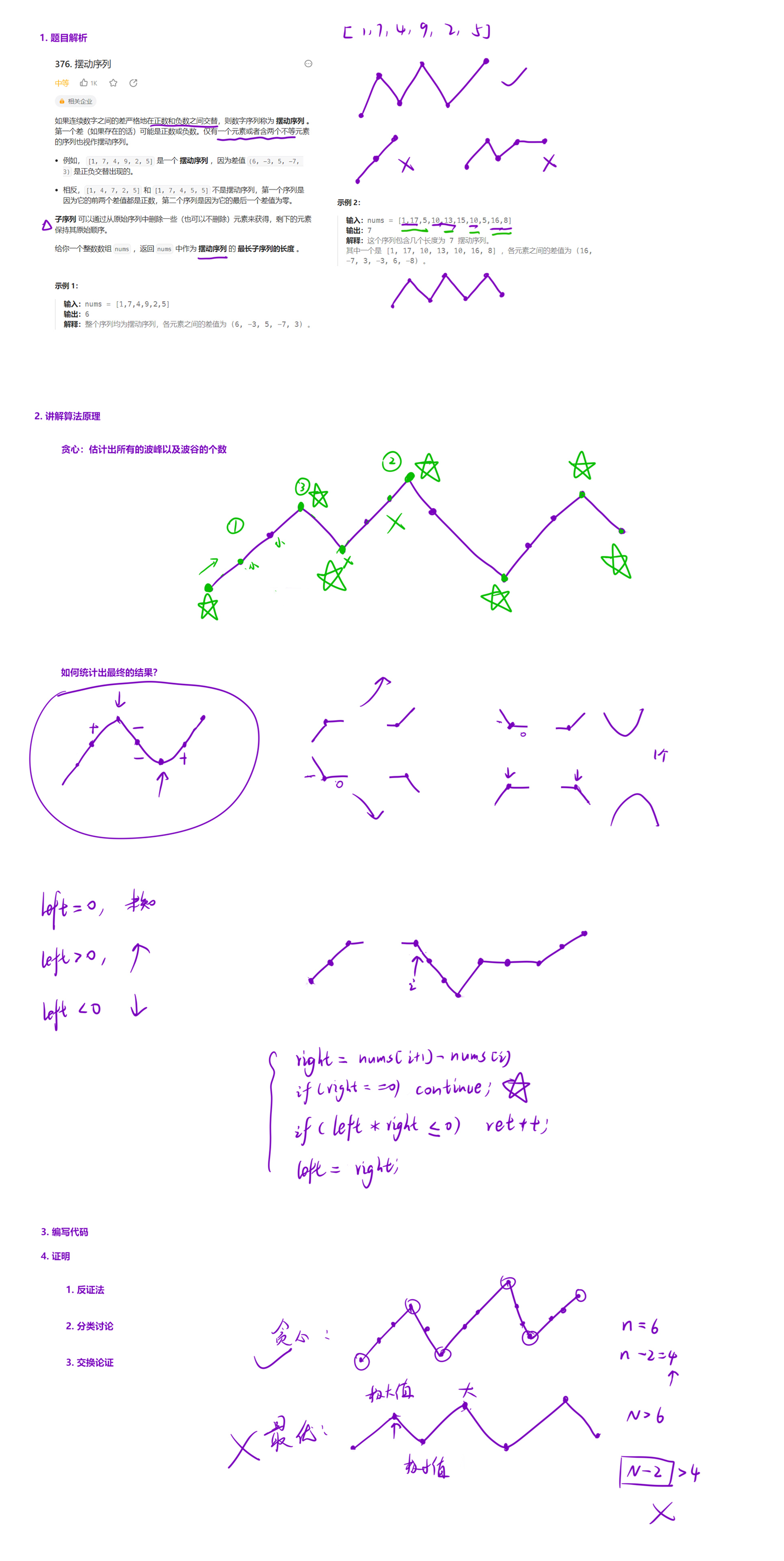
class Solution {
public:int wiggleMaxLength(vector<int>& nums) {int n = nums.size();if(n < 2) return n;int left = 0, ret = 0;for(int i = 0; i < n - 1; ++i) {int right = nums[i + 1] - nums[i];if(right == 0) continue;if(left * right <= 0) ++ret;left = right;}return ret + 1;}
};
300. 最长递增子序列 - 力扣(LeetCode)
解法(贪心):
贪心策略:
我们在考虑最长递增子序列的长度的时候,其实并不关心这个序列长什么样子,我们只是关心最后一个元素是谁。这样新来一个元素之后,我们就可以判断是否可以拼接到它的后面。
因此,我们可以创建一个数组,统计长度为 x 的递增子序列中,最后一个元素是谁。为了尽可能让这个序列更长,我们仅需统计长度为 x 的所有递增序列中最后一个元素的 「最小值」。
统计的过程中发现,数组中的数呈现 「递增」趋势,因此可以使用「二分」 来查找插入位置。

class Solution {
public:int lengthOfLIS(vector<int>& nums) {vector<int> ret;ret.push_back(nums[0]);int n = nums.size();for(int i = 1; i < n; ++i) {int tmp = nums[i];if(tmp > ret.back()) ret.push_back(tmp);else {int left = 0, right = ret.size() - 1;while(left < right) {int mid = left + ((right - left) >> 1);if(ret[mid] < tmp) left = mid + 1;else right = mid;}ret[left] = tmp;}}return ret.size();}
};
334. 递增的三元子序列 - 力扣(LeetCode)
解法(贪心):
贪心策略:
这是最长递增子序列的简化版。
- 无需用数组存储数据,仅需两个变量即可;
- 也不用二分查找插入位置,仅需两次比较就能确定插入位置。

class Solution {
public:bool increasingTriplet(vector<int>& nums) {int n = nums.size(), a = nums[0], b = INT_MAX;for(int i = 1; i < n; ++i) {if(nums[i] > b) return true;else if(nums[i] > a) b = nums[i];else a = nums[i];}return false;}
};
674. 最长连续递增序列 - 力扣(LeetCode)
解法(贪心):
贪心策略:
找到以某个位置为起点的最长连续递增序列之后(设这个序列的末尾为 j 位置),接下来直接以 j + 1 的位置为起点寻找下一个最长连续递增序列。

class Solution {
public:int findLengthOfLCIS(vector<int>& nums) {int ret = 0, n = nums.size();for(int i = 0; i < n;) {int j = i + 1;while(j < n && nums[j] > nums[j - 1]) ++j;ret = max(j - i, ret);i = j;}return ret;}
};
121. 买卖股票的最佳时机 - 力扣(LeetCode)
解法(贪心):
贪心策略:
由于只能交易一次,所以对于某一个位置 i,要想获得最大利润,仅需知道前面所有元素的最小值。然后在最小值的位置「买入」股票,在当前位置「卖出」股票即可。

class Solution {
public:int maxProfit(vector<int>& prices) {int premin = prices[0], ret = 0, n = prices.size();for(int cur = 1; cur < n; ++cur) {ret = max(ret, prices[cur] - premin);premin = min(prices[cur], premin);}return ret;}
};
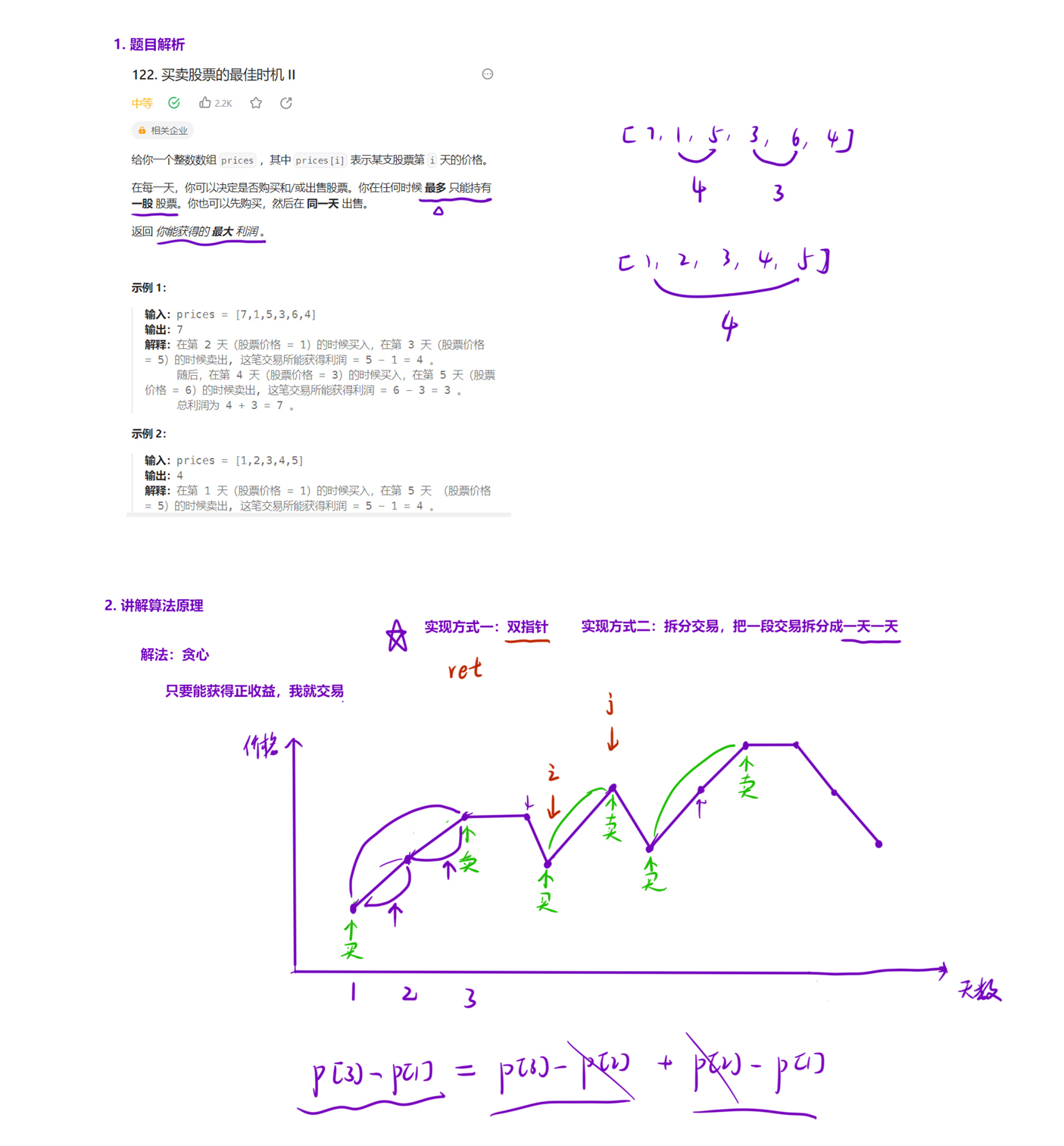
122. 买卖股票的最佳时机 II - 力扣(LeetCode)
解法(贪心):
贪心策略:
由于可以进行无限次交易,所以只要是一个「上升区域」,我们就把利润拿到手就好了。
class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size(), ret = 0;for(int i = 0; i < n; ++i) {int j = i;while(j + 1 < n && prices[j] < prices[j + 1]) ++j;ret += prices[j] - prices[i];i = j;}return ret;}
};