牛客：矩阵消除游戏

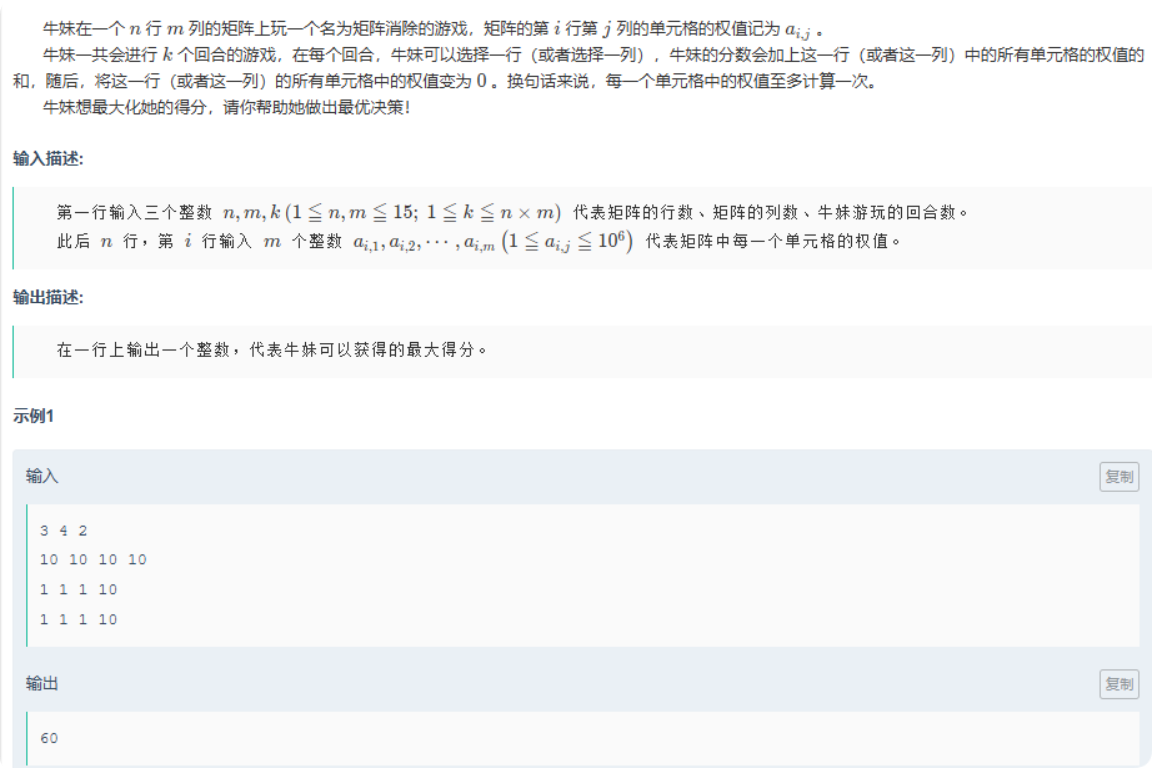
思路：由于规模在15左右，所以我们可以选择枚举（二进制枚举法（1<<n）-1）.

先选行再选列，例如：如果k=5,表示我们可以选择行列一共5次，我们可以枚举0到5行的所有选择方案，假如我们选择了3行，那么我们就把在剩下的列里面选择两个最大的，每选完5次就和之前的做比较，最后取最大的一次即可。

代码核心思路

1. 二进制枚举所有可能的选行方案：用二进制数表示选中的行（例如 101 表示选中第 1 行和第 3 行）。

2. 计算选行后的剩余可选列数：若选了 num 行，则还能选 k - num 列（需保证非负）。

3. 贪心选择最优列：对未被选中的行，计算每列的元素和，选择最大的 k - num 列，累加其和。

4. 记录最大值：遍历所有选行方案，保留总和最大的结果。

#include<bits/stdc++.h>
using namespace std; 
int n,m,k;
int num=0;
int arr[16][16]={0};
int lie[16]={0};
long long scale(int st){long long sum=0;for(int i=1;i<=n;i++){if(((st>>(i-1))&1)==1){for(int j=1;j<=m;j++){sum+=arr[i][j];}num++;}else{for(int j=1;j<=m;j++){lie[j]+=arr[i][j];}}}return sum;
}int main(){cin>>n>>m>>k;int sum=0;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>arr[i][j];sum+=arr[i][j];}}if(k>=n||k>=m){cout<<sum;return 0;}long long ans=0;for(int i=0;i<=(1<<n)-1;i++){memset(lie,0,sizeof(lie));num=0;long long sum1=scale(i);if(num>k||num<0){continue;}else{sort(lie+1,lie+m+1);int x=k-num;for(int i=1,j=m;i<=x;i++,j--){sum1+=lie[j];}ans=max(ans,sum1);}}cout<<ans;    return 0;
}