当前位置：首页 > news >正文

【研究生随笔】PyTorch中的概率论

news 2025/10/21 8:00:54

会使用到的包：

import torch as torch
from torch.distributions import multinomial

构建一个简单的概率样例：

import torch as torch
from torch.distributions import multinomial
A = torch.Tensor([1,2,3,4,5,6]) # 创建一个包含六个元素的张量，用米给后面做采样
print(multinomia1.Multinomial(1,A).samp1e()) # 意思是在张量的六个元内做一次采样
'''
输出：tensor([0.,0.,0.,1.,0.,0.])
'''

如果换成其他采样次数的话：

import torch as torch
from torch.distributions import multinomial
A = torch.Tensor([1,2,3,4,5,6]) # 创建个包含六个元系的张量，用来给后面做采样
print(multinomia1.Multinomial(6, A).sample()) # 意思是在张量的六个元素内做一次采样
'''
输出：tensor([0.,1.,0.,2.,1.,2.])
'''

然后将输出的结果除以采样次数，就可以得到相应的概率。

在给定的样本空间 S 中，事件A的概率，表⽰为 P (A)，满⾜以下属性：
○ 对于任意事件 A，其概率从不会是负数，即 P (A) ≥ 0；
○ 整个样本空间的概率为 1，即 P (S) = 1；
○ 对于互斥（mutually exclusive）（对于所有 i ≠ j 都有 A_i ∩ A_j = ∅）事件的任意⼀个可数序列 A_1，A_2…，序列中任意⼀个事件发⽣的概率等于它们各⾃发⽣的概率之和，即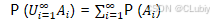
联合概率 (joint probability) P(A = a; B = b)。给定任何值 a 和 b, 联合概率可以回答, A = a和 B = b 同时满⾜的概率是多少? 请注意，对于任何 a 和 b 的取值， P(A = a; B = b) ≤ P(A = a)。这点是确定的，因为要同时发⽣ A = a 和 B = b， A = a就必须发⽣， B = b也必须发⽣（反之亦然）。因此， A = a 和B = b 同时发⽣的可能性不⼤于 A = a 或是 B = b 单独发⽣的可能性。

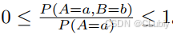
在这里插入图片描述

这个⽐率为条件概率(conditional probability)，并⽤ P(B = b j A = a) 表⽰它：它是 B = b 的概率，前提是 A = a 已发⽣。
Bayes 定理 (Bayes’theorem)。它如下所⽰。通过构造，我们有乘法规则， P(A，B) = P(B | A)P(A)。根据对称性，这也适⽤于 P(A，B) =P(A | B)P(B)。假设 P(B) > 0，求解其中⼀个条件变量，得到如下：

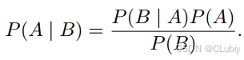
在这里插入图片描述

边际化：就是从P（A，B）中确认出P（B）（B 的概率相当于计算 A 的所有可能选择，并将所有选择的联合概率聚合在⼀起）

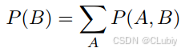
在这里插入图片描述

两个随机变量 A 和 B 是独⽴的，就是说事件 A 的发⽣不会透露有关 B 事件的发⽣情况的任何信息。通常将这⼀点描述为 A ⊥ B。根据⻉叶斯定理，就能得到 P(A | B) = P(A)。称之为两事件相互独立。由于 P(A | B) =(P（A，B）)/(P（B）) = P(A) 等价于 P(A，B) = P(A)P(B)，因此两个随机变量是独⽴的当且仅当两个随机变量的联合分布是其各⾃分布的乘积。
期望方差：（基本上都是一些公式，随便记一下就好了，知道是干嘛的就行）用来概括概率分布的关键特征的度量形式。
为了概括概率分布的关键特征，就需要⼀些测量⽅法（期望）。随机变量 X 的期望表⽰为：

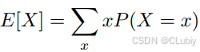
加入f（x）的输入是从P中抽取的随机变量时，f（x）的期望为：

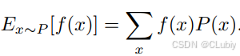
可以通过方差来量化随机变量x与其期望的偏置：

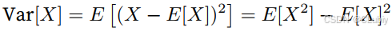
方差的平方根叫做标准差，随机变量函数的⽅差衡量的是，当从该随机变量分布中采样不同值 x 时，函数值偏离该函数的期望的程度：
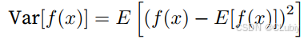
总结：
可以从概率分布中采样；
可以使⽤联合分布、条件分布、 Bayes 定理、边缘化和独⽴性假设来分析多个随机变量。