递归-二叉树中的深搜-2331.计算布尔二叉树的值-力扣(LeetCode)

个人主页:1白天的黑夜1-CSDN博客
专栏:力扣刷题录_1白天的黑夜1的博客-CSDN博客、企鹅程序员:Linux 系统与网络编程_1白天的黑夜1的博客-CSDN博客
目录
一、题目解析
1、非叶子节点要么值为2代表||,要么值为3代表&&
2、叶子节点要么值为1代表true,要么值为0代表false
3、该二叉树属于完全二叉树,即只有2个或0个孩子节点
4、计算根据非叶子节点代表的逻辑运算符对叶子节点进行逻辑运算
二、算法原理
解法:递归
角度1:以宏观看待递归
如何编写递归代码?
1、重复子问题-设计函数头
2、只关心某一个子问题做什么-函数体设计
3、递归函数出口
角度2:以后序遍历看待递归
递归代码编写
1、根据后序遍历递归调用,所以题目给的函数直接使用
2、先用一个bool类型的left接收递归函数左子树的返回值,再用一个right接收递归函数右子树的返回值
3、根据left和right以及root->val,计算逻辑值,如果root->val == 2,则返回left || right;如果root->val == 3,则返回left && right。
4、函数出口:当递归到叶子节点的时候们直接返回root->val即可,如果值为1,返回true,反之返回false
以角度1或角度2结合自己的思路,去尝试编写代码,提升自己的代码水平,题目链接如下
三、代码示例
四、递归展开图
看到最后,如果对您有所帮助,还请点赞、收藏和关注一键三连,在未来还会继续带来优秀的内容,感谢观看,我们下期再见!
一、题目解析
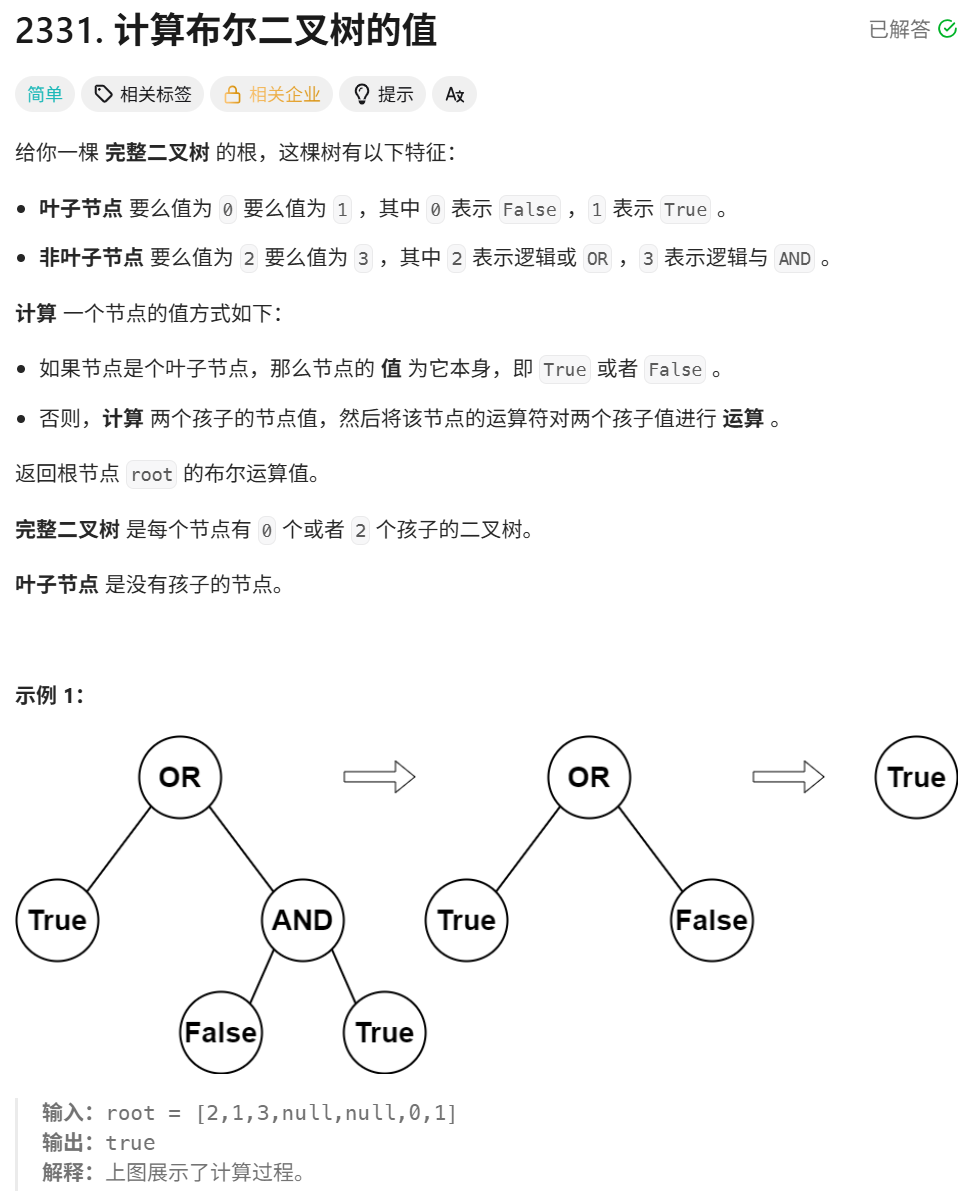
1、非叶子节点要么值为2代表||,要么值为3代表&&
2、叶子节点要么值为1代表true,要么值为0代表false
3、该二叉树属于完全二叉树,即只有2个或0个孩子节点
4、计算根据非叶子节点代表的逻辑运算符对叶子节点进行逻辑运算
二、算法原理
解法:递归
角度1:以宏观看待递归
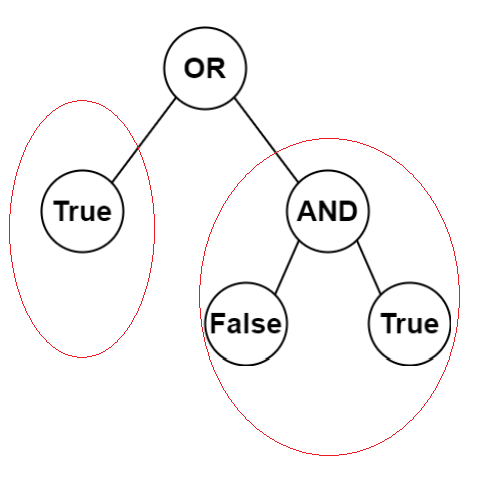
在计算它的逻辑值之前,我们得先知道它的左右两边的逻辑值,由此递推下去我们找到了重复子问题。
如何编写递归代码?
1、重复子问题-设计函数头
我们的重复子问题是计算子树的逻辑值,需要一个bool类型的返回值,还需要一个参数接收root的指针,所以可以直接用题目给出来的函数头。
2、只关心某一个子问题做什么-函数体设计
我们需要先遍历根的左树,然后遍历树的右树,根据返回值和根的逻辑运算符计算结果。
3、递归函数出口
如果一个递归函数没有函数出口,会导致递归层数过多,引发堆栈溢出,使程序报错。所以当访问到叶子节点的时候,直接返回叶子节点的val即可。
角度2:以后序遍历看待递归
根据计算过程在计算根的逻辑值时,需要先计算出左子树和右子树的逻辑值,这样的计算顺序不禁让我们联想到二叉树的后序遍历,即先左子树、右子树,后根的遍历方式。
递归代码编写
1、根据后序遍历递归调用,所以题目给的函数直接使用
2、先用一个bool类型的left接收递归函数左子树的返回值,再用一个right接收递归函数右子树的返回值
3、根据left和right以及root->val,计算逻辑值,如果root->val == 2,则返回left || right;如果root->val == 3,则返回left && right。
4、函数出口:当递归到叶子节点的时候们直接返回root->val即可,如果值为1,返回true,反之返回false
以角度1或角度2结合自己的思路,去尝试编写代码,提升自己的代码水平,题目链接如下
2331. 计算布尔二叉树的值 - 力扣(LeetCode)
三、代码示例
class Solution {
public:bool evaluateTree(TreeNode* root){if(root->left == nullptr && root->right == nullptr) return root->val;bool left = evaluateTree(root->left);bool right = evaluateTree(root->right);return root->val == 2 ? left || right : left && right; }
};
四、递归展开图
这里的递归展开图很简单,就是在而二叉树上模拟计算的过程
