当前位置：首页 > news >正文

数据结构（c++版）：二叉树的实现

news 2025/10/20 7:52:09

让我们走进"二叉树童话王国"，用生活中的故事理解每一个代码概念！

📚 第一章：书架的魔法格子——节点结构体

template<typename T>
struct treeNode
{T data;                // 格子里藏的宝物treeNode<T>* left;     // 左边的魔法门treeNode<T>* right;    // 右边的魔法门treeNode() :data(0), left(NULL), right(NULL) {};      // 空空的初始格子treeNode(T d) :data(d), left(NULL), right(NULL) {};   // 放入宝物的格子
};

🏰 城堡里的宝物格子

想象一座魔法城堡，每个房间都有一个特殊的宝物格子：

data：格子里藏的宝物（可能是金苹果、魔法书或水晶球）
left：左边的魔法门，通向比当前宝物"年龄小"的宝物房间
right：右边的魔法门，通向比当前宝物"年龄大"的宝物房间

🧙♂️ 老巫师的两种魔法：

treeNode()：创造一个空空的宝物格子（还没放入任何宝物）
treeNode(T d)：创造一个已经放入宝物d的格子

就像城堡管家说："第7号宝物格子放着'金苹果'，它左边的门通向3号房间，右边的门通向11号房间"

🏛️ 第二章：整个魔法城堡——二叉树类

template<typename T>
class Tree
{
private: treeNode<T>* nodes;    // 城堡所有房间的登记簿treeNode<T>* root;     // 城堡的主入口size_t nodesize;       // 城堡总房间数treeNode<T>* creat(T a[], int size, int nodeId, T nullNode);void visit(treeNode<T>* node);  // 参观一个宝物房间void preOrder(treeNode<T>* node);void inOrder(treeNode<T>* node);void postOrder(treeNode<T>* node);public:Tree();Tree(int maxidex);~Tree();treeNode<T>* Gertreenode(int Id);void creatTree(T a[], int size, T nullNode);void preorder();   // 探险路线1：先看当前，再看左右void inorder();    // 探险路线2：先看左，再看当前，最后右void postorder();  // 探险路线3：先看左右，最后看当前
};

🏯 魔法城堡的构造

nodes：城堡所有房间的登记簿（记录每个房间的位置和内容）
root：城堡的主入口大门（从这里开始探险）
nodesize：城堡总共有多少个房间

🗝️ 城堡的三种探险路线

preorder：勇者路线（先看当前宝物，再探索左右）
inorder：学者路线（按宝物年龄顺序探索）
postorder：清洁工路线（从最远的房间开始打扫）

🏗️ 第三章：建造与拆除城堡——构造与析构

// 默认建造能容纳100000个宝物的大城堡
template<typename T>
Tree<T>::Tree() { nodes = new treeNode<T>[100000]; }// 按国王的要求建造特定大小的城堡
template<typename T>
Tree<T>::Tree(int maxindex) { nodes = new treeNode<T>[maxindex]; }// 拆除城堡（当王国灭亡时）
template<typename T>
Tree<T>::~Tree() { delete[]nodes; }

👑 国王的建造令

默认城堡：当国王没说具体大小时，建一个能放100000个宝物的大城堡（Tree()）
定制城堡：当国王说"我要一个能放maxindex个宝物的城堡"（Tree(int maxindex)）
拆除城堡：当王国灭亡时，拆除整个城堡释放土地（~Tree()）

就像建筑大臣说："陛下，按您的要求，我们建造了一个有15个宝物房间的城堡！"

🗺️ 第四章：布置城堡房间——创建树

void Tree<T>::creatTree(T a[], int size, T nullNode) {root = creat(a, size, 1, nullNode); // 从1号主殿开始布置
}treeNode<T>* Tree<T>::creat(T a[], int size, int nodeId, T nullNode) {if (nodeId >= size || a[nodeId] == nullNode) {return NULL; // 这个位置不设宝物房间}treeNode<T>* nownode = Gertreenode(nodeId); // 找到这个房间nownode->data = a[nodeId]; // 放入宝物// 布置左边的房间（编号是当前的两倍）nownode->left = creat(a, size, 2 * nodeId, nullNode);// 布置右边的房间（编号是当前的两倍加一）nownode->right = creat(a, size, 2 * nodeId+1, nullNode);return nownode; // 返回布置好的房间
}

🧭 城堡布局规则

主殿：1号房间是城堡的主入口（root）
左翼：每个房间n的左房间是2n号
右翼：每个房间n的右房间是2n+1号
空房间：如果设计图上标记nullNode（如'-'），就不布置这个房间

🏗️ 布置过程：

拜访顺序：a → b → d → g → h → c → e → f → i

就像一位有礼貌的客人，每到一家都先问候最年长的主人，然后再去见他的孩子们。

第二把钥匙：🗝️ "年龄顺序"钥匙（中序遍历）

void inOrder(treeNode<T>* node) {if (node) {inOrder(node->left);  // 先拜访所有左边的晚辈visit(node);          // 然后问候当前长辈inOrder(node->right); // 最后拜访右边的晚辈}
}

拜访故事：
族长a说："这把钥匙的访客很讲究顺序，他们从最年轻的开始拜访，最后才来见我这位最年长的。"

拜访路线：

拜访顺序：g → d → h → b → a → e → c → i → f

就像整理家族相册，从最年轻的婴儿照片开始，慢慢看到最年长的祖辈照片。

第三把钥匙：🗝️ "晚辈优先"钥匙（后序遍历）

void postOrder(treeNode<T>* node) {if (node) {postOrder(node->left);  // 先拜访所有左边的晚辈postOrder(node->right); // 然后拜访右边的晚辈visit(node);            // 最后问候当前长辈}
}

拜访故事：
族长a笑着说："这把钥匙的访客最有耐心，他们要把所有孩子都见完了，最后才来见我这位老祖宗。"

拜访路线：

拜访顺序：g → h → d → b → e → i → f → c → a

就像发压岁钱，必须先给最小的孩子发完，最后才给最年长的长辈。

🌟 魔法钥匙的现实应用

🎄 圣诞节礼物配送（前序遍历）

圣诞老人用"族长优先"钥匙：

📚 图书馆整理书籍（中序遍历）

图书管理员用"年龄顺序"钥匙：

🧹 大扫除顺序（后序遍历）

清洁工用"晚辈优先"钥匙：

🎯 验证我们的魔法探险

int main() {const char nullNode = '-';char a[16] = {'-','a','b','c','d','-','e','f','g','h','-','-','i','-','-','-'};Tree<char> magicTree(16);magicTree.creatTree(a, 16, nullNode);cout << "族长优先钥匙: ";magicTree.preorder(); cout << endl;  // abdghceficout << "年龄顺序钥匙: ";magicTree.inorder(); cout << endl;   // gdhbaecifcout << "晚辈优先钥匙: ";magicTree.postorder(); cout << endl; // ghdbeifcareturn 0;
}

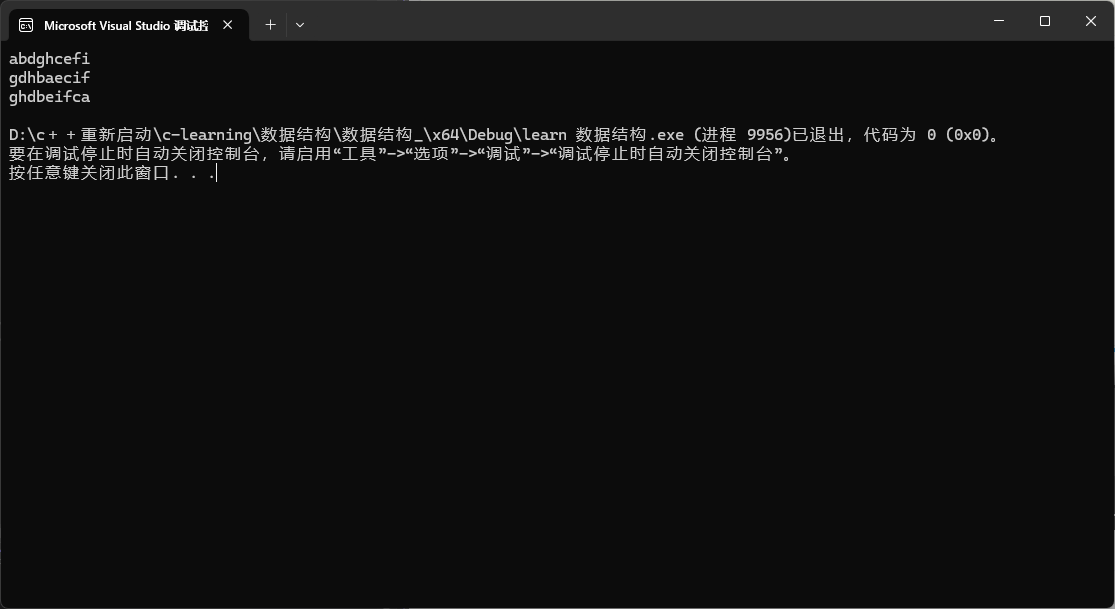
运行结果完全匹配我们的探险故事！ 🎉

💫 魔法森林的智慧

通过这次魔法森林的探险，我们学到了：

记住这个魔法口诀：

下次当你需要遍历一棵树时，就想想这座魔法森林，选择适合的钥匙来开启你的探险之旅！

管家拿着设计图(a[])走遍城堡
在1号主殿放入宝物'A'
然后去2号(1×2)左殿放宝物'B'
再去3号(1×2+1)右殿放宝物'C'
遇到'-'就跳过不布置

🌳 二叉树探险记：三把神奇钥匙打开魔法森林 🌳

想象一下，你面前有一座神秘的魔法森林，里面住着9个会说话的字魔法精灵：a、b、c、d、e、f、g、h、i。它们住在一棵神奇的家族树屋里，每个精灵都有自己的房间，房间之间用魔法楼梯相连。

🏰 魔法树屋的建造蓝图

char a[16] = {'-',   // 0号位置：地基，不建房'a',   // 1号：族长爷爷a的顶层套房'b',   // 2号：大儿子b的房间'c',   // 3号：二儿子c的房间  'd',   // 4号：孙子d的房间（b的孩子）'-',   // 5号：空房间（b的另一个孩子出国了）'e',   // 6号：孙子e的房间（c的孩子）'f',   // 7号：孙子f的房间（c的另一个孩子）'g',   // 8号：曾孙g的房间（d的孩子）'h',   // 9号：曾孙h的房间（d的另一个孩子）'-',   // 10号：空房间'-',   // 11号：空房间'i',   // 12号：曾孙i的房间（f的孩子）'-',   // 13号：空房间'-',   // 14号：空房间'-'    // 15号：空房间
};

        族长a（顶层）/      \儿子b     儿子c/        /   \孙子d    孙子e  孙子f/   \           /
曾孙g  曾孙h     曾孙i

🔑 三把神奇的拜访钥匙

森林守护者给了我们三把不同的魔法钥匙，每把钥匙都对应一种特殊的拜访顺序：

第一把钥匙：🗝️ "族长优先"钥匙（前序遍历）

void preOrder(treeNode<T>* node) {if(node) {visit(node);          // 先拜访当前房间的精灵preOrder(node->left);  // 然后探索左边的所有子孙preOrder(node->right); // 最后探索右边的所有子孙}
}

拜访故事：
族长爷爷a说："用这把钥匙的访客都很尊重长辈，他们总是先来拜访我！"

拜访路线：

🎯 先敲族长a的门："爷爷好！"
📍 然后去左边找儿子b："b叔叔好！"
📍 b说："先去见我左边的孩子d"
📍 d说："先见我左边的g"
👶 见到g："g小朋友好！"
📍 回到d："现在见我右边的h"
👶 见到h："h小朋友好！"
🔄 回到族长a："左边的都拜访完了，现在去右边"
📍 找儿子c："c叔叔好！"
📍 c说："先见我左边的e"
👶 见到e："e小朋友好！"
📍 c说："现在见我右边的f"
📍 f说："先见我左边的i"
👶 见到i："i小朋友好！"
🔍 从族长a开始，但先不敲门
📍 去找最左边的g（最小的曾孙）
👶 敲门："g小朋友好！"
↩️ 回到g的爸爸d："d叔叔好！"
📍 d说："现在去见我右边的h"
👶 见到h："h小朋友好！"
↩️ 回到d的爸爸b："b爷爷好！"
↩️ 回到族长a："族长爷爷好！"
📍 a说："现在去右边找e"
👶 见到e："e小朋友好！"
↩️ 回到e的爸爸c："c爷爷好！"
📍 c说："现在去见我右边的f"
📍 f说："先见我左边的i"
👶 见到i："i小朋友好！"
↩️ 回到f："f叔叔好！"
🔍 从族长a开始，但忍着不敲门
📍 先找到最左边的g
👶 敲门："g小朋友好！"
📍 然后找g的兄弟h
👶 敲门："h小朋友好！"
↩️ 回到g和h的爸爸d："d叔叔好！"
↩️ 回到d的爸爸b："b爷爷好！"
📍 现在去右边找e
👶 敲门："e小朋友好！"
📍 然后找f的孩子i
👶 敲门："i小朋友好！"
↩️ 回到i的爸爸f："f叔叔好！"
↩️ 回到f的爸爸c："c爷爷好！"
🎯 最后终于敲族长a的门："族长爷爷好！我们见过所有孩子了！"
先给族长送礼物，然后从左到右给孩子们送
确保最重要的长辈先收到礼物
从最旧的书开始整理，到最新的书
自然形成有序排列
从最里面的小房间开始打扫
最后打扫大厅，这样不会重复弄脏
不同的拜访顺序就像不同的社交礼仪
前序遍历尊重长辈，适合重要消息传递
中序遍历讲究顺序，适合整理和搜索
后序遍历关爱晚辈，适合清理和删除操作
前序：我在前，儿孙后
中序：儿在前，我在中，孙在后
后序：儿孙全拜访，最后见老子

(打扫主殿王冠）

🌟 第七章：二叉树王国的智慧

通过这个童话故事，我们学到了：

节点就像魔法房间：每个房间存放宝物，并有通向其他房间的门
建造规则：左房间编号是当前的2倍，右房间是2倍加1
三种探险方式：
- 勇者喜欢先看眼前（前序）
- 学者喜欢按顺序查看（中序）
- 清洁工从最底层开始（后序）

下次当你看到二叉树时，就想象这座魔法城堡，不同的遍历方式就像不同身份的人在城堡中探索！

源码及运行：

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<string>
#include<cstring>
using namespace std;
template<typename T>
struct treeNode
{T data;treeNode<T>* left;treeNode<T>* right;treeNode() :data(0), left(NULL), right(NULL) {};treeNode(T d) :data(d), left(NULL), right(NULL) {};};
template<typename T>class Tree
{
private: treeNode<T>* nodes;//所有节点的节点值相当于一个数组分配在堆上treeNode<T>* root;//根节点size_t nodesize;//有多少节点treeNode<T>* creat(T a[], int size, int nodeId, T nullNode);void visit(treeNode<T>* node);//访问单个节点时需要做些事情void preOrder(treeNode<T>* node);void inOrder(treeNode<T>* node);void postOrder(treeNode<T>* node);
public:Tree();Tree(int maxidex);~Tree();treeNode<T>* Gertreenode(int Id);void creatTree(T a[], int size, T nullNode);//传入一个顺序表储存的树从而生成二叉树, T nullNode要定义空树时用这个定义;void preorder();void inorder();void postorder();//因为给外部调用，从根节点开始所以不用传参
};
template<typename T>
Tree<T>::Tree()
{nodes = new treeNode<T>[100000];
}
template<typename T>
Tree<T>::Tree(int maxindex)
{nodesize = maxindex;nodes = new treeNode<T>[nodesize];
}
template<typename T>
Tree<T>::~Tree()
{delete[]nodes;}template<typename T>
treeNode<T>* Tree<T>::Gertreenode(int Id)
{return &nodes[Id];
}
template<typename T>
void Tree<T>:: creatTree(T a[], int size, T nullNode)
{root = creat(a, size, 1, nullNode);
}
template<typename T>
treeNode<T>* Tree<T>:: creat(T a[], int size, int nodeId, T nullNode)
{if (nodeId >= size || a[nodeId] == nullNode){return NULL;}treeNode<T>* nownode = Gertreenode(nodeId);nownode->data = a[nodeId];nownode->left = creat(a, size, 2 * nodeId, nullNode);nownode->right = creat(a, size, 2 * nodeId+1, nullNode);return nownode;
}
template<typename T>
void Tree<T>::visit(treeNode<T>* node)
{cout << node->data;
}
template<typename T>
void Tree<T>::preOrder(treeNode<T>* node)
{if(node){visit(node);preOrder(node->left);preOrder(node->right);}}
template<typename T>
void Tree<T>::inOrder(treeNode<T>* node)
{if (node){inOrder(node->left);visit(node);inOrder(node->right);}
}
template<typename T>
void Tree<T>::postOrder(treeNode<T>* node)
{if (node){postOrder(node->left);postOrder(node->right);visit(node);}
}
template<typename T>
void Tree<T>::preorder()
{preOrder(root);
}
template<typename T>
void Tree<T>::inorder()
{inOrder(root);
}
template<typename T>
void Tree<T>::postorder()
{postOrder(root);
}int main()
{const char nullNpde = '-';char a[15] ={nullNpde,'a','b','c','d',nullNpde,'e','f','g','h',nullNpde,nullNpde,nullNpde,nullNpde,'i'};Tree<char>T(15);T.creatTree(a, 15, nullNpde);T.preorder(); cout << endl;T.inorder(); cout << endl;T.postorder(); cout << endl;return 0;}