利用汽车雷达测试系统模拟多径效应——论文阅读
利用汽车雷达测试系统模拟多径效应
引言:汽车雷达面临的现实挑战
在现代汽车技术中,尤其是高级驾驶辅助系统(ADAS)和自动驾驶领域,雷达传感器扮演着至关重要的角色。它们通过发射射频信号并处理返回的回波来感知周围的交通环境,从而实现目标探测、跟踪、测距和测速等核心功能。雷达目标的关键参数包括距离、速度、雷达截面积(RCS)以及到达角(AoA)。
传统上,对这些雷达传感器的测试方法主要有两种:一是进行大规模的道路测试,二是在实验室等受控环境中使用已知的目标(如角反射器或雷达目标模拟器)进行测试。然而,这两种方法都存在局限性。道路测试成本高、周期长且难以复现特定的危险场景;而传统的实验室测试通常将目标模拟为孤立的点,忽略了真实驾驶环境中一个普遍且棘手的问题——多径传播。
汽车雷达通常安装在离地面较低的位置,这意味着雷达波束会以很小的掠射角照射到路面。路面并非理想的吸收体,它会像镜子一样反射雷达信号,产生相干的镜面反射。这导致除了雷达与目标之间的直接传播路径外,还存在至少一条经由地面反射的间接路径。在复杂场景中,还可能存在来自护栏、隧道墙壁或其他车辆的水平反射。这些额外的反射路径不仅会产生杂波,还可能导致雷达误判,在没有真实物体的地方识别出所谓的“鬼影目标”,对驾驶安全构成严重威胁。
因此,本文的核心目标,就是提出一种新颖的方法,利用先进的雷达目标模拟器(RTS)在实验室环境中精确地复现和模拟这种由地面反射引起的多径效应,从而能够更全面、更真实地评估雷达传感器在复杂环境下的性能。
核心概念与数学建模
为了理解并模拟多径效应,论文首先建立了一个简化的二维几何模型,该模型捕捉了垂直平面内多径传播的关键物理过程。
多径传播的几何模型
该模型考虑了两个关键实体:一个是安装在离地高度为 hrh_rhr 的雷达传感器,它正以速度 vrv_rvr 向前移动;另一个是位于前方距离 ddd 处、高度为 hth_tht 的静止目标。在这种情况下,雷达信号的传播主要存在两条路径:
- 直接路径 (Direct Path) :信号从雷达直接传播到目标,然后直接返回雷达。
- 间接路径 (Indirect Path) :信号从雷达发出,经地面反射一次后到达目标,再由目标反射回来(同样可能经历直接返回或间接返回)。
下图直观地展示了这个几何模型。
图 1:水平表面上多径传播的简化几何模型
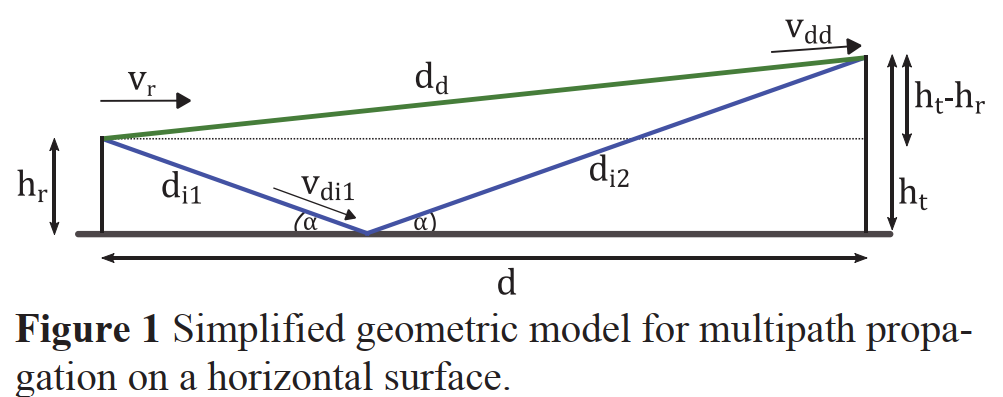
这张图是一个侧视图,描绘了多径传播的几何关系。左侧是雷达传感器,位于高度 hrh_rhr 处,并带有一个表示其运动速度 vrv_rvr 的箭头。右侧是目标,位于高度 hth_tht。两者之间的水平距离为 ddd。图中用一条实线连接传感器和目标,代表了信号的直接传播路径,其单程长度为 ddd_ddd。由于雷达在运动,沿这条路径会产生一个径向速度分量 vddv_{dd}vdd。图中还用两条虚线表示了间接传播路径,信号从传感器发出,在地面上某一点发生镜面反射,然后到达目标。这条路径的总长度由两部分组成:di1d_{i1}di1(从传感器到反射点)和 di2d_{i2}di2(从反射点到目标)。这条间接路径同样会因为雷达的运动而引入多普勒频移,在传感器处报告的速度为 vdi1v_{di1}vdi1。
基于这个模型,一个完整的雷达发射-接收过程实际上包含了四种可能的传播组合,每一种组合都有其独特的总路径长度和有效速度,如下表所示。
| 传播路径 | 路径长度 dnd_ndn | 有效速度 |
|---|---|---|
| 直接-直接 (direct-direct) | 2dd2d_d2dd | 2vdd2v_{dd}2vdd |
| 间接-间接 (indirect-indirect) | 2(di1+di2)2(d_{i1} + d_{i2})2(di1+di2) | 2vdi12v_{di1}2vdi1 |
| 直接-间接 (direct-indirect) | dd+di1+di2d_d + d_{i1} + d_{i2}dd+di1+di2 | vdd+vdi1v_{dd} + v_{di1}vdd+vdi1 |
| 间接-直接 (indirect-direct) | dd+di1+di2d_d + d_{i1} + d_{i2}dd+di1+di2 | vdd+vdi1v_{dd} + v_{di1}vdd+vdi1 |
(表1: 所有反射路径的长度和速度)
除了代表真实目标的“直接-直接”路径外,其他三条路径都是由多径效应产生的“鬼影”。对于那些距离和高程分辨率有限的雷达系统(尤其是长距离雷达),它们无法将这四条路径长度非常接近的信号区分开来。结果就是,雷达接收机实际处理的是这四路信号的矢量叠加。由于各路径长度不同,信号到达接收机时的相位也不同,这将导致信号之间发生相长或相消干涉。当车辆驶向目标时,距离 ddd 不断变化,路径长度差也随之改变,最终导致雷达接收到的信号功率呈现出周期性的振荡。
软件仿真与干涉图样
为了从理论上验证这种干涉现象,研究人员首先进行了软件仿真。对于广泛应用于汽车雷达的调频连续波(FMCW)雷达而言,其接收信号在经过下变频处理后,可以被表示为四路正弦波形(复数形式)的叠加:
Cr=∣∑n=14An(cos(ωnt+φn)+jsin(ωnt+φn))∣C_{r}=|\sum_{n=1}^{4}A_{n}(\cos(\omega_{n}t+\varphi_{n})+j\sin(\omega_{n}t+\varphi_{n}))|Cr=∣n=1∑4An(cos(ωnt+φn)+jsin(ωnt+φn))∣
在这个公式中,AnA_nAn 代表第 nnn 条路径的回波幅度,ωn\omega_nωn 是其对应的差拍频率,而关键的相位项 φn\varphi_nφn 则由路径长度决定:
φn=2πλdn\varphi_{n} = \frac{2\pi}{\lambda} d_nφn=λ2πdn
其中 λ\lambdaλ 是雷达工作波长(仿真中取值为3.12毫米,对应约77GHz频段)。信号的干涉(相长或相消)完全取决于这四路信号的相位差 Δφ\Delta\varphiΔφ。
在仿真中,研究人员做了一些理想化假设,例如所有路径的回波幅度都相等(An=1A_n=1An=1),即地面为理想的无损反射面,并且雷达自身是静止的(vr=0v_r=0vr=0)。然后,通过在程序中不断改变目标距离 ddd 和目标高度 hth_tht(雷达高度固定为 hr=0.3h_r=0.3hr=0.3 米),计算出合成信号的总幅度 CrC_rCr。仿真结果被绘制成一幅二维彩色图。
图 2:仿真信号幅度 C r C_r Cr 随目标距离 d d d 和高度 h t h_t ht 的变化
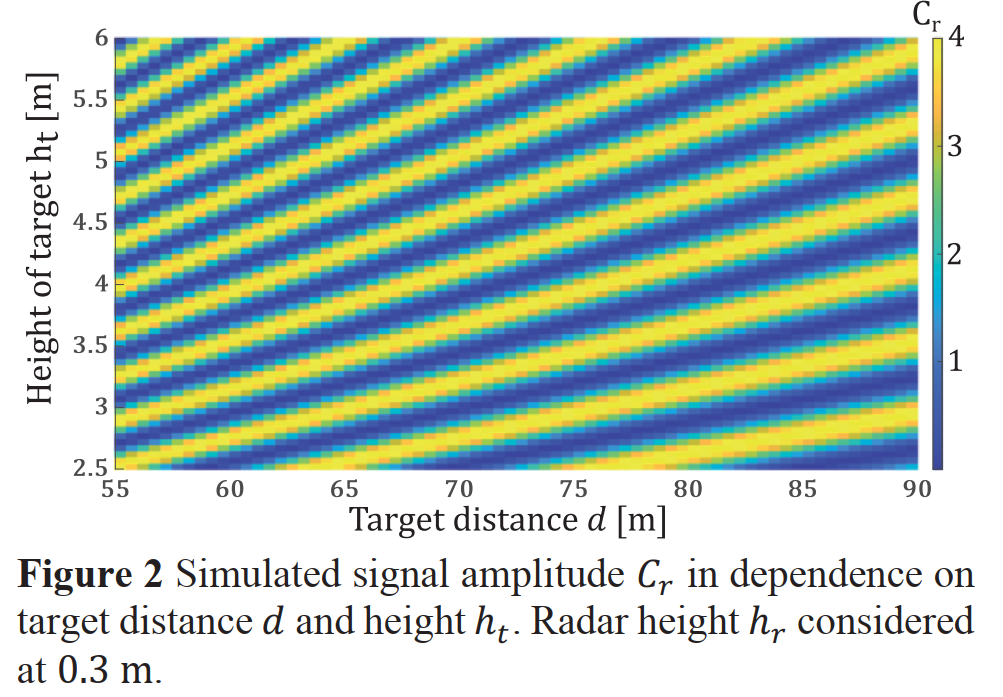
这张图展示了纯软件仿真的结果。它的横轴是目标距离 ddd,范围从55米到90米;纵轴是目标高度 hth_tht,范围从2.5米到6米。图中的颜色深浅代表了合成信号幅度 CrC_rCr 的大小,从0(完全相消,深蓝色)到4(四路信号完全同相叠加,亮黄色)。最引人注目的是图中呈现出非常清晰、规律的斜向条纹图案。这些条纹就是干涉条纹。每一条亮黄色条纹代表了在该距离和高度组合下,四路信号发生了强烈的相长干涉;而深蓝色条纹则代表发生了相消干涉。条纹的倾斜和密度变化,直观地展示了多径干涉效应对雷达回波强度的复杂影响。
实验验证与结果分析
理论仿真的结果很好,但更重要的是能否在现实中通过硬件设备复现这一现象。为此,研究团队搭建了一个精密的测量平台。
测量设置
实验的核心设备是是德科技(Keysight)的AD1012A雷达场景模拟器(RTS),它由多个可独立编程和相位同步的小型化雷达目标模拟器(mRTS)单元组成。而被测设备(DUT)则是一块德州仪器(TI)的AWR1642雷达评估板,它被设置为长距离探测模式,这意味着其距离分辨率相对有限(0.38米),这恰好符合之前提到的易受多径效应影响的雷达类型。
实验设置如下图所示。
图 3:测量设置示意图
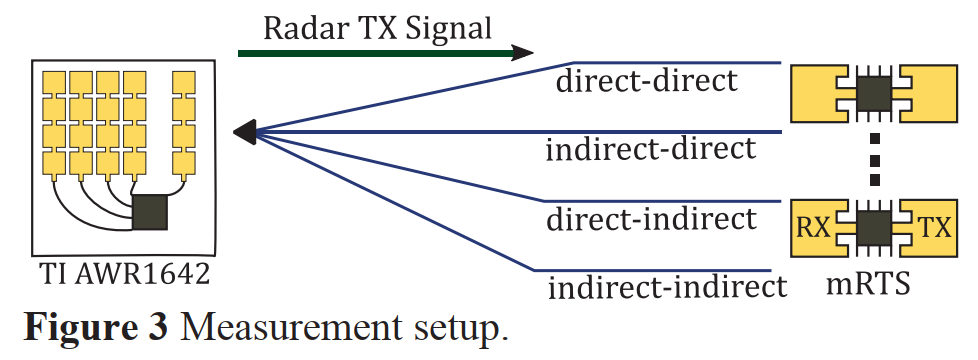
此图描绘了实验装置的布局。AWR1642雷达作为发射源(TX)和接收机(RX)。在距离雷达约0.8米的位置,阵列式地放置了多个mRTS单元。这些mRTS单元接收到雷达发射的信号后,并不会像真实目标那样直接反射,而是会根据预设的程序,对信号进行精确的延迟、多普勒频移和相位调整,然后再将信号发射回雷达的接收机。通过为四个mRTS单元分别编程,使其精确模拟前述理论模型中的四条传播路径(直接-直接、间接-间接、直接-间接、间接-直接)的参数,从而在硬件层面上“合成”出一个带有完整多径效应的虚拟目标。
在实验中,研究人员模拟了雷达以 vr=2.78v_r = 2.78vr=2.78 m/s 的恒定速度行驶的场景。虽然理论上不同路径的掠射角不同,会导致微小的多普勒频移差异(由公式3和4描述),但计算表明,这些差异远小于AWR1642雷达0.09 m/s的速度分辨率。因此,在本次实验中,可以合理地假设所有路径的多普勒频移近似相等。实验过程就是,通过程序控制mRTS,不断改变模拟的目标距离 ddd 和高度 hth_tht,并记录雷达接收到的信号幅度。
结果与分析
经过大量的测量,实验数据被汇集成与仿真图类似的二维彩色图。
图 4:测量的信号幅度 C r C_r Cr 随目标距离 d d d 和高度 h t h_t ht 的变化
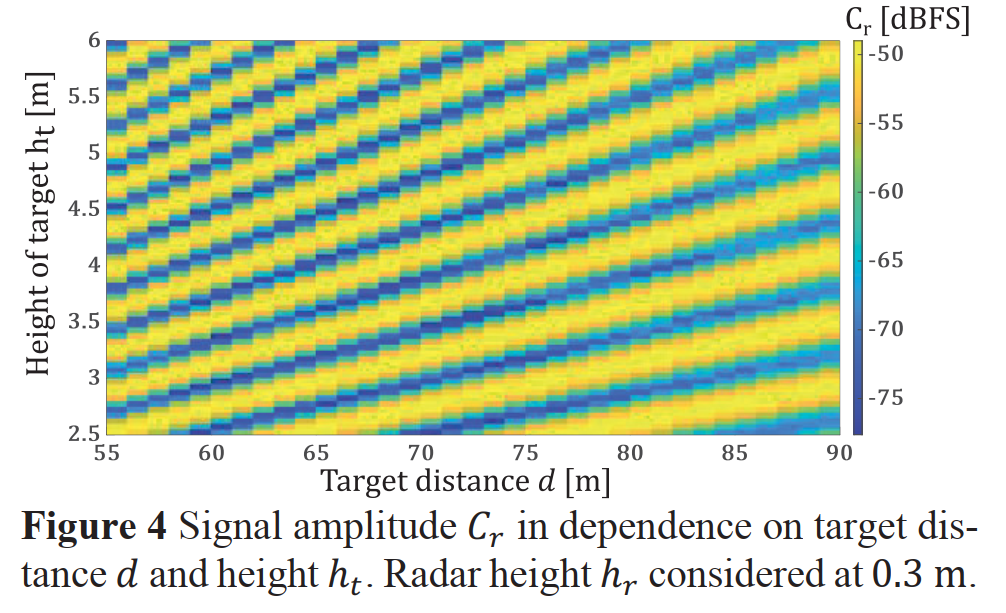
这张图是本次实验的核心成果,是图2的真实硬件测量版本。其坐标轴与图2完全对应。颜色代表雷达实际测量到的信号强度,单位为dBFS(相对于满量程的分贝数)。我们可以清晰地看到,图中同样呈现出与软件仿真结果高度相似的斜向干涉条纹。信号强度的最大值和最小值之间差异可达25dB,形成了明显的波峰和波谷。这也验证了之前的理论预测:随着目标高度的增加,干涉条纹变得更密集,意味着信号强度随距离变化的振荡频率加快。这张图有力地证明了使用RTS系统来模拟多径效应是完全可行的。
为了更定量地比较仿真与测量的吻合程度,研究人员选取了目标高度 ht=4.5h_t=4.5ht=4.5 米这一个特定的切片,将仿真曲线和测量曲线绘制在同一张图上。
图 5:在 h t = 4.5 h_t=4.5 ht=4.5 m 时,测量与仿真的信号幅度 C r C_r Cr 对比
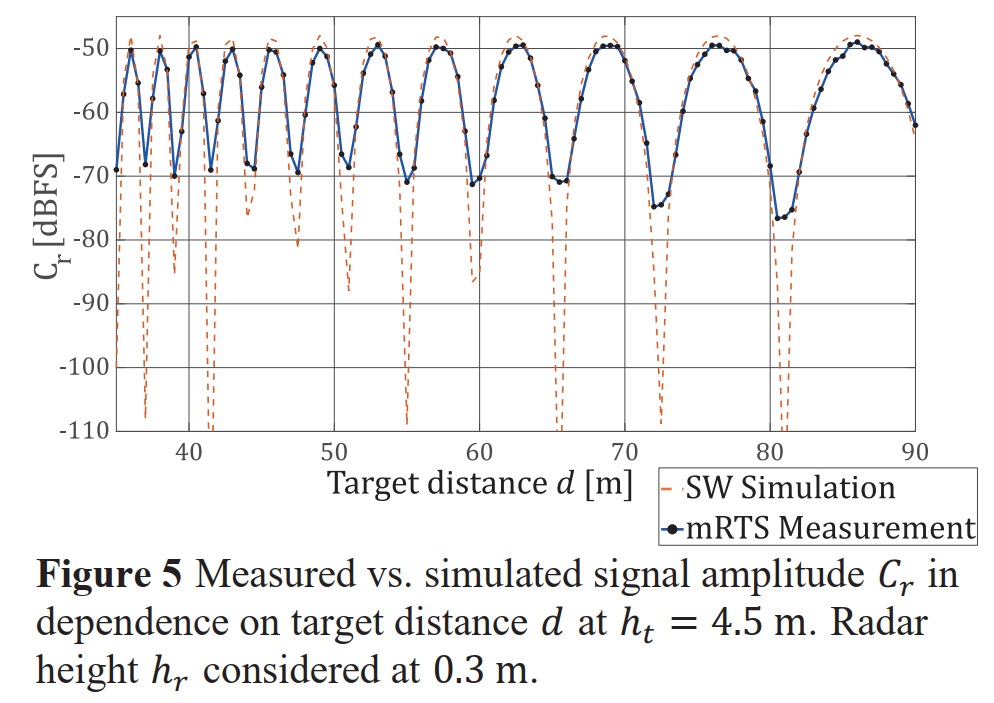
这张线图的横轴是目标距离 ddd,纵轴是信号幅度 CrC_rCr(单位dBFS)。图中包含两条曲线:一条是经过调整的软件仿真结果(SW Simulation),另一条是mRTS的实际测量数据(mRTS Measurement)。为了便于比较,仿真的线性幅度被转换成了对数刻度,并且应用了一个简化的自由空间路径损耗模型。从图中可以非常直观地看到,两条曲线的振荡模式——即波峰和波谷出现的位置——吻合得非常好,这表明所建立的几何模型和相位关系是准确的。
当然,两条曲线也存在一些差异。最明显的是,仿真曲线的“波谷”比测量曲线的要深得多。这是因为仿真基于理想假设,即地面是完美反射体,信号可以完全相消(幅度为0,即-∞ dBFS)。而在实际测量中,mRTS自身的系统噪声、实验环境中的杂散反射以及各单元之间微小的相位未对准等因素,都会使得信号无法完全抵消,因此波谷不会那么深。尽管存在这些差异,但总体特征的高度一致性已经足以证明该方法的成功。
结论与未来展望
本文成功地提出并验证了一种利用多个相位同步的雷达目标模拟器来模拟地面反射多径效应的概念。通过将一个简化的数学模型编程输入到是德科技的雷达场景模拟器中,实验成功地在硬件上复现了由多径干涉引起的特征性信号幅度振荡图样,且测量结果与软件仿真高度吻合。
这标志着一个重要的进步,它被视为一个“概念验证”,为未来更复杂的汽车雷达场景模拟铺平了道路。目前的研究采用了等权重的理想反射模型,未来的工作将致力于提升模型的真实性,主要包括以下几个方面:
- 引入更真实的反射系数:现实中地面的反射强度与雷达波的入射角、极化方式以及路面材质(沥青、混凝土、湿滑路面等)密切相关。未来模型将引入这些因素。
- 考虑路径损耗与散射:不同路径的长度不同,其自由空间损耗也应不同。此外,除了镜面反射,还应考虑粗糙路面引起的漫散射效应。
- 扩展到更复杂的场景:模型将扩展到包含水平方向的多径效应,例如来自护栏、隧道墙壁、建筑物或其他车辆的反射。同时,也会考虑来自车辆底部等特殊结构的反射。
附录:关键数学公式推导
本文原文中省略了具体的几何推导过程,但我们可以基于其提供的图1轻松推导出关键的路径长度公式。
1. 直接路径长度 d d d_d dd 的推导
观察图1,雷达传感器、目标以及从传感器位置引出的水平线构成了一个直角三角形。
- 该直角三角形的一条直角边是雷达与目标的水平距离 ddd。
- 另一条直角边是目标与雷达的高度差,即 (ht−hr)(h_t - h_r)(ht−hr)。
- 直接路径 ddd_ddd 是这个直角三角形的斜边。
根据勾股定理,我们可以得到:
dd2=d2+(ht−hr)2d_d^2 = d^2 + (h_t - h_r)^2dd2=d2+(ht−hr)2
因此,直接路径的单程长度为:
dd=d2+(ht−hr)2d_d = \sqrt{d^2 + (h_t - h_r)^2}dd=d2+(ht−hr)2
2. 间接路径总长度 d i = d i 1 + d i 2 d_i = d_{i1} + d_{i2} di=di1+di2 的推导
对于地面反射,我们可以使用“镜像法”来简化计算。将地面视为一面镜子,我们可以找到雷达传感器在地面下的一个“镜像点”,其位于地面下方 hrh_rhr 处。
- 从这个镜像点到真实目标的直线路径,其长度根据几何光学原理,就等于间接路径的总长度 di1+di2d_{i1} + d_{i2}di1+di2。
- 我们现在可以构建一个新的直角三角形。其一条直角边仍然是水平距离 ddd。
- 另一条直角边则是目标高度与雷达镜像点深度之和,即 (ht+hr)(h_t + h_r)(ht+hr)。
- 间接路径的总长度 did_idi 就是这个新直角三角形的斜边。
同样根据勾股定理:
di2=d2+(ht+hr)2d_i^2 = d^2 + (h_t + h_r)^2di2=d2+(ht+hr)2
因此,间接路径的单程总长度为:
di=di1+di2=d2+(ht+hr)2d_i = d_{i1} + d_{i2} = \sqrt{d^2 + (h_t + h_r)^2}di=di1+di2=d2+(ht+hr)2
3. 路径长度差 Δ d \Delta d Δd
多径干涉的核心在于不同路径之间的长度差,因为它直接决定了相位差。单程的直接路径与间接路径的长度差为:
Δd=di−dd=d2+(ht+hr)2−d2+(ht−hr)2\Delta d = d_i - d_d = \sqrt{d^2 + (h_t + h_r)^2} - \sqrt{d^2 + (h_t - h_r)^2}Δd=di−dd=d2+(ht+hr)2−d2+(ht−hr)2
这个 Δd\Delta dΔd 的值随着距离 ddd 的变化而变化,导致了相位差的改变,从而产生了我们在图2和图4中看到的周期性振荡的干涉条纹。
