动态规划的“降维”艺术:二维矩阵中的建筑奇迹——最大矩形
哈喽,各位,我是前端小L。
我们的DP之旅,已经探索了序列、树、乃至各种抽象的匹配和计数问题。今天,我们重返二维矩阵这片熟悉的土地,但要挑战一个全新的、更具“几何感”的目标:在这片由0和1构成的土地上,圈出那块只包含1的、面积最大的矩形地块。
这道题是DP与数据结构(特别是单调栈)结合的典范。它将向我们展示,最高级的算法思想,往往不是硬碰硬地增加维度,而是巧妙地**“降维打击”**,将一个高维度的难题,分解成我们能够轻松解决的低维度问题。
力扣 85. 最大矩形
https://leetcode.cn/problems/maximal-rectangle/
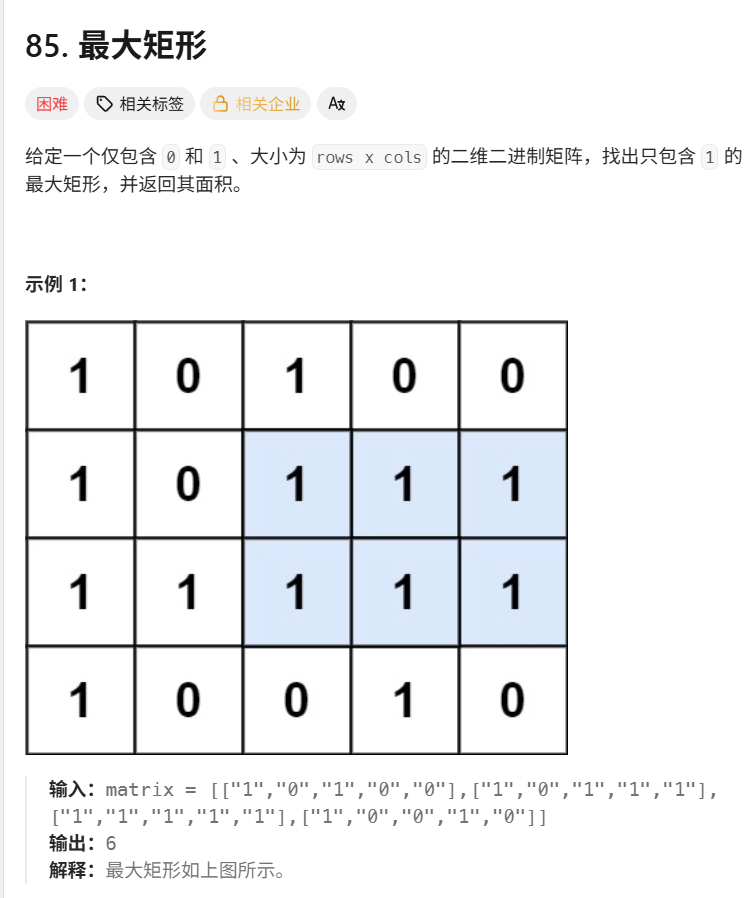
题目分析: 在一个由 0 和 1 组成的二维矩阵中,找到只包含 1 的最大矩形的面积。
思路一:朴素DP的尝试与瓶颈
一个很自然的想法是,我们能否用 dp[i][j] 来记录一些信息,从而推导出答案? 我们可以定义 dp[i][j] 为:在以 (i, j) 为右下角的矩形中,只包含1的最大面积。 但这很难!因为要确定面积,dp[i][j] 不仅需要知道自己的高度和宽度,还需要知道 dp[i-1][j], dp[i][j-1] 等多个状态的几何信息,状态转移会变得异常复杂。
一个稍微好一点的定义是:dp[i][j] 表示在第 i 行,以 (i, j) 结尾的连续 1 的个数(即宽度)。 dp[i][j] = (matrix[i][j] == '1') ? dp[i][j-1] + 1 : 0 有了这个“宽度”信息后,要计算以 (i, j) 为右下角的矩形的最大面积,我们还需要向上遍历 k 从 i 到 0,找出在这些行中,[k...i] 范围内宽度的最小值,然后乘以高度 (i-k+1)。 这个思路的时间复杂度是 O(m * n * m),依然不够理想。
思路二:“Aha!”时刻 —— 从矩阵到直方图的降维打击
让我们换一个视角,逐行地审视这个矩阵。 当我们处理到第 i 行时,我们不把它看作孤立的一行,而是把它看作一个**“地基”**。
我们可以定义一个 heights 数组,heights[j] 表示在第 i 行、第 j 列的位置,向上能延伸的连续 1 的最大高度。
举个例子: matrix = [ ["1","0","1","0","0"], ["1","0","1","1","1"], <-- 我们现在处理到这一行 (i=1) ["1","1","1","1","1"], ["1","0","0","1","0"] ]
当 i = 1 时,我们来计算每个位置的“高度”:
-
heights[0]:matrix[0][0]和matrix[1][0]都是1,所以高度是2。 -
heights[1]:matrix[1][1]是0,高度中断,所以是0。 -
heights[2]:matrix[0][2]和matrix[1][2]都是1,所以高度是2。 -
heights[3]:matrix[0][3]是0,matrix[1][3]是1,所以高度是1。 -
heights[4]:matrix[0][4]是0,matrix[1][4]是1,所以高度是1。
在第 i=1 行,我们得到了一个高度数组:heights = [2, 0, 2, 1, 1]。
现在,最关键的一步来了! 在以第 i 行为“地基”的所有可能矩形中,寻找面积最大的那个,这个问题,与在一个由 heights 数组构成的“直方图”中,寻找最大矩形面积的问题,是完全等价的!
这不就是我们另一道经典难题 LC 84. 柱状图中最大的矩形 吗?!
我们成功地,把一个二维的 (m*n) 矩阵问题,分解成了 m 个一维的 (1*n) 直方图问题!
最终算法:逐行构建直方图 + 单调栈
现在,我们的宏伟蓝图已经清晰了:
-
初始化
maxArea = 0。 -
创建一个
heights数组,长度为n(矩阵的列数),初始为0。 -
逐行遍历矩阵 (从
i = 0到m-1): a. 更新heights数组:遍历当前行i的每一列j。 * 如果matrix[i][j] == '1',那么heights[j]的高度就增加1。 * 如果matrix[i][j] == '0',说明连续的1在此中断,heights[j]的高度必须归零。 b. 解决子问题:对当前更新后的heights数组,调用“柱状图中最大的矩形”的解法(通常使用单调栈),计算出当前行的最大矩形面积currentMax。 c. 更新全局最优解:maxArea = max(maxArea, currentMax)。 -
所有行遍历完毕后,
maxArea就是最终答案。
代码实现 (融合 LC 84 的解法)
#include <stack>
class Solution {
public:int maximalRectangle(vector<vector<char>>& matrix) {if (matrix.empty() || matrix[0].empty()) {return 0;}int m = matrix.size();int n = matrix[0].size();vector<int> heights(n, 0);int maxArea = 0;for (int i = 0; i < m; ++i) {// 1. 更新 heights 数组for (int j = 0; j < n; ++j) {if (matrix[i][j] == '1') {heights[j] += 1;} else {heights[j] = 0;}}// 2. 调用 LC 84 的解法maxArea = max(maxArea, largestRectangleInHistogram(heights));}return maxArea;}private:// LeetCode 84: 柱状图中最大的矩形 (单调栈解法)int largestRectangleInHistogram(vector<int>& heights) {stack<int> s;heights.push_back(0); // 哨兵,确保所有柱子都能被弹出计算int maxArea = 0;for (int i = 0; i < heights.size(); ++i) {while (!s.empty() && heights[s.top()] >= heights[i]) {int h = heights[s.top()];s.pop();int w = s.empty() ? i : i - s.top() - 1;maxArea = max(maxArea, h * w);}s.push(i);}heights.pop_back(); // 恢复原状 (好习惯)return maxArea;}
};总结:DP思维的更高境界
今天这道题,是动态规划思想的一次华丽“变身”。它深刻地告诉我们:
最高级的DP,有时并不是构建更复杂的DP状态,而是将原问题分解、转化为我们已知的、更简单的DP模型。
这种**“问题转化”或“降维”**的能力,是衡量一个算法工程师水平高低的重要标志。它要求我们不仅要会“做题”,更要在大脑中建立起一个“问题模型库”,在面对新问题时,能够迅速地进行模式匹配。
从今天起,当你再遇到一个看似棘手的二维矩阵问题时,不妨问问自己:“我能不能把它切成一片片,变成我熟悉的一维问题来解决?”
咱们下期见~
