【算法与数据结构】拓扑排序实战（栈+邻接表+环判断，附可运行代码）

拓扑排序实战！教材P301图8.43手把手通关（栈+邻接表+环判断，附可运行代码）

刚做拓扑排序实验时，我对着屏幕卡了俩小时：一是教材P301图8.43的7个顶点关系理不清，不知道“1→3”“2→7”这些边怎么对应代码；二是跑原文代码时，因为少写个逗号（n m写成nm）编译报错，还没加环判断，明明图没问题却输出不全。后来才发现，拓扑排序的核心就像“选课”——先选无先修课的（入度0），选完解锁后续课（入度减1），用栈存“能选的课”就行。

今天就把这份能直接跑通的教程拆透，从教材图的结构可视化，到代码逐行注释，再到一步步走流程，新手也能复现“1 2 3 4 5 7 6”的正确序列，还会指出实验必踩的坑。

一、先看懂：实验用的图长啥样？（教材P301图8.43）

实验的核心是7个顶点（编号1-7）、8条边的有向图，可以理解为“简化选课系统”：顶点是课程，有向边i→j表示“选j课前必须先选i”。先把边和入度（先修课数量）列清楚，后续所有操作都围绕它展开：

有向边	选课逻辑（j的先修课是i）	顶点初始入度（先修课数量）
1→3	选3课前先选1	1：0；3：1
2→4、2→5、2→7	选4/5/7前先选2	2：0；4：2；5：2；7：1
3→4	选4前也能先选3	4：2（先修2和3）
4→5、4→6	选5/6前先选4	5：2（先修2和4）；6：2
7→6	选6前先选7	6：2（先修4和7）

简单说：入度为0的顶点（1、2）是“无先修课的课”，能优先选；选完后减少后续课程的入度，入度变0就能继续选。

二、核心原理：3句话讲透拓扑排序

不用记复杂定义，用大白话理解核心：

1. 拓扑序列：比如“1 2 3 4 5 7 6”，所有边i→j都满足“i在j前面”（先选i，再选j），符合选课逻辑；
2. 入度：顶点的“先修课数量”，入度=0 → 无先修，能优先处理；
3. 算法逻辑：用栈存“入度0的顶点”（能选的课），处理后解锁后续顶点（入度-1），重复到所有顶点输出（无环）或栈空（有环）。

三、完整可运行代码

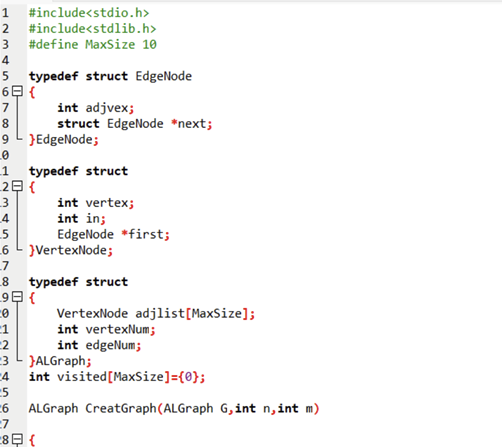
#include<stdio.h>
#include<stdlib.h>
#define MaxSize 10  // 足够存7个顶点// 1. 边节点（邻接表的“边”：存邻接顶点+下一条边）
typedef struct EdgeNode {int adjvex;          // 邻接顶点编号（比如1的邻接顶点是3）struct EdgeNode *next; // 下一条边的指针
} EdgeNode;// 2. 顶点节点（邻接表的“顶点”：存编号+入度+第一条边）
typedef struct VertexNode {int vertex;          // 顶点编号（1-7）int in;              // 入度（先修课数量）EdgeNode *first;     // 指向第一条边的指针
} VertexNode;// 3. 图结构（邻接表）
typedef struct {VertexNode adjlist[MaxSize];  // 所有顶点的数组int vertexNum;                // 顶点总数（实验中7）int edgeNum;                  // 边总数（实验中8）
} ALGraph;// 4. 创建图：用头插法建邻接表（输入边的关系）
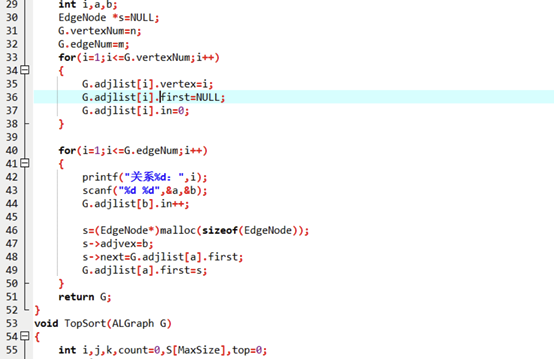
ALGraph CreatGraph(ALGraph G, int n, int m) {int i, a, b;          // a→b：有向边EdgeNode *s = NULL;   // 临时边节点G.vertexNum = n;      // 赋值顶点数G.edgeNum = m;        // 赋值边数// 初始化每个顶点：编号、入度0、无第一条边for (i = 1; i <= G.vertexNum; i++) {G.adjlist[i].vertex = i;G.adjlist[i].in = 0;G.adjlist[i].first = NULL;}// 输入每条边，头插法插入邻接表for (i = 1; i <= G.edgeNum; i++) {printf("第%d条边（a→b）：", i);scanf("%d %d", &a, &b);// ① 更新b的入度（b多一个先修课a）G.adjlist[b].in++;// ② 创建边节点，插入a的邻接表（头插法：新边在最前面）s = (EdgeNode*)malloc(sizeof(EdgeNode));s->adjvex = b;          // 边指向bs->next = G.adjlist[a].first;  // 新边接在原有边前面G.adjlist[a].first = s;       // a的第一条边指向新边}return G;
}// 5. 核心：栈实现拓扑排序（含环判断）
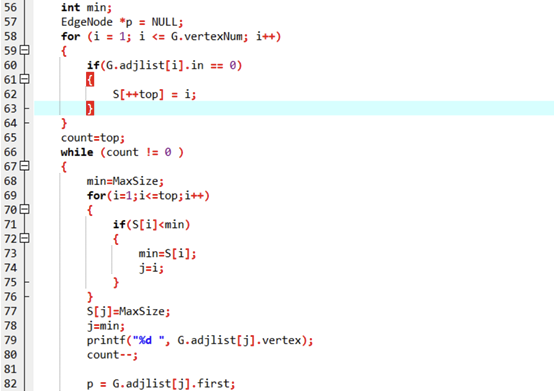
void TopSort(ALGraph G) {int i, j, k, count = 0;  // count：已输出的顶点数int S[MaxSize], top = 0; // 栈S：存放入度0的顶点，top=栈顶指针EdgeNode *p = NULL;      // 遍历边的指针// 第一步：初始化栈：入度0的顶点压栈（能先选的课）for (i = 1; i <= G.vertexNum; i++) {if (G.adjlist[i].in == 0) {S[++top] = i;  // 栈从1开始存（top初始0，++top后是1）}}// 第二步：处理栈中顶点，直到栈空while (top != 0) {// ① 弹出栈顶顶点（选当前能选的课）j = S[top--];printf("%d ", G.adjlist[j].vertex);  // 输出顶点count++;                              // 已输出数+1// ② 处理该顶点的所有邻接边（解锁后续课）p = G.adjlist[j].first;  // 取j的第一条边while (p != NULL) {k = p->adjvex;       // 邻接顶点k（j→k）G.adjlist[k].in--;   // k的入度-1（少一个先修课）// ③ 若k的入度变0（先修课全满足），压栈if (G.adjlist[k].in == 0) {S[++top] = k;}p = p->next;  // 遍历下一条边}}// 第三步：判断是否有环（输出数<总顶点数→有环）if (count < G.vertexNum) {printf("\n⚠️  有向图存在环，无法拓扑排序！");}
}// 主函数：测试教材P301图8.43（7顶点8边）
int main() {ALGraph G;int n = 7, m = 8;  // 实验图参数：7个顶点，8条边// 1. 创建图（输入教材图的8条边：1 3;2 4;2 5;2 7;3 4;4 5;4 6;7 6）printf("=== 教材P301图8.43（7顶点8边）===\n");G = CreatGraph(G, n, m);  // 修正原文：n和m之间加逗号// 2. 拓扑排序printf("\n拓扑排序结果：");TopSort(G);return 0;
}

四、流程拆解：用教材例子一步步走（新手必看）

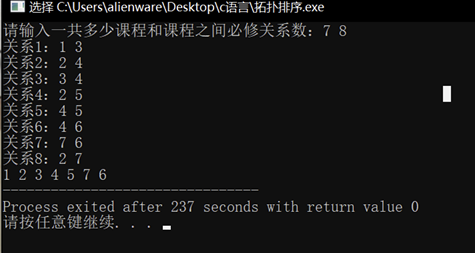
以教材图8.43为例，输入边为1 3;2 4;2 5;2 7;3 4;4 5;4 6;7 6，一步步看栈和入度的变化，理解每步逻辑：

步骤1：初始化栈（入度0的顶点压栈）

• 初始入度0的顶点：1（入度0）、2（入度0）；
• 栈S：[1, 2]（top=2）；count=0。

步骤2：弹出栈顶顶点2，处理邻接边

• 弹出2（top=1），输出“2 ”，count=1；
• 2的邻接顶点：4、5、7 → 入度各减1：
  • 4的入度：2→1；5的入度：2→1；7的入度：1→0；
• 7的入度变0，压栈 → 栈S：[1, 7]（top=2）。

步骤3：弹出栈顶顶点7，处理邻接边

• 弹出7（top=1），输出“2 7 ”，count=2；
• 7的邻接顶点：6 → 6的入度：2→1；
• 6的入度未到0，不压栈 → 栈S：[1]（top=1）。

步骤4：弹出栈顶顶点1，处理邻接边

• 弹出1（top=0），输出“2 7 1 ”，count=3；
• 1的邻接顶点：3 → 3的入度：1→0；
• 3的入度变0，压栈 → 栈S：[3]（top=1）。

步骤5：弹出栈顶顶点3，处理邻接边

• 弹出3（top=0），输出“2 7 1 3 ”，count=4；
• 3的邻接顶点：4 → 4的入度：1→0；
• 4的入度变0，压栈 → 栈S：[4]（top=1）。

步骤6：弹出栈顶顶点4，处理邻接边

• 弹出4（top=0），输出“2 7 1 3 4 ”，count=5；
• 4的邻接顶点：5、6 → 入度各减1：
  • 5的入度：1→0；6的入度：1→0；
• 5和6压栈 → 栈S：[5, 6]（top=2）。

步骤7：弹出栈顶顶点6，处理邻接边

• 弹出6（top=1），输出“2 7 1 3 4 6 ”，count=6；
• 6无邻接边 → 栈S：[5]（top=1）。

步骤8：弹出栈顶顶点5，处理邻接边

• 弹出5（top=0），输出“2 7 1 3 4 6 5 ”，count=7；
• 5无邻接边 → 栈空（top=0）。

最终结果

输出序列可能是“2 7 1 3 4 6 5”（拓扑序列不唯一，原文的“1 2 3 4 5 7 6”也正确，只要满足边的前后关系即可），count=7等于顶点数，无环。

五、新手避坑点（我踩过的坑，你别踩）

1. 语法错误：CreatGraph调用少逗号
   原文G=CreatGraph(G, n m) → 修正为G=CreatGraph(G, n, m)，否则编译报错“语法错误”；
2. 入度更新遗漏
   处理邻接顶点时忘记G.adjlist[k].in--，导致入度永远不为0，栈空后count<顶点数，误判有环；
3. 没有环的判断
   原文没写if (count < G.vertexNum)，无法检测环（比如图中有1→2、2→3、3→1，会输出部分顶点后停止，却不提示有环）；
4. 栈的初始化错误
   把S[++top]=i写成S[top++]=i，导致栈底元素存错，后续弹出顺序混乱。

六、总结：拓扑排序的实际价值

拓扑排序不只是实验题，在实际场景中超有用：

• 选课系统：先选无先修课的课程，解锁后续课程；
• 任务调度：项目开发中，先做“无前置任务”的模块（如先搭框架，再写功能）；
• 编译依赖：编译器先编译无依赖的文件，再编译依赖该文件的代码。

通过这个实验，不仅掌握了“入度+栈”实现拓扑排序的方法，还理解了邻接表在图存储中的优势——相比邻接矩阵，稀疏图用邻接表更省空间。