三次到达:理解二叉树非递归遍历
分析二叉树递归实现
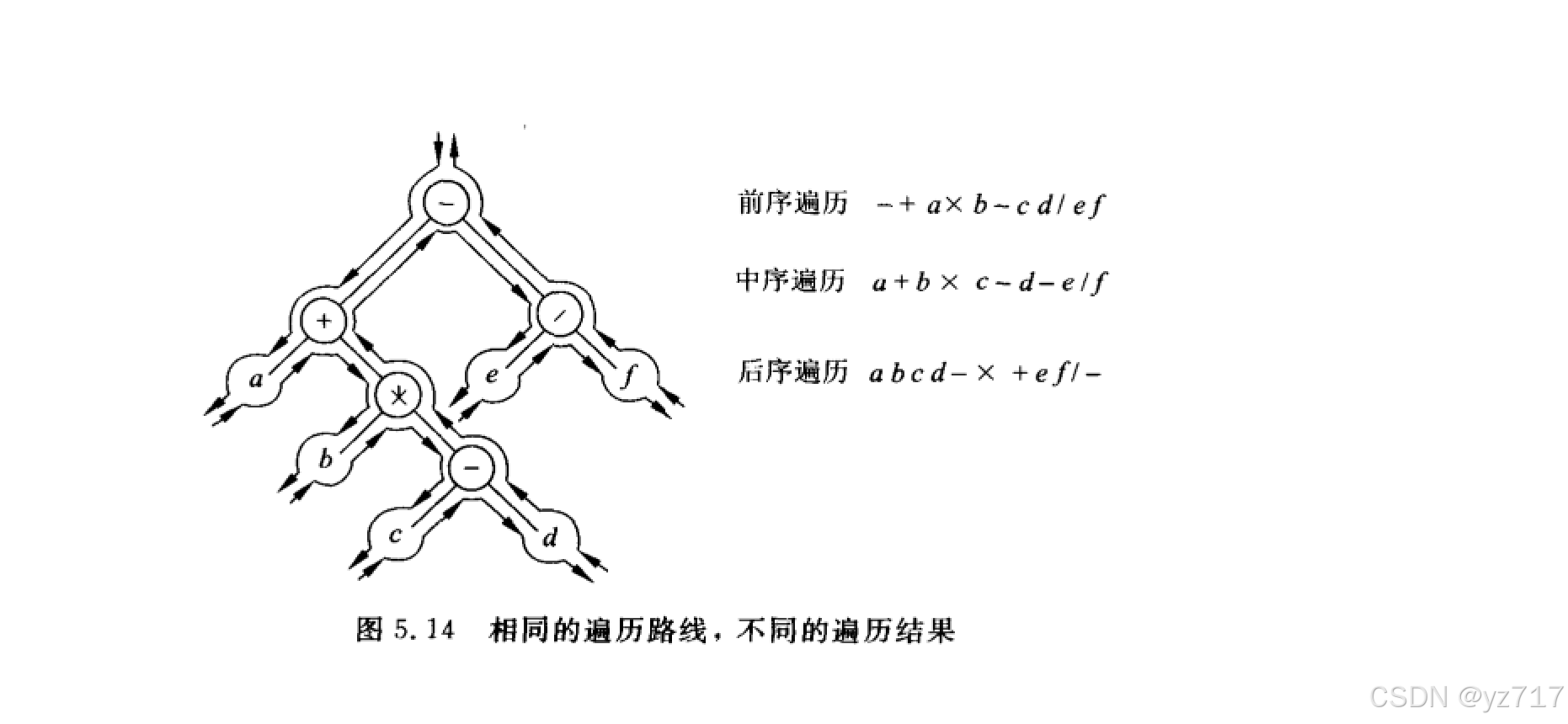
仔细分析二叉树的遍历,可以得到结论:
- 遍历的路线是相同的
- 不同的遍历结果取决与访问的时机
- 前序:第一次到达该节点访问
- 中序:第二次到达该节点访问
- 后续:第三次到达该节点访问
有了上面这个结论,其实就可以想办法去模拟这个遍历路线
路线分析
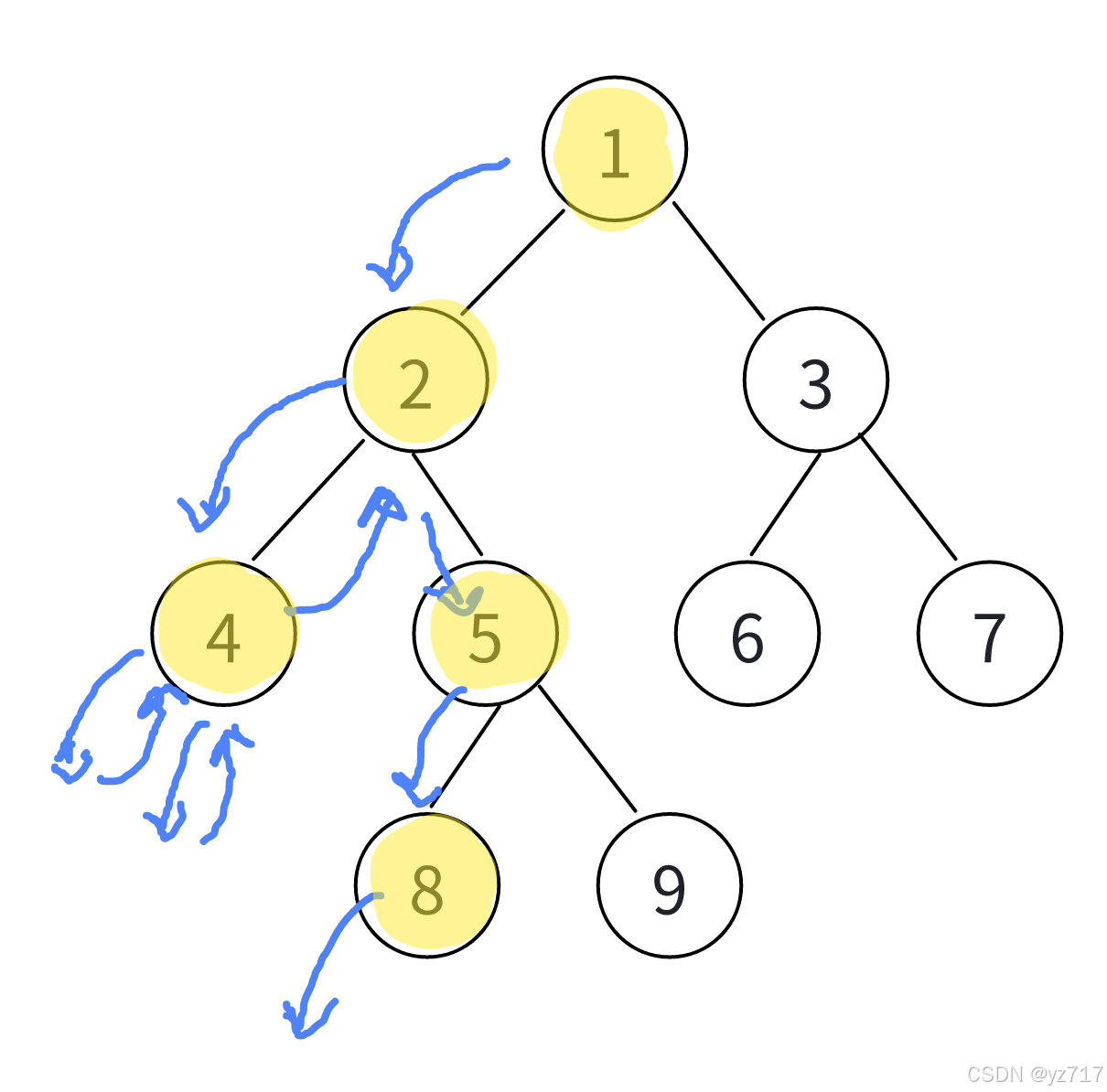
可以发现一个规律:
- 针对一颗二叉树,遍历路线是:一直走左边的节点,左边节点走完了,此时再走最后一个左节点的右子树
- 在处理右子树时还是依照上面的规律

模拟路线
模拟路线需要两个工具:
cur(探路先锋):表示“我当前正要处理的节点”st(记忆栈):模拟“函数调用栈”,帮我们“记住”回家的路(父节点)
依照上面的规律可以实现一个框架代码
while (cur || !st.empty()) {// 1. “一直走左边的节点”while (cur) {// ... (这是“第1次到达”,先别急着访问)st.push(cur); // 记住“回家的路”cur = cur->left; // 一直向左!}// 2. “左边节点走完了”(cur == null 了)// 我们从“记忆栈”里掏出“最后一个左节点”TreeNode* top = st.pop();// 3. “此时再走...右子树”// 我们准备去“top”的右子树探险cur = top->right; // 4. “在处理右子树时还是依照上面的规律”// (因为 cur = top->right, 循环回到顶部,// 又开始对这个“右子树”执行“一直走左边”)
}
前序遍历 (第 1 次到达时访问)
- 时机: “第一次到达”,也就是我们刚遇到这个节点,准备“一直向左”之前
- 代码:
vector<int> preorderTraversal(TreeNode* root) {vector<int> ret;stack<TreeNode*> st;TreeNode* cur = root;while(cur || !st.empty()) {// “一直走左边的节点”while(cur) {// >> 时机 1 <<// 第一次到达!立刻访问!ret.push_back(cur->val); st.push(cur); // 记住回家的路cur = cur->left; // 走左}// “左边走完了”TreeNode* top = st.top();st.pop();// “去右边”cur = top->right;}return ret;
}
中序遍历 (第 2 次到达时访问)
- 时机: “第二次到达”,也就是“左边走完了 (
cur == null)”,我们从“记忆栈”里pop出它的时候 - 代码:
vector<int> inorderTraversal(TreeNode* root) {vector<int> ret;stack<TreeNode*> st;TreeNode* cur = root;while(cur || !st.empty()) {// “一直走左边的节点”while(cur) {st.push(cur);cur = cur->left;}// “左边走完了”(cur == null)TreeNode* top = st.top(); // pop!st.pop();// >> 时机 2 <<// 从“左边”回来了!立刻访问!ret.push_back(top->val);// “去右边”cur = top->right;}return ret;
}
后序遍历 (第 3 次到达时访问)
- 时机: “第三次到达”,也就是从“右子树”也回来之后
- 挑战: 当我们
pop(top)时,我们只知道是“第 2 次到达”(从左边回来)。我们必须先去top->right。只有当top->right也处理完了,我们才能访问top - 怎么办?
- 我们
pop之前,先top()“偷看一下”。 top就是我们“第 2 次”到达的节点。- 我们问:它的“右子树” (
top->right) 处理完了吗?- A: 如果
top->right == nullptr(没右子树),那“第 3 次”和“第 2 次”是同时的。可以访问! - B: 如果
top->right刚被处理过,那也可以访问!
- A: 如果
- 如何知道“刚被处理过”?我们引入一个
prev指针,记录“上一个被访问的节点”。如果top->right == prev,就说明“右边”刚回来!
- 我们
- 代码:
vector<int> postorderTraversal(TreeNode* root) { vector<int> ret;stack<TreeNode*> st;TreeNode* cur = root;TreeNode* prev = nullptr; // 记录“上一个被访问的节点”while(cur || !st.empty()) {// “一直走左边的节点”while(cur) {st.push(cur);cur = cur->left;}// “左边走完了”(cur == null)// 先不 pop!先“偷看”!TreeNode* top = st.top();// >> 时机 2 (决策点) <<// 我们在“第 2 次”到达 top// 我们要判断“右边”去过了吗?if (top->right == nullptr || top->right == prev) {// A: 没右子树 (第 2、3 次同时)// B: 右子树刚回来 (这就是第 3 次)// >> 时机 3 <<// 访问!ret.push_back(top->val);st.pop(); // 真正“出栈”prev = top; // 记录“我刚访问了 top”// cur 保持为 null,以便下一轮继续“pop”}else {// “右边”还没去过!// 必须先去“右边”!cur = top->right;}}return ret;
}
总结:真正需要记住的
只需要“理解”这**“一套理论”**:
-
路线模拟:我们用
cur(探路)和st(记忆)来模拟这个路线 -
代码框架:
cur == nullptr && st.empty()为结束条件,然后一直往左走,最后再转向右 -
时机安插:
- 前序:
push时访问 - 中序:
pop时访问
要“理解”这**“一套理论”**:
- 前序:
-
路线模拟:我们用
cur(探路)和st(记忆)来模拟这个路线 -
代码框架:
cur == nullptr && st.empty()为结束条件,然后一直往左走,最后再转向右 -
时机安插:
- 前序:
push时访问 - 中序:
pop时访问 - 后序:
pop前“偷看”,用prev判断“右边”是否回来,再访问
- 前序:
