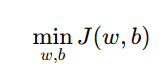机器学习（2） 线性回归和代价函数
一、线性回归（Linear Regression）
1. 基本概念（Basic Concept）
线性回归（Linear Regression） 是一种典型的 监督学习（Supervised Learning） 方法。
它通过给定带有正确答案（标签）的训练数据，学习输入特征与输出目标之间的线性关系。
目标（Goal）：
学习一个函数 f(x)，使得模型预测值 y^=f(x) 尽可能接近真实值 y。
2. 监督学习的基本流程（Supervised Learning Workflow）
（1）输入特征和输出目标（Input Features & Targets）
给模型一组训练数据（training set）
(x(1),y(1)),(x(2),y(2)),…,(x(m),y(m))例如：
x(2)：第二个样本的输入（如房屋面积）
y(2)：第二个样本的输出（如房价）
（2）输入学习算法（Feed Data into Learning Algorithm）
算法通过训练数据学习输入与输出的映射关系。
（3）得到模型函数 fff（Learn a Model Function）
学习得到函数 f，它能根据输入 x 输出预测值 y^：
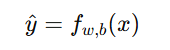
3. 线性回归的数学形式（Mathematical Form）
（1）单变量线性回归（Univariate Linear Regression）
当输入特征只有一个时（例如房屋面积 → 房价），模型为：
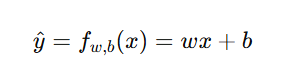
其中：
| 符号 | 含义 |
|---|---|
| x | 输入特征（feature） |
| y | 真实输出（target/label） |
| y^ | 预测输出（predicted value） |
| w | 权重（weight），控制直线的斜率 |
| b | 偏置（bias/intercept），控制直线的位置 |
模型是一条直线（linear function），形状简单、易于计算。
之后可以扩展到更复杂的 非线性模型（nonlinear models）。
（2）多变量线性回归（Multivariate Linear Regression）
当输入有多个特征时（例如房屋面积、卧室数量、距离市中心等），模型变为：
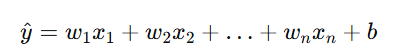
或向量形式：
4. 模型的目标与损失函数（Objective & Loss Function）
目标：
找到最优的 w 和 b，使预测值 y^ 尽可能接近真实值 y。
误差（Error）：
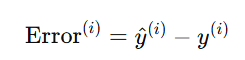
损失函数（Loss Function） — 常用为 均方误差（Mean Squared Error, MSE）：
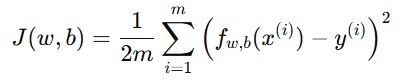
目标是最小化损失函数：
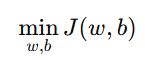
5. 参数学习方法（Parameter Learning Methods）
（1）解析解（Analytical Solution）
对小规模数据可直接求出最优解：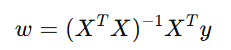
适合特征数量不多时使用。
（2）梯度下降（Gradient Descent）
对大规模数据更常用的优化方法：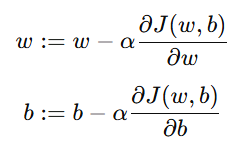
其中 α 为学习率（Learning Rate），控制每次更新的步长。
6. 应用实例（Applications）
| 应用场景 | 说明 |
|---|---|
| 房价预测（House Price Prediction） | 输入房屋特征，输出预测价格 |
| 销售预测（Sales Forecasting） | 输入广告投入、季节等特征 |
| 学生成绩预测（Student Score Prediction） | 输入学习时间，输出考试成绩 |
| 工业测量（Industrial Measurement） | 根据传感器数据预测产量或能耗 |
7. 模型优缺点（Advantages & Disadvantages）
| 优点（Advantages） | 缺点（Disadvantages） |
|---|---|
| 模型简单、计算高效 | 只能捕捉线性关系 |
| 可解释性强（每个参数含义明确） | 对异常值敏感（outliers） |
| 可作为其他算法的基础（如逻辑回归） | 对特征尺度敏感（需标准化） |
8. 小结（Summary）
| 项目 | 内容 |
|---|---|
| 模型形式 |  |
| 学习类型 | 监督学习（Supervised Learning） |
| 目标 | 最小化预测误差（Minimize Prediction Error） |
| 损失函数 | 均方误差（MSE） |
| 训练方法 | 梯度下降 / 解析解 |
| 典型应用 | 房价预测、成绩预测 |
二、代价函数 J（Cost Function）
（1） 定义（Definition）
在监督学习中，特别是线性回归（Linear Regression）里，我们需要一种方式来衡量模型预测值与真实值之间的差距。这个衡量误差的函数就是代价函数（Cost Function）。
符号表示：
J(w,b)或简写为 J(w)（当只考虑 w ，b为0时）
含义：
它表示当模型参数为 w,bw, bw,b 时，所有训练样本预测误差的平均程度。我们希望通过训练，使 J(w,b)J(w,b)J(w,b) 尽可能小。
（2） 数学表达式（Mathematical Expression）
在线性回归模型中：
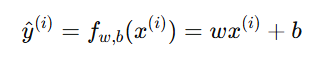
代价函数（Cost Function）使用均方误差（Mean Squared Error, MSE）形式：
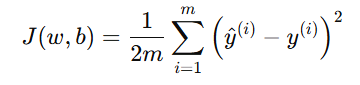
或写作：
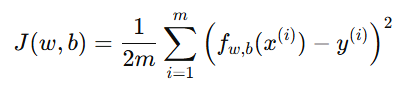
其中：
| 符号 | 含义 |
|---|---|
| m | 训练样本数量 |
| x(i) | 第 i 个输入样本 |
| y(i) | 第 i 个真实输出 |
| y^(i) | 模型预测值 |
| w,b | 模型参数 |
| J(w,b) | 代价函数，衡量整体误差的平均值 |
说明：
前面的「1/2」系数不是必须的，只是为了后续求导时公式更简洁。
（3） 使用目的（Purpose）
在线性回归中，我们的训练目标（training objective）就是：
最小化代价函数：
即寻找最优的 w,b，使模型的预测误差最小。
当 J(w,b) 越小 → 模型预测越准确
当 J(w,b) 过大 → 模型预测与实际偏差较大
这种思想称为：
最小二乘法（Least Squares Method）
（4） 如何利用代价函数找到最优参数（Finding Optimal w and b）
我们可以通过优化算法（Optimization Algorithm）不断调整参数 w 和 b，
使 J(w,b) 逐步减小。
最常见的方法是：
梯度下降（Gradient Descent）
基本思想：
计算当前参数下的代价函数值 J(w,b)；
计算 JJJ 对参数的偏导（梯度）；
按负梯度方向更新参数；
不断重复，直到 J(w,b) 收敛到最小值。
更新公式：
其中：
α：学习率（Learning Rate）
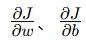：梯度（gradients）
（5） 三维可视化代价函数（3D Visualization of J）
在线性回归中，若参数只有两个（w 和 b），
我们可以将代价函数 J(w,b) 看作一个三维曲面（3D surface）：
横轴：参数 w
纵轴：参数 b
高度：代价函数值 J(w,b)
可视化结果：
曲面形状通常是一个凸碗（convex bowl）。
曲面最低点对应 J(w,b) 的最小值。
在该点上，模型参数 (w∗,b∗) 是最优参数（optimal parameters）。
理解：
梯度下降算法的过程就像一个小球沿着碗壁不断滚动，最终停在碗底的最低点（最优解）。
（6） 等高线图可视化（Contour Plot Visualization）
等高线图（Contour Plot） 是三维代价函数在二维平面上的投影，可以更直观地理解参数更新的过程。
每一条曲线代表代价函数 J(w,b) 的一个固定值。
曲线越靠近中心，表示 J(w,b) 越小。
梯度下降的更新轨迹会在图中呈现为一条向圆心收敛的路径。
示意：
等高线图（Contour Plot）高 J(w,b)▲│○ ○ ○ ○ ○○ ○ ○ ○ ○○ ○ ○ ○ ○ ← 梯度下降的路径从外向内收敛●▼最小 J(w,b)
（7） 小结（Summary）
| 项目 | 内容 |
|---|---|
| 名称 | 代价函数（Cost Function） |
| 作用 | 衡量模型预测与真实值之间的整体误差 |
| 常见形式 | 均方误差 MSE |
| 表达式 |  |
| 目标 | 最小化 J(w,b） |
| 优化方法 | 梯度下降（Gradient Descent） |
| 可视化 | 三维曲面图 + 等高线图 |