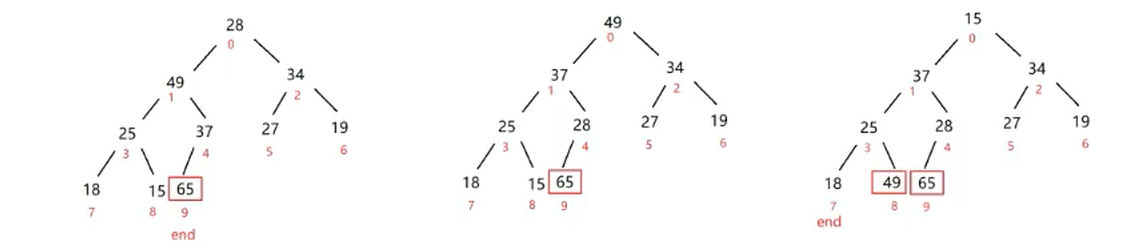
优先级队列的学习(二)

创建堆

上一节优先队列的学习讲过了，我们再看看代码
这是换一种写法的代码

public static void createHeap(int[] array) {// 找到倒数第一个非叶子节点的索引int root = ((array.length - 2) >> 1); // 从该节点开始，向前遍历到根节点（索引0），每个节点执行向下调整for (; root >= 0; root--) {shiftDown(array, root); }
}

int root = ((array.length - 2) >> 1);
作用：计算最后一个非叶子节点的索引。
原理：
数组长度为 array.length，最后一个元素的索引是 array.length - 1。
根据完全二叉树的性质，非叶子节点的子节点索引 = 2 * 父节点索引 + 1（左孩子） 或 2*父节点索引 + 2（右孩子）。
反推：最后一个非叶子节点的索引 = (最后一个元素索引 - 1) / 2，即 (array.length - 1 - 1) / 2 = (array.length - 2) / 2。

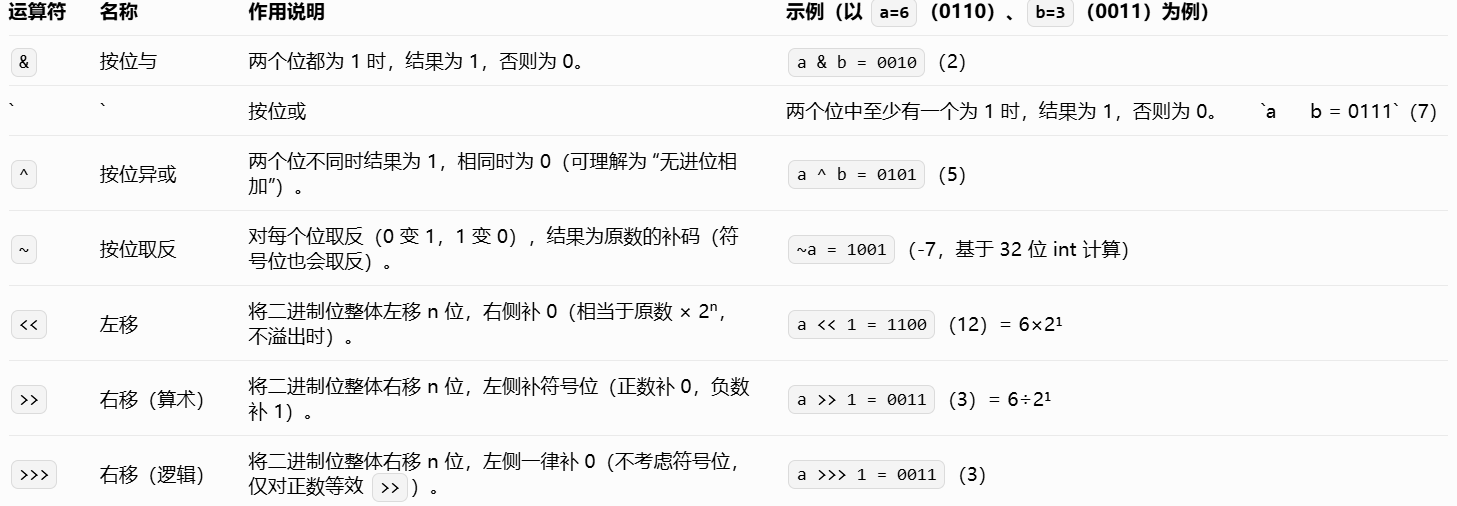
1 是位运算，等价于整数除法 / 2（效率更高），因此 (array.length - 2) >> 1 与 (array.length - 2) / 2 结果相同。
举例：若数组长度为 6（索引 0~5），最后一个非叶子节点索引 = (6-2)/2 = 2（正确，节点 2 的子节点是 4 和 5）。

运算符：左移（<<）一位相当于对原数乘以 2 的一次方
，右移（>> 或 >>>）一位相当于对原数除以 2的一次方（整数除法，向下取整）。

public static void createHeap(int[] array) {// 找到倒数第一个非叶子节点的索引int root = ((array.length - 2) >> 1); // 从该节点开始，向前遍历到根节点（索引0），每个节点执行向下调整for (; root >= 0; root--) {shiftDown(array, root); }
}

用大堆创建
向下（下沉）

public class HeapCreator {// 大根堆的向下调整：确保父节点 >= 子节点private void shiftDownMax(int[] array, int parent, int len) {int child = 2 * parent + 1; // 左孩子索引while (child < len) {// 找左右孩子中更大的那个if (child + 1 < len && array[child + 1] > array[child]) {child++;}// 父节点 >= 最大子节点，满足大根堆if (array[parent] >= array[child]) {break;}// 交换父节点与最大子节点int temp = array[parent];array[parent] = array[child];array[child] = temp;// 继续向下调整parent = child;child = 2 * parent + 1;}}// 创建大根堆public void buildMaxHeap(int[] array) {int n = array.length;// 从最后一个非叶子节点开始，向前调整所有非叶子节点for (int parent = (n - 2) / 2; parent >= 0; parent--) {shiftDownMax(array, parent, n);}}public static void main(String[] args) {int[] arr = {3, 1, 2, 7, 5, 4};new HeapCreator().buildMaxHeap(arr);// 输出：7 5 4 3 1 2（满足大根堆性质）for (int num : arr) {System.out.print(num + " ");}}
}

向上的

public class MaxHeapWithShiftUp {private int[] heap;   private int size;      private int capacity; // 初始化大根堆public MaxHeapWithShiftUp(int capacity) {this.capacity = capacity;this.heap = new int[capacity];this.size = 0;}// 大根堆的向上调整：新元素插入后上浮private void shiftUp(int child) {int parent = (child - 1) / 2;  // 计算父节点索引// 循环条件：子节点不是根节点，且子节点值 > 父节点值（破坏大根堆性质）while (child > 0 && heap[child] > heap[parent]) {// 交换子节点与父节点（大值上浮）swap(child, parent);// 向上移动：子节点指向原父节点，重新计算父节点child = parent;parent = (child - 1) / 2;}}// 插入元素到大根堆public void insert(int value) {if (size == capacity) {throw new RuntimeException("堆已满，无法插入");}// 新元素放到堆的末尾heap[size] = value;// 对新元素执行向上调整shiftUp(size);size++;  // 元素个数加1}// 交换元素private void swap(int i, int j) {int temp = heap[i];heap[i] = heap[j];heap[j] = temp;}// 获取堆顶元素（最大值）public int peek() {if (size == 0) {throw new RuntimeException("堆为空");}return heap[0];}// 测试public static void main(String[] args) {MaxHeapWithShiftUp maxHeap = new MaxHeapWithShiftUp(10);// 插入元素maxHeap.insert(3);maxHeap.insert(1);maxHeap.insert(2);maxHeap.insert(7);maxHeap.insert(5);maxHeap.insert(4);System.out.println("堆顶元素（最大值）：" + maxHeap.peek()); // 输出：7System.out.print("堆元素：");for (int i = 0; i < maxHeap.size; i++) {System.out.print(maxHeap.heap[i] + " "); // 输出：7 5 4 3 1 2}}
}

用小堆创建
向下的（下沉）

public class MinHeapCreator {// 小根堆的向下调整：确保父节点 <= 子节点private void shiftDownMin(int[] array, int parent, int len) {int child = 2 * parent + 1; // 左孩子索引while (child < len) {// 找左右孩子中更小的那个（若右孩子存在且更小，则标记右孩子）if (child + 1 < len && array[child + 1] < array[child]) {child++;}// 父节点 <= 最小子节点，满足小根堆性质，无需调整if (array[parent] <= array[child]) {break;}// 交换父节点与最小子节点（父节点下沉）int temp = array[parent];array[parent] = array[child];array[child] = temp;// 继续向下调整（父节点移至子节点位置，更新子节点索引）parent = child;child = 2 * parent + 1;}}// 创建小根堆public void buildMinHeap(int[] array) {int n = array.length;// 从最后一个非叶子节点开始，向前调整所有非叶子节点for (int parent = (n - 2) / 2; parent >= 0; parent--) {shiftDownMin(array, parent, n);}}public static void main(String[] args) {int[] arr = {3, 1, 2, 7, 5, 4};new MinHeapCreator().buildMinHeap(arr);// 输出：1 3 2 7 5 4（满足小根堆性质：堆顶为最小值，父节点 <= 子节点）for (int num : arr) {System.out.print(num + " ");}}
}
向上的（上浮）```java
public class MinHeapWithShiftUp {private int[] heap; private int size;   private int capacity; // 初始化堆public MinHeapWithShiftUp(int capacity) {this.capacity = capacity;this.heap = new int[capacity];this.size = 0;}// 小根堆的向上调整：插入新元素后，将其上浮到合适位置private void shiftUp(int child) {int parent = (child - 1) / 2; // 计算父节点索引// 循环条件：子节点不是根节点，且子节点值 < 父节点值（不满足小根堆性质）while (child > 0 && heap[child] < heap[parent]) {// 交换子节点与父节点（小值上浮）swap(child, parent);// 向上移动：子节点指向原父节点，重新计算父节点child = parent;parent = (child - 1) / 2;}}// 插入元素到小根堆public void insert(int value) {if (size == capacity) {throw new RuntimeException("堆已满，无法插入");}// 插入到堆的末尾heap[size] = value;// 对新插入的元素执行向上调整shiftUp(size);size++; // 元素个数加1}// 交换两个索引的元素private void swap(int i, int j) {int temp = heap[i];heap[i] = heap[j];heap[j] = temp;}// 获取堆顶元素（最小值）public int peek() {if (size == 0) {throw new RuntimeException("堆为空");}return heap[0];}// 测试public static void main(String[] args) {MinHeapWithShiftUp minHeap = new MinHeapWithShiftUp(10);// 插入元素minHeap.insert(3);minHeap.insert(1);minHeap.insert(2);minHeap.insert(7);minHeap.insert(5);minHeap.insert(4);// 输出堆顶元素（应为最小值1）System.out.println("堆顶元素：" + minHeap.peek()); // 输出：1// 打印堆中的元素（顺序为数组存储的小根堆结构）System.out.print("堆元素：");for (int i = 0; i < minHeap.size; i++) {System.out.print(minHeap.heap[i] + " "); // 输出：1 3 2 7 5 4}}
}

## 堆的调整
调整步骤
**初始化标记：**
parent 标记需要调整的节点（如根节点）。
child 标记 parent 的左孩子（child = 2*parent + 1，因为完全二叉树中，若有孩子，左孩子一定存在）。
**循环调整（直到 parent 无左孩子）：**
若右孩子存在（child+1 < size），比较左右孩子大小，让 child 标记值更小的孩子。
比较 parent 与 child 的值：
若 parent 的值 ≤ child 的值：满足小根堆性质，调整结束。
否则：交换 parent 与 child，然后将 parent 指向 child，child 更新为新 parent 的左孩子（child = 2*parent + 1），继续循环。
**小根堆的向下调整**```java
/*** 小根堆的向下调整* @param array 待调整的数组* @param parent 需要调整的节点索引*/
public void shiftDown(int[] array, int parent) {// child先标记parent的左孩子，因为parent可能有左没有右int child = 2 * parent + 1;int size = array.length;
//如果右孩子不存在，那直接标记他，不会执行if有孩子的这一部分while (child < size) {// 如果右孩子存在，找到左右孩子中较小的孩子，用child进行标记if (child + 1 < size && array[child + 1] < array[child]) {child += 1;}// 如果双亲比其最小的孩子还小，说明该结构已经满足堆的特性了if (array[parent] <= array[child]) {break;} else {// 将双亲与较小的孩子交换int t = array[parent];array[parent] = array[child];array[child] = t;// parent中大的元素往下移动，可能会造成子树不满足堆的性质，因此需要继续向下调整parent = child;child = parent * 2 + 1;}}
}

大堆的向下调整：

/*** 大根堆的向下调整* @param array 待调整的数组* @param parent 需要调整的节点索引*/
public void shiftDownMax(int[] array, int parent) {int child = 2 * parent + 1; // 先标记左孩子（完全二叉树中左孩子优先存在）int size = array.length;while (child < size) { // 左孩子存在时才需要调整// 若右孩子存在，且右孩子的值 > 左孩子的值，则child标记右孩子（找更大的孩子）if (child + 1 < size && array[child + 1] > array[child]) {child++;}// 若父节点的值 >= 最大孩子的值，满足大根堆，退出if (array[parent] >= array[child]) {break;} else {// 交换父节点与最大孩子（将大值上移）int temp = array[parent];array[parent] = array[child];array[child] = temp;// 继续向下调整：父节点移到child位置，child更新为新父节点的左孩子parent = child;child = 2 * parent + 1;}}
}

大根堆的向下调整逻辑与小根堆类似，核心区别在于：比较时需找到左右孩子中值更大的那个，并确保父节点的值大于等于孩子节点的值。
向上调整
核心逻辑：新元素从底层向上比较，若不满足堆的父子关系（如大根堆中子节点大于父节点），则与父节点交换，直到找到合适位置或成为根节点。
大根堆的向上调整的步骤

• 新元素插入到堆的末尾（数组最后一个位置），记为 child（子节点索引）。

• 计算其父节点索引 parent = (child - 1) / 2。

• 比较 child 与 parent 的值：

• 若 child 的值 > parent 的值（大根堆不满足）：交换两者，child 指向原 parent 的位置，重复步骤 2~3。

• 若 child 的值 ≤ parent 的值（满足大根堆）：调整结束。

/*** 大根堆的向上调整（插入新元素后）* @param array 堆的数组* @param child 新元素的索引（初始为数组末尾）*/
public void shiftUp(int[] array, int child) {int parent = (child - 1) / 2; // 计算父节点索引while (child > 0) { // 子节点不是根节点时继续// 大根堆：若子节点 > 父节点，交换if (array[child] > array[parent]) {int temp = array[child];array[child] = array[parent];array[parent] = temp;// 向上移动：子节点指向父节点，重新计算父节点child = parent;parent = (child - 1) / 2;} else {// 满足大根堆性质，退出break;}}
}

小根堆的向上调整
小根堆的向上调整只需将 “子节点> 父节点” 改为 “子节点 < 父节点”：

public void shiftUpMin(int[] array, int child) {int parent = (child - 1) / 2;while (child > 0) {// 小根堆：若子节点 < 父节点，交换if (array[child] < array[parent]) {int temp = array[child];array[child] = array[parent];array[parent] = temp;child = parent;parent = (child - 1) / 2;} else {break;}}
}

插入与删除

堆的插入
堆的插入总共需要两个步骤：
先将元素放入到底层空间中（注意：空间不够时需要扩容）
将最后新插入的节点向上调整，直到满足堆的性质

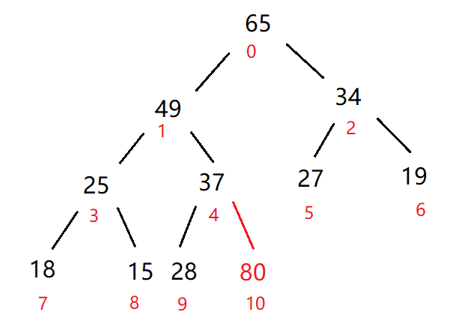
比如我要插入80这个这个值，使用大堆的向上调整方法

import java.util.Arrays;public class MaxHeap {private int[] elem;private int usedSize;public MaxHeap() {this.elem = new int[10]; this.usedSize = 0;}public void offer(int val) {if (isFull()) {elem = Arrays.copyOf(elem, 2 * elem.length);}elem[usedSize] = val;siftUp(usedSize);usedSize++;}private void siftUp(int child) {int parent = (child - 1) / 2;while (parent >= 0) {if (elem[child] > elem[parent]) {swap(child, parent);child = parent;parent = (child - 1) / 2;} else {break;}}}private void swap(int i, int j) {int temp = elem[i];elem[i] = elem[j];elem[j] = temp;}public boolean isFull() {return usedSize == elem.length;}// 测试方法public static void main(String[] args) {MaxHeap maxHeap = new MaxHeap();maxHeap.offer(10);maxHeap.offer(20);maxHeap.offer(5);maxHeap.offer(30);// 此时堆中元素应满足大根堆性质，根节点为30for (int i = 0; i < maxHeap.usedSize; i++) {System.out.print(maxHeap.elem[i] + " ");}}
}

小堆插入向上调整的方法
就是比较的大小不一样

/*** 小根堆的向上调整（用于插入新元素后恢复堆性质）* @param array 存储堆的数组* @param child 新插入元素的索引（初始为数组末尾）*/
public void shiftUpMin(int[] array, int child) {// 计算父节点索引int parent = (child - 1) / 2;// 循环条件：子节点不是根节点（child > 0）while (child > 0) {// 小根堆：若子节点 < 父节点，说明不满足堆性质，需要交换if (array[child] < array[parent]) {// 交换子节点与父节点int temp = array[child];array[child] = array[parent];array[parent] = temp;// 向上移动：子节点指向原父节点位置，重新计算父节点child = parent;parent = (child - 1) / 2;} else {// 子节点 >= 父节点，满足小根堆性质，退出调整break;}}
}// 小根堆插入元素的完整方法（包含扩容判断）
public void insertMinHeap(int[] array, int value, int size) {// 假设array容量足够，直接插入到末尾（实际需判断扩容）array[size] = value;// 对新插入的元素执行向上调整shiftUpMin(array, size);
}

堆的删除
堆的删除操作通常指删除堆顶元素（大根堆的最大值或小根堆的最小值）
核心逻辑是通过 “覆盖堆顶 + 向下调整” 来恢复堆的性质，具体步骤：

堆删除的完整逻辑（以大根堆为例）

• 判断堆是否为空：若堆中无元素，直接返回（或抛出异常）。

用最后一个元素覆盖堆顶：

• 将堆的最后一个元素（数组末尾元素）赋值给堆顶（索引 0），然后删除最后一个元素（有效长度减 1）。（目的：快速移除堆顶，同时避免堆结构断裂）。
  从堆顶执行向下调整：
• 由于新堆顶可能破坏堆的性质（如大根堆中，新堆顶的值可能小于子节点），需对新堆顶执行向下调整，使其与子节点比较并交换，直到整个堆重新满足性质。
  
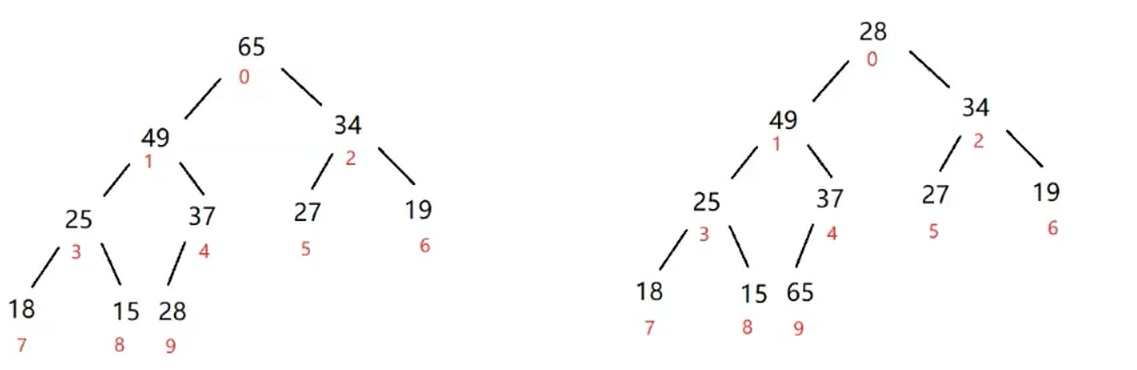
  就是换完就是这个效果，而且也不是彻底删除，只是最后一个和堆顶的元素交换了位置，然后进行将有效usedSize 进行-1 ，对他覆盖。

   private void shiftDown(int parent, int len) {int child = 2 * parent + 1;while (child < len) {// 找左右孩子中更大的那个if (child + 1 < len && elem[child + 1] > elem[child]) {child++;}// 父节点 >= 最大子节点，满足堆性质if (elem[parent] >= elem[child]) {break;}// 交换并继续调整swap(parent, child);parent = child;child = 2 * parent + 1;}}private void swap(int i, int j) {int temp = elem[i];elem[i] = elem[j];elem[j] = temp;}// 堆的删除操作（删除堆顶元素）public int remove() {//当然这里也可以再写一个判断是否为空的方法if (usedSize == 0) {throw new RuntimeException("堆为空，无法删除");}// 1. 保存堆顶元素（要返回的值）int top = elem[0];// 2. 用最后一个元素覆盖堆顶elem[0] = elem[usedSize - 1];usedSize--; // 有效长度减1（逻辑删除最后一个元素）// 从堆顶进行向下调整，恢复堆性质shiftDown(0, usedSize);return top;}
}

用堆模拟实现优先级队列

import java.util.Arrays;public class TestHeap {public int[] elem;public int usedSize;public TestHeap() {this.elem = new int[10];}public void initArray(int[] array) {for (int i = 0; i < array.length; i++) {elem[i] = array[i];usedSize++;}}/*** 创建大根堆* 向下调整的方式：时间复杂度：O(N)*/public void createHeap() {for (int parent = (usedSize-1-1)/2; parent >= 0; parent--) {siftDown(parent,usedSize);}}/*** 向下调整的方法* @param parent 每棵子树的根节点下标* @param usedSize 每棵子树是否调整结束的位置*/private void siftDown(int parent, int usedSize) {int child = 2 * parent + 1;//说明 至少有一个左孩子//至少有一个左孩子//elem[child + 1]这里可能会产生child + 1 的空
//             if(elem[child] < elem[child + 1]){
//                 child++;
//             }while (child < usedSize) {if(child+1 < usedSize && elem[child] < elem[child+1]) {child++;}//代码走到这里 表示 child下标 一定是最大孩子的下标if(elem[child] > elem[parent]) {//交换swap(child,parent);parent = child;child = 2*parent+1;}else {break;}}}private void swap(int i,int j) {int tmp = elem[i];elem[i] = elem[j];elem[j] = tmp;}/*** 插入元素* @param val*/public void offer(int val) {if(isFull()) {elem = Arrays.copyOf(elem,2*elem.length);}elem[usedSize] = val;//向上 调整siftUp(usedSize);usedSize++;}/*** 向上调整* @param child*/private void siftUp(int child) {int parent = (child-1)/2;while (parent >= 0) {if(elem[child] > elem[parent]) {swap(child,parent);child = parent;parent = (child-1)/2;}else {break;}}}public boolean isFull() {return usedSize == elem.length;}/*** 删除的逻辑* @return*/public int poll() {if(isEmpty()) {return -1;}int val = elem[0];swap(0,usedSize-1);usedSize--;siftDown(0,usedSize);return val;}public boolean isEmpty() {return usedSize == 0;}/*** 获取优先级队列 堆顶元素* @return*/public int peek() {if(isEmpty()) {return -1;}return elem[0];}//O(n*logN)public void heapSort() {int end = usedSize-1;while (end > 0) {swap(0,end);siftDown(0,end);end--;}}}//Test
import java.util.Comparator;
import java.util.PriorityQueue;class Student implements Comparable<Student>{public int age;public Student(int age) {this.age = age;}@Overridepublic int compareTo(Student o) {//return this.age - o.age;return o.age - this.age;}@Overridepublic String toString() {return "Student{" +"age=" + age +'}';}
}class ImpMaxComparator implements Comparator<Integer> {@Overridepublic int compare(Integer o1, Integer o2) {//return o1.compareTo(o2);return o2.compareTo(o1);}
}class ImpMinComparator implements Comparator<Integer> {@Overridepublic int compare(Integer o1, Integer o2) {return o1.compareTo(o2);}
}public class Test {public int[] smallestK(int[] array, int k) {if(array == null || k <= 0) {return null;}ImpMaxComparator impMaxComparator = new ImpMaxComparator();PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(impMaxComparator);//1,把前K个元素 创建成 大根堆for(int i = 0;i < k;i++) {priorityQueue.offer(array[i]);}//遍历剩下的N-K个元素for (int i = k; i < array.length; i++) {int peekVal = priorityQueue.peek();if(peekVal > array[i]) {priorityQueue.poll();priorityQueue.offer(array[i]);}}int[] ret = new int[k];for (int i = 0; i < k; i++) {ret[i] = priorityQueue.poll();}return ret;}public static void main(String[] args) {ImpMaxComparator impMaxComparator = new ImpMaxComparator();ImpMinComparator impMinComparator = new ImpMinComparator();PriorityQueue<Integer> priorityQueue = new PriorityQueue<>(impMinComparator);priorityQueue.offer(12);priorityQueue.offer(5);priorityQueue.offer(9);priorityQueue.offer(100);System.out.println(priorityQueue.peek());/*PriorityQueue<Student> priorityQueue2 = new PriorityQueue<>();priorityQueue2.offer(new Student(12));priorityQueue2.offer(new Student(5));System.out.println(priorityQueue2.peek());
*/}public static void main1(String[] args) {TestHeap testHeap = new TestHeap();int[] array = {27,15,19,18,28,34,65,49,25,37};testHeap.initArray(array);testHeap.createHeap();testHeap.heapSort();/*for (int i = 0; i < array.length; i++) {testHeap.offer(array[i]);}*///System.out.println(testHeap.poll());//65}}

堆的应用

注意：堆的删除⼀定删除的是堆顶元素。具体如下：
1.将堆顶元素对堆中最后⼀个元素交换
2.将堆中有效数据个数减少⼀个
3.对堆顶元素进行向下调整