当前位置： 首页 > news >正文

《从理论到实践：红黑树的自平衡机制与C++高效实现指南》

news 2025/10/19 6:39:59

前言：在计算机科学领域，数据结构的选择直接决定着算法性能的巅峰。红黑树——这一被誉为"最优雅的平衡二叉搜索树"，凭借其严格的平衡约束和稳定的对数级时间复杂度（O(log n)），已成为高性能系统的核心支柱。从Linux内核的进程调度到C++ STL的map容器，从数据库引擎的B+树后备存储到实时系统的内存管理，红黑树的身影无处不在。

目录

一、红黑树的定义

二、红黑树的性质

三、红黑树实现的总体思路

四、红黑树的节点结构

五、红黑树的插入操作

1.按照二叉搜索的树规则插入新节点

2.检测新节点插入后，红黑树的性质是否造到破坏

情况一: cur为红，p为红，g为黑，u存在且为红

情况二: cur为红，p为红，g为黑，u不存在/u存在且为黑

情况三: cur为红，p为红，g为黑，u不存在/u存在且为黑

六、红黑树的验证

总代码

一、红黑树的定义

红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或 Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路 径会比其他路径长出俩倍，因而是接近平衡的。

二、红黑树的性质

1.每个结点不是红色就是黑色

红黑树的每个节点都有颜色属性：红和黑。不允许出现其它颜色情况

2.根节点是黑色的

整棵红黑树的根节点必须是黑色

3.如果一个节点是红色的，则它的两个孩子结点是黑色的

也就是说，父子节点不可能出现连续的红色

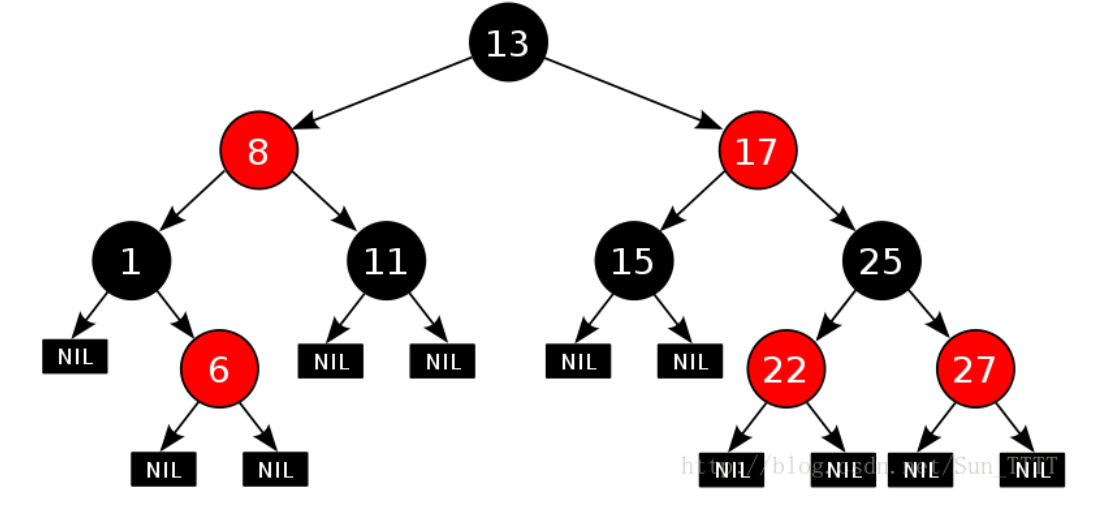
4.每个叶子节点都是黑色的

红黑树的叶子节点通常定义为 NIL（空节点），即使实际树中不画，需视为黑色节点

5.对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点

简单路径​：树中不重复经过节点的路径（从当前节点到任意叶子节点的路径唯一）

想象从任意节点出发，沿着所有可能的路径走向叶子节点（NIL节点），每条路径经过的黑色节点数量必须完全相同。这个统一的计数被称为该节点的黑高（Black Height）。

以节点X为起点，可能存在多条通往不同NIL叶子的路径
路径可能经过不同数量的红色节点
但所有路径中的黑色节点总数必须严格一致

     B(黑)/   \R(红)  B(黑)/  \    /  \
NIL NIL NIL NIL

如上代码，根节点到最左NIL：B→R→NIL（黑高=1）

根节点到最右NIL：B→B→NIL（黑高=2）→ 违反规则（实际红黑树不会出现此结构）

黑高的意义是什么？？

我们前面已经了解了，不可能有连续的两个红节点，所以一定是一黑一红，或者两黑。那么通过黑高（Black-Height）的严格一致，将最长路径限制在最短路径的两倍以内，从而保证树高始终维持在O(log n)级别。

这里再给大家放一下红黑树的各种示意图，能对性质有更深的理解。

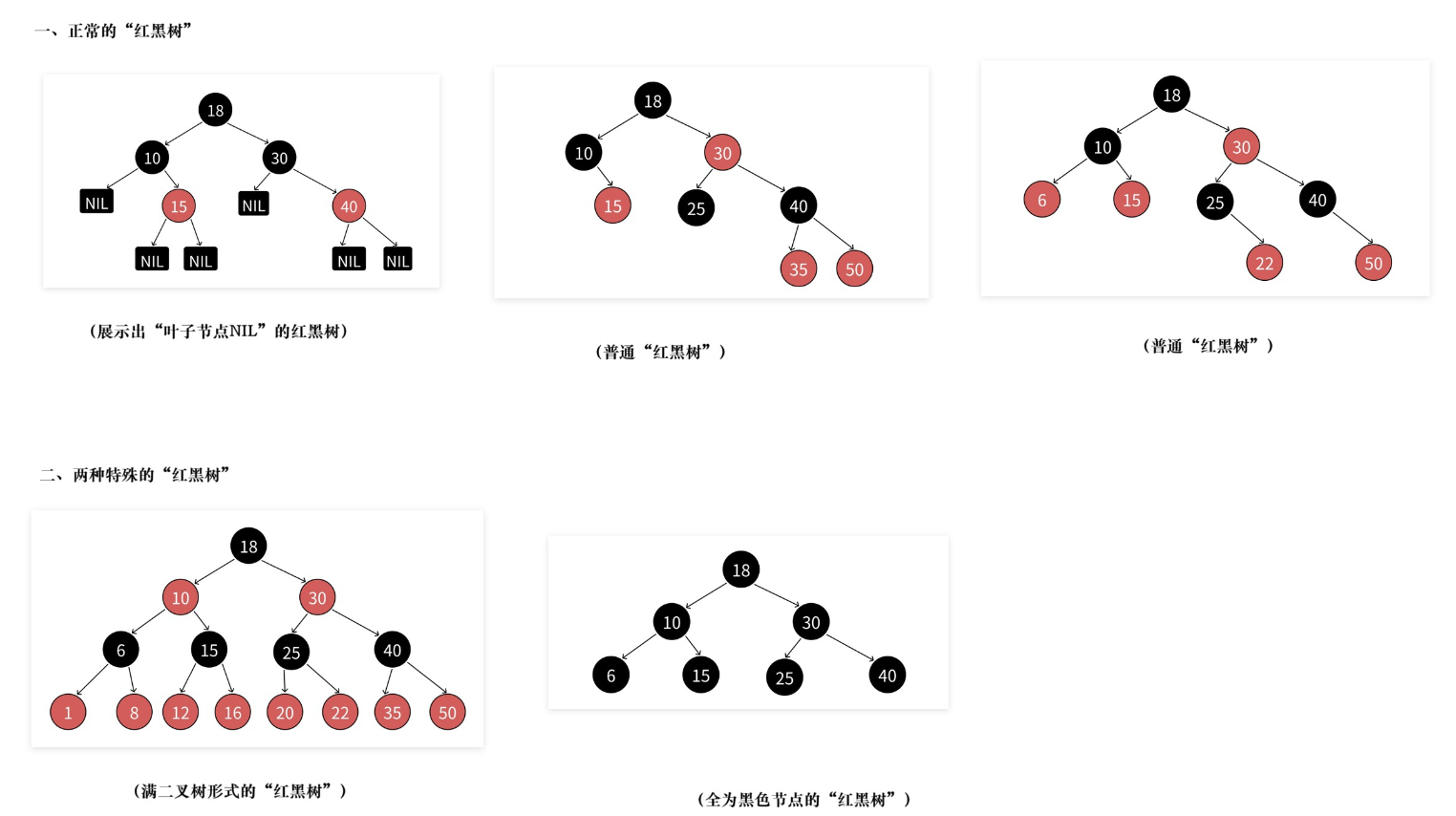
正是黑高的存在，所以满足上面的性质，红黑树就能保证：其最长路径中节点个数不会超过最短路径节点个数的两倍。

三、红黑树实现的总体思路

红黑树包含了之前的AVL树的四大旋转，它没有像AVL树那样严格的平衡，仅要求：最长路径不超过最短路径的两倍即可。但是插入节点是根据大小选择性的走左还是走右，我们是无法控制插入位置的，那么如何保证插入节点后依然属于红黑树？

这里我们提供三板斧：

1.标准BST插入

按照二叉搜索树规则找到插入位置，新节点初始设为红色（最小化对黑高的影响）

设为黑色的代价：必然导致某条路径黑高+1

需要递归调整整棵树的所有路径 平均需O(log n)次调整

设为红色的代价：仅可能产生双红冲突（父节点也是红色）

通过有限的旋转和变色即可修复 平均只需O(1)次调整

2.冲突检测

检测与父节点的冲突。

3.检查修复红黑树

检查黑高的改变有没有影响uncle节点。如有需改变。

四、红黑树的节点结构

// 节点颜色：红或黑
enum Color { RED, BLACK };// 红黑树节点
template<class K, class V>
struct RBTreeNode {// 存储的键值对std::pair<K, V> kv;// 节点指针RBTreeNode* parent;  // 父节点RBTreeNode* left;    // 左孩子RBTreeNode* right;   // 右孩子// 节点颜色Color color;         // 颜色标记// 构造函数RBTreeNode(const std::pair<K, V>& kv): kv(kv),         // 初始化键值对parent(nullptr),// 父节点初始为空left(nullptr),  // 左孩子初始为空right(nullptr), // 右孩子初始为空color(RED)      // 新节点默认红色（符合红黑树规则）{}
};
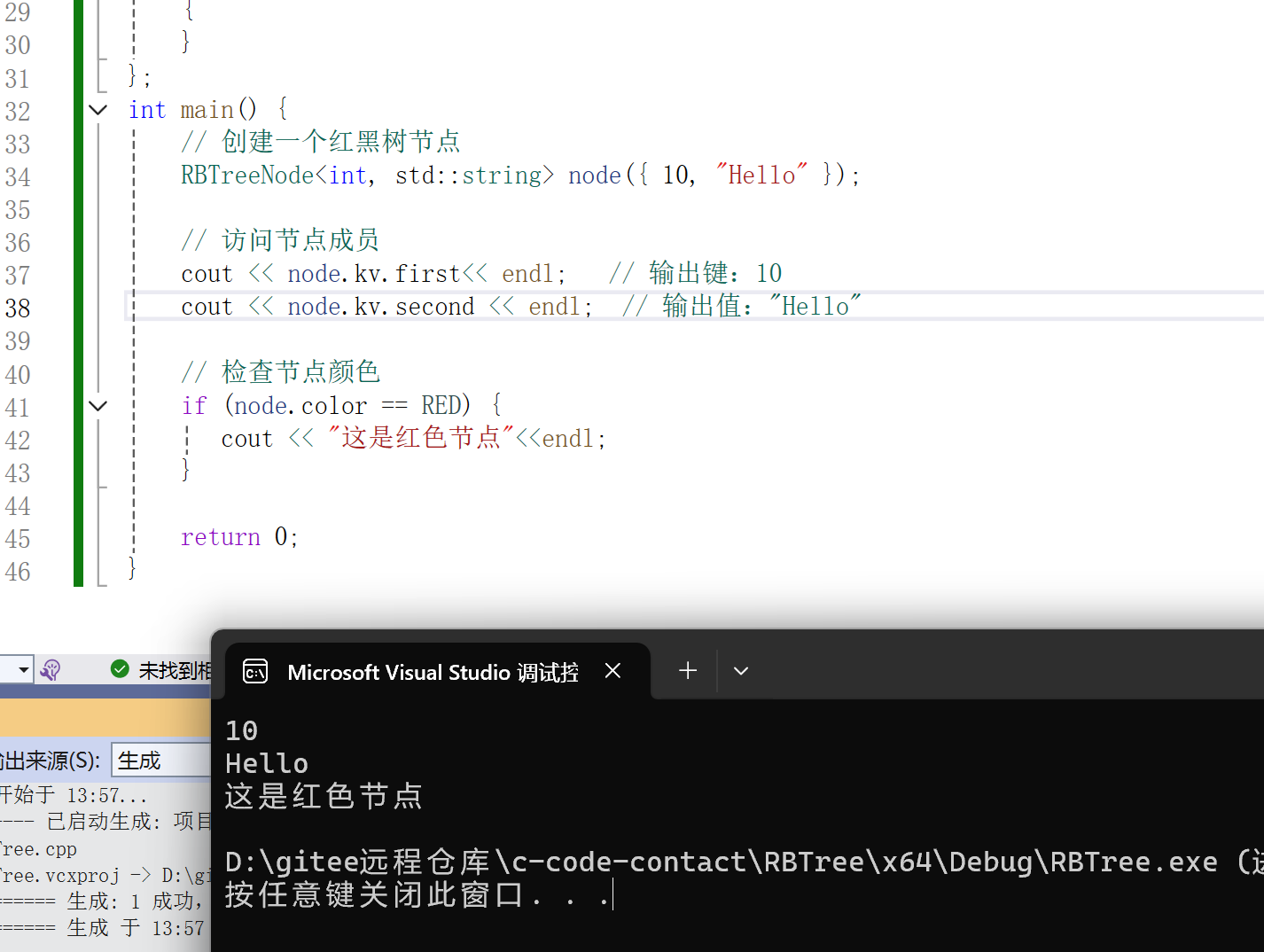
int main() {// 创建一个红黑树节点RBTreeNode<int, std::string> node({10, "Hello"});// 访问节点成员std::cout << node.kv.first;   // 输出键：10std::cout << node.kv.second;  // 输出值："Hello"// 检查节点颜色if(node.color == RED) {std::cout << "这是红色节点";}return 0;
}

五、红黑树的插入操作

首先我们需要先找到那个插入位置：如果是根（颜色为黑）；如果是其它节点（颜色为红）

1.按照二叉搜索的树规则插入新节点

// 插入新节点
bool insert(int key, string value) {// 1. 如果树是空的，直接创建根节点if (root == nullptr) {root = new Node(key, value);root->color = BLACK;  // 根节点必须是黑色return true;}// 2. 寻找插入位置Node* parent = nullptr;Node* current = root;while (current != nullptr) {parent = current;if (key < current->key) {    // 向左找current = current->left;} else if (key > current->key) { // 向右找current = current->right;}else {  // 已经存在相同的keyreturn false; }}// 3. 创建新节点（默认为红色）Node* newNode = new Node(key, value);newNode->parent = parent;  // 连接父节点// 4. 连接到父节点if (key < parent->key) {parent->left = newNode;  // 作为左孩子} else {parent->right = newNode; // 作为右孩子}// 5. 这里应该添加红黑树的平衡调整代码// fixInsert(newNode);return true;
}

2.检测新节点插入后，红黑树的性质是否造到破坏

因为新节点的默认颜色是红色，因此：如果其双亲节点的颜色是黑色，没有违反红黑树任何
性质，则不需要调整；但当新插入节点的双亲节点颜色为红色时，就违反了性质三不能有连
在一起的红色节点，此时需要对红黑树分情况来讨论：

约定:cur为当前节点，p为父节点，g为祖父节点，u为叔叔节点

情况一: cur为红，p为红，g为黑，u存在且为红

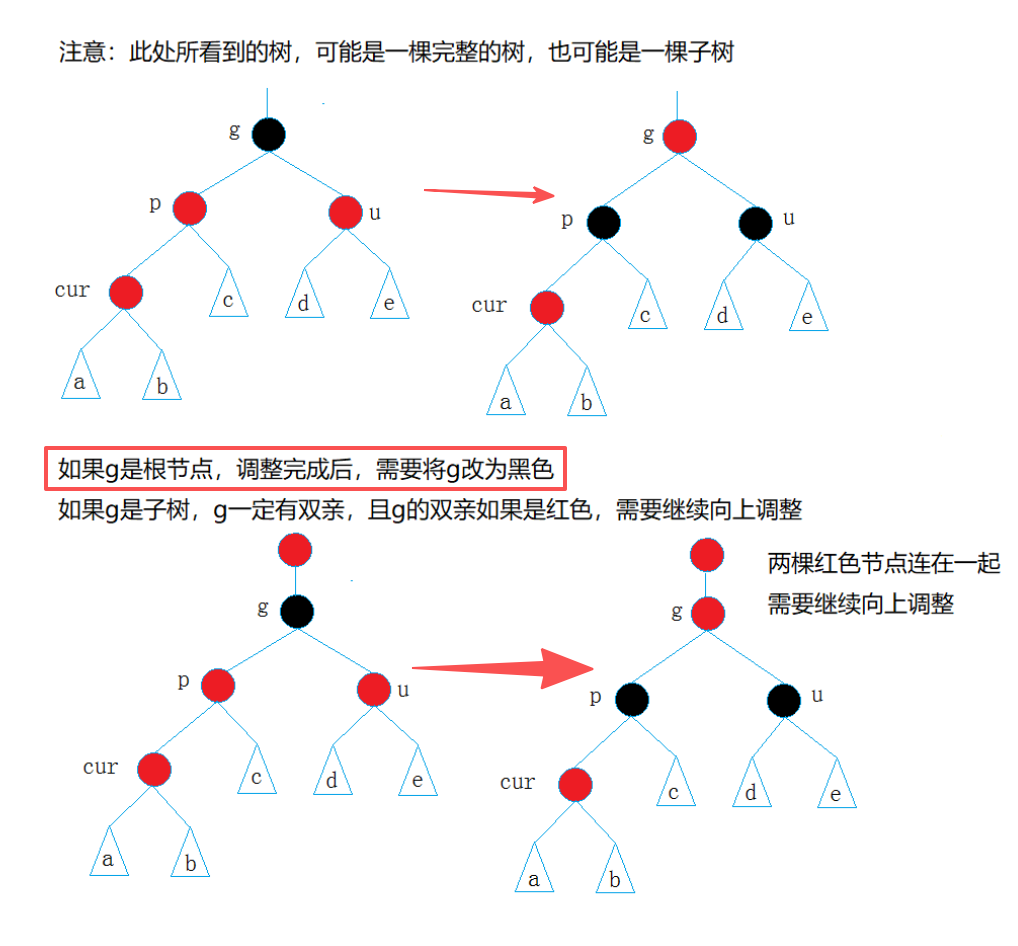
总结，解决方式：将p,u改为黑，g改为红，然后把g当成cur，继续向上调整。

情况二: cur为红，p为红，g为黑，u不存在/u存在且为黑

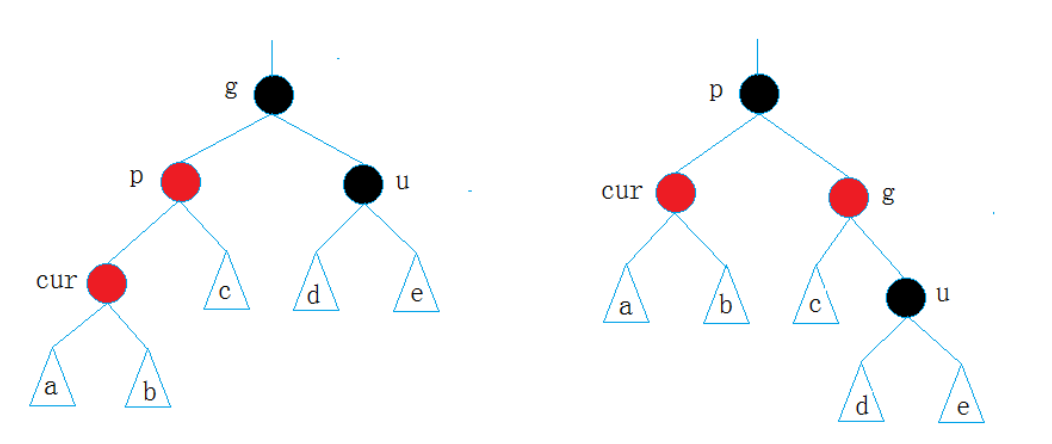
这里我们会发现仅靠变色无法修复，因为会导致黑高不一致。必须通过 旋转 调整树结构，再配合变色。也就是右旋再去判断。

  • p为g的左孩子，cur为p的左孩子，则进行右单旋转；
  • 相反， p为g的右孩子，cur为p的右孩子，则进行左单旋转
  • p、g变色--p变黑，g变红

拓展说明：u的情况有两种
1.如果u节点不存在，则cur一定是新插入节点，因为如果cur不是新插入节点，
则cur和p一定有一个节点的颜色是黑色，就不满足性质4：每条路径黑色节点个
数相同。
2.如果u节点存在，则其一定是黑色的，那么cur节点原来的颜色一定是黑色的，
现在看到其是红色的原因是因为cur的子树在调整的过程中将cur节点的颜色由
黑色改成红色。

🔍 为什么u不存在时cur一定是新插入节点？

      黑(g)/     \红(p)    NIL(黑)/  红(cur)  ← 新插入节点

如果cur不是新插入的节点，而u是NIL（黑色），那么从祖父节点g出发：

路径1：g → p → cur → NIL

路径2：g → u（NIL）

路径1的黑高：g(1) → p(不算) → cur(不算) → NIL(1) → 总计：2

路径2的黑高：g(1) → NIL(1) → 总计：2

如果cur原本就存在且为黑色：

    黑(g)/     \红(p)    NIL(黑)/  黑(cur)  ← 违反性质4！

路径1黑高：g(1) → p(不算) → cur(1) → NIL(1) → 总计：3
路径2黑高：g(1) → NIL(1) → 总计：2

所以不可能，结论：只有当cur是新插入节点时，才可能遇到u不存在的情况

🔍 为什么cur"原来的颜色"是黑色？
这里的"原来"指的是在插入新节点前的状态。考虑红黑树的性质：

每次插入新节点时都设为红色（初始红色）
如果cur不是新插入节点，那么它之前一定是黑色节点被改为红色，这就说明，u存在的时候，一定是自下而上调整成为黑色的。

情况三: cur为红，p为红，g为黑，u不存在/u存在且为黑

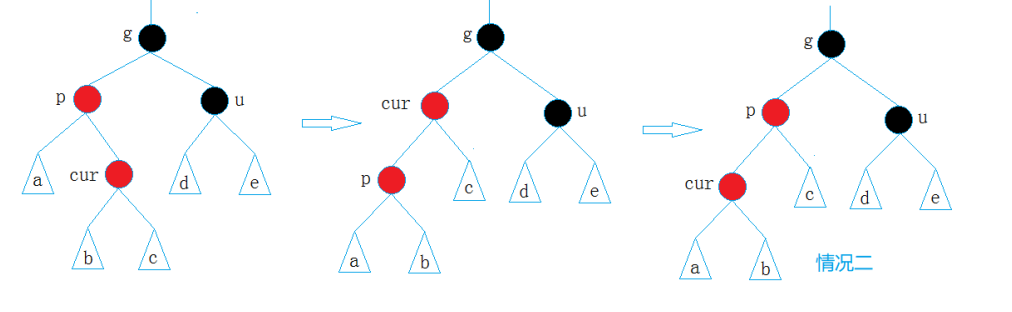
p为g的左孩子，cur为p的右孩子，则针对p做左单旋转；相反， p为g的右孩子，cur为p的左孩子，则针对p做右单旋转即可

六、红黑树的验证

我们来根据下面几个性质检测红黑树：

  1. 根节点是否为黑色
  2. 是否有连续的红色节点
  3. 根据任意一条路径的黑色节点去测一棵树的黑高，看是否相等

总代码

#include <iostream>
#include <utility>
using namespace std;// 节点颜色：红或黑
enum Color { RED, BLACK };// 红黑树节点
template<class K, class V>
struct RBTreeNode {// 存储的键值对pair<K, V> kv;// 节点指针RBTreeNode* parent;  // 父节点RBTreeNode* left;    // 左孩子RBTreeNode* right;   // 右孩子// 节点颜色Color color;         // 颜色标记// 构造函数RBTreeNode(const pair<K, V>& kv): kv(kv),         // 初始化键值对parent(nullptr),  // 父节点初始为空left(nullptr),    // 左孩子初始为空right(nullptr),   // 右孩子初始为空color(RED)        // 新节点默认红色（符合红黑树规则）{}
};// 红黑树类
template<class K, class V>
class RBTree {
public:typedef RBTreeNode<K, V> Node;Node* root = nullptr;// 插入键值对bool insert(const K& key, const V& value) {// 1. 如果树是空的，直接创建根节点if (root == nullptr) {root = new Node(make_pair(key, value));root->color = BLACK;  // 根节点必须是黑色return true;}// 2. 寻找插入位置Node* parent = nullptr;Node* current = root;while (current != nullptr) {parent = current;if (key < current->kv.first) {    // 向左找current = current->left;}else if (key > current->kv.first) { // 向右找current = current->right;}else {  // 已经存在相同的keyreturn false;}}// 3. 创建新节点（默认为红色）Node* newNode = new Node(make_pair(key, value));newNode->parent = parent;  // 连接父节点// 4. 连接到父节点if (key < parent->kv.first) {parent->left = newNode;  // 作为左孩子}else {parent->right = newNode; // 作为右孩子}// 5. 平衡调整fixInsert(newNode);return true;}// 左旋void rotateLeft(Node* x) {Node* y = x->right;x->right = y->left;if (y->left != nullptr) {y->left->parent = x;}y->parent = x->parent;if (x->parent == nullptr) {root = y;} else if (x == x->parent->left) {x->parent->left = y;} else {x->parent->right = y;}y->left = x;x->parent = y;}// 右旋void rotateRight(Node* y) {Node* x = y->left;y->left = x->right;if (x->right != nullptr) {x->right->parent = y;}x->parent = y->parent;if (y->parent == nullptr) {root = x;} else if (y == y->parent->left) {y->parent->left = x;} else {y->parent->right = x;}x->right = y;y->parent = x;}// 插入后修复红黑树性质void fixInsert(Node* z) {while (z != root && z->parent->color == RED) {if (z->parent == z->parent->parent->left) {Node* y = z->parent->parent->right;if (y != nullptr && y->color == RED) {// 情况1：叔叔是红色z->parent->color = BLACK;y->color = BLACK;z->parent->parent->color = RED;z = z->parent->parent;} else {if (z == z->parent->right) {// 情况2：叔叔是黑色，z是右孩子z = z->parent;rotateLeft(z);}// 情况3：叔叔是黑色，z是左孩子z->parent->color = BLACK;z->parent->parent->color = RED;rotateRight(z->parent->parent);}} else {Node* y = z->parent->parent->left;if (y != nullptr && y->color == RED) {// 情况1镜像z->parent->color = BLACK;y->color = BLACK;z->parent->parent->color = RED;z = z->parent->parent;} else {if (z == z->parent->left) {// 情况2镜像z = z->parent;rotateRight(z);}// 情况3镜像z->parent->color = BLACK;z->parent->parent->color = RED;rotateLeft(z->parent->parent);}}}root->color = BLACK;}// 中序遍历打印树void inorderTraversal(Node* node) {if (node == nullptr) return;inorderTraversal(node->left);cout << node->kv.first << "(" << (node->color == RED ? "R" : "B") << ") ";inorderTraversal(node->right);}// 打印树结构void printTree() {inorderTraversal(root);cout << endl;}
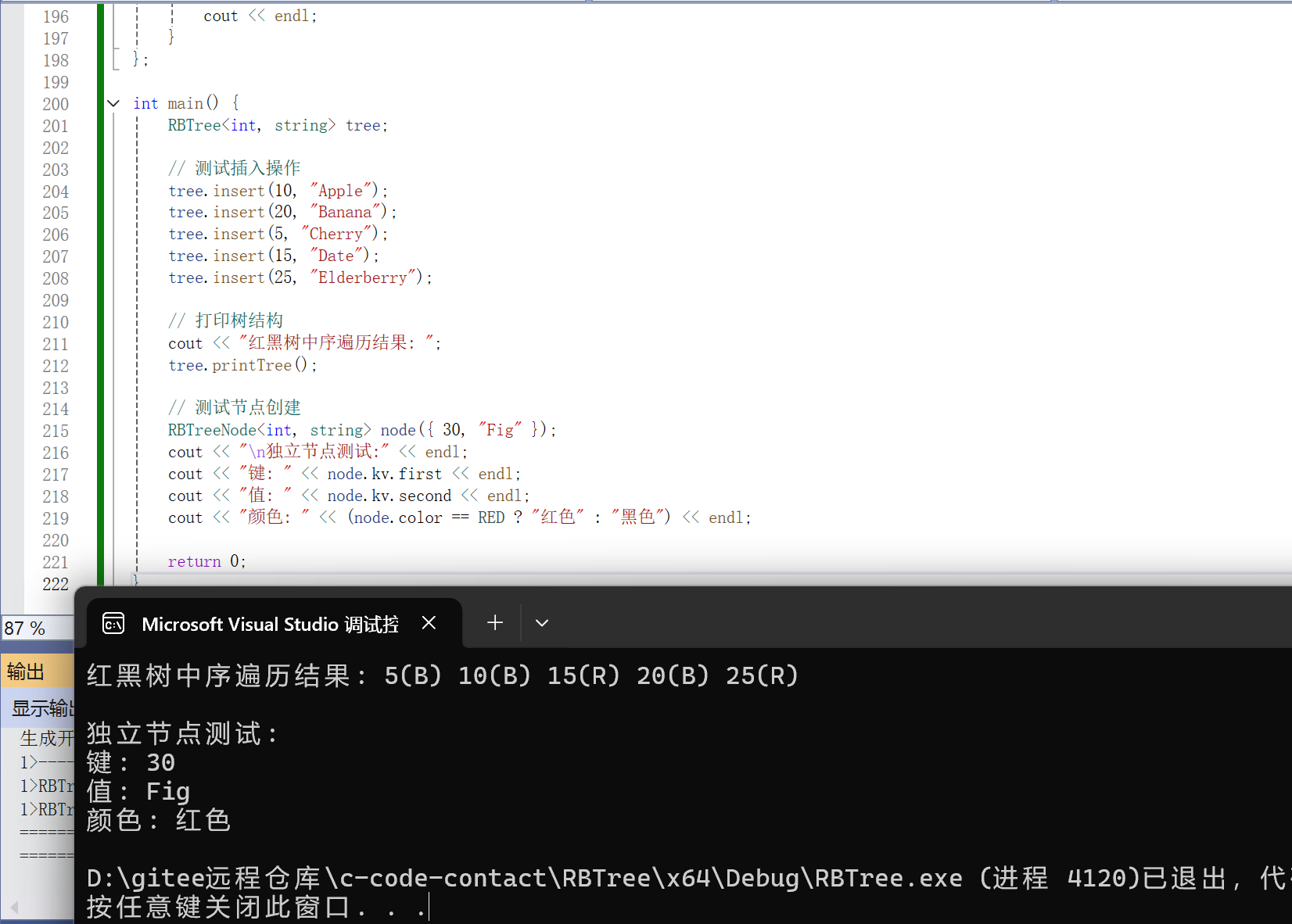
};int main() {RBTree<int, string> tree;// 测试插入操作tree.insert(10, "Apple");tree.insert(20, "Banana");tree.insert(5, "Cherry");tree.insert(15, "Date");tree.insert(25, "Elderberry");// 打印树结构cout << "红黑树中序遍历结果: ";tree.printTree();// 测试节点创建RBTreeNode<int, string> node({30, "Fig"});cout << "\n独立节点测试:" << endl;cout << "键: " << node.kv.first << endl;cout << "值: " << node.kv.second << endl;cout << "颜色: " << (node.color == RED ? "红色" : "黑色") << endl;return 0;
}

http://www.dtcms.com/a/498876.html

相关文章：

  • 将iOS/macOS应用上架至App Store
  • 海南做网站电话如今做哪个网站能致富
  • 数据结构——栈在递归中的应用
  • java.net 包详解
  • Three.js光照技术详解：为3D场景注入灵魂
  • 企业门户网站系统下载网店平台
  • 监听指定事件然后触发鼠标点击操作等，智能文本识别按键工具的使用教程
  • connect 的断线重连
  • wp-config.php文件是什么
  • 编译esp-idf小智报错
  • 微信小程序开发踩坑记：从AI工具翻车到找到合适方案
  • 《3D植被建模痛点解决：开放世界层级实例化+GPU批处理优化方案》
  • openharmony之分布式蓝牙实现多功能场景设备协同实战
  • Linux ARM 程序启动全链路解析：从 shell 到 main（含动态/静态链接）
  • 具身智能黑客松之旅002
  • 免费发布产品网站网站权重能带来什么作用
  • 碰一碰发视频 系统源码 /PHP 语言开发方案
  • 网站大学报名官网入口网站插件代码下载
  • Cors能干什么？为什么需要它？
  • 远程办公自由:rdesktop+cpolar让Windows桌面随身而行
  • 计算机网络（tcp_socket ）
  • 【小白笔记】在编程中，如何将概念上的数据结构（比如“树”）转化为代码中具体的数据类型和对象
  • 【STM32项目开源】STM32单片机智能农业大棚控制系统
  • github开源笔记应用程序项目推荐-Joplin
  • 【Swift】LeetCode 438. 找到字符串中所有字母异位词
  • 【SoC】【W800】基于WM IoT SDK的环境搭建
  • BFS 与 DFS——力扣102.二叉树的层序遍历
  • 使用IOT-Tree的OPC UA Client连接器对接OPC UA Server获取数据到系统中
  • 优质网站建设在哪里wordpress分类目录名称
  • 专题一 之 【双指针】