学习笔记3-深度学习之logistic回归向量化
消除显式循环的方法——向量化,又快又优美!

向量化(Vectorization)指用矩阵/向量运算替代显式的 for 循环,使计算由底层高效的线性代数库(如 BLAS、LAPACK)批量完成。其优势包括:极大加速计算、代码简洁优雅、便于扩展与调试。
实例演示: 当使用 for 循环时,耗时约为 35ms。
import numpy as np
import timea = np.random.rand(100000)
b = np.random.rand(100000)tic = time.time()
c = 0.0
for i in range(100000): # 为公平起见,从 0 到 99999c += a[i] * b[i]
toc = time.time()print(c)
print("For loop: " + str(1000 * (toc - tic)) + " ms")
示例输出(不同机器会有差异):
24985.226970335072
For loop: 34.96 ms
当使用向量化时,耗时约为 0.23ms,计算结果相同,但耗时相差百倍以上。
tic = time.time()
c = np.dot(a, b)
toc = time.time()print(c)
print("Vectorized version: " + str(1000 * (toc - tic)) + " ms")
示例输出:
24985.241649180934
Vectorized version: 0.23 ms
说明:NumPy 在底层调用了 C/Fortran 实现的矩阵运算,避免了 Python 层循环的解释器开销,因此显著加速。
Logistic 上的向量化
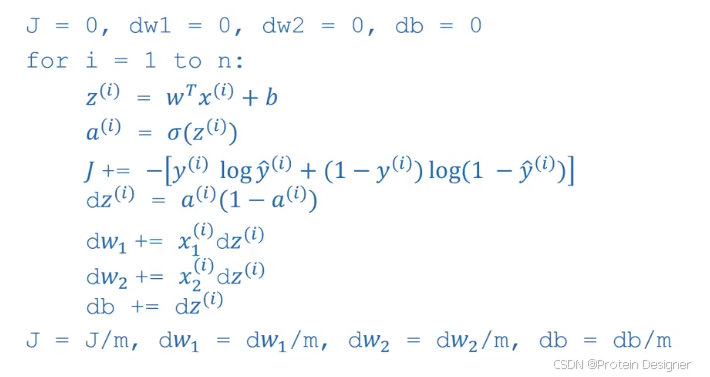
我们来一步一步对上述伪代码进行向量化。首先是输出预测值 A 的向量化。
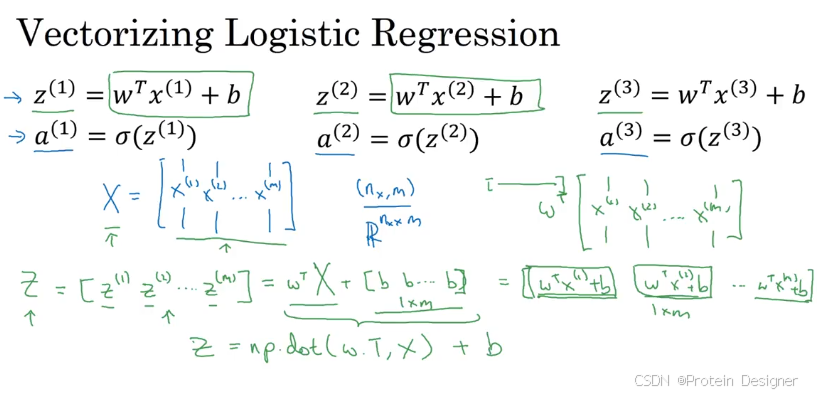
一行代码可生成(只需要加 b 一个标量即可,广播机制)
数学形式(单样本):
z = w ⊤ x + b , a = σ ( z ) , σ ( z ) = 1 1 + e − z . z = w^\top x + b,\qquad a = \sigma(z),\qquad \sigma(z) = \frac{1}{1 + e^{-z}}. z=w⊤x+b,a=σ(z),σ(z)=1+e−z1.
批量形式( m m m 个样本, X ∈ R n × m X\in\mathbb{R}^{n\times m} X∈Rn×m, W ∈ R n × 1 W\in\mathbb{R}^{n\times 1} W∈Rn×1):
Z = W ⊤ X + b ⋅ 1 1 × m , A = σ ( Z ) . Z = W^\top X + b\cdot \mathbf{1}_{1\times m},\qquad A = \sigma(Z). Z=W⊤X+b⋅11×m,A=σ(Z).
示例代码:
def sigmoid(z):return 1.0 / (1.0 + np.exp(-z))# X: (n, m), W: (n, 1), b: scalar
Z = np.dot(W.T, X) + b # 形状: (1, m),b 通过广播加到每一列
A = sigmoid(Z) # 形状: (1, m)
梯度下降法的向量化
三个参数的导数分别为
d w 1 = x 1 ⋅ d z = x 1 ( a − y ) dw_1 = x_1\cdot dz = x_1(a-y) dw1=x1⋅dz=x1(a−y)
d w 2 = x 2 ⋅ d z = x 2 ( a − y ) dw_2 = x_2\cdot dz = x_2(a-y) dw2=x2⋅dz=x2(a−y)
d b = d z = ( a − y ) db = dz = (a-y) db=dz=(a−y)梯度下降法即为:
w 1 : = w 1 − α d w 1 w_1 := w_1 - \alpha\, dw_1 w1:=w1−αdw1
w 2 : = w 2 − α d w 2 w_2 := w_2 - \alpha\, dw_2 w2:=w2−αdw2
b : = b − α d b b := b - \alpha\, db b:=b−αdb
如何对梯度下降法进行向量化?

其中, d z dz dz 可以做如下变换(批量):
d Z = A − Y ∈ R 1 × m . dZ = A - Y\in\mathbb{R}^{1\times m}. dZ=A−Y∈R1×m.
对于 d w dw dw 和 d b db db,我们希望得到如下形式的结果,以去掉第二个 for 循环。
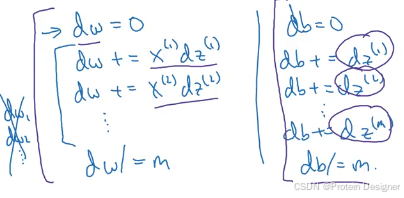
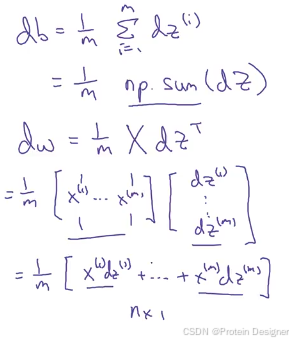
矩阵形式( X ∈ R n × m X\in\mathbb{R}^{n\times m} X∈Rn×m):
d W = 1 m X d Z ⊤ ∈ R n × 1 , d b = 1 m ∑ i = 1 m d Z ( i ) = 1 m 1 1 × m d Z ⊤ ∈ R . dW = \frac{1}{m} X\, dZ^\top \in \mathbb{R}^{n\times 1},\qquad db = \frac{1}{m}\sum_{i=1}^m dZ^{(i)} = \frac{1}{m}\,\mathbf{1}_{1\times m} dZ^\top\in \mathbb{R}. dW=m1XdZ⊤∈Rn×1,db=m1i=1∑mdZ(i)=m111×mdZ⊤∈R.
因此在代码中,我们可以进行梯度下降的向量化(注意是矩阵乘法而非逐元素乘法):
m = X.shape[1]
dZ = A - Y # (1, m)
db = (1.0 / m) * np.sum(dZ) # 标量
dW = (1.0 / m) * np.dot(X, dZ.T) # (n, 1)
最后总结一下,之前的伪代码可以转换成如下格式(此处 A, Z, W, Y 均为向量/矩阵, α \alpha α 为学习率),仅去掉第二个 for 循环,时间复杂度显著下降,同时第一个 for 循环(迭代轮次)通常保留。
# 假设已给出:X (n, m), Y (1, m), 初始化 W (n, 1), b (scalar), 学习率 alpha
num_iters = 1000
for iter in range(num_iters):# 前向传播Z = np.dot(W.T, X) + b # (1, m)A = sigmoid(Z) # (1, m)# 反向传播dZ = A - Y # (1, m)db = (1.0 / X.shape[1]) * np.sum(dZ) # scalardW = (1.0 / X.shape[1]) * np.dot(X, dZ.T) # (n, 1)# 梯度下降更新参数W = W - alpha * dWb = b - alpha * db
tips:
-
广播机制 参考:NumPy 广播机制
-
NumPy vector 技巧 —— 不要使用形状为
(5,)或(n,)这种秩为 1 的数组
# 如果不指定,生成的仅为一个秩为 1 的数组而非矩阵
a = np.random.randn(5)
# 例如: [ 1.21177442 -0.27537481 -0.21272904 -0.18874844 0.59819099]# 显式生成矩阵,生成 (5, 1) 列向量(推荐)
a = np.random.randn(5, 1)
assert a.shape == (5, 1)
# [[ 1.03824448],
# [-0.21599562],
# [ 0.04871433],
# [ 1.50486642],
# [ 1.086666 ]]
- 随意插入assert以保证形状一致,便于调试:
assert W.shape == (n, 1)
assert X.shape == (n, m)
assert Y.shape == (1, m)
- 数值稳定性与实现细节(可选但推荐)
- 对 A 做裁剪避免 log ( 0 ) \log(0) log(0):如
A = np.clip(A, 1e-15, 1-1e-15) - 使用
@或np.dot做矩阵乘法,避免用*逐元素乘法替代矩阵乘法 b保持为标量(或形状(1,1)),便于广播
- loss function 的证明(强烈建议去听老师的课程—logistic损失函数的解释,讲的非常清楚)
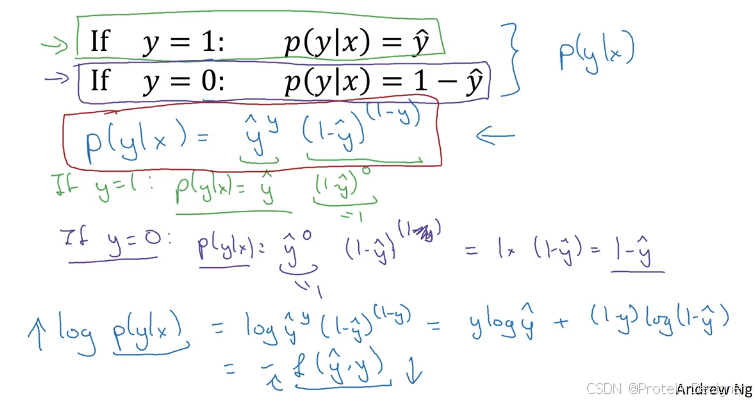
从极大似然出发:对于二分类样本 ( x ( i ) , y ( i ) ) (x^{(i)}, y^{(i)}) (x(i),y(i)),其中 y ( i ) ∈ { 0 , 1 } y^{(i)}\in\{0,1\} y(i)∈{0,1},模型输出
a ( i ) = P ( Y = 1 ∣ x ( i ) ) = σ ( w ⊤ x ( i ) + b ) . a^{(i)} = P(Y=1\mid x^{(i)}) = \sigma(w^\top x^{(i)} + b). a(i)=P(Y=1∣x(i))=σ(w⊤x(i)+b).
条件似然:
p ( y ( i ) ∣ x ( i ) ; w , b ) = ( a ( i ) ) y ( i ) ( 1 − a ( i ) ) 1 − y ( i ) . p(y^{(i)}\mid x^{(i)};w,b)=\big(a^{(i)}\big)^{y^{(i)}} \big(1-a^{(i)}\big)^{1-y^{(i)}}. p(y(i)∣x(i);w,b)=(a(i))y(i)(1−a(i))1−y(i).
负对数似然(单样本损失)为
L ( a ( i ) , y ( i ) ) = − log p ( y ( i ) ∣ x ( i ) ; w , b ) = − [ y ( i ) log a ( i ) + ( 1 − y ( i ) ) log ( 1 − a ( i ) ) ] . L\big(a^{(i)}, y^{(i)}\big) = -\log p\big(y^{(i)}\mid x^{(i)};w,b\big) = -\Big[y^{(i)}\log a^{(i)} + \big(1 - y^{(i)}\big)\log\big(1 - a^{(i)}\big)\Big]. L(a(i),y(i))=−logp(y(i)∣x(i);w,b)=−[y(i)loga(i)+(1−y(i))log(1−a(i))].
这即为逻辑回归常用的交叉熵损失。其关于 z ( i ) = w ⊤ x ( i ) + b z^{(i)}=w^\top x^{(i)}+b z(i)=w⊤x(i)+b 的导数为
∂ L ∂ z ( i ) = a ( i ) − y ( i ) , \frac{\partial L}{\partial z^{(i)}} = a^{(i)} - y^{(i)}, ∂z(i)∂L=a(i)−y(i),
进而
∂ L ∂ w = ( a ( i ) − y ( i ) ) x ( i ) , ∂ L ∂ b = a ( i ) − y ( i ) . \frac{\partial L}{\partial w} = \big(a^{(i)} - y^{(i)}\big)\, x^{(i)},\qquad \frac{\partial L}{\partial b} = a^{(i)} - y^{(i)}. ∂w∂L=(a(i)−y(i))x(i),∂b∂L=a(i)−y(i).
cost function 的证明
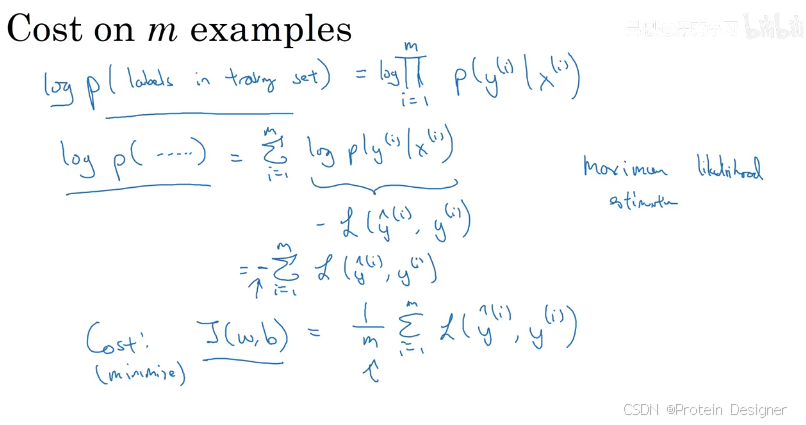
对于 m m m 个样本,代价函数为
J ( w , b ) = 1 m ∑ i = 1 m L ( a ( i ) , y ( i ) ) = − 1 m ∑ i = 1 m [ y ( i ) log a ( i ) + ( 1 − y ( i ) ) log ( 1 − a ( i ) ) ] . J(w,b)=\frac{1}{m}\sum_{i=1}^m L\big(a^{(i)}, y^{(i)}\big) = -\frac{1}{m}\sum_{i=1}^m \Big[y^{(i)}\log a^{(i)} + \big(1-y^{(i)}\big)\log\big(1-a^{(i)}\big)\Big]. J(w,b)=m1i=1∑mL(a(i),y(i))=−m1i=1∑m[y(i)loga(i)+(1−y(i))log(1−a(i))].
将所有样本整合为矩阵形式,令
Z = W ⊤ X + b , A = σ ( Z ) , d Z = A − Y ∈ R 1 × m , Z = W^\top X + b,\quad A=\sigma(Z),\quad dZ = A - Y\in\mathbb{R}^{1\times m}, Z=W⊤X+b,A=σ(Z),dZ=A−Y∈R1×m,
则梯度向量化为
d W = 1 m X d Z ⊤ ∈ R n × 1 , d b = 1 m ∑ i = 1 m d Z ( i ) ∈ R . dW = \frac{1}{m} X\, dZ^\top\in\mathbb{R}^{n\times 1},\qquad db = \frac{1}{m}\sum_{i=1}^m dZ^{(i)}\in\mathbb{R}. dW=m1XdZ⊤∈Rn×1,db=m1i=1∑mdZ(i)∈R.
这与前述逐坐标推导一致,且消除了对样本维度的显式循环。
结语:
向量化的核心是“去掉循环,拥抱矩阵运算”。在 Logistic 回归中,通过将前向与反向传播写成矩阵形式,可以用极少的 Python 代码完成高效训练。这一思想在更复杂的深度学习模型(如全连接网络、卷积网络、RNN)中同样至关重要。
