Cross Product / Vector Product / 向量外积 / 叉积 / 矢量外积 可理解为一个意思

Cross Product / Vector Product / 向量外积 / 叉积 / 矢量外积 可理解为一个意思

向量（Vector）的两个要素
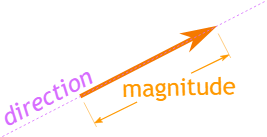
向量是既有大小、又有方向的量，用箭头（长度表大小，指向表方向）
magnitude（大小/模长）：橙色箭头的长度代表向量的“大小”（或“模长”），描述向量的“强度”或“尺度”（比如力的大小、速度的快慢）。
direction（方向）：紫色虚线的延伸指向代表向量的“方向”，描述向量的“指向”（比如力的作用方向、速度的运动方向）。

两个向量可以用 “叉积（法）Cross Product ” 来相乘。

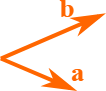
两个向量的叉积 $a\times b$ 是另一个与这两个向量都成直角的向量。

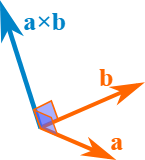
理解

设三维欧几里得空间${\mathbb{R}}^3$中的两个向量$\mathbf{a}=(a_x,a_y,a_z)$与$\mathbf{b}=(b_x,b_y,b_z)$，叉积$\mathbf{a}\times \mathbf{b}$可从几何与代数两个维度理解。

几何理解

叉积$\mathbf{a}\times \mathbf{b}$是一个满足以下条件的向量：
模长：$|\mathbf{a}\times \mathbf{b}|=|\mathbf{a}|\cdot |\mathbf{b}|\sin \theta$，其中$|\mathbf{a}|$、$|\mathbf{b}|$分别为向量$\mathbf{a}$、$\mathbf{b}$的模长，$\theta$为两向量的夹角（取值范围$0\le \theta \le \pi$）。该模长的几何意义是“以$\mathbf{a}$、$\mathbf{b}$为邻边的平行四边形面积”。
方向：与向量$\mathbf{a}$、$\mathbf{b}$均垂直（即垂直于$\mathbf{a}$、$\mathbf{b}$所确定的平面），具体方向由右手定则判断：将右手四指从$\mathbf{a}$沿“小于$180^{\circ }$的最小夹角”弯向$\mathbf{b}$，此时大拇指指向即为$\mathbf{a}\times \mathbf{b}$的方向。

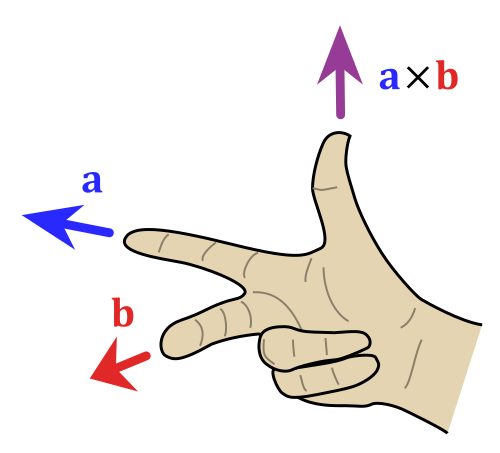
从数学表达式上，叉积的几何定义可写为：
$$\mathbf{a}\times \mathbf{b}=\left(|\mathbf{a}|\cdot |\mathbf{b}|\sin \theta \right)\mathbf{n}$$
其中$\mathbf{n}$是垂直于$\mathbf{a}$、$\mathbf{b}$所在平面的单位向量，方向由右手定则确定。

代数理解（分量展开式）

以$x$轴、$y$轴、$z$轴的单位向量$\mathbf{i}$、$\mathbf{j}$、$\mathbf{k}$为基向量，叉积可通过三阶行列式展开计算，具体形式为：
$$\mathbf{a}\times \mathbf{b}=\left|\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\\ a_x& a_y& a_z\\ b_x& b_y& b_z\end{array}\right|$$

将上述行列式按第一行展开，可得到叉积的分量形式：
$$\mathbf{a}\times \mathbf{b}=(a_y{b}_z-a_z{b}_y)\mathbf{i}-(a_x{b}_z-a_z{b}_x)\mathbf{j}+(a_x{b}_y-a_y{b}_x)\mathbf{k}$$

若以向量的分量坐标直接表示，叉积可简化为：
$$\mathbf{a}\times \mathbf{b}=\left(a_y{b}_z-a_z{b}_y,a_z{b}_x-a_x{b}_z,a_x{b}_y-a_y{b}_x\right)$$

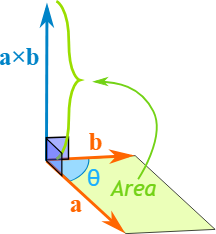
向量所在平面与夹角：浅绿色平面是向量$a$和$b$共同所在的平面，两向量的夹角为$\theta$。
叉积的方向：图中蓝色箭头表示$a\times b$，它垂直于浅绿色平面（即同时与$a$、$b$垂直），体现了叉积“生成与原两向量均垂直的新向量”这一核心特点。
叉积的模长（几何意义）：浅绿色平面上，由$a$、$b$为邻边张成的平行四边形面积（图中标注“Area”的区域），恰好等于叉积的模长$|a\times b|$（对应公式$|a\times b|=|a|\cdot |b|\sin \theta$）。