人工智能的本质是什么

终极目的：

分类（划线分类，划曲线分类）

实现方法：

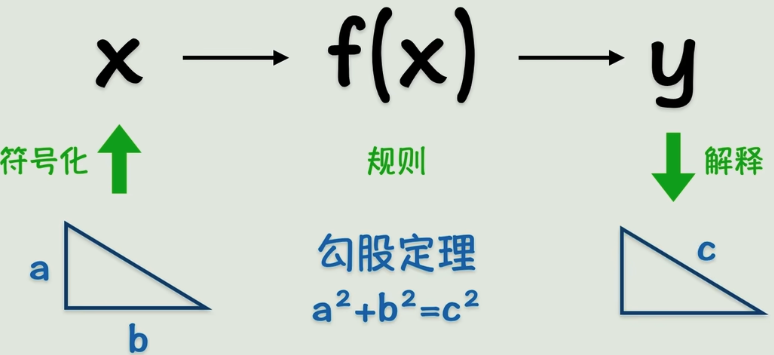
找到一个f(x)，可以符合已知的输入x，和已知的输出y。就是已知很多个输入输出，但是不知道，这些点最终是用一个什么f(x)来表示。

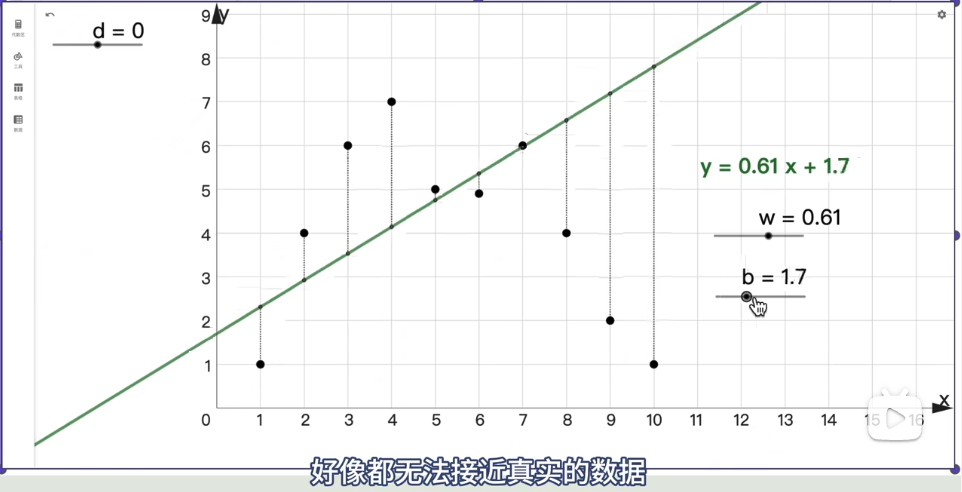
方法1：直线逼近（多次调整系数w(权重），和b（偏移））

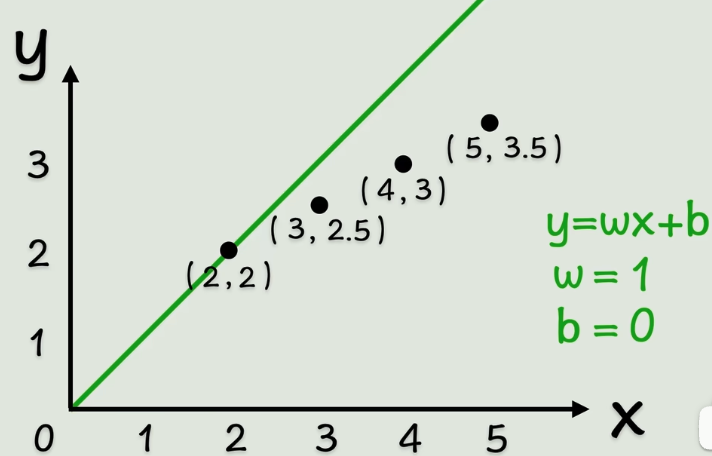最开始从一个最简单的线性函数开始调整

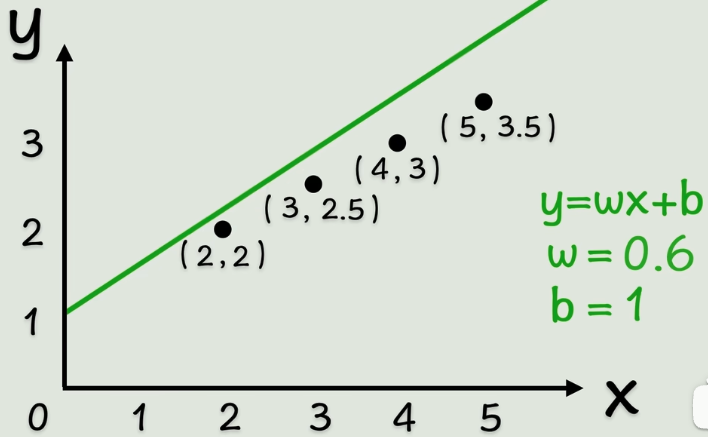
经过多次调整。。。

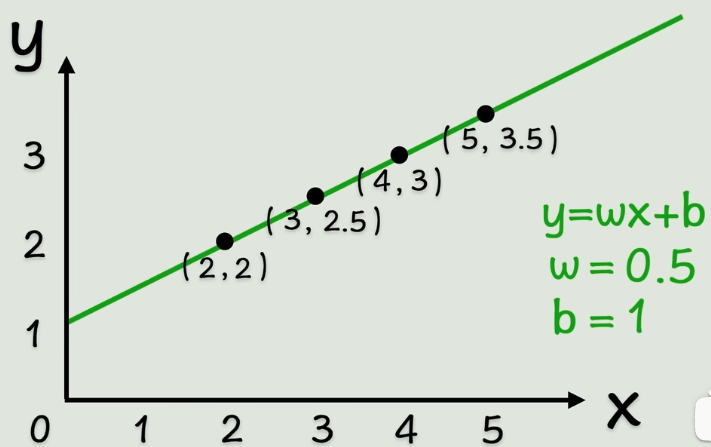完全吻合

有时候如果很难完全吻合呢？多次调整大差不差就行

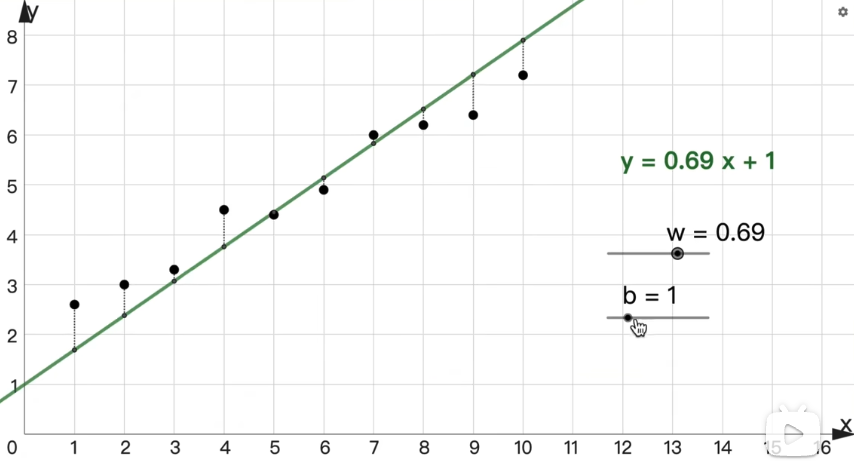
方法2：去求解这个规则

方法3：实在太难了，让电脑自己一步步调整，去逐渐逼近

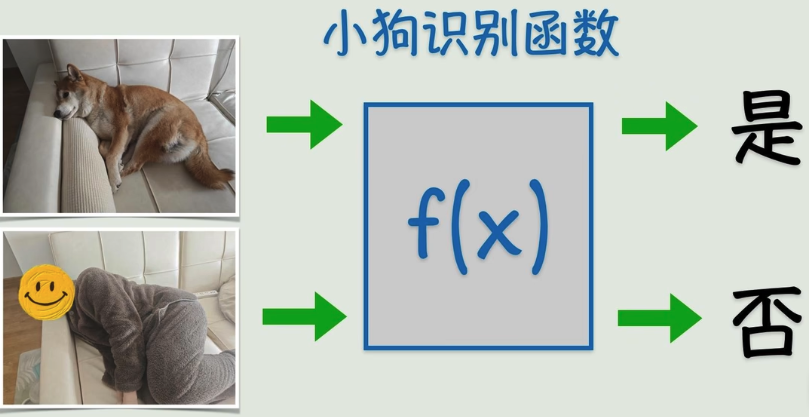
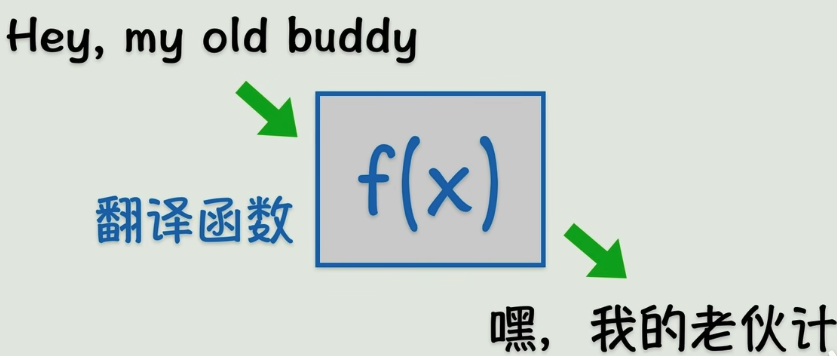
例如，还是同上使用简化，逼近的思想

如果还是不能用直线去拟合分类函数，那就需要这条直线弯一弯了

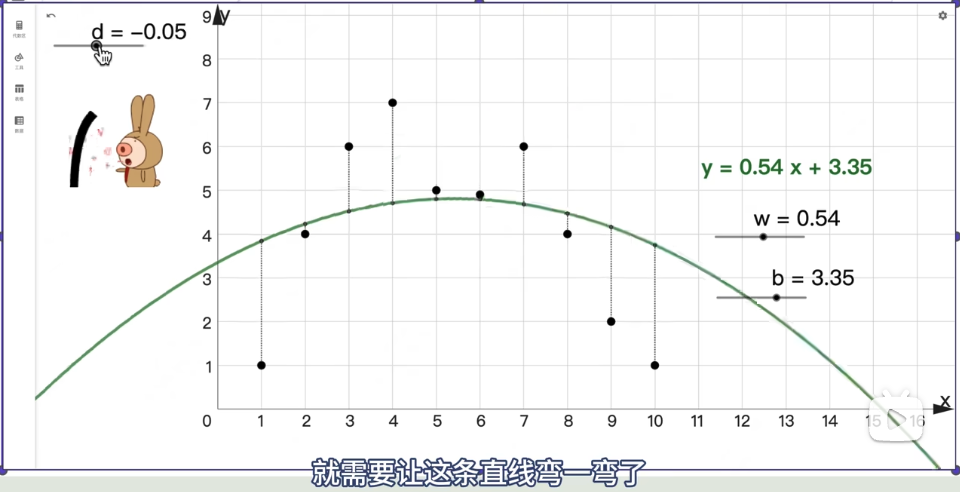
很简单，可以在线性函数外层套一个非线性的激活函数，比如：平方，sin，e，

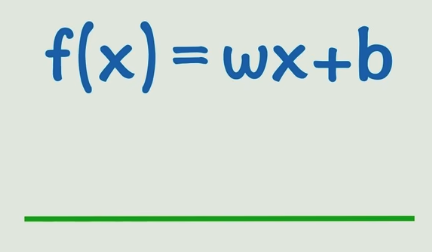
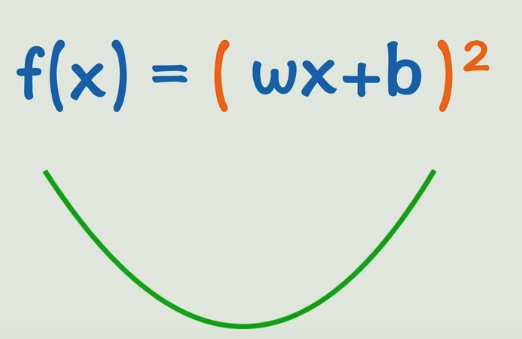
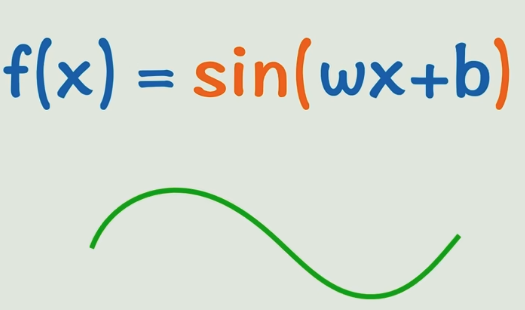
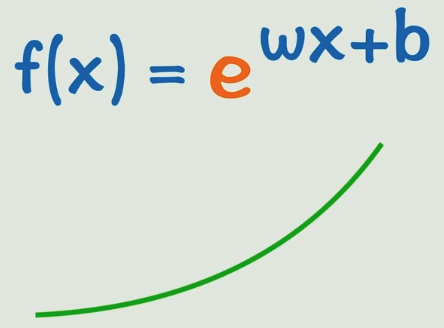
这就是激活函数：它的目的就是把原本死气沉沉的线性关系给盘活了，变成了变化能力更强的非线性关系，大家千万别害怕，常用的激活函数都简单到爆炸（我没觉得），但是就是能起到很好的效果。

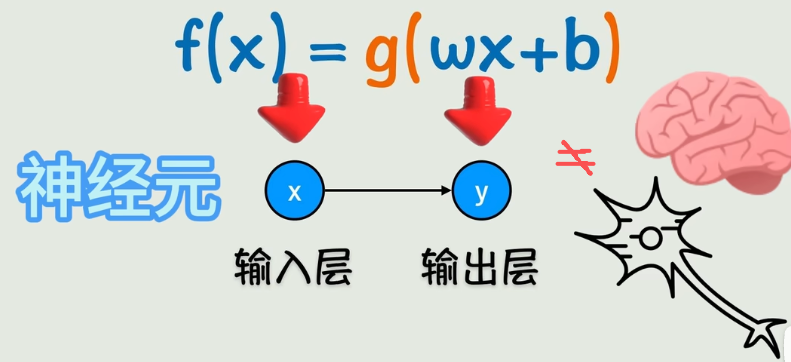
我们最简单的假设是只有一个输入，

但实际中很可能有很多个输入，

如果只套一个激活函数，曲线还是弯的不够灵活，

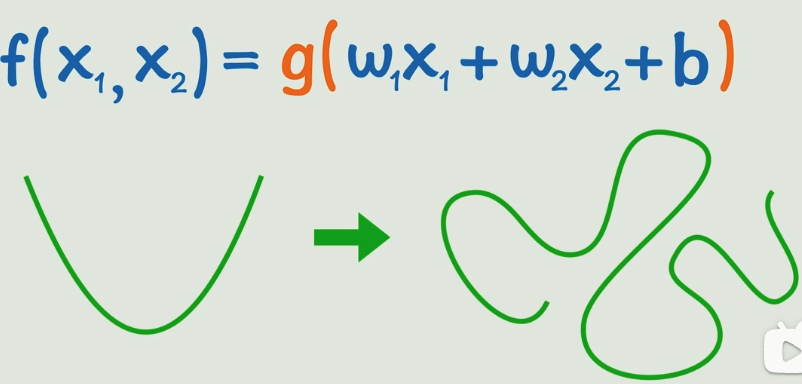
那该怎么办呢？

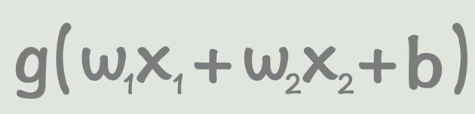
就是把上边这一大坨，加上一个线性变换，然后再加一个激活函数。

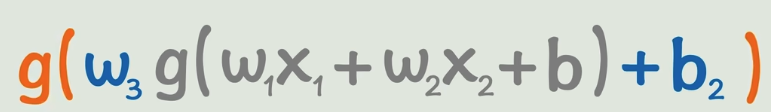
通过这样的方式我们就可以无限套娃下去了，我们就可以构造出非常非常复杂的非线性关系，理论上可以无限逼近任意的函数

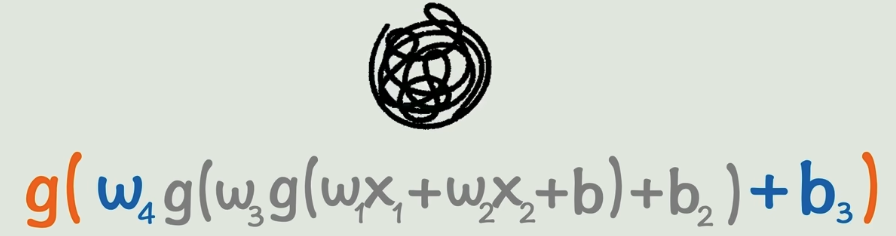
但是这么一大坨，难表示，在这里每个小圈圈叫做一个神经元，在这里我不建议你用生物的神经元和这个类比，因为他两其实一毛钱关系也没有，看似很形象，但实际上返回会影响理解。

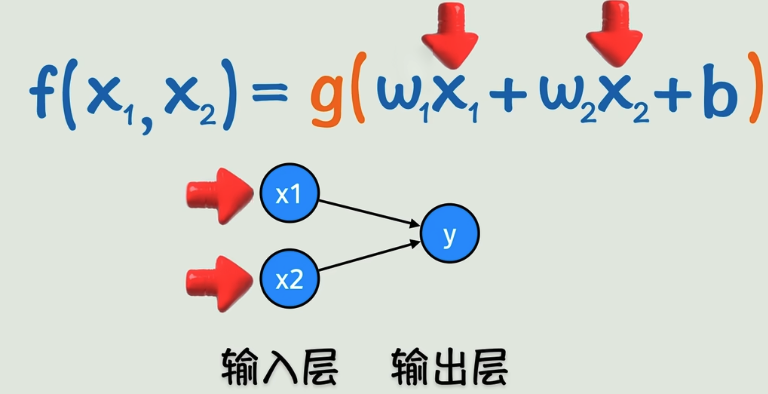
刚刚我们说输入输出可能有多个

每多套一层，横向就会扩展出一层

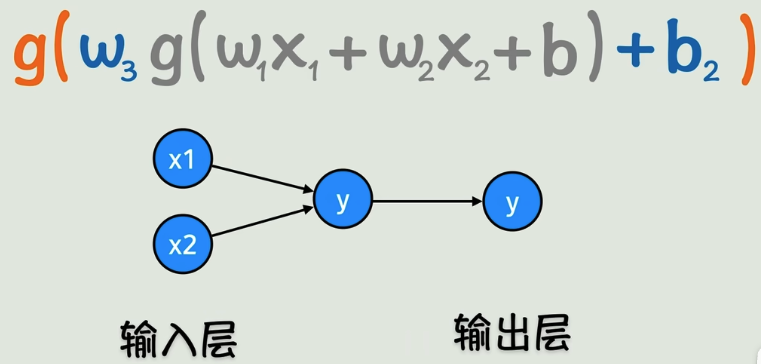
当然中间这层就不再是输出了，而变成了隐藏层，

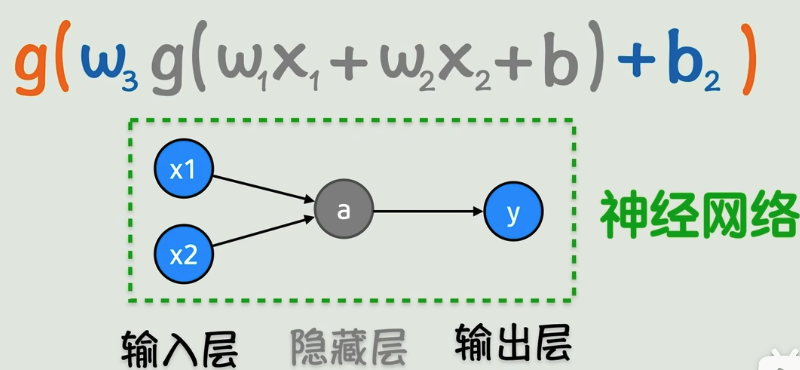
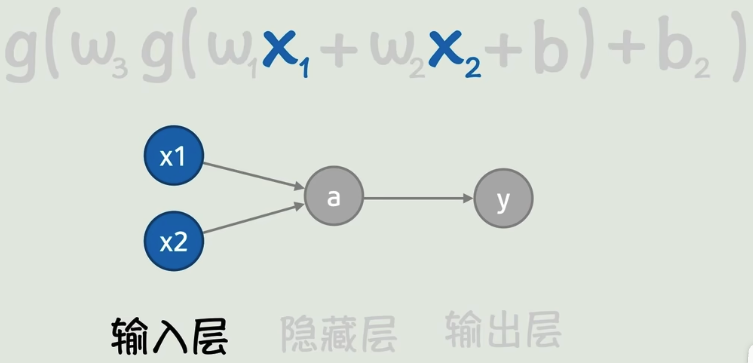
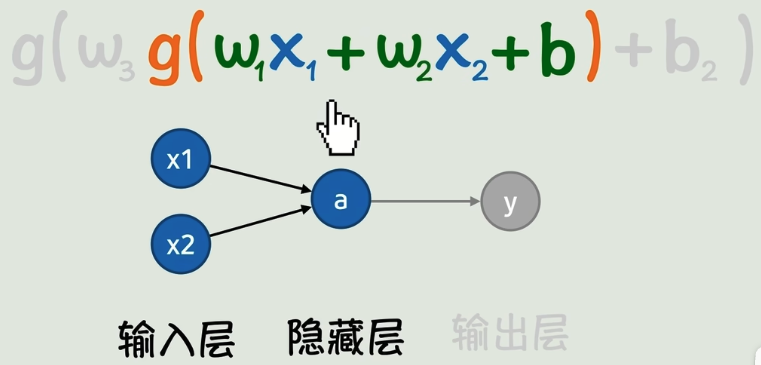
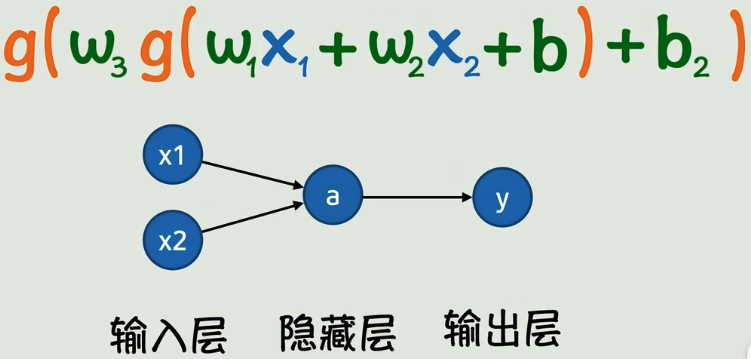
神经网络的每一层都可以无限增加，进而就可以形成非常复杂的曲线

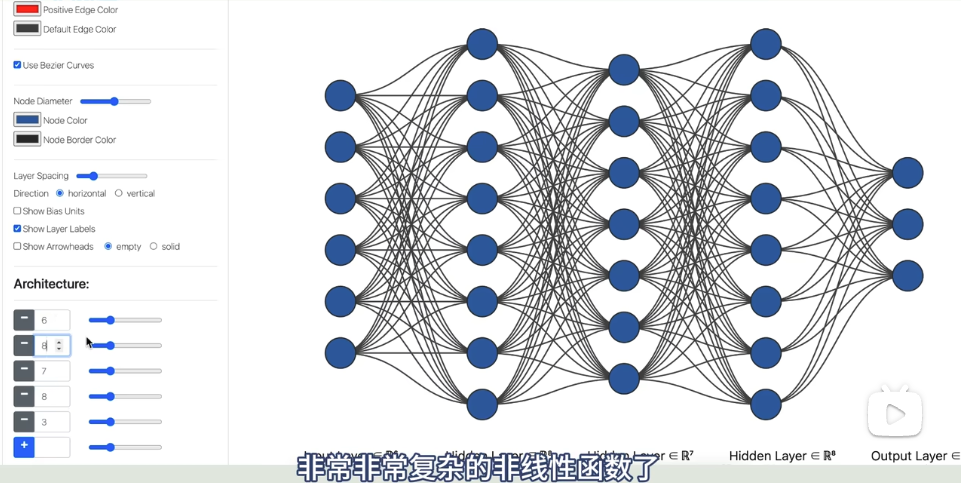
虽然曲线很复杂，但是我们的目的很明确，就是根据已知数据猜出这里的w和b

恭喜你，从函数到神经网的这条路已经被你搞懂了，剩下的所有乱七八糟的知识都仅仅是为了算出这个w和b而已。

内容取自飞天闪客的视频：https://www.bilibili.com/video/BV1NCgVzoEG9?spm_id_from=333.788.videopod.sections&vd_source=e10f137a63ff65947d019d16bb78ea8d