CS50ai: week2 Uncertainty我的笔记B版：一口气从“爬山”到“退火”, 优化与CSP超好懂入门

写给零基础但想快速上手 AI 里“选最优”的你。轻松点儿看，但招儿都很正。

---

前言：为什么你会卡在“小山包”上？

很多 AI 问题的核心不在于“怎么走”，而在于“哪儿最好”。比如：医院建在哪最省路？快递员走哪条环线最短？课程考试怎么排才不撞车？这类优化问题共同点是：从一堆可行方案里挑“最好”的那个。今天我们用一篇小教程，把局部搜索（local search）、模拟退火（simulated annealing）、**线性规划（LP）和约束满足问题（CSP）**串起来，既讲直觉，也给你能落地的伪代码与实战心法。

---

1）局部搜索：只带一个状态就出门的“轻装派”

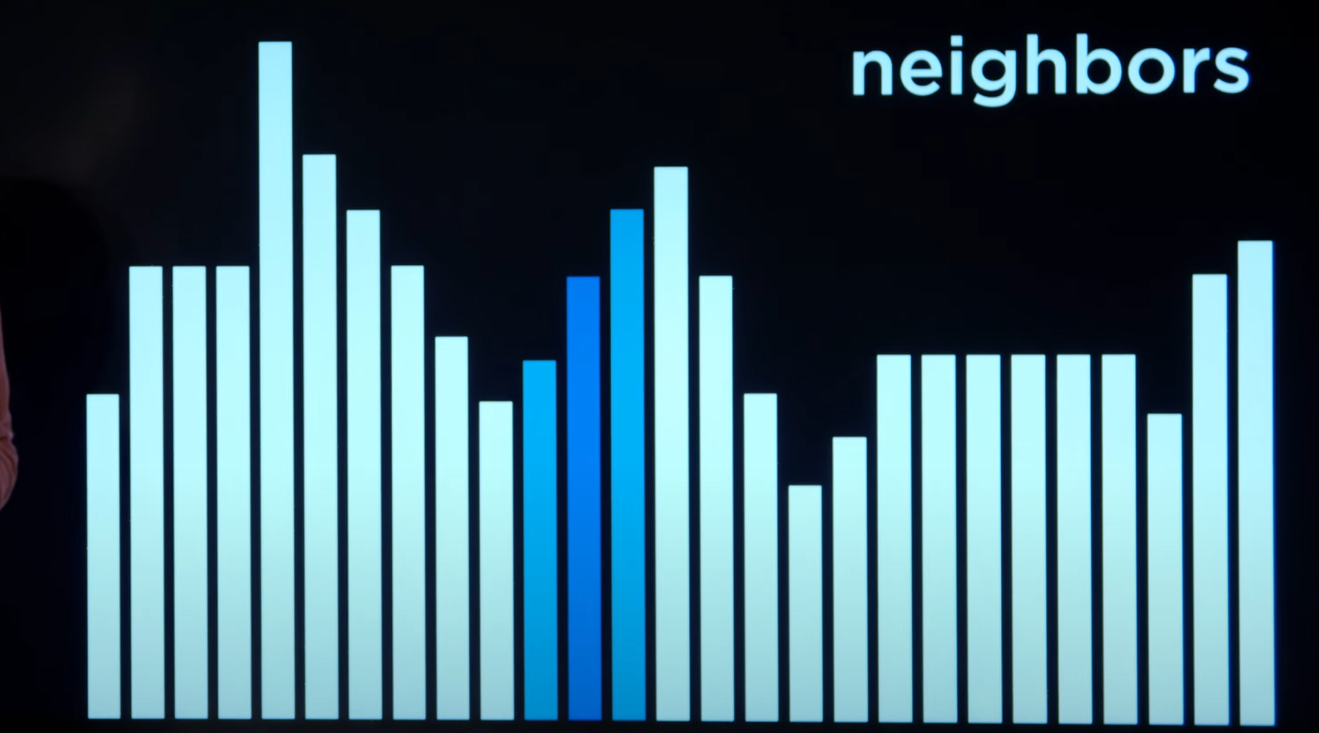
状态空间地形（state-space landscape）

把每个可行状态画成一根柱子，高度 = 目标函数值（要最大化时）或代价函数值（要最小化时）。我们的任务是找到全局最优：最高峰（或最低谷）。局部搜索的做法很“近视眼”——只维护一个当前状态，再在它的邻居里挑更好的，向左一步或向右一步，慢慢爬。

爬山算法（Hill Climbing）

想最大化就每次选更高的邻居；想最小化就每次选更低的邻居；若无更好邻居就停。

HILL-CLIMB(problem):current ← initial_state(problem)   # 随机也行loop:neighbor ← best_neighbor(current)   # 最大化选最高；最小化选最低if value(neighbor) ≤ value(current): return current                  # 没更好就收工current ← neighbor

常见坑

• 局部最优：卡在小山包（local maxima/minima）

• 平台（plateau）：一片平的，不知道往哪走

• 肩部（shoulder）：虽不是最优，但短期内不变好

变体小抄

• 最陡上升：每次选“最最好”的邻居（贪心）

• 随机/首选上升：只要更好就跳，省评估

• 随机重启：换多个随机起点，多跑几次取最好

• 局部束搜索（beam）：同时保留前 k 个最好状态
  这些都在缓解“卡局部最优”的风险。

---

2）模拟退火：允许“变差”才能走到更好

纯爬山永远不往下走，注定可能错过更高峰。**模拟退火（SA）**借鉴物理退火：一开始“温度高”允许偶尔接收更差邻居（以概率），之后温度逐步降低，变得保守。

核心规则（以最大化为例）：

1. 若 ΔE = value(neighbor) − value(current) > 0：必接收

2. 若 ΔE ≤ 0：以概率 exp(ΔE / T) 接收（T 为温度）

SIMULATED-ANNEALING(problem, max_iter):current ← initial_state(problem)for t = 1..max_iter:T ← temperature(t)       # 逐步下降，如 T0 * α^t 或 T0/(1+kt)neighbor ← random_neighbor(current)ΔE ← value(neighbor) - value(current)if ΔE > 0:current ← neighborelse with probability exp(ΔE / T):current ← neighborreturn current

什么时候用？

• 地形“坑坑洼洼”局部最优多：如**旅行商问题（TSP）**用“2-opt”邻域（交换两条边）常配 SA 作为近似法。

---

3）线性规划（LP）：当目标和约束都“线性”

问题形态
最小化 c^T x，满足

• 线性不等式：Ax ≤ b（或等式 A_eq x = b_eq）

• 变量界：ℓ ≤ x ≤ u

例子：两台机器 x1/x2，费用最小；受限于劳动力和产出需求。能用 SciPy linprog 一步搞定（算法底层常用单纯形或内点法）。当你的目标/约束都是线性的，优先考虑 LP——它是有“成熟工业级解法”的。

---

4）约束满足问题（CSP）：变量、取值与“不许这样”

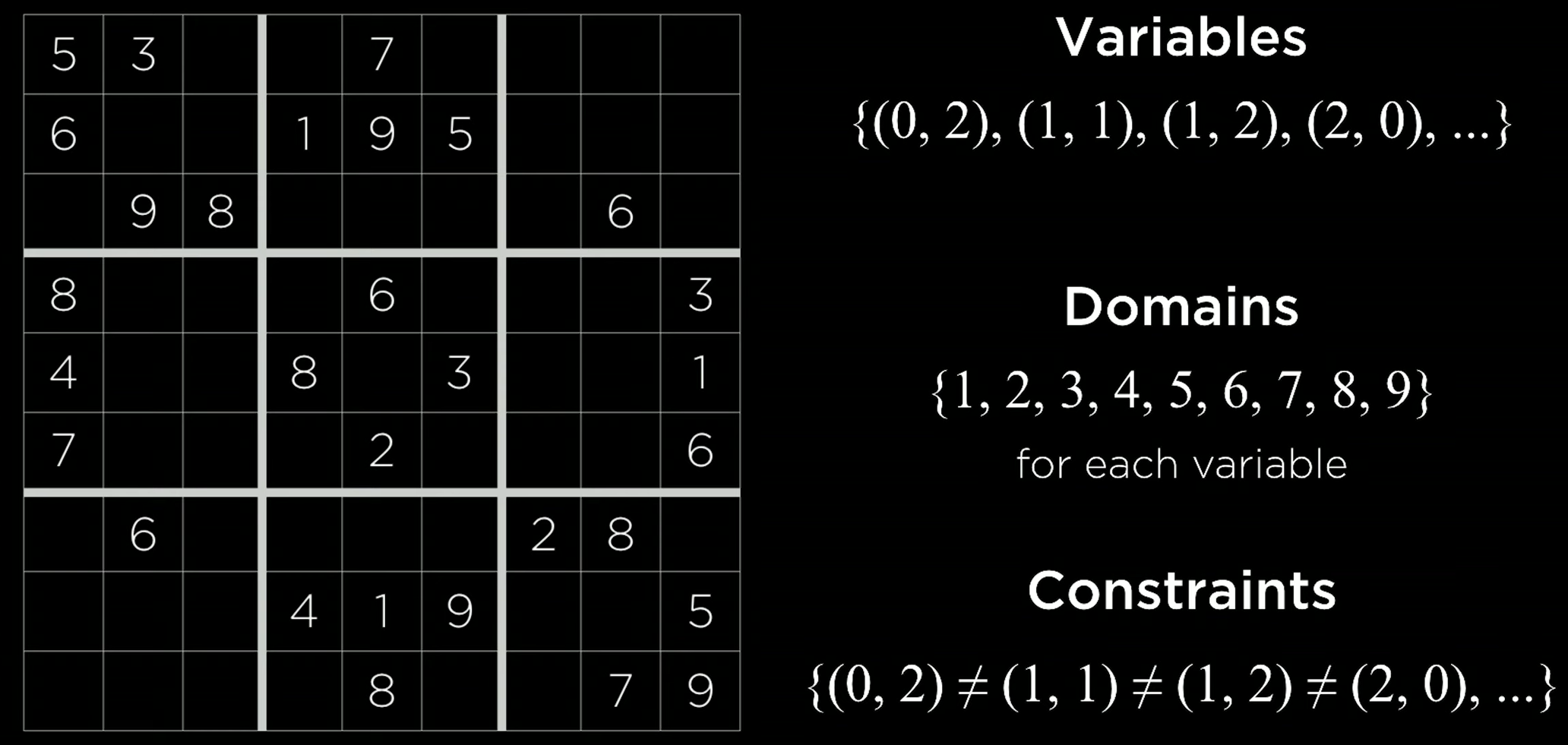
定义

• 变量集合：{X1, …, Xn}

• 每个变量的域（可取值）：{D1, …, Dn}

• 约束集合：对变量取值的限制（等于/不等/相邻不同等）

硬/软约束

• 硬约束：必须满足（如同一学生一天不能两门考试）

• 软约束：更像偏好，满足越多越优

一元/二元约束

• 一元：只涉及一个变量（如 A ≠ Mon）

• 二元：涉及两个变量（如 A ≠ B）

一致性：先削域再搜索，省大力气

• 节点一致性（Node Consistency）：域内每个值都满足一元约束 → 不合法的值直接删

• 弧一致性（Arc Consistency）：对弧 (X, Y)，保证 X 的每个值 在 Y 的域 中都有搭档可满足二元约束；没有就从 X 的域删掉

REVISE 与 AC-3 伪代码（删不合法的域值）：

REVISE(csp, X, Y):revised ← falsefor x in Domain(X):if ∄ y in Domain(Y) s.t. constraint(X, Y) satisfied:delete x from Domain(X)revised ← truereturn revisedAC-3(csp):Q ← all arcs (X, Y) in cspwhile Q not empty:(X, Y) ← pop(Q)if REVISE(csp, X, Y):if Domain(X) = ∅: return falsefor each Z in Neighbors(X) - {Y}:push (Z, X) into Qreturn true

小例：考试排程（课程 A–G，域是 Mon/Tue/Wed，约束是同学选的课不能同日），AC-3 能大幅缩小各课的可行日期，后面的搜索就容易多了。

---

5）把 CSP 当搜索：回溯 + 推理 = 实用解法

朴素回溯（Backtracking）

不断给未赋值变量尝试一个值；若违背约束则回退换值。

BACKTRACK(assignment, csp):if assignment complete: return assignmentX ← SELECT-UNASSIGNED-VAR(assignment, csp)for v in ORDERED-DOMAIN-VALUES(X, assignment, csp):if consistent(X=v, assignment, csp):add X=v to assignmentresult ← BACKTRACK(assignment, csp)if result ≠ failure: return resultremove X=v from assignmentreturn failure

让搜索“更聪明”的三板斧

1. 保持弧一致性（MAC）：每次新赋值后立刻跑一次 AC-3，把“不可能”的域值提前剪掉。

2. 选变量（变量排序）

   • MRV（最少剩余值）：先选域最小的变量，尽早发现死路；

   • 度启发式：若并列，选度最高（约束最多）的变量，能更快缩小其他域。

3. 选值（值排序）

   • 最少约束值（LCV）：优先尝试排除他人可能性最少的值，给后续“留活路”。

实战感受：MRV + 度启发式 + LCV + MAC 的组合，能让原本“回溯爆炸”的问题，秒变顺滑。考试排程、数独等都能明显受益。

Optimization - Lecture 3 - CS50…

---

6）用哪一个？一张对照表

你的问题长这样	建议首选	说明
只关心最终解，不在乎路径；邻域好定义	爬山 / 随机重启	快速、易实现；但可能卡局部最优
地形多坑、易卡局部最优	模拟退火	早期敢“变差”，后期稳；调好温度很关键
目标/约束全是线性的实数	线性规划（LP）	工业级算法（单纯形/内点），稳准狠
变量离散、约束繁多（排程/拼图/数独…）	CSP（回溯+MAC+启发式）	“先削域再搜索”，大幅提效

---

7）易错与复盘清单

• 邻域没定义清楚：局部搜索先把“邻居”定义严谨（TSP 常用 2-opt/3-opt）。

• 目标/代价混用：最大化就用“目标函数”，最小化就用“代价函数”，别混。

• 退火温度表太激进：降温太快=变成爬山；太慢=效率低。用指数或线性退火做 baseline。

• CSP 不先一致化：不做 AC-3 就硬回溯，常常平白多 10× 的搜索量。

• 忽略启发式：MRV/度/LCV 是“白拿”的效率红利。

注意：该文章为ai根据cs50ai视频与我的笔记生成，因逻辑清晰且更具阅读性而发布，仅供学习参考