LeetCode 994. 腐烂的橘子

 题目描述  

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

• 值 0 代表空单元格；
• 值 1 代表新鲜橘子；
• 值 2 代表腐烂的橘子。

每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。

返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

示例

示例 1：

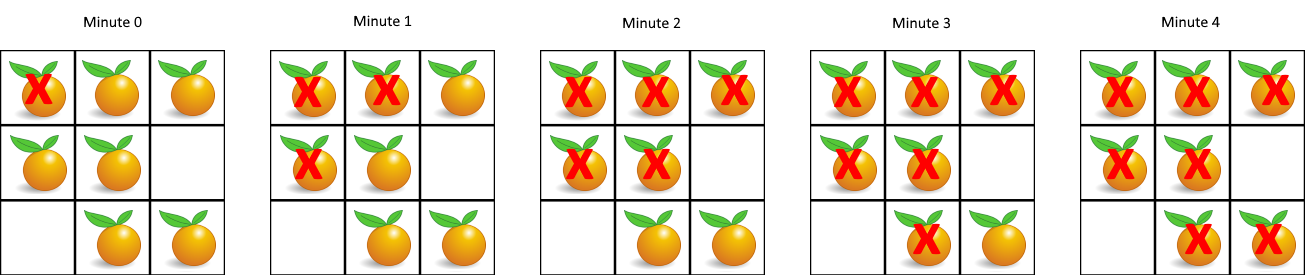
输入：grid = [[2,1,1],[1,1,0],[0,1,1]]
输出：4

示例 2：

输入：grid = [[2,1,1],[0,1,1],[1,0,1]]
输出：-1
解释：左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个方向上。

示例 3：

输入：grid = [[0,2]]
输出：0
解释：因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

解法

1.多源BFS腐蚀法

解题思路

       首先将腐烂的橘子装在一个栈中，fresh记录新鲜橘子的个数，后续会用到fresh,定义一个方位坐标容器，后续用于遍历，定义标志位rotten用来标记这一轮还有没有新鲜橘子变腐烂，如果有时间min++。每次处理所有的腐烂橘子（遍历栈），然后处理每个腐烂橘子四周的橘子，如果坐标满足条件且是新鲜的，则变腐烂，进栈，fresh--,rotten生效。最后返回用到fresh,它用于判断一开始就全为新鲜橘子这种情况返回-1。

class Solution {
public:int orangesRotting(vector<vector<int>>& grid) {int min = 0,fresh = 0;queue<pair<int,int>> q; //装腐烂的橘子vector<pair<int,int>> dex = {{-1,0},{0, -1},{1,0},{0,1}};for(int i = 0;i < grid.size();i ++){for(int j = 0;j < grid[0].size();j ++){if(grid[i][j] == 1) fresh ++;if(grid[i][j] == 2) q.push({i,j});}}bool rotten;while(!q.empty()){rotten = false;int n =  q.size();for(int i = 0;i < n;i ++){auto x = q.front();q.pop();for(auto d : dex){int i = x.first + d.first;int j = x.second + d.second;if(i >= 0 && i < grid.size() && j >= 0 && j < grid[0].size() && grid[i][j] == 1){grid[i][j] = 2;fresh --;q.push({i,j});rotten = true;}}}if(rotten) min ++;}return fresh == 0 ? min : -1;}
};

        时间复杂度O（MN），空间复杂度O（MN）