C++ 模拟题 力扣 6. Z字形变换 题解 每日一题

题目描述

题目链接：力扣 6. Z字形变换

题目描述：

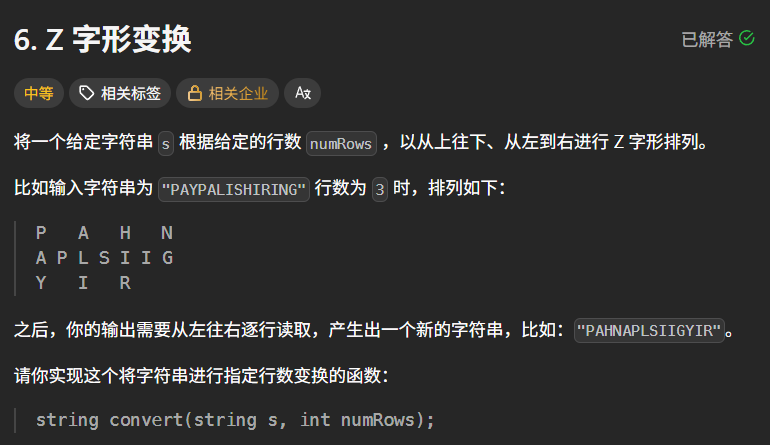
示例 1：
输入：s = “PAYPALISHIRING”, numRows = 3
输出：“PAHNAPLSIIGYIR”

示例 2：
输入：s = “PAYPALISHIRING”, numRows = 4
输出：“PINALSIGYAHRPI”
解释：如下图

0 1 2 3 4 5 6
P     I     N
A   L S   I G
Y A   H R
P     I

示例 3：
输入：s = “A”, numRows = 1
输出：“A”

提示：
1 <= s.length <= 1000
s 由英文字母（小写和大写）、‘,’ 和 ‘.’ 组成
1 <= numRows <= 1000

题目解析

咱们先把这道题的核心需求掰扯清楚——它不是真要咱们在屏幕上画个“Z”出来，而是让字符串按照“Z”的路径排列后，再按行读出来。说它是“N”字形其实更直观，毕竟字符是先从上到下铺满第一列，再斜着往右上走，到顶后又往下铺列，重复这个过程。

我们以示例2为例分析题目，如下图👇：

为什么这道题值得你花上几分钟弄懂？

首先，这道题是典型的“模拟转规律”题型——很多朋友拿到题会第一时间想“我能不能建个二维数组，按路径填字符再读出来”，但稍微想深一点就会发现“找规律”能大幅优化效率。这种“先暴力模拟，再优化规律”的思维，在数组、字符串类题目里太常用了，比如后面遇到的“螺旋矩阵”“杨辉三角”都能用类似思路解决。

其次，它的边界条件很典型：比如numRows=1的时候，根本不需要排列，直接返回原字符串；再比如字符串长度比行数还短，此时每行只有一个字符，也不用走“Z”路径。处理好这些边界，能帮你养成“先考虑特殊情况”的好习惯，避免提交时踩坑。

最后，它的时间复杂度优化很直观——从O(mn)（m是字符串长度，n是行数）降到O(m)，空间从O(mn)降到O(m)（只存结果），这种“降维打击”的优化过程，能帮你理解“为什么规律比模拟更高效”。

算法原理

模拟

先说说最容易想到的“笨办法”——模拟整个排列过程。具体怎么做呢？

第一步，建一个二维数组（或者vector<vector>），行数就是numRows，列数暂时不用定死（因为不知道要多少列）。第二步，确定字符的填写方向：一开始是“向下”，当填到第numRows-1行（最后一行）时，方向改成“斜右上”，当填到第0行（第一行）时，方向又改回“向下”。第三步，逐个遍历原字符串的字符，按方向填进二维数组里，直到所有字符填完。第四步，把二维数组按“行”拼接起来，就是最终结果。

举个例子，用示例1的“PAYPALISHIRING”和numRows=3：

• 先填P（0行0列）、A（1行0列）、Y（2行0列）——到最后一行了，方向改斜右上；
• next字符P，填到1行1列；再next字符A，方向改向下，填到0行2列；
• 就这么循环下去，最后数组按行读就是“PAHNAPLSIIGYIR”。

但这个方法的问题很明显：如果numRows很大（比如1000），字符串长度也1000，那二维数组大部分空间都是空的，纯属浪费；而且填数组的时候还要频繁改方向，代码写起来麻烦，效率也低。

优化

我们可以发现单纯模拟填写再遍历输出的时间复杂度是O(mn)，空间复杂度因为要开二维数组模拟也是O(mn)，综合来说这个方法并不理想，当数据范围变大很容易超时，所以我们要对其进行优化。

要点：所有的模拟优化最后都是归结于找规律

所以我们要找一找这道题的规律，我们画下图（因为字母不太好发现规律所以下面的图片我们都用字母在字符串中的下标代替字母）👇
我们还是以示例二为例：

这里的d = 2*numRows - 2是如何来的，我们看压缩之后的图（右下蓝色块）我们可以发现一个周期（一个蓝色块）里面的数字是2*numRows而因为是写成N字形会发现一个周期中（[0,1]和[3,1]）是没有字母的，所以要减去2，即d = 2*numRows - 2。
同理我们可以发现最后一排的规律与第一排相同，一个周期为 d = 2*numRows - 2

接下来我们找中间几排的规律，如下图👇：

其中我们以两个为一组的话，都在一个周期中我们知道一个位置就可以通过d来计算另一个的位置了。

有了这个规律，咱们就不用建数组了——直接按行遍历，根据规律算出每个字符的位置，拼到结果里就行，效率直接拉满！

代码实现

class Solution {
public:string convert(string s, int numRows) {// 计算Z字形排列中相邻两个完整列之间的步长int d = 2*(numRows - 1);int n = s.size();// 特殊情况处理：// 1. 只有一行时，无需变换直接返回// 2. 字符串长度小于行数时，也无需变换if(numRows == 1 || n < numRows)return s;// 存储结果的字符串string ret;// 处理第一行的字符// 第一行字符的索引规律：0, d, 2d, 3d...for(int i = 0; i < n; i += d)ret.push_back(s[i]);// 处理中间的行（从第2行到第numRows-1行）for(int k = 1; k < numRows - 1; k++){// 中间行每个周期有两个字符：// 一个在k, k+d, k+2d...位置// 另一个在d-k, d-k+d, d-k+2d...位置for(int i = k, j = d-k; i < n || j < n; i += d, j += d){// 添加第一个位置的字符（存在时）if(i < n) ret.push_back(s[i]);// 添加第二个位置的字符（存在时）if(j < n) ret.push_back(s[j]);}}// 处理最后一行的字符// 最后一行字符的索引规律：numRows-1, numRows-1+d, numRows-1+2d...for(int i = numRows - 1; i < n; i += d)ret.push_back(s[i]);return ret;}
};

时间复杂度和空间复杂度分析

• 时间复杂度：O(n)，其中n是字符串s的长度。咱们总共就遍历了一遍字符串里的每个字符——第一行、中间行、最后行加起来，每个字符只被访问一次，没有多余的循环，所以时间复杂度是线性的。

• 空间复杂度：O(n)（不考虑结果存储的话是O(1)）。这里的空间主要是用来存结果字符串ret，它的长度和原字符串s一样，都是n。除此之外，咱们只用到了几个变量（d、n、k、i、j），没有额外开数组或其他数据结构，所以额外空间是常数级的。

总结

这道题的核心思路就是“跳出模拟思维，找位置规律”——一开始可能会想建数组填字符，但只要多观察几行的下标分布，就能发现周期性规律，进而把时间和空间复杂度都降下来。

另外，边界条件的处理也很关键：比如numRows=1的时候，周期d会变成0，这时候循环会出问题，所以直接返回原字符串；再比如字符串长度比行数短，此时每个周期里只有“向下”的部分，没有“斜右上”的部分，直接按行取字符就行，这时候代码里的判断（i < n、j < n）也能帮咱们避免越界。

最后再回顾一下规律：周期d=2*(numRows-1)，第一行和最后一行是“起始位置+kd”，中间行是“k+d和kd -k”（k是周期次数）。记住这个规律，下次遇到类似的“路径排列”题，就能快速找到突破口啦！

下题预告

下一题咱们聚焦力扣 38. 外观数列。
它是“自我描述型”数列：第1项为"1"，后续每一项都是对前一项的字符计数描述（如第2项是“1个1”即"11"，第3项是“2个1”即"21"）。

题目要求给定整数n，返回第n项。解题关键在于实现“前项描述→后项生成”的迭代逻辑，同时注意n=1的边界处理。

下一次，咱们一起拆解这个迭代过程的代码实现，可以先试试自己推导前5项，提前感受字符计数与字符串拼接的核心逻辑~

如果这篇 Z 字形变换的解析帮你理清了思路，别忘了点赞支持一下呀！这样不仅能让更多需要的朋友看到，也能给我继续拆解算法题的动力～若想跟着节奏攻克下一道外观数列，记得关注我，后续更新会第一时间提醒你！觉得内容实用的话，还可以顺手收藏，万一以后复习算法时想回顾规律，打开就能看，省时又高效～