从递归到迭代吃透树的层次——力扣104.二叉树的最大深度

力扣104.二叉树的最大深度

---

一、题目分析

题目：
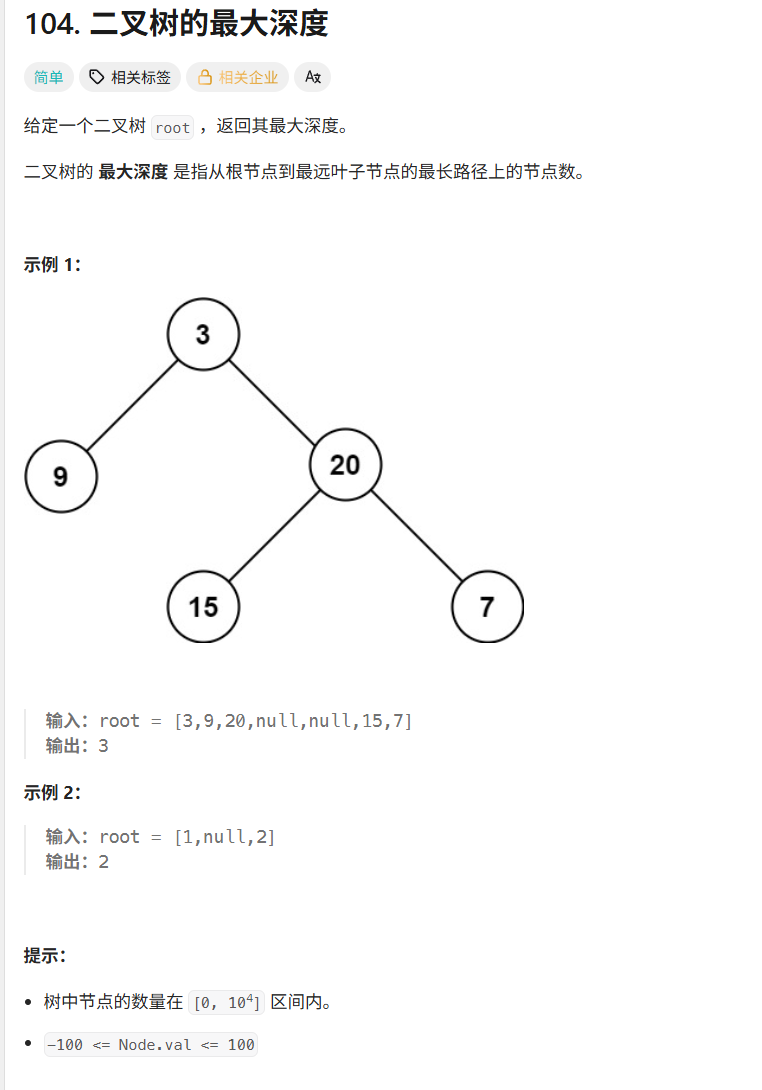
给定一棵二叉树的根节点 root，返回它的最大深度。
最大深度定义为：从根节点到最远叶子节点的最长路径上的节点数量。

输入输出示例：

输入	输出	说明
[3,9,20,null,null,15,7]	3	最长路径是 3 → 20 → 7
[1,null,2]	2	最长路径是 1 → 2

数据范围：

• 节点个数在 [0, 10^4]
• 节点值在 [-100, 100]

---

二、解法一：递归（深度优先）

思路：

• 若树为空，深度为 0。
• 否则，最大深度等于左右子树深度的最大值 + 1。
• 是最经典、最自然的思路。

public class Solution {public int maxDepth(TreeNode root) {if (root == null) return 0;int leftDepth = maxDepth(root.left);int rightDepth = maxDepth(root.right);return Math.max(leftDepth, rightDepth) + 1;}
}

复杂度分析：

• 时间复杂度：O(n)，每个节点遍历一次。
• 空间复杂度：O(h)，h 为树的高度（最坏情况下退化为 O(n)）。

---

三、解法二：层序遍历（BFS）

思路：

• 用队列逐层遍历，每遍历一层深度 +1。
• 最终层数即为最大深度。

import java.util.*;public class Solution {public int maxDepth(TreeNode root) {if (root == null) return 0;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);int depth = 0;while (!queue.isEmpty()) {int size = queue.size();for (int i = 0; i < size; i++) {TreeNode node = queue.poll();if (node.left != null) queue.offer(node.left);if (node.right != null) queue.offer(node.right);}depth++;}return depth;}
}

复杂度分析：

• 时间复杂度：O(n)，每个节点进出队各一次。
• 空间复杂度：O(n)，队列最多同时容纳一层节点。

---

四、解法三：显式栈（DFS 迭代版）

思路：

• 用栈模拟递归过程，栈中保存节点及其当前深度。
• 每次出栈时更新最大深度。

import java.util.*;public class Solution {public int maxDepth(TreeNode root) {if (root == null) return 0;Stack<TreeNode> nodeStack = new Stack<>();Stack<Integer> depthStack = new Stack<>();nodeStack.push(root);depthStack.push(1);int maxDepth = 0;while (!nodeStack.isEmpty()) {TreeNode node = nodeStack.pop();int depth = depthStack.pop();maxDepth = Math.max(maxDepth, depth);if (node.left != null) {nodeStack.push(node.left);depthStack.push(depth + 1);}if (node.right != null) {nodeStack.push(node.right);depthStack.push(depth + 1);}}return maxDepth;}
}

复杂度分析：

• 时间复杂度：O(n)
• 空间复杂度：O(n)

---

五、方法比较

方法	思路	是否递归	是否按层遍历	空间复杂度	优点
递归	自顶向下计算	✅	❌	O(h)	代码简洁直观
BFS	队列层序遍历	❌	✅	O(n)	层数一目了然
显式栈 DFS	手动栈模拟递归	❌	❌	O(n)	控制过程灵活