基于无监督深度学习方法的非迭代式、不确定性感知的磁共振成像肝脏脂肪定量评估|文献速递-文献分享

Title

题目

Non-iterative and uncertainty-aware MRI-based liver fat estimation using anunsupervised deep learning method

基于无监督深度学习方法的非迭代式、不确定性感知的磁共振成像肝脏脂肪定量评估

01

文献速递介绍

代谢相关性脂肪性肝病（MASLD）与肝脏脂肪定量评估研究背景及AI-DEAL方法概述 代谢相关性脂肪性肝病（Metabolic Associated Steatotic Liver Disease, MASLD）是一种全球性流行病，影响着近三分之一的世界人口（Loomba & Sanyal, 2013）。尽管MASLD具有可逆性，但它可能进一步发展为更复杂的疾病，如代谢功能障碍相关性脂肪性肝炎（Metabolic-dysfunction Associated Steatohepatitis, MASH）和肝硬化。MASLD是一类以肝细胞内脂质蓄积为特征的肝脏疾病谱系（Boldys & Buldak, 2024），因此，开发用于监测肝脏脂肪成分的技术已成为科学界关注的重点领域。 磁共振成像（Magnetic Resonance Imaging, MRI）是一种能够对甘油三酯分子进行定量分析的医学成像技术。通过化学位移编码（chemical shift-encoded, CSE）MRI协议，可将采集到的磁共振信号分离为纯水质子信号与纯脂肪质子信号。在此基础上，能够估算出定量生物标志物——质子密度脂肪分数（Proton Density Fat Fraction, PDFF），其定义为纯脂肪质子密度与总质子密度的比值。以往研究已证实，PDFF与MASLD之间存在强相关性（Idilman et al., 2013; Yokoo et al., 2018）。 通常情况下，PDFF的估算采用非线性最小二乘法，计算纯水质子信号与纯脂肪质子信号，同时需考虑干扰因素（如(R_2^*)信号衰减、主磁场不均匀性）。在这类方法中，Hernando等人（2010）提出的基于迭代图割（Graph Cut）的技术常被视为基准方法，因其PDFF估算无偏且对磁场不均匀性具有稳健性。然而，该图割方法通常需要至少6个回波信号作为输入，以获得最优信噪比（signal-to-noise ratio, SNR）的结果，根据所选的磁共振扫描参数（如分辨率、视野等），这可能导致较长的扫描时间。此外，图割方法因其迭代特性，计算成本较高，且可能需要对部分参数进行精细调整。 近年来提出的基于深度学习（Deep Learning, DL）的PDFF估算方法，与非深度学习方法相比，展现出了良好的准确性，并缩短了后处理时间（Andersson et al., 2019; Goldfarb et al., 2019; Cho & Park, 2019; Liu et al., 2020; Jafari et al., 2021; Shih et al., 2021, 2022; Meneses et al., 2023）。此外，部分此类方法还通过减少所需的MRI数据量，实现了采集时间的缩短（Goldfarb et al., 2019; Meneses et al., 2023）。但值得注意的是，上述多数方法需要带有基准结果的标注训练数据，而这些基准结果需通过非最优的现有脂肪定量技术获取。 当前基于深度学习的PDFF估算方法向临床实践转化的另一重要局限在于其泛化能力较差。大量文献表明，用于MRI相关任务的深度学习方法在训练数据集与测试数据集存在域偏移（如图像对比度、解剖区域、采集策略的变化）时，会面临巨大挑战（Wang et al., 2025; Yoon et al., 2024; Cheng et al., 2025; Sarafraz et al., 2024）。与之相反，基于图割优化等传统PDFF定量方法（Hernando et al., 2010）虽非完美，但已被证实在不同磁共振扫描仪厂商及扫描协议下具有良好的可重复性（Hernando et al., 2010; Daudé et al., 2023; Yokoo et al., 2018）。考虑到深度学习方法的“黑箱”特性使其推理过程难以解释（Kabir et al., 2022），其泛化能力差的问题显得更为关键。因此，在缺乏可用基准结果的情况下，很难判断基于深度学习的模型性能不佳是否源于测试数据与训练数据分布的域偏移。 为解决这些局限，Shih等人（2022）提出采用具有不确定性感知的深度学习方法，该方法不仅能估算任务特定输出，还能输出与估算的水脂分离信号置信度相关的不确定性值（即方差）。但该方法专为联合重建与水脂分离任务设计，且其模型训练依赖基准结果的获取，而基准结果的计算需耗费大量工时与计算资源。 此前，Tamada等人（2024）也对MRI水脂分离中的置信度估算进行了研究，提出一种基于拟合优度的非深度学习方法来估算置信度图谱。然而，该方法未考虑对最终PDFF结果进行显式方差计算，且针对不同误差来源（如低信噪比、水脂信号交换、高磁化率物体引发的伪影），需设计不同的手工置信度图谱。此外，作者指出该方法计算成本较高（约5分钟/病例），且需进一步验证以评估其算法的可重复性（Tamada et al., 2024）。 本研究提出一种基于人工智能的水脂分解方法——AI-DEAL（基于回波不对称性与最小二乘法的人工智能水脂分解法，Artificial Intelligence-based Decomposition of water and fat with Echo Asymmetry and Least-squares），用于从CSE-MRI数据中估算肝脏PDFF。该方法采用基于物理原理的无监督损失函数进行训练，因此无需任何基准结果。AI-DEAL为估算不确定性图谱提供了理论框架，该不确定性图谱与通过快速非迭代过程获得的纯水质子信号、纯脂肪质子信号相关。AI-DEAL的主要目标是在较短计算时间内，提供辅助性的PDFF不确定性图谱，以指示PDFF估算结果的置信度。研究假设，当在与训练数据库存在域偏移的样本（如易产生伪影的区域、解剖结构变化、扫描协议变化）上进行测试时，观察到的PDFF偏差会与较高的PDFF方差相关。 本文结构如下：第2节介绍与基于MRI的脂肪定量技术相关的理论框架；第3节阐述所用数据、AI-DEAL框架及本研究中涉及的其他基于深度学习的对比模型；第4节描述利用所有可用数据开展的实验，以评估PDFF不确定性估算对域偏移可能引发的PDFF偏差的敏感性；第5节呈现实验结果；最后，第6节与第7节对观察到的结果进行讨论并得出结论。

Aastract

摘要

Liver proton density fat fraction (PDFF), the ratio between fat-only and overall proton densities, is anextensively validated biomarker associated with several diseases. In recent years, numerous deep learningbased methods for estimating PDFF have been proposed to optimize acquisition and post-processing timeswithout sacrificing accuracy, compared to conventional methods. However, the lack of interpretability and theoften poor generalizability of these DL-based models undermine the adoption of such techniques in clinicalpractice.In this work, we propose an Artificial Intelligence-based Decomposition of water and fat with EchoAsymmetry and Least-squares (AI-DEAL) method, designed to estimate both proton density fat fraction (PDFF)and the associated uncertainty maps. Once trained, AI-DEAL performs a one-shot MRI water-fat separation byfirst calculating the nonlinear confounder variables, 𝑅∗ 2 and off-resonance field. It then employs a weightedleast squares approach to compute water-only and fat-only signals, along with their corresponding covariancematrix, which are subsequently used to derive the PDFF and its associated uncertainty.We validated our method using in vivo liver CSE-MRI, a fat-water phantom, and a numerical phantom.AI-DEAL demonstrated PDFF biases of 0.25% and −0.12% at two liver ROIs, outperforming state-of-the-artdeep learning-based techniques. Although trained using in vivo data, our method exhibited PDFF biases of−3.43% in the fat-water phantom and −0.22% in the numerical phantom with no added noise. The latter biasremained approximately constant when noise was introduced. Furthermore, the estimated uncertainties showedgood agreement with the observed errors and the variations within each ROI, highlighting their potential value

肝脏质子密度脂肪分数（PDFF）相关研究摘要 肝脏质子密度脂肪分数（PDFF，即纯脂肪质子密度与总质子密度的比值）是一种经过广泛验证的生物标志物，与多种疾病相关。近年来，学界已提出众多基于深度学习的PDFF估算方法。与传统方法相比，这些方法在不损失准确性的前提下，优化了数据采集与后处理时间。然而，此类深度学习模型普遍存在可解释性不足、泛化能力较差的问题，这在一定程度上阻碍了其在临床实践中的应用。 本研究提出一种基于人工智能的水脂分解方法——AI-DEAL（基于回波不对称性与最小二乘法的人工智能水脂分解法），该方法可同时估算质子密度脂肪分数（PDFF）及相关不确定性图谱。AI-DEAL训练完成后，能通过“一步式”磁共振水脂分离实现PDFF估算：首先计算非线性干扰变量（(R_2^*) 与偏共振场），随后采用加权最小二乘法计算纯水质子信号与纯脂肪质子信号，以及二者对应的协方差矩阵，最终基于这些数据推导得到PDFF及其相关不确定性图谱。 研究团队通过在体肝脏CSE-MRI（化学位移编码磁共振成像）数据、水脂体模数据及数值体模数据上对该方法进行验证。结果显示：在肝脏两个感兴趣区域（ROI）中，AI-DEAL的PDFF偏差分别为0.25%和-0.12%，性能优于当前主流的基于深度学习的技术；尽管该方法仅使用在体数据训练，但在水脂体模中PDFF偏差为-3.43%，在无附加噪声的数值体模中PDFF偏差为-0.22%，且引入噪声后，数值体模中的偏差基本保持稳定。此外，估算得到的不确定性图谱与观测误差及各感兴趣区域内的变异度具有良好的一致性，这凸显了该方法在临床应用中的潜在价值。

Method

方法

3.1. Available data

To develop and validate our proposed method, we considered asingle-site liver CSE-MRI database composed of 2D multi-slice acquisitions from 206 subjects (117 females, mean age 36.5 y/o) withsuspected hepatic steatosis. This single site was equipped with a 1.5Tscanner (Achieva, Philips Healthcare, Best, The Netherlands). Thisstudy was IRB-approved, and all participants signed an informed consent form. The entire dataset consisted of 4577 axial slices. For eachscan, magnitude and phase data were acquired at six echo times (TEs),first at TE1 = 1.3 ms and 𝛥TE = 2.1 ms. The number of acquired slicesvaried according to each case, since it was set to cover the entire liver.The MR acquisition parameters are shown in Table 1.The liver CSE-MRI database was split into training (150 subjects),validation (18), and testing (38) subsets. According to reference liverPDFF values obtained with Graph Cuts, the training database included26 subjects with no steatosis (PDFF < 5.2%), 42 with mild steatosis(5.2 ≤ PDFF < 11.3%), 21 with moderate steatosis (11.1 ≤ PDFF <17.1%), and 61 with severe steatosis (PDFF ≥ 17.1%) (Tang et al., 2015).For validation purposes only, we also considered a single CSE-MRIscan available in the Multisite and multivendor fat-water phantomdataset (Hernando et al., 2017) and a numerical phantom with sevenvials of different fat fraction values, 𝑅∗ 2 , and magnetic susceptibilities(Fig. 1). The phantom was generated using the physical model in Eq. (1)and customized echo times.The primary purpose of this numerical phantom was to isolate thesignal from any other sources of error that might occur in vivo and toobserve the relationship between the PDFF variance and the observedPDFF errors. Moreover, similar to the fat-water phantom, the numericalphantom was also useful for observing the robustness of our neuralnetworks to out-of-distribution data (i.e., samples that significantlydiffer from the training dataset). We also used this simulated phantomto perform a sensitivity analysis of the PDFF error caused by the R2*and 𝜙 biases.MATLAB (R2023 b) was used to develop the preprocessing of theliver CSE-MRI data and the fat-water phantom simulations.

3.1 可用数据 为开发并验证所提出的方法，本研究采用了单中心肝脏化学位移编码磁共振成像（CSE-MRI）数据库。该数据库包含206名疑似肝脂肪变性受试者（117名女性，平均年龄36.5岁）的二维多层采集数据，数据采集于一台1.5T磁共振扫描仪（Achieva，飞利浦医疗系统，荷兰贝斯特）。本研究已获得机构审查委员会（IRB）批准，所有受试者均签署了知情同意书。 整个数据库包含4577层轴位图像。每次扫描均在6个回波时间（TE）下采集幅度与相位数据，首个回波时间（TE1）为1.3ms，回波时间间隔（ΔTE）为2.1ms。采集的图像层数因受试者情况而异，以确保覆盖整个肝脏。磁共振采集参数详见表1。 该肝脏CSE-MRI数据库被划分为训练集（150名受试者）、验证集（18名受试者）与测试集（38名受试者）。根据通过图割法（Graph Cuts）获得的参考肝脏质子密度脂肪分数（PDFF）值，训练集包含26名无脂肪变性受试者（PDFF<5.2%）、42名轻度脂肪变性受试者（5.2≤PDFF<11.3%）、21名中度脂肪变性受试者（11.1≤PDFF<17.1%）及61名重度脂肪变性受试者（PDFF≥17.1%）（Tang et al., 2015）。 仅为验证目的，本研究还采用了以下两类数据：一是多中心多厂商水脂体模数据库（Hernando et al., 2017）中的一次CSE-MRI扫描数据；二是包含7个不同脂肪分数、(R_2^)值及磁化率值样本管的数值体模（图1）。该数值体模通过公式（1）中的物理模型及定制化回波时间生成。 该数值体模的主要用途包括：分离在体数据中可能存在的其他误差源信号，观察PDFF方差与观测PDFF误差之间的关系；与水脂体模类似，用于评估神经网络对分布外数据（即与训练数据集差异显著的样本）的稳健性。此外，本研究还利用该模拟体模，对由(R_2^)偏差和偏共振场（(\phi)）偏差引起的PDFF误差进行敏感性分析。 肝脏CSE-MRI数据的预处理及水脂体模模拟均采用MATLAB（R2023b）软件实现。

Conclusion

结论

AI-DEAL represents a novel method for quantifying liver PDFF,along with 𝑅∗ 2 and off-resonance field maps, using both deep learningand the underlying physics of the MR signal generation process. Ourmethod also enables the generation of uncertainty maps, which areproven to be closely related to the error of the measurements andthe presence of artifacts such as noise and phase errors. The provideduncertainty maps and the physics-informed nature of AI-DEAL givean improved interpretability to our method compared to previouslyproposed DL-based algorithms. We hypothesize that uncertainty estimations, which quantitatively describe the reliability of the resultingparametric maps at each location, have potential value for clinicians toassess the reliability of MRI-based fat composition estimates at differentliver regions. The usefulness of the uncertainty maps for downstreamtasks will be further validated in future work.

AI-DEAL：一种新型肝脏PDFF定量方法 AI-DEAL是一种新型肝脏质子密度脂肪分数（PDFF）定量方法，同时可用于定量(R_2^*)与偏共振场图谱。该方法结合了深度学习技术与磁共振（MR）信号产生过程的基础物理原理。 本方法还能够生成不确定性图谱，经证实，这类图谱与测量误差、噪声及相位误差等伪影的存在密切相关。与此前提出的基于深度学习（DL）的算法相比，AI-DEAL提供的不确定性图谱及其物理知情特性，提升了该方法的可解释性。 我们推测，不确定性估算具有潜在应用价值，可为临床医生评估不同肝脏区域基于MRI的脂肪成分估算可靠性提供参考。其中，不确定性估算能够定量描述各位置所得参数图谱的可靠性。未来研究将进一步验证不确定性图谱在下游任务中的实用性。 要不要我帮你提炼这份内容的核心技术亮点与临床价值总结？

Results

结果

5.1. Evaluation on liver CSE-MRI

Fig. 4 shows an example set of all the output quantitative maps,along with their respective variance maps, obtained using AI-DEAL anda CSE-MRI scan from a testing subject.

5.1.1. PDFF bias analysis

Considering PDFF estimates in the RHL, the bias (±𝑆𝐷) of AI-DEALwas 0.25± 0.68%. In contrast, the biases of VET-Net, MDWF-Net, and UNet in this same ROI were −0.58±0.68%, −0.44±1.95%, and 0.54±2.13%,respectively.On the other hand, PDFF biases in the LHL were −0.12 ± 0.42% forAI-DEAL, −0.32 ± 0.60% for VET-Net, −0.04 ± 2.06% for MDWF-Net, and0.46 ± 2.00% for U-Net. Both RHL and LHL PDFF biases observed foreach method are summarized in Table 2. Additionally, the PDFF mapsobtained for a specific testing sample using all the available DL-basedmethods are shown in Fig. 5.

5.1.2. Uncertainty analysis

The multiple linear regression analysis demonstrated a mild correlation (𝑅2 = 0.20, 𝑝 = 0.0163) between the two independent variables(PDFF absolute error & PDFF IQ range) and the PDFF variance. The 3Dmulti-regression plot is shown in Fig. 6.

5.1 肝脏化学位移编码磁共振成像（CSE-MRI）评估结果 图4展示了利用AI-DEAL方法对一名测试受试者的CSE-MRI扫描数据进行处理后，得到的所有输出定量图谱示例及其各自的方差图谱。 ## 5.1.1 质子密度脂肪分数（PDFF）偏差分析 在肝右叶（RHL）的PDFF估算中，AI-DEAL的偏差（±标准差，±SD）为0.25±0.68%。相比之下，在同一感兴趣区域（ROI）中，VET-Net、MDWF-Net和U-Net的偏差分别为-0.58±0.68%、-0.44±1.95%和0.54±2.13%。 在肝左叶（LHL）的PDFF估算中，AI-DEAL的偏差为-0.12±0.42%，VET-Net的偏差为-0.32±0.60%，MDWF-Net的偏差为-0.04±2.06%，U-Net的偏差为0.46±2.00%。表2汇总了各方法在肝右叶和肝左叶的PDFF偏差结果。此外，图5展示了采用所有可用的基于深度学习（DL）的方法，对某一特定测试样本进行处理后得到的PDFF图谱。 ## 5.1.2 不确定性分析 多元线性回归分析结果显示，两个自变量（PDFF绝对误差与PDFF四分位距，PDFF IQ range）与PDFF方差之间存在弱相关性（决定系数(R^2=0.20)，概率值(p=0.0163)）。该三维多元回归图如图6所示。

Figure

图

Fig. 1. Simulated phantom. First row: Quantitative parameters required to simulate CSE-MRI (using Eq. (1)). The off-resonance field map 𝜙 is calculated as thesum of the linear field inhomogeneity and the susceptibility field map. Second row: Magnitude and phase CSE-MRI data at the first three echoes.

图1 模拟体模 第一行：模拟化学位移编码磁共振成像（CSE-MRI）所需的定量参数（使用公式（1））。偏共振场图(\boldsymbol{\phi})通过线性磁场不均匀性与磁化率场图之和计算得出。 第二行：前三个回波的化学位移编码磁共振成像（CSE-MRI）幅度数据与相位数据。

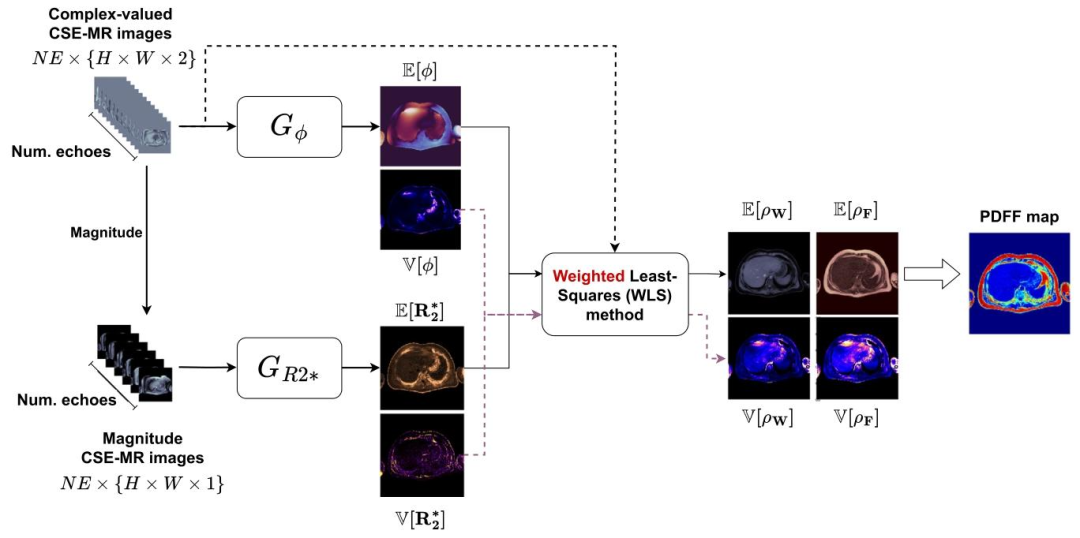
Fig. 2. AI-DEAL framework. Two convolutional neural networks with probabilistic output layers calculate the mean and variance of 𝑅∗ 2 and 𝜙 maps. Then, themean and covariance matrix of 𝜌 are estimated using the weighted least squares (WLS) method.

图2 AI-DEAL框架 包含概率输出层的两个卷积神经网络用于计算(R_2^*)图与偏共振场（(\phi)）图的均值和方差。随后，采用加权最小二乘法（WLS）估算质子密度（(\rho)）的均值与协方差矩阵。

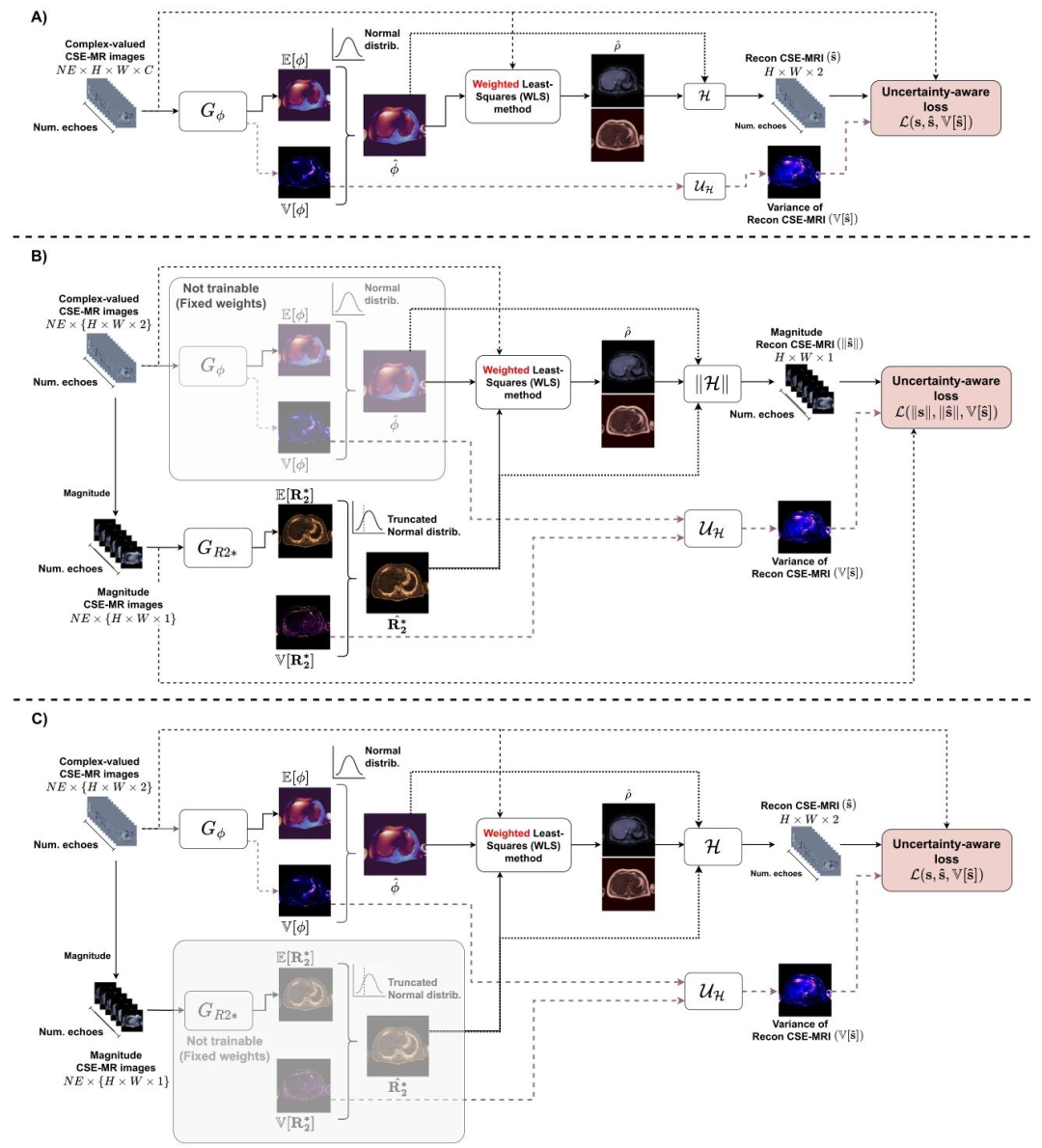
Fig. 3. Summary of AI-DEAL training stages. (A) First stage for a coarse fitting of 𝐺𝜙 . (B) Magnitude-based fitting of 𝐺𝑅2. (C) Final fine-tuning stage, similar toA but considering the 𝑅∗ 2 map estimated by 𝐺𝑅2∗ to obtain the reconstructed CSE-MRI and its variance

图3 AI-DEAL训练阶段总结 （A）第一阶段：对偏共振场预测网络（(G{\phi})）进行粗略拟合。   （B）基于幅度的拟合阶段：对(R_2^)预测网络（(G{R2^})）进行拟合。   （C）最终微调阶段：流程与（A）类似，但需结合(G_{R2^})估算得到的(R_2^*)图，以获取重建的化学位移编码磁共振成像（CSE-MRI）数据及其方差。

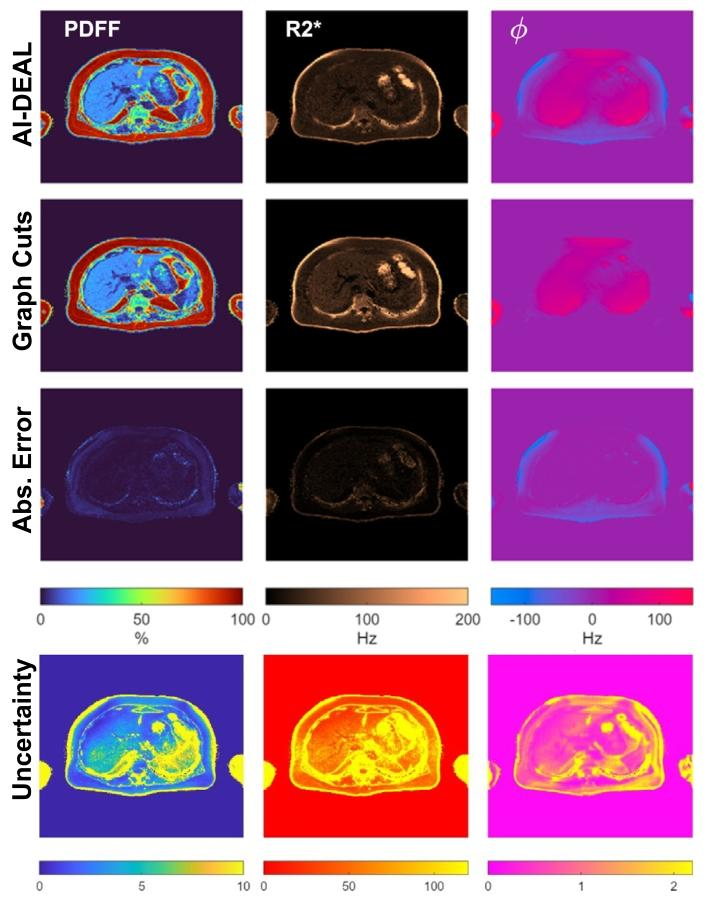
Fig. 4. Visualization of the quantitative maps estimated by AI-DEAL, alongwith their uncertainty maps, obtained from a testing CSE-MRI sample. Differences with respect to the reference Graph Cuts estimations are also depicted.

图4 AI-DEAL估算的定量图谱及其不确定性图谱可视化 图中展示了从某测试化学位移编码磁共振成像（CSE-MRI）样本中，通过AI-DEAL方法获得的定量图谱及其对应的不确定性图谱；同时还呈现了这些图谱与图割法（Graph Cuts）基准估算结果的差异。

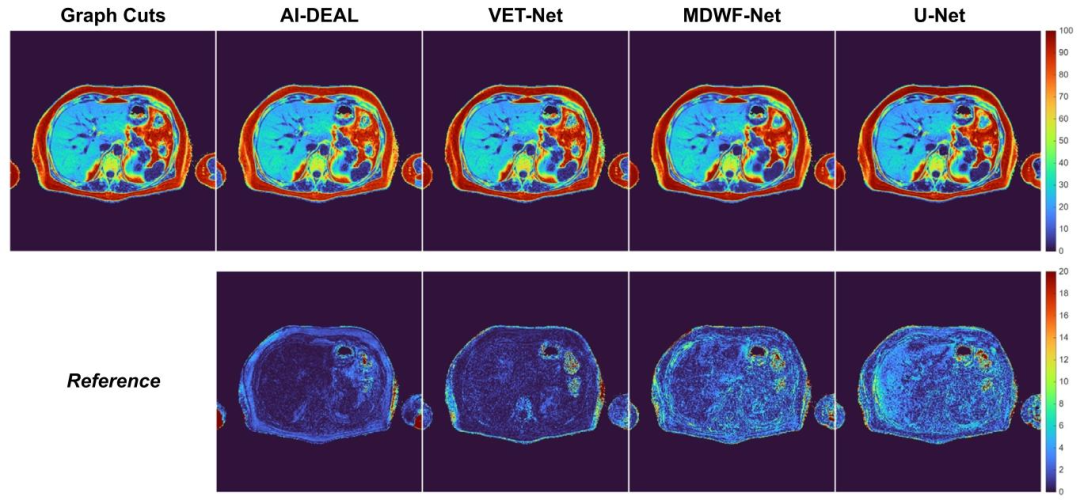
Fig. 5. PDFF maps obtained using all DL-based methods for a testing sample. PDFF absolute error maps are depicted in the bottom row.

图5 采用所有基于深度学习（DL）的方法对某测试样本获得的质子密度脂肪分数（PDFF）图谱 下方一行展示的是PDFF绝对误差图谱

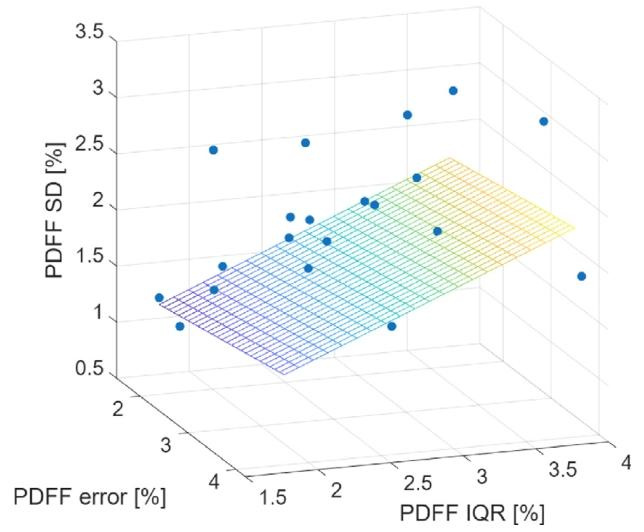
Fig. 6. Multiple linear regression analysis for PDFF estimations at the RHL.

图6 肝右叶（RHL）质子密度脂肪分数（PDFF）估算结果的多元线性回归分析

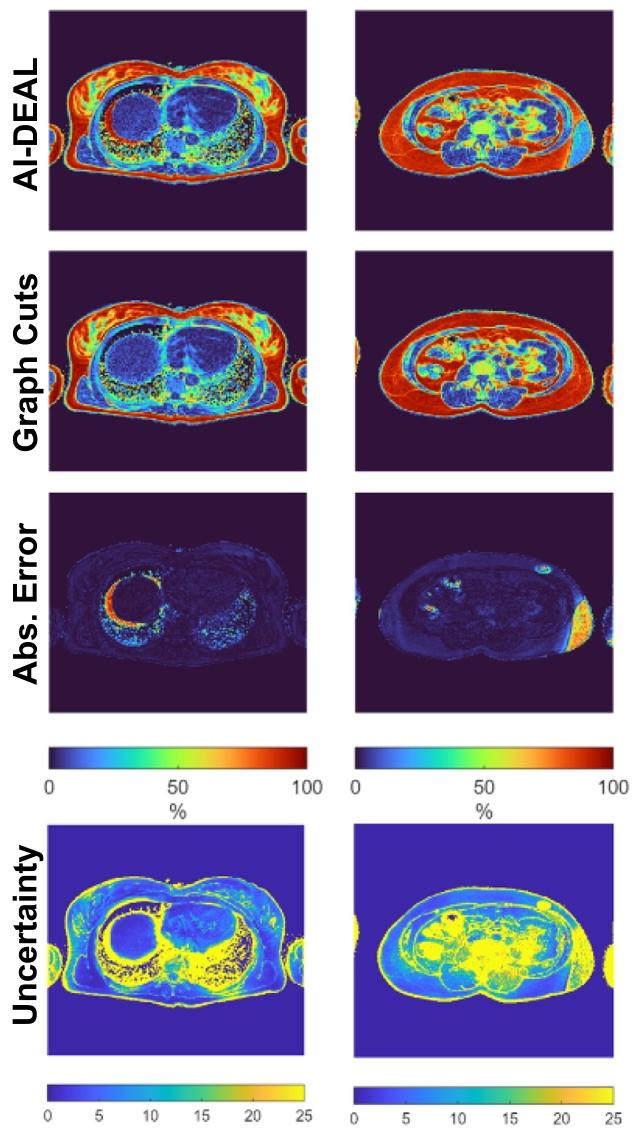
Fig. 7. PDFF maps and their respective uncertainties for two critical scenarios:Liver dome (left column) and lower abdomen (right column)

图7 两种关键场景下的质子密度脂肪分数（PDFF）图谱及其各自的不确定性图谱 左栏为肝顶部场景，右栏为下腹部场景。

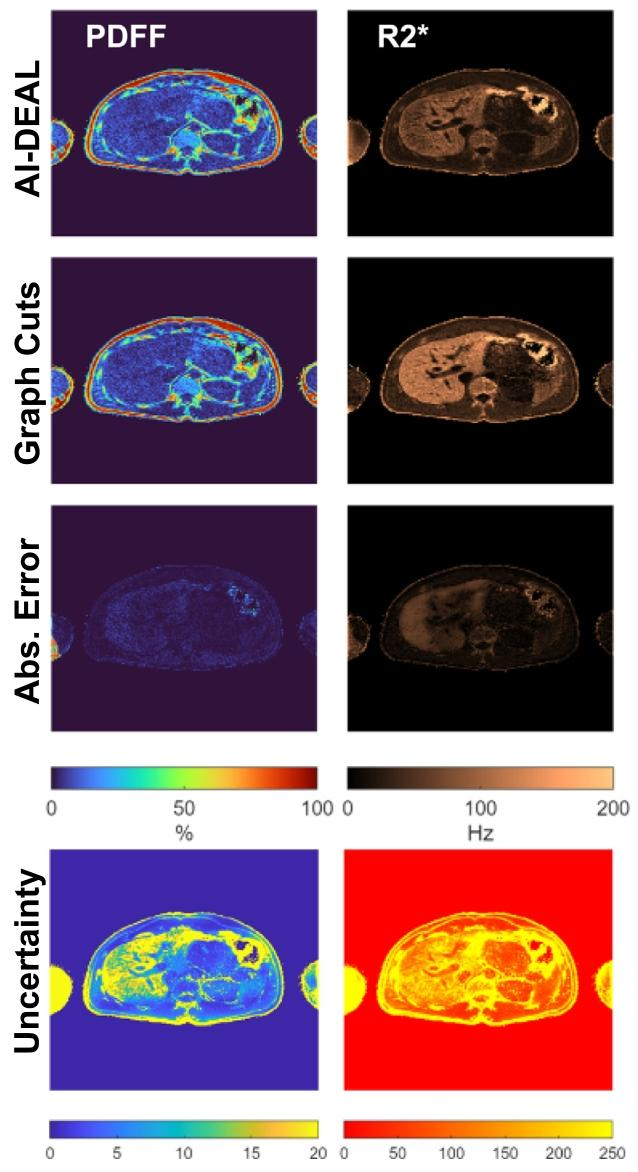
Fig. 8. PDFF and 𝑅∗ 2 predictions obtained with AI-DEAL, along with therelated uncertainty maps

图8 AI-DEAL方法获得的质子密度脂肪分数（PDFF）与(R_2^)预测结果，及相关不确定性图谱

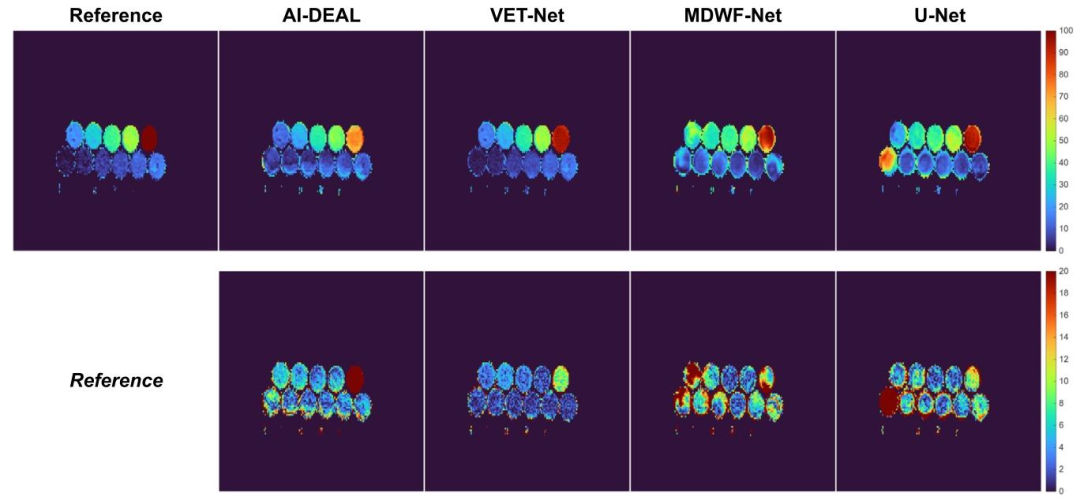
Fig. 9. PDFF maps obtained using all implemented DL-based methods on the multi-site fat-water phantom.

图9 采用所有已实现的基于深度学习（DL）的方法，在多中心水脂体模上获得的质子密度脂肪分数（PDFF）图谱

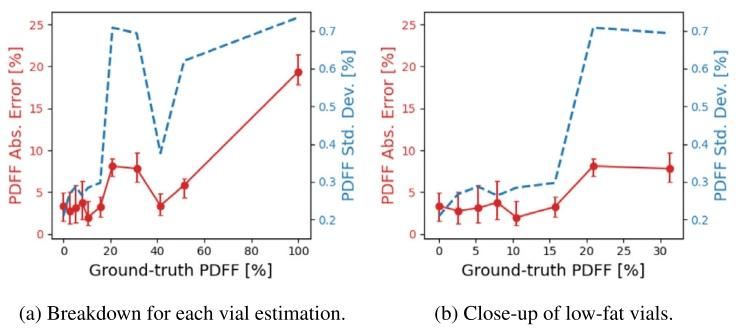
Fig. 10. PDFF absolute errors v/s uncertainties at the vials of the fat-waterphantom. The red dots correspond the median of the PDFF absolute errorwithin each vial, and the error bars depict the IQ range. Blue dashed linescorrespond to the PDFF uncertainty values.

图10 水脂体模各样本管处的质子密度脂肪分数（PDFF）绝对误差与不确定性对比 红色圆点代表每个样本管内PDFF绝对误差的中位数，误差线表示四分位距（IQ range）。蓝色虚线代表PDFF不确定性数值。

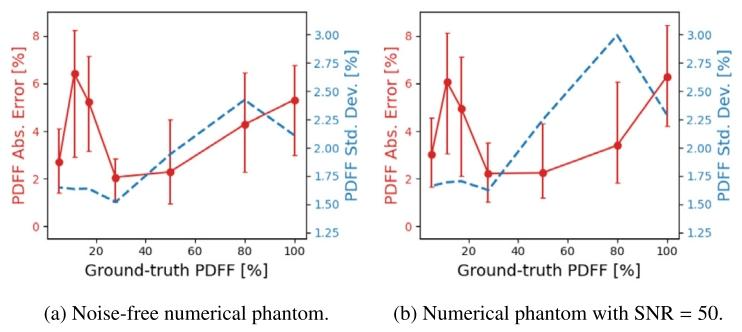
Fig. 11. PDFF absolute errors v/s uncertainties at the vials of the numericalphantom. The red dots correspond to the median of the PDFF absolute errorwithin each vial, and the error bars depict the IQ range. Blue dashed linescorrespond to the PDFF uncertainty values.

图11 数值体模各样本管处的质子密度脂肪分数（PDFF）绝对误差与不确定性对比 红色圆点代表每个样本管内PDFF绝对误差的中位数，误差线表示四分位距（IQ range）。蓝色虚线代表PDFF不确定性数值。

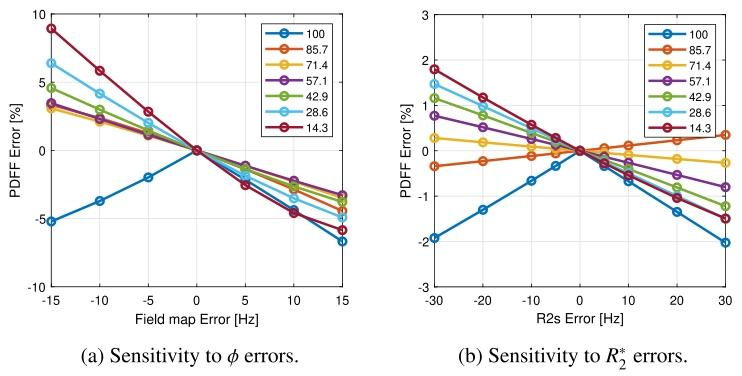
Fig. 12. PDFF sensitivity to different 𝜙 and 𝑅 2 error levels.

图12 质子密度脂肪分数（PDFF）对不同偏共振场（(\phi)）和(R_2^*)误差水平的敏感性

Table

表

Table 1MR scan acquisition parameters of the used pulse sequence

表1 所用脉冲序列的磁共振扫描采集参数

Table 2PDFF biases obtained in the liver CSE-MRI testing subset for each of the implemented Deep Learning. Estimations obtained with6-echo Graph Cuts were considered as reference. ∗ Phantom CSE-MRI data has echo times different from the training protocol(Table 1), and VET-Net is the only DL-based model designed to handle such variation

表2 各已实现深度学习方法在肝脏化学位移编码磁共振成像（CSE-MRI）测试子集上获得的质子密度脂肪分数（PDFF）偏差 以6回波图割法（Graph Cuts）获得的估算结果作为基准。 * 注：体模CSE-MRI数据的回波时间与训练协议（表1）不同，而VET-Net是唯一一种设计用于处理此类差异的基于深度学习（DL）的模型。

Table 3Breakdown of the PDFF biases observed at each vial of the simulated phantom for each of the implemented deep learning methods.The PDFF standard deviations estimated by AI-DEAL are also included

表3 各已实现深度学习方法在模拟体模各样本管上观察到的质子密度脂肪分数（PDFF）偏差明细 表中还包含了AI-DEAL估算得到的PDFF标准差。

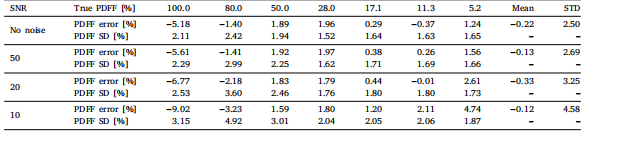
Table 4The performance of our LF-MRI on the fastMRI PD dataset in terms of using different classification networks to perform weaklysupervised localization for lesion-enhanced imaging

表4 病灶导向磁共振成像（LF-MRI）在fastMRI PD（质子密度加权）数据集上的性能表现 该表评估了使用不同分类网络执行弱监督定位以实现病灶增强成像时，LF-MRI的性能差异。