图像处理(三)--开运算与闭运算,梯度运算,礼帽与黑帽
目录
1、开运算与闭运算
1.1 腐蚀与膨胀
1.2 开运算(Opening):先腐蚀,后膨胀
1.2.1 定义
1.2.2 核心作用
1.2.3 示例(二值图像)
1.3 闭运算(Closing):先膨胀,后腐蚀
1.3.1 定义
1.3.2 核心作用
1.3.3 示例(二值图像)
1.4 开运算 vs 闭运算:关键差异对比
1.5 代码实现(OpenCV-Python)
1.6 扩展:灰度图像的开 / 闭运算
2、梯度运算
2.1 梯度运算的数学基础
2.2 常用梯度算子
2.3 梯度运算的作用
2.4 OpenCV 代码实现(Python)
2.5 注意事项
3、礼帽与黑帽
3.1 礼帽运算:
3.2 黑帽运算:
1、开运算与闭运算
开运算(Opening)和闭运算(Closing)是数学形态学(Mathematical Morphology) 的核心操作,基于「腐蚀(Erosion)」和「膨胀(Dilation)」组合实现,主要用于处理二值图像(黑白图像)的噪声去除、轮廓修正、孔洞填充等任务,也可扩展到灰度图像。
1.1 腐蚀与膨胀
在理解开 / 闭运算前,需先明确两个基础操作的作用(以二值图像为例,白色为前景目标,黑色为背景):
操作 核心效果 直观理解
腐蚀 前景目标边界被 “侵蚀”,小的前景区域(如噪声点)会被消除,目标尺寸缩小。 用 “结构元素”“啃食” 前景边缘
膨胀 前景目标边界向外 “扩张”,小的背景孔洞会被填充,目标尺寸增大。 用 “结构元素”“扩充” 前景边缘
其中,结构元素(Structuring Element) 是形态学操作的 “工具”(通常为 3×3、5×5 的正方形 / 圆形矩阵),决定了操作的范围和方向。
1.2 开运算(Opening):先腐蚀,后膨胀
1.2.1 定义
开运算 = 腐蚀(Erosion)→ 膨胀(Dilation)先通过腐蚀消除小的前景噪声,再通过膨胀恢复目标的原始尺寸(但已消除的噪声不会恢复)。
1.2.2 核心作用
去除小的前景噪声:比如图像中孤立的白色小点(噪声),会被腐蚀完全消除,后续膨胀仅恢复大目标的尺寸。
分离粘连的目标:若两个前景目标有轻微粘连,腐蚀会切断粘连处,后续膨胀可让目标独立且恢复原有形状。
保留大目标的形状和位置:对大的前景目标,腐蚀仅轻微缩小其边缘,后续膨胀可精准恢复,几乎不改变目标的整体形态。
1.2.3 示例(二值图像)
原始图像:包含一个大的白色圆形目标 + 3 个小的白色噪声点。
腐蚀后:小噪声点被完全消除,大圆形目标边缘缩小(直径减小)。
膨胀后:大圆形目标恢复原始直径,小噪声点因已被腐蚀消失,无法恢复。
最终效果:仅保留干净的大圆形目标,噪声被去除。
1.3 闭运算(Closing):先膨胀,后腐蚀
1.3.1 定义
闭运算 = 膨胀(Dilation)→ 腐蚀(Erosion)先通过膨胀填充前景目标内部的小背景孔洞,再通过腐蚀恢复目标的原始尺寸(已填充的孔洞不会重新出现)。
1.3.2 核心作用
填充小的背景孔洞:比如前景目标内部的黑色小点(孔洞),会被膨胀填充为白色,后续腐蚀仅恢复目标边缘,孔洞保持填充状态。
连接断裂的前景目标:若前景目标有轻微断裂(小缝隙),膨胀会填补缝隙使目标连接,后续腐蚀可让目标边缘恢复平滑,保持连接状态。
保留大目标的整体结构:对大的前景目标,膨胀仅填充内部小孔洞,后续腐蚀可精准恢复目标边缘,不改变目标的外部形态。
1.3.3 示例(二值图像)
原始图像:包含一个大的白色圆形目标(内部有 2 个小的黑色孔洞)。
膨胀后:内部的小黑洞洞被填充为白色,大圆形目标边缘轻微扩大。
腐蚀后:大圆形目标恢复原始直径,内部已填充的孔洞保持白色(不会重新变为黑色)。
最终效果:大圆形目标内部无孔洞,形态干净完整。
1.4 开运算 vs 闭运算:关键差异对比
| 维度 | 开运算(Opening) | 闭运算(Closing) |
| 操作顺序 | 腐蚀 → 膨胀 | 膨胀 → 腐蚀 |
| 核心目标 | 处理「前景噪声」(白色小点) | 处理「背景孔洞」(黑色小点) |
| 对目标的影响 | 消除小前景,分离粘连目标 | 填充小背景孔洞,连接断裂目标 |
| 结构元素依赖 | 结构元素尺寸需略大于噪声尺寸 | 结构元素尺寸需略大于孔洞尺寸 |
| 典型应用场景 | 去除毛发、斑点等前景噪声 | 填充文字内部孔洞、修复目标裂缝 |
1.5 代码实现(OpenCV-Python)
OpenCV 提供 cv2.morphologyEx() 函数统一实现开 / 闭运算,通过 op 参数指定操作类型:
开运算:op=cv2.MORPH_OPEN
闭运算:op=cv2.MORPH_CLOSE
import cv2
import numpy as np# 1. 读取二值图像(以灰度图读取后,用阈值处理转为二值图)
img = cv2.imread("binary_image.png", 0) # 0表示灰度模式读取
_, binary_img = cv2.threshold(img, 127, 255, cv2.THRESH_BINARY) # 大于127为白(255),小于为黑(0)# 2. 定义结构元素(3×3正方形,可根据需求调整尺寸)
kernel = np.ones((3, 3), np.uint8)# 3. 执行开运算(去除前景噪声)
opening = cv2.morphologyEx(binary_img, cv2.MORPH_OPEN, kernel)# 4. 执行闭运算(填充背景孔洞)
closing = cv2.morphologyEx(binary_img, cv2.MORPH_CLOSE, kernel)# 5. 显示结果
cv2.imshow("Original Binary", binary_img)
cv2.imshow("Opening (Remove Noise)", opening)
cv2.imshow("Closing (Fill Holes)", closing)
cv2.waitKey(0)
cv2.destroyAllWindows()1.6 扩展:灰度图像的开 / 闭运算
开 / 闭运算同样适用于灰度图像,核心逻辑与二值图像一致,但操作对象变为像素的灰度值:
灰度开运算:先腐蚀(抑制亮的小噪声),后膨胀(恢复主体亮区域的灰度),可去除图像中的亮斑噪声。
灰度闭运算:先膨胀(填充暗的小孔洞),后腐蚀(恢复主体暗区域的灰度),可去除图像中的暗斑孔洞。
代码实现与二值图像类似,仅需省略 “阈值转换” 步骤,直接对灰度图操作即可。
2、梯度运算
在图像处理中,梯度运算(Gradient Operation) 是一种基于图像灰度变化的边缘检测方法,核心是通过计算像素值的变化率(梯度)来识别图像中物体的边缘(灰度突变区域)。
梯度本质上是一个向量,包含方向(灰度变化最剧烈的方向)和大小(灰度变化的强度)。在实际应用中,通常用梯度大小来表示边缘的明显程度(值越大,边缘越清晰)。
2.1 梯度运算的数学基础


2.2 常用梯度算子
在计算机中,图像是离散的像素矩阵,无法直接计算偏导数,因此需要用差分算子近似计算梯度。常用的梯度算子有:

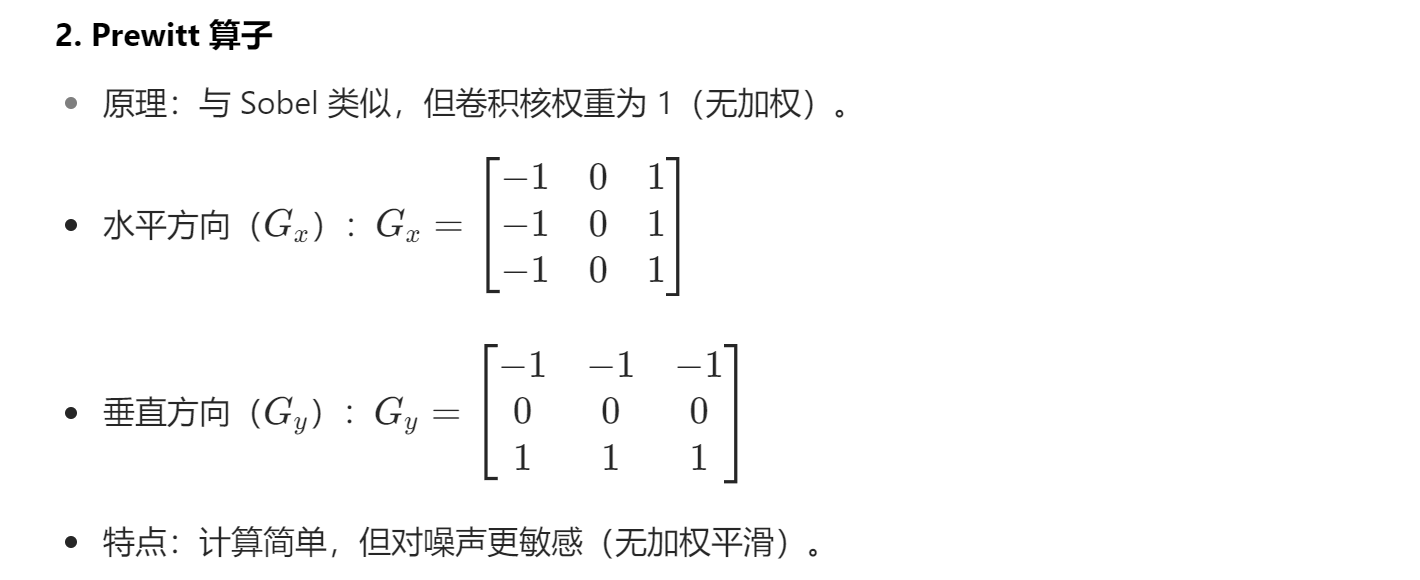

2.3 梯度运算的作用
边缘检测:梯度大小大的区域对应图像中物体的边缘(如物体轮廓、纹理边界)。
特征提取:边缘是图像的重要特征,可用于目标识别、图像分割等任务。
图像增强:通过突出梯度区域,增强图像的细节对比。
2.4 OpenCV 代码实现(Python)
OpenCV 提供 cv2.Sobel()、cv2.Laplacian() 等函数直接计算梯度,示例如下:
import cv2
import numpy as np
import matplotlib.pyplot as plt# 读取灰度图像
img = cv2.imread("image.jpg", 0) # 0表示灰度模式# 1. Sobel 梯度运算
# 计算x方向梯度(垂直边缘)
sobel_x = cv2.Sobel(img, cv2.CV_64F, 1, 0, ksize=3) # dx=1, dy=0(只算x方向)
sobel_x = cv2.convertScaleAbs(sobel_x) # 取绝对值并转为uint8# 计算y方向梯度(水平边缘)
sobel_y = cv2.Sobel(img, cv2.CV_64F, 0, 1, ksize=3) # dx=0, dy=1(只算y方向)
sobel_y = cv2.convertScaleAbs(sobel_y)# 合并x和y方向梯度(总边缘)
sobel_xy = cv2.addWeighted(sobel_x, 0.5, sobel_y, 0.5, 0)# 2. Laplacian 梯度运算(需先平滑以减少噪声)
blurred = cv2.GaussianBlur(img, (3, 3), 0) # 高斯模糊降噪
laplacian = cv2.Laplacian(blurred, cv2.CV_64F, ksize=3)
laplacian = cv2.convertScaleAbs(laplacian)# 显示结果
plt.figure(figsize=(12, 8))
plt.subplot(221), plt.imshow(img, cmap='gray'), plt.title('Original')
plt.subplot(222), plt.imshow(sobel_x, cmap='gray'), plt.title('Sobel X (Vertical Edges)')
plt.subplot(223), plt.imshow(sobel_y, cmap='gray'), plt.title('Sobel Y (Horizontal Edges)')
plt.subplot(224), plt.imshow(sobel_xy, cmap='gray'), plt.title('Sobel XY (Total Edges)')
plt.show()2.5 注意事项
数据类型:梯度计算可能产生负值(如边缘两侧的灰度差),需用 cv2.CV_64F 保留负值,再通过 convertScaleAbs 转为正数。
噪声影响:梯度对噪声敏感,实际应用中通常先对图像进行平滑处理(如高斯模糊)。
算子选择:Sobel 算子因抗噪声能力强,是最常用的梯度计算方法;Laplacian 适合检测细微边缘,但需配合降噪使用。
3、礼帽与黑帽
礼帽 = 原始输入-开运算结果
黑帽 = 闭运算-原始输入
3.1 礼帽运算:
定义:礼帽运算也叫顶帽运算,是原始图像与开运算结果的差值,数学表达式为:礼帽图像 = 原始图像 - 开运算图像。
作用:开运算可以消除暗背景下的高亮区域,因此礼帽运算能够突出原图像中灰度较亮的区域,通常用于检测图像中的小亮斑点或小亮物体。
应用:在信用卡数字识别中,可通过礼帽运算分离出数字字体,便于后续的轮廓提取和字符识别。
3.2 黑帽运算:
定义:黑帽运算是闭运算结果与原始图像的差值,数学表达式为:黑帽图像 = 闭运算图像 - 原始图像。
作用:闭运算可以删除亮背景下的暗区域,所以黑帽运算能够突出原图像中灰度较暗的区域,常用于检测图像中的小暗斑点或小暗物体。
应用:在图像二值化后,黑帽运算可用于去除孤立点,也可用于检测图像中的阴影区域等。
