模式识别与机器学习课程笔记（6）：人工神经网络

人工神经网络基础知识

一、人工神经网络基础知识

人工神经网络（ANN）是模拟生物神经系统的计算模型，核心是通过 “神经元”的互联 实现非线性映射，解决线性模型无法处理的复杂问题（如图像识别、自然语言理解）。

1.1 人工神经网络（ANN）历史：三起两落的发展之路

ANN 的发展并非一帆风顺，经历了三次关键浪潮，每次低谷都为后续突破积累了理论基础：

• 第一阶段：1940s-1960s（起步与早期发展）

  • 1943 年：M-P 模型（神经元数学化的开端）
    McCulloch 和 Pitts 首次用数学公式描述生物神经元：
    $y=f\left({\sum }_{i=1}^n{w}_i{x}_i-\theta \right)$
    其中$x_i$是输入信号，$w_i$是连接权重，$\theta$是阈值，$f$是激活函数（当时为阶跃函数）。
    意义：将“神经元”从生物学概念转化为可计算的数学模型，奠定 ANN 的理论基石。
  • 1949 年：Hebb 学习规则（学习机制的启蒙）
    Hebb 在《The Organization of Behavior》中提出：“同时激活的神经元之间的连接会增强”（即“fire together, wire together”）。
    数学表达：$w_{ij}=w_{ij}+\eta x_i{y}_j$（$\eta$为学习率），这是最早的神经网络学习算法，为后续监督学习提供思路。
  • 1958 年：感知机（首个可训练的 ANN 模型）
    Rosenblatt 提出感知机模型，本质是单层线性分类器，能通过梯度下降最小化分类误差。
    局限：仅能处理线性可分问题（如“与”“或”运算），无法解决“异或（XOR）”这类非线性问题。
  • 1960 年：Adaline 与 Delta 规则（优化感知机）
    Widrow 和 Hoff 提出 Adaline（自适应线性神经元），将输出从“离散分类”改为“连续值”，并提出 Delta 规则（最小均方误差 MSE），为后续 BP 算法的误差反向传播埋下伏笔。
  • 1969 年：《Perceptrons》与第一次低谷
    Minsky 和 Papert 在书中严格证明：单层神经网络无法解决非线性问题，而多层网络的训练算法尚无有效方案。
    这一结论直接导致 ANN 研究资金削减，进入长达十余年的“寒冬”。

• 第二阶段：1980s-1990s（复兴与挑战）

  • 1982 年：Hopfield 网络（递归网络的突破）
    物理学家 Hopfield 提出递归网络模型，利用能量函数实现“联想记忆”（如从模糊图像恢复清晰图像）和优化计算（如旅行商问题 TSP），证明了 ANN 在非监督学习和优化领域的价值。
  • 1974-1986 年：BP 算法的“重生”
    1974 年 Werbos 首次提出反向传播（BP）算法，但未受重视；1986 年 Rumelhart 等人在《Parallel Distributed Processing》中重新发表该算法，证明 BP 能有效训练多层神经网络，解决了 Minsky 指出的“多层训练难题”。
    意义：直接推动 ANN 复兴，多层感知器（MLP）开始广泛应用于语音识别、手写体识别等领域。
  • 1987 年：ICNN 会议（学科规范化）
    IEEE 召开第一届神经网络国际会议（ICNN），标志着 ANN 成为独立学科，学术研究和工业应用进入爆发期。
  • 1990s 初：第二次低谷（统计学习的冲击）
    随着支持向量机（SVM）、决策树等统计学习模型的兴起，ANN 的短板凸显：
    • 理论基础薄弱（如通用近似定理无法指导网络设计）；
    • 训练不稳定（易陷入局部最优、梯度消失）；
    • 数据需求大（小样本场景下性能不如 SVM）。
      ANN 研究再次降温，直至 2006 年深度学习的出现。

• 第三阶段：2000s-2010s（深度学习崛起）

  • 2006 年：深度信念网络（DBN）与“预训练”
    Hinton 提出 DBN 模型，通过“逐层预训练 + 全局微调”策略，解决了深度网络（多层隐藏层）的梯度消失问题，首次证明“深度”比“宽度”更重要。
  • 2012 年：AlexNet 与 CNN 革命
    Hinton 团队的 AlexNet 在 ImageNet 竞赛中，以 15.3% 的 Top-5 误差远超第二名（26.2%），核心创新包括：
    • 使用 ReLU 激活函数替代 sigmoid，解决梯度消失；
    • 用 GPU 加速训练（当时首次将 GPU 用于深度学习）；
    • 引入重叠池化、局部响应归一化（LRN）。
      意义：深度学习正式“出圈”，CNN 成为计算机视觉的主流模型。
  • 2010s：全面爆发（大数据 + 算力 + 算法）
    云计算（AWS、阿里云）提供大规模算力，大数据时代积累海量标注数据，加上 Adam 优化器、Batch Normalization 等算法改进，深度学习在 NLP（BERT）、语音（DeepSpeech）、推荐系统等领域全面突破，ANN 进入“深度学习时代”。

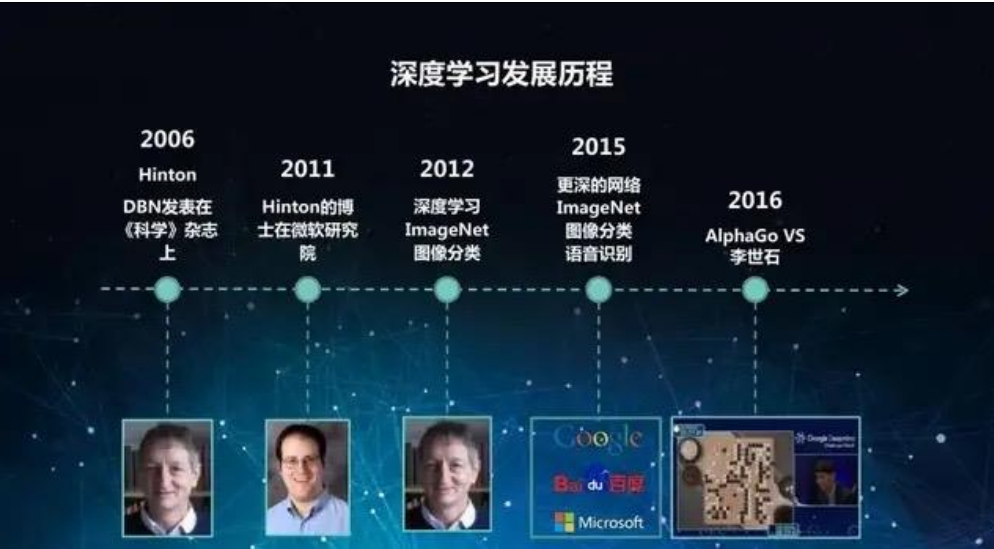
1.2 深度学习发展历程

下图梳理了深度学习从 ANN 到 Transformer 的核心里程碑：

1.3 生物神经系统简介（ANN 的仿生来源）

ANN 的设计灵感源于人脑，理解生物神经系统能更好地把握 ANN 的本质：

1. 生物神经元结构与工作方式
   生物神经元由细胞体、树突、轴突、突触四部分组成，工作流程如下：

   • 树突接收来自其他神经元的化学信号（神经递质）；
   • 细胞体将信号整合为电信号，若超过阈值则“激活”；
   • 轴突将电信号传递到突触，通过神经递质传递给下一个神经元。

2. 规模与传导速度

   • 规模：人脑约含 860 亿个神经元，每个神经元连接 1000-10000 个其他神经元，总连接数超$10^{14}$，形成复杂的并行网络。
   • 传导速度：生物信号传导速度约 1-100 m/s（远慢于电子信号的$3\times 10^8$ m/s），但通过并行计算（多神经元同时工作）实现高效信息处理。

3. 与 ANN 的差异
   ANN 是生物神经系统的“简化版”——人工神经元仅模拟“信号加权求和 + 激活”，而生物神经元的突触可塑性（学习能力）、容错性（部分神经元受损不影响整体）仍远超现有 ANN。

1.4 人工神经网络模型（以前馈网络为例）

前馈神经网络（多层感知器 MLP）是最基础的 ANN 模型，结构分为输入层、隐藏层、输出层，信号仅从输入向输出单向传播（无反馈）：

• 输入层：接收原始数据（如图像的像素值、文本的嵌入向量），神经元数量 = 特征维度（如 MNIST 图像输入层为 784 个神经元，对应 28×28 像素）。
• 隐藏层：对输入特征进行非线性变换，层数和神经元数量需根据任务调整（如简单分类任务 1-2 层隐藏层即可，复杂任务需更多层）。
• 输出层：输出模型结果（如分类任务输出类别概率，回归任务输出连续值），神经元数量 = 任务目标数（如二分类输出层 1 个神经元，10 分类 10 个神经元）。

1.5 常用激活函数（引入非线性的核心）

激活函数的作用是为网络引入非线性——若无激活函数，多层网络等价于单层线性网络，无法拟合非线性问题（如异或）。以下是主流激活函数的对比：

函数名称	公式	图像特点	优缺点	适用场景
符号函数	$f(x)=\{\begin{array}{ll}1& x\ge 0\\ -1& x<0\end{array}$	二值输出，阶跃形	优点：简单；缺点：无梯度，无法训练	早期感知机（已淘汰）
逻辑 sigmoid	$f(x)=\frac{1}{1+e^{-x}}$	输出∈(0,1)，S 形	优点：输出可解释为概率；缺点：梯度消失	二分类输出层
双曲正切 tanh	$f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$	输出∈(-1,1)，S 形	优点：零中心化；缺点：仍有梯度消失	早期隐藏层（已被 ReLU 替代）
ReLU	$f(x)=\max (0,x)$	x≥0 时线性，x<0 时为 0	优点：缓解梯度消失，计算快；缺点：死亡神经元	现代网络隐藏层（最常用）
Leaky ReLU	$f(x)=\{\begin{array}{ll}x& x\ge 0\\ \alpha x& x<0\end{array}$（α≈0.01）	x<0 时非零，微小斜率	优点：解决死亡神经元；缺点：α 需调参	隐藏层（替代 ReLU 的选择）
Mish	$f(x)=x\cdot \tanh (\ln (1+e^x))$	平滑曲线，无尖锐拐点	优点：性能优于 ReLU，鲁棒性强；缺点：计算稍慢	复杂任务（如目标检测、GAN）

激活函数可视化代码（Python）

import numpy as np
import matplotlib.pyplot as plt# 定义激活函数
def sigmoid(x):return 1 / (1 + np.exp(-x))def tanh(x):return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))def relu(x):return np.maximum(0, x)def leaky_relu(x, alpha=0.01):return np.where(x >= 0, x, alpha * x)def mish(x):return x * tanh(np.log(1 + np.exp(x)))# 生成x值
x = np.linspace(-5, 5, 1000)# 绘图
plt.figure(figsize=(12, 8))
plt.subplot(2, 3, 1)
plt.plot(x, np.where(x >= 0, 1, -1))
plt.title('符号函数')
plt.grid(True)plt.subplot(2, 3, 2)
plt.plot(x, sigmoid(x))
plt.title('Sigmoid')
plt.grid(True)plt.subplot(2, 3, 3)
plt.plot(x, tanh(x))
plt.title('Tanh')
plt.grid(True)plt.subplot(2, 3, 4)
plt.plot(x, relu(x))
plt.title('ReLU')
plt.grid(True)plt.subplot(2, 3, 5)
plt.plot(x, leaky_relu(x))
plt.title('Leaky ReLU')
plt.grid(True)plt.subplot(2, 3, 6)
plt.plot(x, mish(x))
plt.title('Mish')
plt.grid(True)plt.tight_layout()
plt.show()

二、人工神经网络类型（按结构分类）

根据网络中信号的传播方向和结构特点，ANN 可分为四大类：

2.1 前馈网络（Feedforward Network）

• 定义：信号从输入层→隐藏层→输出层单向传播，无反馈回路，结构最简单。
• 核心特点：无记忆性（当前输出仅依赖当前输入，与历史输入无关）。
• 典型模型：多层感知器（MLP）、卷积神经网络（CNN）。
• 应用场景：静态数据处理（如图像分类、表格数据回归）。

2.2 记忆网络（反馈网络 / 递归网络）

• 定义：包含反馈回路（隐藏层输出可反馈到自身或前层），能利用历史信息。
• 核心特点：有记忆性（当前输出依赖当前输入 + 历史输入）。
• 典型模型：循环神经网络（RNN）、长短期记忆网络（LSTM）、门控循环单元（GRU）。
• 应用场景：时序数据处理（如文本翻译、语音识别、股票预测）。

2.3 图网络（Graph Neural Network, GNN）

• 定义：处理图结构数据（如社交网络、分子结构、知识图谱），每个节点代表一个实体，边代表实体间的关系。
• 核心特点：能捕捉节点间的依赖关系（如社交网络中“朋友的朋友”的影响）。
• 典型模型：图卷积网络（GCN）、图注意力网络（GAT）。
• 应用场景：节点分类（如判断社交网络中用户是否为 spam）、链路预测（如预测未来是否会产生新的社交关系）。

2.4 卷积神经网络（CNN）

• 定义：专为空间数据（如图像、视频）设计的前馈网络，通过“卷积层”提取局部特征。
• 核心特点：局部感受野、权值共享（减少参数数量，防过拟合）。
• 应用场景：图像识别（如人脸识别）、目标检测（如自动驾驶中的障碍物检测）、图像生成（如 GAN）。

三、前馈神经网络（多层感知器 MLP）深度解析

MLP 是最基础的前馈网络，理解 MLP 是掌握复杂网络（如 CNN、Transformer）的关键。

3.1 能实现“与”运算的两层 MLP（实例）

• “与”运算的逻辑规则：输入$(x_1,x_2)$为 (0,0)→0，(0,1)→0，(1,0)→0，(1,1)→1。
  用两层 MLP 实现（输入层 2 个神经元，输出层 1 个神经元，无隐藏层）：

• 网络参数设置：
  权重$w_1=1,w_2=1$（输入对输出的贡献）；
  偏置$b=-1.5$（调整激活阈值）；
  激活函数：sigmoid（输出概率，取 0.5 为阈值）。

• 计算过程：
  输出$y=\text{sigmoid}(w_1{x}_1+w_2{x}_2+b)$

  • 输入 (0,0)：$y=\text{sigmoid}(0+0-1.5)\approx 0.18<0.5$ → 输出 0；
  • 输入 (1,1)：$y=\text{sigmoid}(1+1-1.5)\approx 0.82>0.5$ → 输出 1；
    其余输入计算结果均 <0.5，完美实现“与”运算。

  同理，通过调整权重和偏置，MLP 可实现“或”“非”运算；若增加隐藏层，可实现“异或”运算（解决单层网络的局限）。

3.2 通用近似定理（MLP 的理论基础）

• 定理内容：若激活函数是连续、有界、非多项式的（如 ReLU、sigmoid），则仅需 1 个隐藏层、足够多的神经元，MLP 能以任意精度近似定义在紧致集上的连续函数。
• 通俗理解：只要隐藏层神经元数量足够，MLP 可以拟合任何复杂的非线性关系（如图像中的物体特征、文本中的语义关联）。
• 注意事项：
  1. “足够多”无明确公式，需根据任务通过实验调整（如从 128、256 个神经元开始尝试）；
  2. 隐藏层过多（如深度超过 10 层）可能导致过拟合或训练困难，需结合正则化技巧。

四、网络训练（从“参数随机”到“参数最优”）

网络训练的核心是寻找最优权重和偏置，使模型输出与真实标签的误差最小化。

4.1 前馈网络函数表达式（数学定义）

设 MLP 有$L$层（输入层为第 0 层，输出层为第$L$层），则第$l$层的输出为：
$a^{(l)}=f^{(l)}\left(W^{(l)}{a}^{(l-1)}+b^{(l)}\right)$

其中：

• $a^{(l)}$：第$l$层的输出（激活值），$a^{(0)}$为输入特征；
• $W^{(l)}$：第$l$层的权重矩阵，维度为（第$l$层神经元数 × 第$l-1$层神经元数）；
• $b^{(l)}$：第$l$层的偏置向量，维度为（第$l$层神经元数 × 1）；
• $f^{(l)}$：第$l$层的激活函数（如隐藏层用 ReLU，输出层用 sigmoid）。

4.2 网络训练的目标函数（误差度量）

目标函数（损失函数）用于衡量模型输出与真实标签的差异，常见类型如下：

任务类型	目标函数	公式（单样本）	适用场景
回归	均方误差（MSE）	$\mathcal{L}=\frac{1}{2}|y-\hat{y}{|}^2$	预测连续值（如房价、温度）
二分类	二元交叉熵（BCE）	$\mathcal{L}=-y\ln \hat{y}-(1-y)\ln (1-\hat{y})$	输出 0/1 类别概率
多分类	类别交叉熵（CCE）	$\mathcal{L}=-{\sum }_{c=1}^C{y}_c\ln {\hat{y}}_c$	输出多类别概率（如 10 分类）

批量损失：对所有样本的损失取平均，即$\mathcal{J}(W,b)=\frac{1}{N}{\sum }_{i=1}^N\mathcal{L}(y_i,{\hat{y}}_i)$（$N$为样本数）。

4.3 梯度下降法（优化核心算法）

梯度下降法是最小化目标函数$\mathcal{J}(W,b)$的核心算法，基本思想是沿梯度负方向更新参数（梯度是函数上升最快的方向，负梯度即下降最快的方向）。

1. 参数更新公式

$W^{(l)}=W^{(l)}-\eta \cdot \frac{\partial \mathcal{J}}{\partial W^{(l)}}$
$b^{(l)}=b^{(l)}-\eta \cdot \frac{\partial \mathcal{J}}{\partial b^{(l)}}$

其中：

• $\eta$：学习率（步长），控制每次参数更新的幅度（常用值：0.001、0.01、0.1）；
• $\frac{\partial \mathcal{J}}{\partial W^{(l)}}$：目标函数对$W^{(l)}$的梯度（需通过反向传播计算）。

2. 梯度下降的三种变体

变体类型	计算方式	优点	缺点
批量梯度下降（BGD）	用全部样本计算梯度	梯度稳定，收敛到全局最优	计算量大，不适合大数据集
随机梯度下降（SGD）	用单个样本计算梯度	计算快，适合大数据集	梯度震荡，易陷入局部最优
小批量梯度下降（MBGD）	用$k$个样本（批量大小）计算梯度	平衡稳定性和计算效率	需调整批量大小$k$（常用值：32、64、128）

实际训练中几乎都用 MBGD，如 PyTorch 的DataLoader默认按批次加载数据。

4.4 网络误差函数选择的经验

1. 回归任务优先用 MSE：若数据含异常值，可改用 MAE（平均绝对误差），因为 MSE 对异常值更敏感（平方放大误差）。
2. 分类任务必须用交叉熵：若用 MSE，输出层激活函数（如 sigmoid）的梯度会非常小（梯度消失），导致训练缓慢；交叉熵能与 sigmoid/tanh 配合，缓解梯度消失。
3. 类别不平衡用加权交叉熵：若正样本占比仅 10%，可设置权重$w_{\text{正}}=9,w_{\text{负}}=1$，避免模型偏向多数类（负样本）。

五、误差反向传播算法（BP 算法：训练 MLP 的“引擎”）

BP 算法是计算目标函数对各层参数梯度的高效方法，核心是链式法则（从输出层反向计算各层误差，再求梯度）。

5.1 BP 算法的核心步骤（以 MLP 为例）

假设网络有输入层、1 个隐藏层、输出层，激活函数分别为 ReLU（隐藏层）和 sigmoid（输出层），目标函数为 MSE。

步骤 1：前馈计算（求各层输出）

• 隐藏层输出：$a^{(1)}=\text{ReLU}(W^{(1)}{a}^{(0)}+b^{(1)})$
• 输出层输出：$\hat{y}=\text{sigmoid}(W^{(2)}{a}^{(1)}+b^{(2)})$

步骤 2：反向计算误差（从输出层到隐藏层）

• 输出层误差（衡量输出与真实标签的差异）：
  ${\delta }^{(2)}=(\hat{y}-y)\cdot \hat{y}\cdot (1-\hat{y})$
  （$\hat{y}\cdot (1-\hat{y})$是 sigmoid 的导数，即$\frac{\partial f^{(2)}}{\partial z^{(2)}}$，$z^{(2)}=W^{(2)}{a}^{(1)}+b^{(2)}$）

• 隐藏层误差（将输出层误差反向传播到隐藏层）：
  ${\delta }^{(1)}=(W^{(2)T}{\delta }^{(2)})\cdot \mathbb{I}(a^{(1)}>0)$
  （$\mathbb{I}(a^{(1)}>0)$是 ReLU 的导数，即$a^{(1)}>0$时为 1，否则为 0；$W^{(2)T}$是$W^{(2)}$的转置）

步骤 3：计算梯度并更新参数

• 权重梯度：
  $\frac{\partial \mathcal{J}}{\partial W^{(2)}}={\delta }^{(2)}\cdot a^{(1)T}$
  $\frac{\partial \mathcal{J}}{\partial W^{(1)}}={\delta }^{(1)}\cdot a^{(0)T}$

• 偏置梯度：
  $\frac{\partial \mathcal{J}}{\partial b^{(2)}}={\delta }^{(2)}$
  $\frac{\partial \mathcal{J}}{\partial b^{(1)}}={\delta }^{(1)}$

• 参数更新（用小批量梯度下降）：
  对批量内所有样本的梯度取平均，再按梯度下降公式更新$W^{(1)},b^{(1)},W^{(2)},b^{(2)}$。

5.2 BP 网络学习的基础

• 误差反向传播的本质：通过链式法则，将输出层的误差“分摊”到各层参数，指导参数更新。
• 梯度消失问题：若网络层数过多（如 > 5 层），隐藏层误差${\delta }^{(l)}$会随层数增加而趋近于 0（因为 sigmoid 导数最大仅 0.25，多层相乘后梯度衰减），导致浅层参数无法更新。
• 解决方法：用 ReLU 激活函数（导数为 1，无衰减）、Batch Normalization（标准化激活值，稳定梯度）。

六、主流神经网络简介（CNN/RNN/Transformer）

除了 MLP，以下三种网络是当前深度学习的核心，需重点掌握：

6.1 CNN 简介（计算机视觉的“利器”）

1. 核心创新：解决 MLP 处理图像的痛点

MLP 处理图像时存在两个问题：

• 参数爆炸：如 28×28 图像输入 MLP，隐藏层 1000 个神经元，权重数 = 784×1000=78.4 万，而 CNN 通过“权值共享”大幅减少参数；
• 忽略空间信息：MLP 将图像展平为向量，丢失像素间的位置关系（如“猫的眼睛在鼻子上方”），而 CNN 通过“局部感受野”捕捉空间特征。

2. 核心层与作用

层类型	作用	关键参数
卷积层（Conv）	提取局部特征（如边缘、纹理、形状）	卷积核大小（3×3 常用）、步长、填充
池化层（Pool）	降维（减少参数）、防过拟合	池化大小（2×2 常用）、最大 / 平均池化
全连接层（FC）	将卷积层提取的特征映射到类别空间	神经元数量

3. 典型模型与应用场景

• 典型模型：LeNet-5（首个 CNN）、AlexNet（深度学习革命）、ResNet（解决深度梯度消失）；
• 应用场景：图像分类（ResNet）、目标检测（YOLO）、图像分割（U-Net）。

6.2 RNN（时序数据的“专家”）

1. 核心结构：循环连接（捕捉历史信息）

RNN 的隐藏层有反馈回路，隐藏状态$h_t$不仅依赖当前输入$x_t$，还依赖上一时刻的隐藏状态$h_{t-1}$：
$h_t=f(W_h{h}_{t-1}+W_x{x}_t+b)$
$y_t=W_y{h}_t+b_y$

其中：

• $h_t$：$t$时刻的隐藏状态（记忆历史信息）；
• $y_t$：$t$时刻的输出。

2. 痛点：长序列依赖问题

当序列过长（如文本长度 > 50），RNN 的梯度会随时间步衰减（梯度消失）或爆炸，无法捕捉长距离依赖（如“我今天去了 [北京]，[那里] 的秋天很美”中“那里”指代“北京”）。

3. 改进模型与应用场景

• 改进模型：
  • LSTM：通过“输入门、遗忘门、输出门”控制信息的存入、遗忘和输出，解决长序列依赖（如 BERT 的编码器用 LSTM）；
  • GRU：简化 LSTM 的门控结构（仅更新门和重置门），计算更快，性能接近 LSTM（如语音识别常用 GRU）；
• 应用场景：文本生成（LSTM）、语音识别（GRU）、时序预测（RNN）。

6.3 Transformer（NLP 的“革命”，现扩展到 CV）

1. 核心创新：自注意力机制（Self-Attention）

Transformer 完全抛弃 RNN 的循环结构，用自注意力机制捕捉序列中任意两个元素的依赖关系（如文本中“猫”和“它”的指代关系），且支持并行计算（RNN 需按时间步串行计算，Transformer 可同时处理所有元素）。

2. 核心结构：Encoder-Decoder

• Encoder：将输入序列（如英文句子）编码为向量表示（含语义信息），由“多头注意力层 + 前馈网络”组成；
• Decoder：将 Encoder 的向量解码为输出序列（如中文句子），额外增加“掩码多头注意力层”（防止预测时看到未来的词）。

3. 典型模型与应用场景

• 典型模型：BERT（Encoder-only，用于文本理解）、GPT（Decoder-only，用于文本生成）、ViT（Vision Transformer，用于图像分类）；
• 应用场景：机器翻译（Transformer）、文本摘要（BERT）、图像分类（ViT）、大语言模型（GPT-4）。

七、网络优化注意事项

在实际训练网络时，常遇到过拟合、训练缓慢等问题，以下是关键优化技巧：

1. 数据预处理

• 归一化 / 标准化：将输入特征缩放到 [0,1] 或均值为 0、方差为 1（如 MNIST 像素归一化到 0-1），避免梯度爆炸；
• 数据增强：对图像（翻转、裁剪、旋转）、文本（同义词替换、随机插入）增加样本多样性，缓解过拟合。

2. 权重初始化

• 避免全零初始化：会导致所有神经元输出相同，无法学习；
• 推荐方法：Xavier 初始化（适合 sigmoid/tanh）、He 初始化（适合 ReLU），PyTorch 的nn.Linear默认用 He 初始化。

3. 学习率调整

• 初始学习率：从 0.001 开始尝试，太大导致震荡，太小收敛慢；
• 动态调整：用学习率调度器（如 StepLR、CosineAnnealingLR），训练后期减小学习率以稳定收敛。

4. 过拟合解决

• Dropout：训练时随机失活部分神经元（如隐藏层失活率 0.5），测试时恢复；
• 正则化：L1 正则化（权重稀疏）、L2 正则化（权重平滑），PyTorch 中通过weight_decay参数设置；
• 早停（Early Stopping）：监控验证集误差，若连续 5 个 epoch 无下降则停止训练，避免过拟合。

5. 批量大小选择

• 推荐值：32、64、128（需适配 GPU 内存，如 GPU 内存不足选 32）；
• 注意：批量大小太小会导致梯度震荡，太大可能陷入局部最优。

6. 激活函数与优化器选择

• 隐藏层：优先用 ReLU 或 Leaky ReLU；
• 输出层：二分类用 sigmoid，多分类用 softmax，回归用线性激活；
• 优化器：优先用 Adam（自适应学习率，收敛快），其次用 SGD + 动量（适合大规模数据）。

八、总结

本文从 ANN 的历史、基础模型、训练算法到主流网络，全面梳理了人工神经网络的核心知识。

关键结论

1. ANN 的发展是“理论突破 + 算力提升 + 数据积累”共同推动的结果；
2. MLP 是基础，CNN/RNN/Transformer 是针对特定任务的优化模型；
3. 实战中需结合数据预处理、正则化、学习率调整等技巧，才能训练出高性能模型；
4. 建议读者结合代码实战（如用 PyTorch 实现 MLP 和 CNN），加深对知识点的理解。后续可深入学习具体模型的源码（如 BERT、GPT），或探索多模态模型（如 CLIP）等前沿方向。