当前位置：首页 > news >正文

手搓二叉平衡搜索树--AVL树（万字长文/图文详解）

news 2025/10/15 7:58:04

////// 欢迎来到 aramae 的博客，愿 Bug 远离，好运常伴！ //////

博主的Gitee地址：阿拉美 (aramae) - Gitee.com

时代不会辜负长期主义者，愿每一个努力的人都能达到理想的彼岸。

一. AVL树前置知识

1. AVL树的概念

二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当于在顺序表中搜索元素，效率低下。

因此，两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。

一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：

它的左右子树都是AVL树
左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)

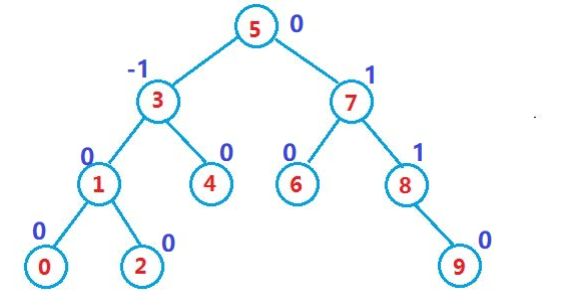
(默认平衡因子=右子树高度-左子树高度)

如果一棵二叉搜索树是高度平衡的，它就是AVL树。如果它有n个结点，其高度可保持在$O(log_2 n)$，搜索时间复杂度O($log_2 n$)

即AVL树是一棵高度平衡的二叉搜索树，它具有二叉搜索树的所有性质，且增加了自己的特性（引入平衡因子），这在后面的实现上会有所体现。

AVL树节点的定义

template<class K, class V> 
struct AVLTreeNode
{//三叉链: left right parentAVLTreeNode* _left;   // 该节点的左孩子 AVLTreeNode* _right;  // 该节点的右孩子 AVLTreeNode* _parent; // 该节点的双亲std::pair<K,V> _kv;	 // 键值对int _bf;              // 该节点的平衡因子 balance factorAVLTreeNode(const std::pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0){}
};

• 三叉链结构（左、右、父指针）
• 平衡因子记录高度差

2. 二叉搜索树基础

插入逻辑

while (cur)
{if (cur->_kv.first < kv.first)  // 向右查找else if (cur->_kv.first > kv.first) // 向左查找else return false; // 键已存在
}

保持二叉搜索树性质：左子树 < 根节点 < 右子树
时间复杂度：O(h)，h为树高

注：和二叉搜索树相关的内容在前面一篇文章已经做了详细讲解，感兴趣的可以看一下

3. AVL树核心概念

平衡因子定义

平衡因子 = 右子树高度 - 左子树高度（反过来也行）

我们这里统一使用右树-左树

int _bf; // balance factor = 右子树高度 - 左子树高度

合法值：-1, 0, 1

平衡条件：|bf| ≤ 1
bf ∈ {-2, -1, 0, 1, 2}

平衡因子更新规则

if (cur == parent->_left) parent->_bf--;
else parent->_bf++;

左子树插入：bf--
右子树插入：bf++

4. 旋转操作（核心算法）

四种不平衡情况

情况1：左左失衡 - 右单旋

右旋（RR 情况）

场景：节点的左子树比右子树高2，且左子树的左子树更高

        y                   x/ \                 / \x   T4      →       z   y/ \                 / \ / \z   T3              T1 T2 T3 T4/ \T1 T2

发生在左子树的左子树插入
解决方案：右旋

void RotateR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;parent->_left = curright;if (curright)curright->_parent = parent;Node* ppnode = parent->_parent;cur->_right = parent;if (ppnode == nullptr){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;}

情况2：右右失衡 - 左单旋

左旋（LL 情况）

场景：节点的右子树比左子树高2，且右子树的右子树更高

    y                   x/ \                 / \T1  x      →       y    z/ \            / \  / \T2  z          T1 T2 T3 T4/ \T3 T4

发生在右子树的右子树插入
解决方案：左旋

void RotateL(Node* parent){++_rotateCount;Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;if (curleft){curleft->_parent = parent;}cur->_left = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}parent->_bf = cur->_bf = 0;}

情况3：左右失衡 - 左右双旋

左右旋（LR 情况）

场景：节点的左子树比右子树高2，但左子树的右子树更高

    z                   z                 y/ \                 / \               / \x   T4  左旋x →     y   T4  右旋z →   x   z/ \                 / \               / \ / \
T1  y               x  T3             T1 T2 T3 T4/ \             / \T2 T3           T1 T2

发生在左子树的右子树插入
解决方案：先左旋后右旋

void RotateLR(Node* parent){Node* cur = parent->_left;Node* curright = cur->_right;int bf = curright->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 0){parent->_bf = 0;cur->_bf = 0;curright->_bf = 0;}else if (bf == -1){parent->_bf = 1;cur->_bf = 0;curright->_bf = 0;}else if (bf == 1){parent->_bf = 0;cur->_bf = -1;curright->_bf = 0;}else{return false;}}

情况4：右左失衡 - 右左双旋

右左旋（RL 情况）

场景：节点的右子树比左子树高2，但右子树的左子树更高

  z                 z                     y/ \               / \                   / \
T1  x   右旋x →   T1  y     左旋z →     z   x/ \               / \               / \ / \y  T4             T2  x             T1 T2 T3 T4/ \                   / \
T2 T3                 T3 T4

发生在右子树的左子树插入
解决方案：先右旋后左旋

void RotateRL(Node* parent){Node* cur = parent->_right;Node* curleft = cur->_left;int bf = curleft->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){cur->_bf = 0;curleft->_bf = 0;parent->_bf = 0;}else if (bf == 1){cur->_bf = 0;curleft->_bf = 0;parent->_bf = -1;}else if (bf == -1){cur->_bf = 1;curleft->_bf = 0;parent->_bf = 0;}else{assert(false);}}

5. 旋转操作实现细节

左旋步骤

保存相关节点指针
调整子树连接
更新父指针
处理根节点情况
重置平衡因子

双旋的特殊处理

双旋后需要根据子节点原始平衡因子调整

6. 平衡维护策略

向上回溯更新

终止条件

bf == 0：子树高度不变，停止向上更新
需要旋转：旋转后子树高度恢复，停止更新
到达根节点

二. AVL树的插入（详细分析+对应实现）

基本情况分析

AVL树就是在二叉搜索树的基础上引入了平衡因子，因此AVL树也可以看成是二叉搜索树。那么AVL树的插入过程可以分为两步：

按照二叉搜索树的方式插入新节点
调整节点的平衡因子

a. 更新父结点平衡因子

b. 根据父结点的平衡因子进行相应的操作

对于平衡因子

插入新结点后,首先可能会影响父结点的平衡因子,迭代往上,可能还会影响部分或全部(到根节点)祖先结点的平衡因子.

具体地说,即插入新结点后,需要根据父结点平衡因子的情况,决定是否继续往上对祖结点进行更新平衡因子,最多到达根结点.

平衡因子对应的操作

父结点平衡因子如何决定是否继续往上更新? 取决于更新后parent->_bf的值

1.若parent->_bf == 1 || parent->_bf == -1 ,说明插入前的父结点一定是左右子树高度相等,即_bf为0.新增结点后父结点所在子树高度一定发生变化,爷爷结点所在子树也可能发生变化,因此需要进行迭代更新祖先平衡因子.

不可能是2或-2变成1或-1,因为这是AVL树的插入,至少先保证是AVL树才能插入

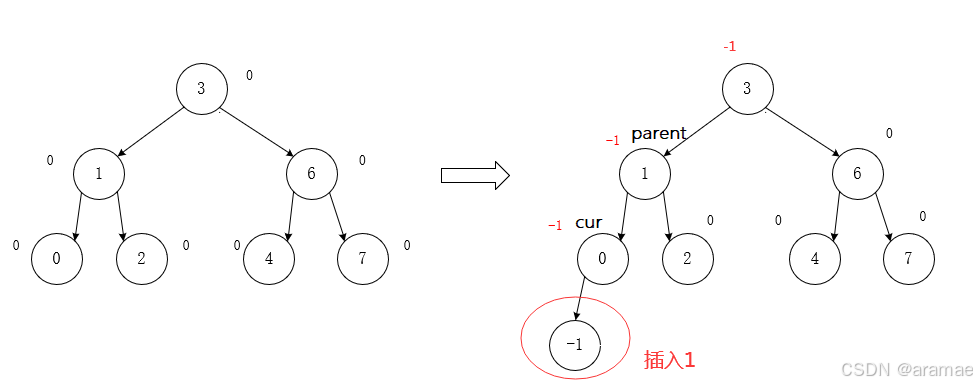
2. 若parent->_bf == 2 || parent->_bf == -2 ,说明插入前的父结点所在子树一边高一边低,之后新结点恰好插入到了高的一边,导致不平衡,需要做旋转操作,调整平衡.
3.parent->_bf == 0,插入后父结点的平衡因子平衡,说明原先父结点的左右子树是一边高一边低,然后插入刚好插到了低的一边,使其平衡.插入结束

旋转操作

分析需要旋转的情况

首先，要针对AVL子树，找出/抽象出可能发生旋转的情况。

一棵可能发生旋转的树至少高度差为1，即两个结点以上。（前提）

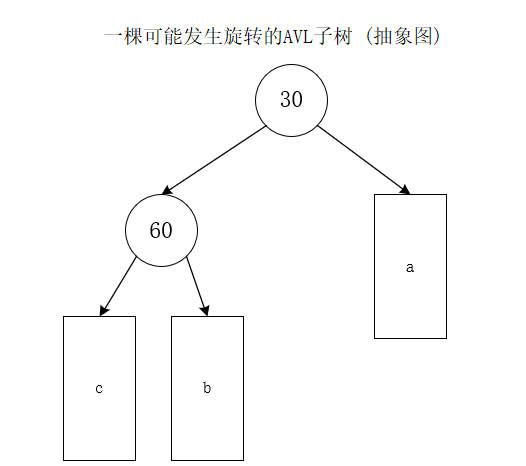
						（可能会发生旋转的子树至少两个结点以上）

其中a,b,c是三棵AVL子树

当子树高度h==0时,即a、b、c都为空树
当子树高度h==1时,a、b、c都是叶子结点
当子树高度h==2时,a、b、c分别有三种情况

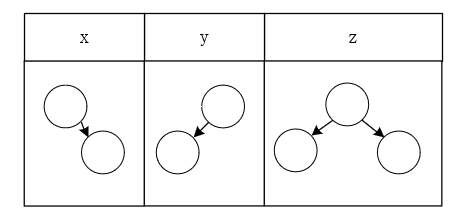
此时这个AVL子树有3*3*3=27种情况：a为x/y/z，b为x/y/z，c为x/y/z。
如此往下，还有更多的情况，但全部形状都可以用图中模型来代替。

以h==2为例，只有当b或c为z情况时，插入到b或c子树会影响到根结点（30），并使其发生旋转。
其他情况都无法使其发生旋转。因此，当前可以总结出2种需要旋转的情况：

c为z时，插到c中（左左）
b为z时，插到b中（左右）

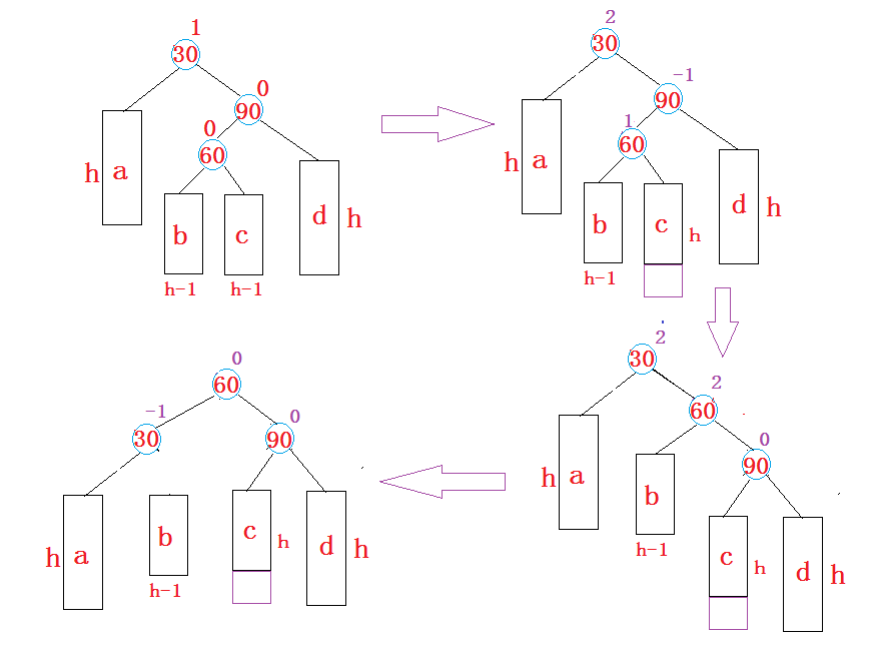
左左：较高的子树是左孩子（60）所在子树，插到左孩子（60）的左子树上（c）引发根（30）旋转的情况叫“左左”。

顺口：插在较高左子树的左孩子上。

同理，水平镜像翻转的AVL子树也同理

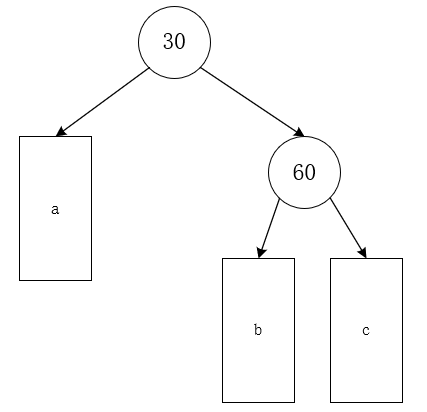
c为z时，插到c中（右右）
b为z时，插到b中（右左）

结论

合并起来总共4种需要旋转的情况，验证其他高度也同样如此。

其中插入b子树使30结点发生旋转的情况：a为x/y/z，b为z，c为x/y/z，总共3*3=9种

其中插入c子树使30结点发生旋转的情况：a为x/y/z，b为x/y/z，c为z，总共3*3=9种

特例的数量非常多，无法穷举。

4种旋转操方法与特征

新节点插入较高左子树的左侧---左左：右单旋
- 特征
  
  父：-2
  
  子：-1
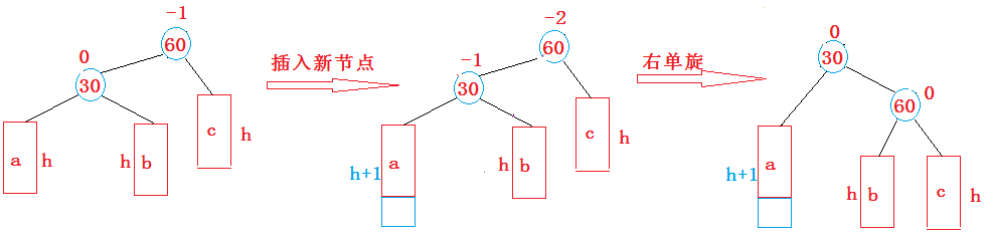
最左边高，旧根的左孩子变成新根，旧根成为新根的右孩子，同时领养新根的旧右孩子。

儿子上位 -- 儿子当根

右单旋（主角是儿子）：老爹在我的右上方，让老爹以我为轴，旋转到我的右下方
新节点插入较高右子树的右侧---右右：左单旋
- 特征
  
  父：2
  
  子：1
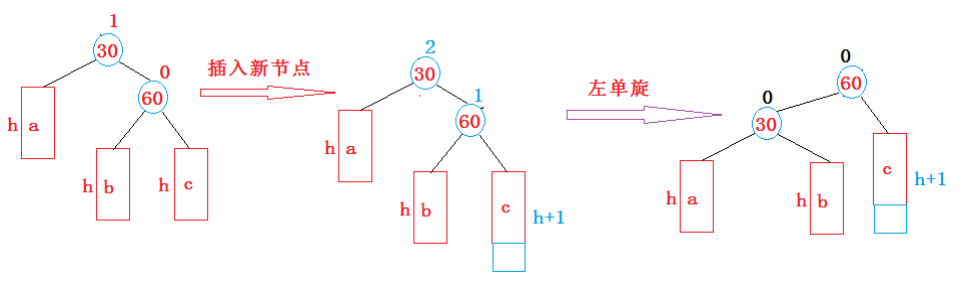
最右边高，旧根的右孩子变成新根，旧根成为新根的左孩子，同时领养新根的旧左孩子。
新节点插入较高左子树的右侧---左右：先左单旋再右单旋
- 特征
  
  父：-2
  
  子：1
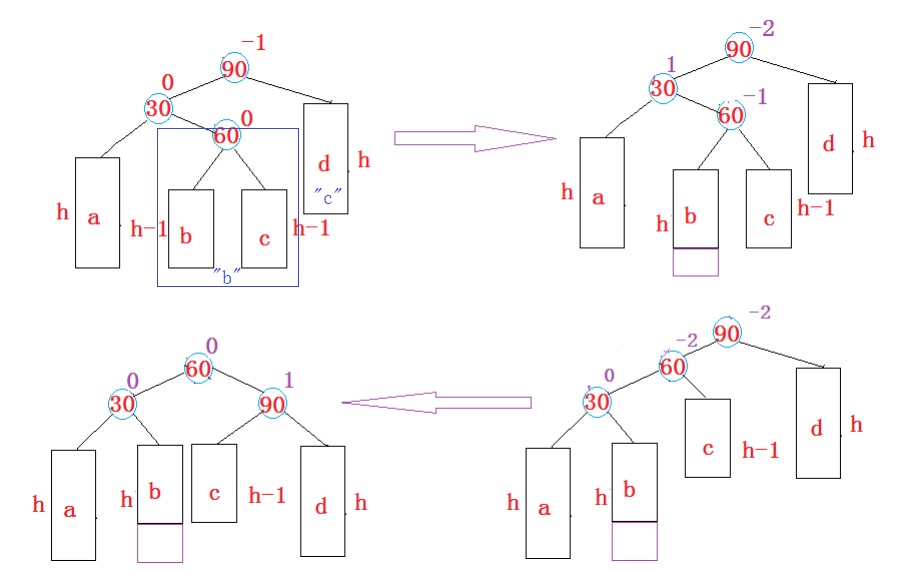
1. 旧根的左儿子的右孩子（简称右孙子）高：让右孙子成为旧根的左孩子，旧左孩子变成孙子的左孩子，同时领养孙子的左孩子。 -- 对右孙子做左旋操作
2. 右孙子成为旧根的新左儿子，再对新作儿子做右旋操作即可。
孙子上位 --- 孙子当根

感性描述：先左单旋再右单旋（孙子是主角）：我在孙子左边，我的老爹在孙子右边，然后让孙子的爹（我）左旋下来，孙子成为我的爹，我的旧爹成为孙子的爹；最后再让孙子的新爹右旋下来。

描述2：两次旋转分别用途： 1. 转化成标准单旋； 2.标准单旋
新节点插入较高右子树的左侧---右左：先右单旋再左单旋
- 特征
  
  父：2
  
  子：-1

总共4种旋转的情况：

右旋（左左）
左旋（右右)
先左旋再右旋（左右）
先右旋再左旋（右左）

简要图：

6种双旋平衡因子特征

容易发现单旋平衡因子都是0（高度差为0），而双旋平衡因子较为复杂，观察规律总结出一共6种情况。

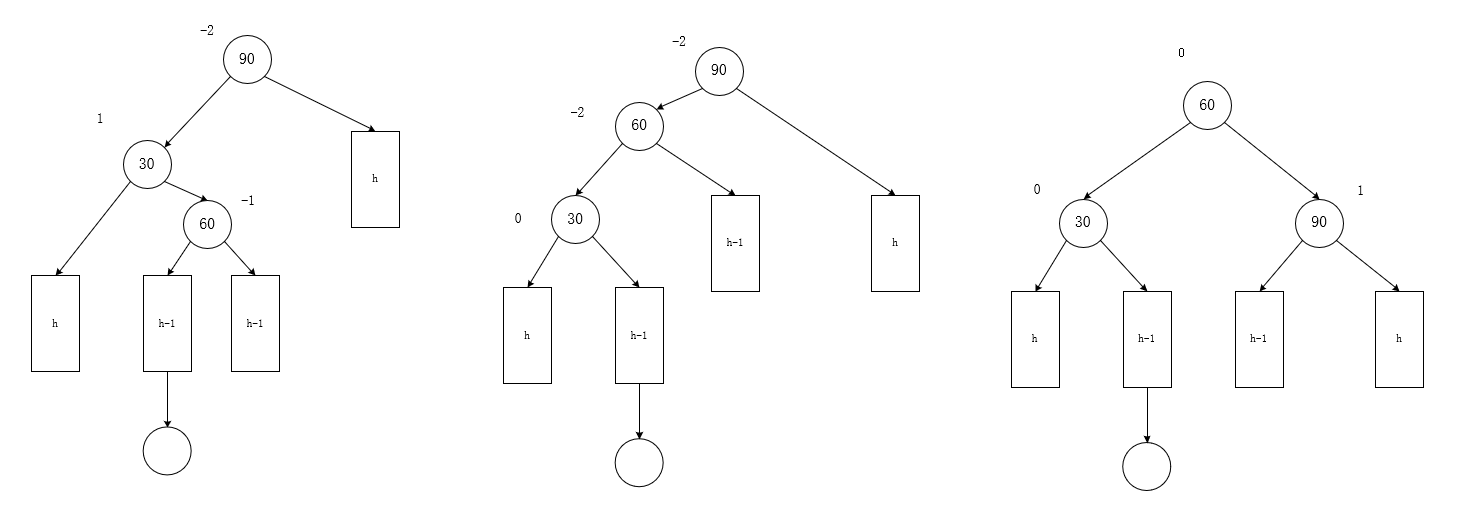
左右左（h>0)
- 旧（特征）
  
  孙：-1
- 新
  
  父：1
  
  子：0
  
  孙：0
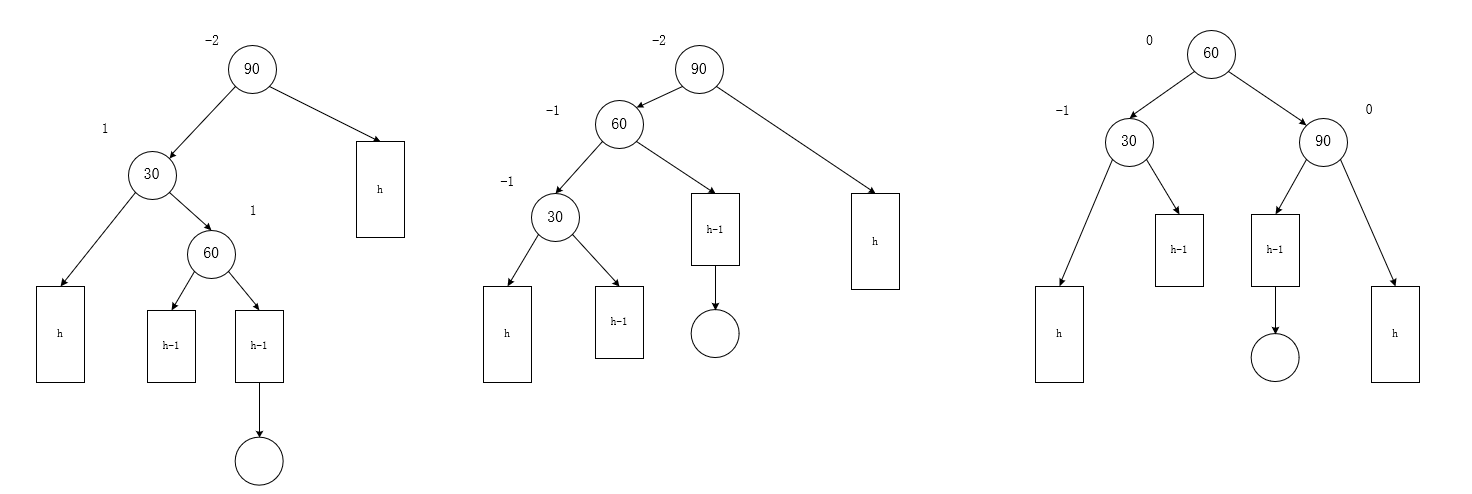
左右右(h>0)
- 旧（特征）
  
  孙：1
- 新
  
  父：0
  
  子：-1
  
  孙：0

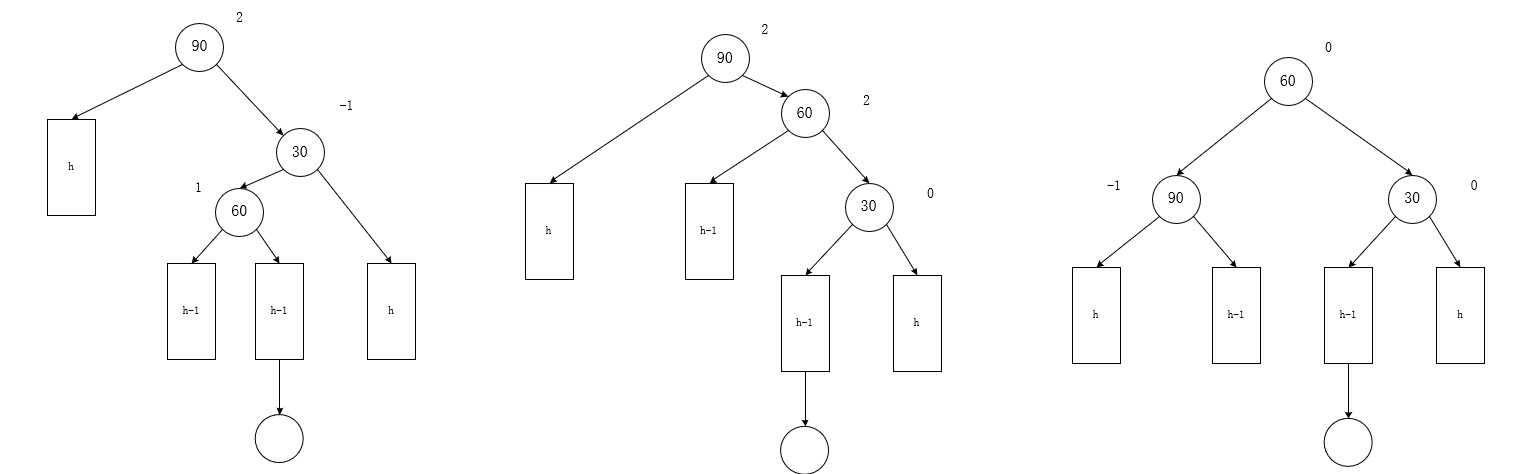
右左右（h>0）
- 旧（特征）
  
  孙：1
- 新
  
  父：-1
  
  子：0
  
  孙：0
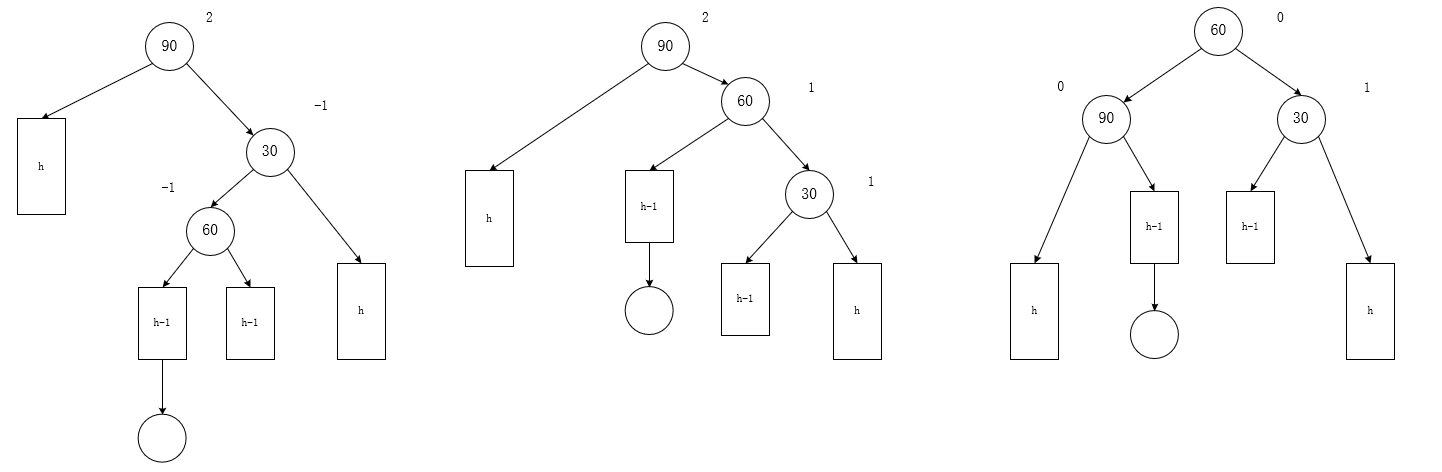
右左左（h>0）
- 旧（特征）
  
  孙：-1
- 新
  
  父：0
  
  子：1
  
  孙：0
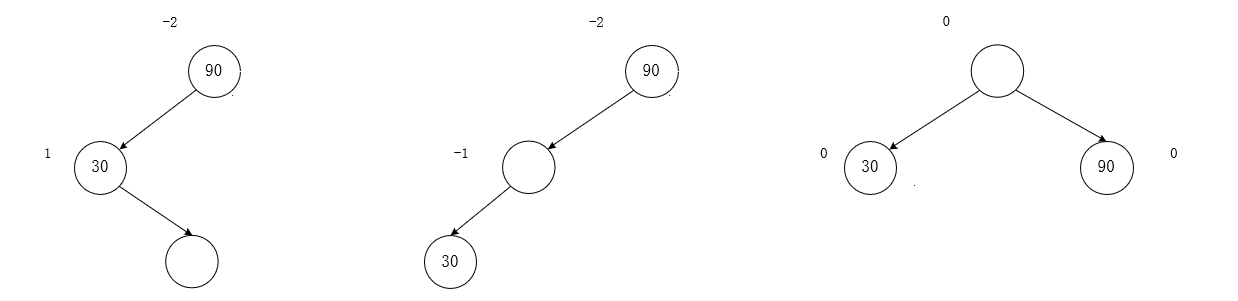
左右，特例（h==0)
- 旧（特征）
  
  孙：0
- 新
  
  父：0
  
  子：0
  
  孙：0
右左（h==0)，与5相同
- 旧（特征）
  
  孙：0
- 新
  
  父：0
  
  子：0
  
  孙：0

代码实现(汇总)

四种旋转实现

 //1. 右右void RotateL(Node* parent) {//. 记录爷爷(父亲的父亲)//. 我是父的右儿子(我是主角,儿子是新插入结点)//. 记录下我的左子树(托管)//  旋转(爷、父、子关系重新调整）//      成为爷爷的右儿子 (如果没有爷爷,则跳过;且说明父是根,更新我成为根)//      把我的左子树托管给父成为他的右孩子//      旧父成为我的左儿子,旧父的父更新成我//. 更新平衡因子//. 记录爷爷(父亲的父亲)//. 我是父的右儿子//. 记录下我的左子树Node* pparent = parent->_parent;Node* cur = parent->_right;Node* leftchild = cur->_left;//旋转//. 成为爷爷的右儿子 (如果没有爷爷,则跳过;且说明父是根,更新我成为根)if (pparent) {              //有爷爷if(parent == pparent->_left)pparent->_left = cur;else {pparent->_right = cur;}cur->_parent = pparent; //三叉链维护}else {                      //没有爷爷,父亲是根cur->_parent = nullptr;_root = cur;}//. 父子地位交换parent->_right = leftchild;if (leftchild) {            //三叉链维护leftchild->_parent = parent;}cur->_left = parent;parent->_parent = cur;//旋转 【end】//更新平衡因子cur->_bf = 0;parent->_bf = 0;}//2. 左左void RotateR(Node* parent) {//. 记录爷爷//. 我是父的左儿子//. 记录下我的右子树Node* pparent = parent->_parent;Node* cur = parent->_left;Node* rightChild = cur->_right;//旋转//. 成为爷爷的左儿子 (如果没有爷爷,则跳过;且说明父是根,更新我成为根)if (pparent) {              //有爷爷if (parent == pparent->_left)pparent->_left = cur;else {pparent->_right = cur;}cur->_parent = pparent; //三叉链维护}else {                      //没有爷爷,父亲是根cur->_parent = nullptr;_root = cur;}//. 父子地位交换parent->_left = rightChild;if (rightChild) {            //三叉链维护rightChild->_parent = parent;}cur->_right = parent;parent->_parent = cur;//旋转 【end】//更新平衡因子cur->_bf = 0;parent->_bf = 0;}
//3. 左右void RotateLR(Node* parent) {//我是儿子,但是主角是孙子(新插入结点)//记录下孙子//记录下孙子的平衡因子(特征)//对孙子进行左单旋,再右旋//更新平衡因子Node* cur = parent->_left;Node* grandson = cur->_right;int bf = grandson->_bf;RotateL(cur);RotateR(grandson->_parent);//三种情况if (bf == 0) {parent->_bf = 0;cur->_bf = 0;grandson->_bf = 0;}else if (bf == 1) {parent->_bf = 0;cur->_bf = -1;grandson->_bf = 0;}else if (bf == -1) {parent->_bf = 1;cur->_bf = 0;grandson->_bf = 0;}else {assert(false); //错误检查}}//4. 右左void RotateRL(Node* parent) {//我是儿子(父的右孩子),但是主角是孙子//记录下孙子(我的左孩子)//记录下孙子的平衡因子(特征)//对孙子进行右单旋,再左单旋//更新平衡因子Node* cur = parent->_right;Node* grandson = cur->_left;int bf = grandson->_bf;RotateR(cur); //将孙子的爹,就是我,进行右单旋RotateL(grandson->_parent); //将儿子的新爹进行左单旋//三种情况if (bf == 0) {parent->_bf = 0;cur->_bf = 0;grandson->_bf = 0;}else if (bf == 1) {parent->_bf = -1;cur->_bf = 0;grandson->_bf = 0;}else if (bf == -1) {parent->_bf = 0;cur->_bf = 1;grandson->_bf = 0;}else {assert(false);}}

插入操作实现

    bool Insert(const std::pair<K,V> kv) {//第一个结点做根if (_root == nullptr) {_root = new Node(kv);_size++;return true;}//搜索Node* parent = _root;Node* cur = _root;while (cur) {//大于往右走if (kv.first > cur->_kv.first) {parent = cur;cur = cur->_right;}//小于往左走else if (kv.first < cur->_kv.first) {parent = cur;cur = cur->_left;}//找到了,存在相同的keyelse {return false;}} //循环搜索...//不存在,可以插入cur = new Node(kv);                         //new后,cur值发生改变,之后都不能使用地址进行比较if (cur->_kv.first < parent->_kv.first) { parent->_left = cur;}else {parent->_right = cur;}cur->_parent = parent; //三叉链链上父结点_size++;//调整平衡因子 : 最多到根,根的parent为nullptrwhile (parent) {//更新平衡因子if (cur->_kv.first < parent->_kv.first) {parent->_bf--;}else {parent->_bf++;}//看是否需要调整if (parent->_bf == 1 || parent->_bf == -1) {cur = parent;parent = parent->_parent;}else if(parent->_bf == 0){break; }else if(parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == -2 && cur->_bf == -1) {      //左左RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == 1) {   //右右RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == 1) {  //左右RotateLR(parent);}else if(parent->_bf == 2 && cur->_bf == -1){    //右左RotateRL(parent);}else {                                          //错误检查assert(false);}break;}else {assert(false);}}return true;}

树高度与是否平衡树判断实现

    size_t Hight() {return _Hight(_root);}bool IsBalance() {return _IsBalance(_root);}size_t _Hight(Node* root) {if (root == 0) return 0;                //空size_t leftH = _Hight(root->_left);size_t rightH = _Hight(root->_right);return std::max(leftH, rightH) + 1;     //+1:自己高度为1}bool _IsBalance(Node* root) {if (root == nullptr) return true;int leftH = _Hight(root->_left);int rightH = _Hight(root->_right);int bf = rightH-leftH;return  bf == root->_bf         //平衡因子&& (bf > -2 && bf < 2)      //高度差&& _IsBalance(root->_left)  && _IsBalance(root->_right);}

其他实现

#include<iostream>
#include<string>
#include<cassert>template<class K,class V>
struct AVLTreeNode {//三叉链AVLTreeNode<K,V>* _left;AVLTreeNode* _right;AVLTreeNode* _parent;int _bf; //balance factorstd::pair<K,V> _kv;AVLTreeNode(const std::pair<K,V>& kv):_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0),_kv(kv){}
};template<class K,class V>
class AVLTree {
public:using Node = AVLTreeNode<K, V>;AVLTree():_root(nullptr),_size(0){}public:void InOrder() {_InOrder(_root);std::cout<<std::endl;}private:void _InOrder(Node* root) {if (root == nullptr) {return ;}_InOrder(root->_left);std::cout<<root->_kv.first<<" ";_InOrder(root->_right);}private:Node* _root;size_t _size;
};

插入验证

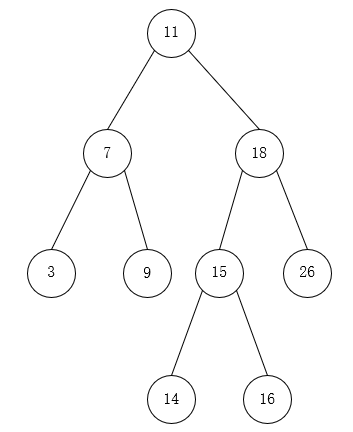
两个数组包含各种旋转情况
每插入都判断是否平衡

int main() {std::cout<<std::boolalpha;//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16,14 };int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };AVLTree<int, int> t;for (int it : a) {t.Insert(std::make_pair(it, it));std::cout << "是否平衡: " << t.IsBalance() << std::endl;}t.InOrder();								//3 7 9 11 14 15 16 18 26
}

/** note* 简称:AVLT* AVL树,也叫高度平衡搜索二叉树* * * * 命名:两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明解决二叉搜索树退化成单支树的方法* -- 所以AVL树以两位俄罗斯数学家的名的开头命名A.V.L.* * 解决问题的方法:* 当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之差的绝对值不超过1* (需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。* * AVL树的定义* 一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树：* $ 它的左右子树都是AVL树* $ 左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)* balance factor(平衡因子/平衡系数) -- AVL树不一定有平衡因子(有些算法没有)* * ? 为什么高度差不能绝对为0? 因为有些情况高度差绝对不可能为0 -- 如偶数个结点时* * 搜索时间复杂度:log2n* * AVL树的性能:* AVL树是一棵绝对平衡的二叉搜索树，其要求每个节点的左右子树高度差的绝对值都不超过1，这* 样可以保证查询时高效的时间复杂度，即log_2 (N)。但是如果要对AVL树做一些结构修改的操* 作，性能非常低下，比如：插入时要维护其绝对平衡，旋转的次数比较多，更差的是在删除时，* 有可能一直要让旋转持续到根的位置。因此：如果需要一种查询高效且有序的数据结构，而且数* 据的个数为静态的(即不会改变)，可以考虑AVL树，但一个结构经常修改，就不太适合。* -- 纯搜索很强* *///AVL树的旋转
/*** 1.右单旋(左左,-2-1):新结点插入在较高左子树的左树 -- (设为该左子树的根为"根",不一定是整棵树的根)* $ 插入前,AVL树是平衡的* 插入后,以根的父节点为根的这棵子树不平衡 -- 设为"父根"* 旋转:将父根取出,根代替父根的位置,而父根取代根的右子树.如果根有右子树,则根的右子树成为父根的左子树* * 解释:>* $ 根位于父根的左子树,将父根和他的右子树一起取出.左子树(根)与父根断链,且链接上父根的父亲的左子树(如果不是整个树的根的话),替代父根称为新的父根 -- 称为上提* $ 由于父根的值是大于根的(搜索树左小右大),所以父根取代的是根的右子树,* $ 若之前根有右子树,因为根的原右子树比根大,而父根又比他的左子树大,即比根的原右子树还大,所以根的原右子树插在父根的左树(父根的左树必为空,因为刚与根断链)* * $ 如果父根是整棵树的根,则调整完后需要更新根节点* 助记:原有位置有子树的,被取代的,按从根开始插入,得到的位置就是新位置* * ? 为什么叫右单旋?  可以理解成右下旋  -- 右边高右边旋* * 2.左单旋(右右+2+1): 和右单旋一样* * $ 单旋：你的右变我的左，我的左变你的右（先断子树后父树）* * * * 3.新结点插入较高左子树的右侧(左右) :* $ 先左单旋再右单旋(先左子树的子(两个绝对值为1的)树旋,后两个父(两个绝对值为2的)旋)* * 4.新结点插入较高右子树的左侧 -- (右左)* $: 先右单旋再左单旋* * * * 注::::::::::::::::::::::::::::::::::::::::::::* $ 在下述例子中,图像只为具象出来写代码,举例用.实际上旋转的多种情况主要是看平衡因子* $ 选出四种旋转方式的例子的图并不代表所有的情况都如图,但这四种方式对应的平衡因子是所有情况* $ 所以算法没有问题,图要多揣摩一下* * * 实际就四种：* 1. /       2. \          3.    /               4.   \*   /            \               \                    /* 右旋         左旋        先左旋后右旋           先右旋后左旋* * * *///模拟实现AVL -- map底层
/*** * * insert插入* 1.三叉链链接到位(链接上插入的结点,新结点也要链接上父亲)* 2.更新平衡因子* $ 如果更新后所有的平衡因子都为-1,0,1其中一个,则不需要调整平衡树* $ 如果更新后有平衡因子的绝对值>1,则需要调整平衡树* 3.调整平衡树* * note:* $ 新增的结点,只会影响到他祖先的这一路径的结点* $ 往上更新爷爷结点取决于parent的高度是否发生变化.变了则往上更新(前提是平衡状态),不变则不再更新.*   parent._bf如果更新后为0,说明结点插在矮树这边,使左右子树平衡,即高度不变*   parent._bf如果更行后为-1或1,说明左子树高或右子树高了,高度变了* $ 如果parent-_bf为2,则需要先处理,不能再继续更新(不再平衡)* */
#include<assert.h>
#include<iostream>
using std::cout;
using std::endl;
using std::cin;
using std::pair;namespace test
{template<class K, class V>struct AVLTreeNode{//三叉链: left right parentAVLTreeNode* _left;AVLTreeNode* _right;AVLTreeNode* _parent;std::pair<K, V> _kv;     //键值对int _bf;            //balance factor -- 平衡因子 :默认规定为右子树高度减去左子树高度AVLTreeNode(const std::pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0){}};template<class K, class V>class AVLTree{public:typedef AVLTreeNode<K, V> node;private:node* _root = nullptr;public:bool insert(const std::pair<K, V>& kv){if (!_root){_root = new node(kv);return true;}node* cur = _root;node* parent = nullptr;while (cur){if (kv.first > cur->_kv.first){parent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new node(kv);if (kv.first>parent->_kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//cur->_bf = 0;//cout << "插入后父亲的平衡因子:>"<<parent->_bf << " ";while (parent){if (cur == parent->_left){--(parent->_bf);//cout << "更新后父亲的平衡因子:>"<<parent->_bf << " ";}else {++(parent->_bf);//cout << "更新后父亲的平衡因子:>" << parent->_bf << " ";}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){parent = parent->_parent;cur = cur->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//if (parent->_bf == 2 && cur->_bf == 1){//cout << "RotateL" << " ";RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){//cout << "RotateR" << " ";RotateR(parent);}else if (parent->_bf == -2 && cur->_bf == 1){//cout << "RotateLR" << " ";RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){//cout << "RotateRL" << " ";RotateRL(parent);}else{cout << " 错误的结点的父 " << parent->_kv.first << " 错误的结点的子 " << cur->_kv.first << " ";assert(false);}break;}else{assert(false);}}//cout << endl;return true;}public:void InOrderTraversal(){_InOrderTraversal(_root);}bool isBalanceTree(){return _isBalanceTree(_root);}int Height(){return _Height(_root);}private:bool _isBalanceTree(node* root){if (!root){return true;}//左右子树高度差的模或bf的模是否小于2int leftH = _Height(root->_left);int rightH = _Height(root->_right);int diff = rightH - leftH;int Hdiff_abs = abs(rightH - leftH);//if (abs(root->_bf) >2 || Hdiff_abs > 2)//{//    cout << "左右子树高度差的模或bf的模大于2,key为:>" << root->_kv.first << endl;//    return false;//}////左右子树的高度差的模是否为bf//if (diff != root->_bf)//{//    cout << "左右子树的高度差的模不等于平衡因子,key为:>"<<root->_kv.first <<" 平衡因子为: "<< root->_bf << endl;//    //return false;//}return abs(root->_bf) < 2&& Hdiff_abs < 2&& diff == root->_bf&& _isBalanceTree(root->_left)&& _isBalanceTree(root->_right);}int _Height(node* root){if (!root){return 0;}int leftH = _Height(root->_left);int rightH = _Height(root->_right);return leftH > rightH ? leftH + 1 : rightH + 1;}void _InOrderTraversal(node* root){if (root == nullptr){return;}_InOrderTraversal(root->_left);cout << "key:> " << root->_kv.first << " " << "bf:> " << root->_bf << endl;_InOrderTraversal(root->_right);}/**左单旋* 设x 为   x           y为   y        z为 z*        1   1             1                 1* * * a,b,c一定是是x,y,z三种情况之一  * * 当c为x情况下,在经过祖先c插入的一定是符合左单旋 -- 右右(右右分别为1,c)* *           p(parent)*       a        sR(subR)*              b(subRL)  c* * 左单旋操作* 1.旋转* $.将b链接到p的左边 然后更新b的_parent , _parent=p(前提是b不为空)* $.将p链接到sR,然后更新p的_parent , _parent=sR* 2.更新根* $.如果是根(pparent==nullptr),则更新_root , _root=subR * $.如果不是根,判断是祖先结点的左还是右,然后再链接上,最后记得更新_parent* 3.更新parent和subR的平衡因子_bf, 旋转后平衡因子都为0 * */void RotateL(node* parent)//左单旋 -- parent是bf为2的结点{node* subR = parent->_right;//sRnode* subRL = subR->_left; //b//1.将b链接到p的右边 然后更新b的parent=p(前提是b不为空)parent->_right = subRL;if (subRL){subRL->_parent = parent;}node* pparent = parent->_parent;//2.将p链接到sR,然后更新p的parent=sRsubR->_left = parent;parent->_parent = subR;//3.更新根if (!pparent){_root = subR;_root->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = subR;}else{pparent->_right = subR;}subR->_parent = pparent;}parent->_bf = subR->_bf = 0;}/*** *            p(parent)*        sL(subL)      c  *       a   b(subLR)  * */void RotateR(node* parent)//右单旋 -- parent是bf为-2的结点{node* subL = parent->_left;//sR    node* subLR = subL->_right; //b//1.将b链接到p的左边 然后更新b的parent=p(前提是b不为空)parent->_left = subLR;if (subLR){subLR->_parent = parent;}node* pparent = parent->_parent;//2.将p链接到sL,然后更新p的parent=sLsubL->_right = parent;parent->_parent = subL;//3.更新根if (parent == _root){_root = subL;_root->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = subL;}else{pparent->_right = subL;}subL->_parent = pparent;}parent->_bf = subL->_bf = 0;}/*** *                       p*       sL                           |d--高度h* |a|--高度h    sLR                   d *  a          b      c--高度h-1       d*  a          b      c                         * * * * * *  $ 在sLR处插入都会引发旋转,因为d矮了*  * 旋转:先左旋,后右旋* * 1.先左旋sL结点,后右旋p结点* 2.更新根* 3.更新平衡因子* $.插在右边,sL为-1* $.插在左边,p为-1* $,如果插入后sLR为0(刚好sLR是新插入的),即h=0，整棵树就3结点，平衡后都是0** * * */void RotateLR(node*parent) //左右{node* subL = parent->_left;node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == 1){parent->_bf = 0;//虽然左旋和右旋已经置零，但是以防万一，安全一点，再次置零subLR->_bf = 0;//虽然左旋和右旋已经置零，但是以防万一，安全一点，再次置零subL->_bf = -1;//必须手动置零}else if (bf == -1){parent->_bf = 1;//必须手动置零subLR->_bf = 0;//虽然左旋和右旋已经置零，但是以防万一，安全一点，再次置零subL->_bf = 0;//虽然左旋和右旋已经置零，但是以防万一，安全一点，再次置零}else if (bf == 0){parent->_bf = 0;subLR->_bf = 0;subL->_bf = 0;}else//以防万一，安全一点{assert(false);}}/*** *                       p*    |a--高度h                  sR                          *     a              sRL                 |d|--高度h  *     a            b      c--高度h-1      d          *                  b      c               d                     * */void RotateRL(node* parent) //右左{node* subR = parent->_right;node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 1) //插在右边,右边平衡,左边不平衡{subR->_bf = 0;parent->_bf = -1;subRL->_bf = 0;}else if (bf == -1) //插在左边,左边平衡,右边不平衡{subR->_bf = 1;parent->_bf = 0;subRL->_bf = 0;}else if (bf == 0){subR->_bf = 0;parent->_bf = 0;subRL->_bf = 0;}else//以防万一，安全一点{assert(false);}}};void test_AVL1(){int arr[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 }; //结点7:左右 结点9:右 结点26:左 结点18:右左 结点15:左右//int arr[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 }; //只有一个右左,结点6test::AVLTree<int, int> t;for (auto i : arr){cout << "i:>" << i << "\t";t.insert(std::make_pair(i,i));cout << endl;}t.InOrderTraversal();cout << "是否为AVL树? " << t.isBalanceTree() << endl;}#include<time.h>void test_AVL2(){srand((size_t)time(0));const size_t N = 5000000;test::AVLTree<int, int> t;for (size_t i = 0; i < N; ++i){size_t x = rand() + i;//size_t x = rand() * i - rand();//cout << "x:>" << x << "\t";t.insert(std::make_pair(x, x));}//cout << t.isBalanceTree()<<endl;cout << "AVLT高度:>" << t.Height() << endl;}
}

结语：感谢相遇